基于模糊集合理论的液压缸故障树分析方法研究

赵海鸣,　熊志宏,　曾　雷,　张　欢

(1.中南大学 机电工程学院,湖南 长沙　410083; 2.中南大学 高性能复杂制造国家重点实验室,湖南 长沙　410083)



基于模糊集合理论的液压缸故障树分析方法研究

赵海鸣1,2,熊志宏1,曾雷1,张欢1

(1.中南大学 机电工程学院,湖南 长沙410083; 2.中南大学 高性能复杂制造国家重点实验室,湖南 长沙410083)

摘要:文章针对汽车起重机液压缸故障,建立了一个比较完整的故障树;针对液压缸故障树分析时存在底事件故障概率获取不足的特点,将模糊集合理论和专家判断法引入故障树分析法(fault tree analysis,FTA)中,使故障树具有处理模糊信息的能力;在对故障树进行传统定性分析的基础上,将底事件发生概率的可靠性数据与通过模糊计算获得的模糊概率相结合进行故障树定量分析。结合某型号汽车起重机实例数据进行分析,估计出了故障树子树顶事件的模糊故障概率及其各底事件的重要度。

关键词:液压缸故障树分析;模糊集合理论;模糊概率;定量分析;重要度

汽车起重机是一种常见的工程机械,液压系统是汽车起重机的重要组成部分,液压系统故障是汽车起重机发生故障的主要原因。液压缸是液压系统中常用的执行部件,经常会出现故障且不易诊断和排除,故对其进行故障诊断非常必要。

故障树分析法(fault tree analysis,FTA)是分析系统安全性和可靠性的有效工具,它先指定系统中一个最不希望发生的状态作为故障分析的目标,即顶事件,然后在一定的环境与工作条件下对系统进行分析,用规定的逻辑符号自上而下地分析导致顶事件发生所有可能的直接原因以及相互间的逻辑关系,并由此逐步深入分析,直到找到事故的基本原因,即故障树的底事件为止。FTA的最终目标是在应用过程中,深入对系统的理解,找出系统的薄弱环节,提高系统的安全性与可靠性[1]。

本文利用FTA,选择液压缸故障为顶事件,建立一个相对完整的液压缸故障的故障树,并结合模糊集合理论对故障树进行定量分析,为维修和故障排除提供一定的依据和方法。

1液压缸故障树建立

本文以汽车起重机的液压缸故障为分析对象,分析中遵循了一定的假设条件:① 底事件只有正常和故障2种状态;② 各底事件彼此相互独立;③ 不存在外界干扰[2]。

结合某公司提供的某型号110 t汽车起重机液压缸故障统计数据,对能够直接观察到的液压缸故障现象进行分类分析,选取“液压缸故障”为顶事件。液压缸故障的主要表现为液压缸动作不正常、漏油和零部件损伤，只要出现其中1个事故,都会导致液压缸故障,因此用逻辑“或”门将它们与顶事件相连。如果出现液压缸漏油故障,可能是由缸头与活塞杆或缸筒之间的密封件失效、油缸焊接缺陷、活塞杆拉伤、连接处接头或螺纹松动等原因造成的,任何一个事件发生,都会使液压缸出现漏油事故,故也用逻辑“或”门连接。由此类似分析,可得到液压缸故障的故障树,如图1所示。

图1　液压缸故障树示意图

故障树中各符号的含义如下:

(1) 顶事件T表示液压缸故障。

(2) 中层事件M。M1表示液压缸动作不正常;M2表示漏油;M3表示零部件损伤;M4表示液压缸无动作;M5表示液压缸动作缓慢,未达到规定值;M6表示爬行;M7表示冲击;M8表示压力不足;M9表示压力达到,仍无动作;M10表示内泄漏严重;M11表示液压缸内部“别劲”。

(3) 底事件x。x1表示缸头与活塞杆或缸筒之间的密封件失效;x2表示油缸焊接缺陷;x3表示油缸有砂眼;x4表示活塞杆拉伤;x5表示连接处接头或螺纹松动;x6表示缸体损伤;x7表示油缸质量问题;x8表示油管质量问题;x9表示装配不良;x10表示操作失误导致电击伤等;x11表示活塞杆、导向套和沟槽等加工质量差;x12表示油缸开裂或断裂;x13表示油缸变形;x14表示油缸支座开裂;x15表示法兰盘脱落或焊缝处开裂;x16表示油缸球头脱落;x17表示导向套脱落;x18表示活塞杆镀层脱落;x19表示其他质量问题;x20表示油缸局部胀大;x21表示缓冲间隙过大;x22表示蓄能器容量不足或充气压力不足;x23表示活塞杆磨损;x24表示活塞杆弯曲;x25表示混入空气;x26表示密封件装配过紧;x27表示活塞杆两端螺母过紧;x28表示缸筒内壁拉伤与磨损;x29表示配合面之间间隙过大;x30表示导向套润滑不良;x31表示缓冲作用失灵;x32表示外载荷过大;x33表示油液未进入油箱;x34表示油液压力未达到规定值;x35表示液压缸结构上的问题;x36表示液压系统引起的故障;x37表示油液被污染;x38表示活塞与活塞杆、缸筒之间的密封件失效;x39表示活塞、活塞杆与缸筒之间同轴度差;x40表示活塞有毛刺、洼点、镀铬层脱落;x41表示活塞拉伤与磨损;x42表示活塞径向断裂;x43表示油温过高,黏度下降;x44表示液压缸装配不良;x45表示配合间隙过小;x46表示缸筒圆度差。

2故障树定性分析

定性分析用于识别故障模式,判明潜在故障,最终指导故障诊断。故障树定性分析主要是找出导致顶事件发生的所有可能的故障模式及其状态组合,即求出故障树的全部最小割集。最小割集是导致故障树顶事件发生的数目不可再少的底事件的组合,它表示引起故障树顶事件发生的一种故障模式[3]。求故障树最小割集的常用方法是先将故障树转化为等效的布尔方程,再利用上行法或下行法求解[4]。这里采用上行法,即依据故障树自下向上进行,最底层的逻辑门用输入事件表示,“或”门和“与”门分别是事件的并和交,一步步往上推,求出顶事件表达式,并用布尔代数运算获得最小割集。

本文将求割集和最小割集按照中层事件M1、M2、M3分为3个过程,而M1又分为M4、M5、M6、M74个过程。以M5为例,用上行法求得:

(1)

由于整个故障树只有单一的“或”门,且在故障树分析中经常处理的是独立的小概率部件失效,所以通常不需要区分相容和不相容的“或”门。在14个底事件中只要有1个发生,就能导致事件M5发生。所以,这14个底事件中每个都是一个一阶最小割集,即M5的全部最小割集为:{x20}、{x21}、{x22}、{x28}、{x29}、{x38}、{x39}、{x40}、{x41}、{x42}、{x43}、{x44}、{x45} 、{x46}。

3故障树定量分析

传统的FTA存在以下局限性:① 底事件故障概率需要精确已知;② 事件之间的联系需要精确已知;③ 故障发生的严重程度无法描述。这使得在故障树的建立和定量分析时面临许多问题,限制了FTA的应用。而模糊理论具有处理模糊和不精确信息的优点,将FTA与模糊理论相结合,可以弥补传统FTA的不足[5-6]。

本文分析是以NK-160型汽车起重机液压系统测试维修记录[7]结合专家知识为背景,针对液压缸故障各底事件发生概率获取情况不足的现状,采用模糊理论获得现在未能获取的底事件发生的模糊概率,根据模糊数归一化方法,结合实际经验和资料数据,得到各底事件发生的概率评价及其归一化结果,然后再对其进行故障树定量分析。

由于本故障树比较复杂,底事件较多,以下的定量分析都是以子树M5为例,并作为其他子树和整个故障树定量分析的参照。在子树M5中,事件M5可以看作是子树的顶事件。

3.1模糊数介绍

模糊故障树分析方法是将模糊集合理论和可能性理论引入到故障树分析中,将底事件发生的概率描述为模糊数和模糊可能性,通过模糊数的运算来估计底事件的故障概率和底事件的重要度[8]。专家判断法是确定底事件发生模糊概率的常用方法之一。根据自己的经验，专家难以对事件发生的概率给出精确的估算值,只能倾向于采用如“低”、“高”等语言值来描述[1]。本文使用的语言值集合为{很低,低,较低,中等,较高,高,很高}={VL,L,FL,M,FH,H,VH},表示故障模糊概率的语言评价。选用的代表语言值的模糊数如图2所示[9]。

图2　代表语言值的模糊数

因为语言值具有模糊性,本文采用模糊集理论处理这些不确定信息。由于梯形模糊数为线性隶属函数,直观且代数运算较为简单,因此,本文采用梯形模糊数来进行研究。

3.2底事件发生概率的确定

以M5为顶事件的子故障树,经定性分析,得其最小割集为:{x20}、{x21}、{x22}、{x28}、{x37}、{x38}、{x39}、{x40}、{x41}、{x42}、{x43} 、{x44}、{x45}、{x46}。根据NK-160型汽车起重机液压系统测试维修记录,事件M5的底事件概率已知，见表1所列。

表1　M5已知底事件概率　%

由于信息资料不足,底事件概率未知的最小割集为:{x20}、{x22}、{x40}、{x42}、{x46}。

(1) 为确定这些未知的底事件概率,选择了6位专家,对这些底事件的可能性用语言值做主观判断。这6位专家对各未知概率的底事件评估意见见表2所列。

表2　底事件评估意见

(2) 把专家评估意见语言值转化为模糊数。根据图2语言值的模糊数表现形式,给出其隶属度函数表达式分别为:

(2)

(3)

(4)

(5)

对这6位专家的评估意见进行综合处理,通常是选用模糊集的α截集方法和平均算法来组合不同的专家意见[10]。设(2)～(5)式的α截集分别为:VLα=[v1,v2],Lα=[l1,l2],FLα=[f1,f2],Mα=[m1,m2]。其中v1、v2、l1、l2、f1、f2、m1和m2分别为(2)～(5)式α截集上限和下限。以fVL(x)为例,令α=(0.2-x)/0.1,则v2=0.2-0.1α,v1=0;同理可得:l1=0.1α+0.1,l2=0.3-0.1α,f1=0.1α+0.2,f2=0.5-0.1α,m1=0.1α+0.4,m2=0.6-0.1α。

对底事件x20,由表2可知,专家组的评估意见为:很低、低、低、低、低、低。在α截集下,6位专家意见的总的模糊数z为:

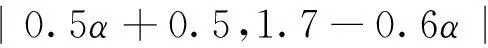
(6)

(6)式的平均模糊数Wx20为:

|0.083 33α+0.083 33,0.283 3-0.1α|。

(3) 把模糊数转化为模糊可能性值。因为一个模糊数可能代表不同的隶属度函数的许多实数,在故障树分析中很难把最终得到的结果进行分析比较,所以必须把模糊数转化为一个清晰的值,即模糊可能性值(FPS)。FPS代表的是专家对某一事件发生可能性的信任度。

基于文献[11]提出的左、右模糊排序法,把模糊数转化为FPS。该方法定义最大模糊集和最小模糊集为:

则模糊数Wx20的左、右模糊可能性值分别为:

因此,模糊数Wx11的模糊可能性值为:

1-FPSL(Wx20)|/2=0.205 7。

(4) 把FPS转化为模糊失效率(FFR)。故障树底事件发生的概率一些是已知的，另一些则是由模糊集理论和专家判断法相结合得到的。为确保已知失效概率和模糊失效概率之间的一致性,需把FPS转化为模糊失效率FFR[12],即

(7)

其中,Θ为模糊减法运算;Π为模糊乘法运算。

根据模糊数归一化方法,结合给出的确定底事件概率和所求得的模糊数及失效率,得到该故障子树的各底事件发生概率评价结果和归一化结果，见表3所列。

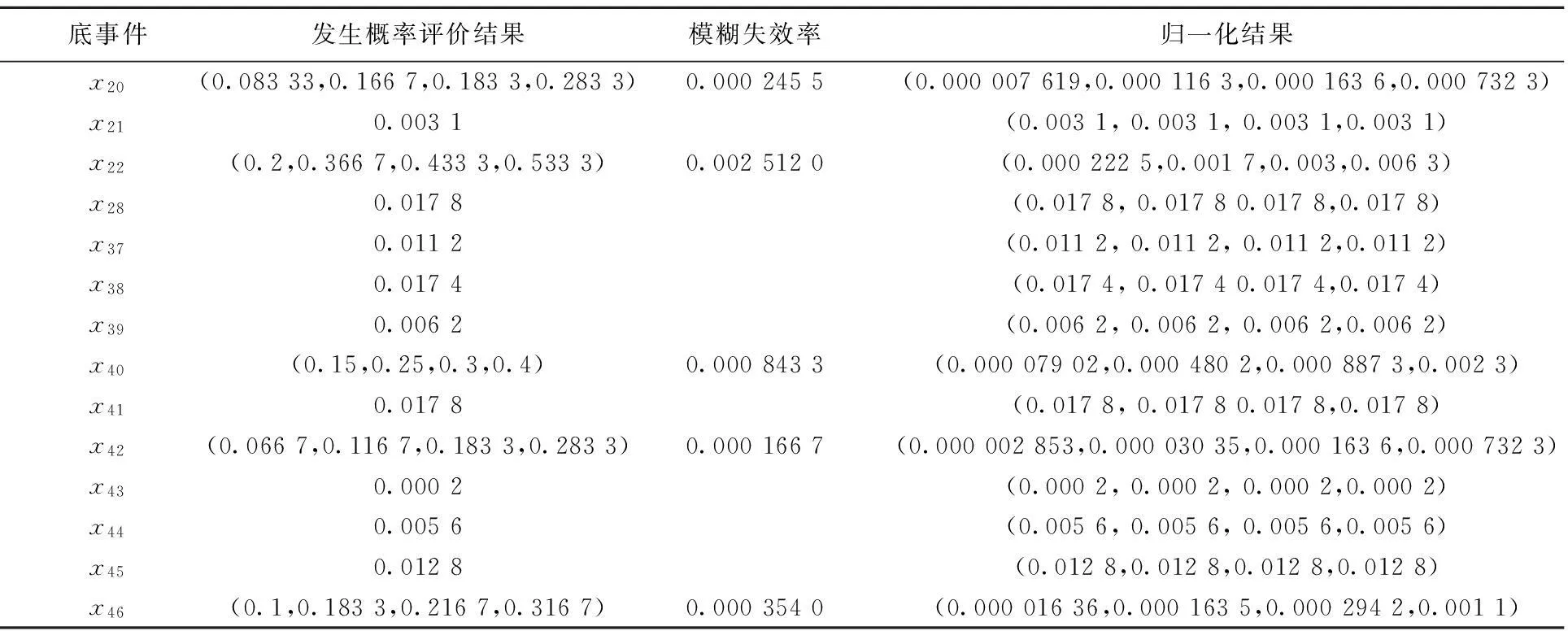
表3　底事件发生概率及归一化结果

基于故障树分析基本假设条件,根据梯形模糊数运算法则中“或”门算子可得到相应的顶事件发生概率的模糊数为:

(0.088 887,0.090 856,0.092 692,0.098 728)

(8)

由(8)式可知,该故障树子树的顶事件即“液压缸动作缓慢,速度未达到规定值”的发生概率大约在0.090 856~0.092 692之间。更确切地,发生概率约在8.888 7%~9.872 8%之间,但顶事件发生的概率在9.085 6%~9.269 2%之间的可能性最大,其隶属度为1。这种顶事件发生概率的模糊性是由底事件发生概率的模糊性所决定的,保留这种模糊性的描述更能反映事件的本质。

3.3底事件概率重要度分析

各底事件的发生概率对系统故障的影响程度,可用底事件的概率重要度表示。一般地,当已知各底事件发生概率时,可用顶事件的发生概率对某个底事件的发生概率的偏导数表示这个底事件的概率重要度。设P(t)为顶事件的发生概率,Pxi(t)为底事件xi的发生概率,Ixi为底事件xi的概率重要度,即

(9)

(10)

当故障树底事件和顶事件用模糊数描述时,求底事件概率重要度一般有Hideo Tanaka模糊重要度法、重心法[13]和中值法等,但实际系统比较复杂时,这些方法计算会比较困难。按照底事件的重要度排序,对系统的设计、预防系统故障十分必要。鉴于本文讨论的概率模糊数均为梯形模糊数，使用表3中计算得到的模糊失效率及已知的底事件失效概率,利用(9)式和(10)式来近似计算底事件概率重要度,得到的结果见表4所列。

表4　底事件概率重要度

由表4中重要度大小可知,各底事件概率重要度排序为Ix28=Ix41>Ix38>Ix45>Ix37>Ix39>Ix44>Ix21>Ix22>Ix40>Ix46>Ix20>Ix43>Ix42。其中,底事件x28、x41、x38、x45等对顶事件影响较大。为了提高系统的可靠度,应先从提高具有较大概率重要度的底事件入手。同时,当系统发生故障时,也可根据底事件概率重要度的大小顺序排查故障原因。

由计算分析可知,在M5下面的中层事件M10内泄漏严重故障中概率重要度靠前的5个底事年排序为Ix28=Ix41>Ix38>Ix37>Ix39。这与某公司提供的某型号110 t汽车起重机液压缸内泄漏故障的统计概率排序基本符合,验证了上述方法在液压缸故障分析中的基本可行性。该公司提供的某型110 t汽车起重机液压缸内泄漏故障统计概率见表5所列。

表5　内泄漏故障统计概率　%

通过对液压缸进行模糊故障树分析,可得到顶事件发生概率和关键底事件对顶事件发生的影响程度,既可以评价液压缸的可靠性,也为设计和维护过程中重要环节的改进和保护提供依据。上述方法可应用于整个液压缸的故障树中,基本可以分析出液压缸故障的原因,为维修和故障排除提供依据和方法。

4结束语

本文针对汽车起重机液压缸故障,建立了一个比较完整的故障树,把模糊集合理论引入故障树分析中,使用梯形模糊数、语言值及精确概率值描述底事件的发生概率,得出子树M5顶事件发生概率大约在8.888 7%~9.872 8%之间,并给出了底事件的重要度排序，为液压缸针对子树M5故障的设计、维修和故障排除提供了一定的依据和方法。同时,还可以把此方法应用到整个液压缸故障树分析中。

[参考文献]

[1]魏臻,许崇.基于FTA的矿井提升监控系统可靠性分析[J].合肥工业大学学报:自然科学版,2013,36(8):919-922.

[2]李河清,谭青,林光霞.叉车液压系统起升液压缸无力的故障树分析[J].机床与液压,2008,36(2):199-201.

[3]隆建波.故障树理论在混凝土泵车泵送液压系统故障诊断与维护中的应用[D].长沙:长沙理工大学,2013.

[4]姚竹亭, 潘宏侠, 吴立新,等. 故障树法在车辆控制系统CPU板故障诊断中的应用[J]. 合肥工业大学学报:自然科学版, 2009, 32(9):1317-1319.

[5]Song H, Zhang H Y, Chan C W. Fuzzy fault tree analysis based on T-S model with application to INS/GPS navigation system[J]. Soft Computing, 2009, 13(1):31-40.

[6]姚成玉,赵静一.基于T-S模型的液压系统模糊故障树分析方法研究[J].中国机械工程,2009,20(16):1913-1917.

[7]刘希亮,陈小虎.汽车起重机液压缸爬行的故障树研究[J].机械,2008,35(10):60-62.

[8]朱震江,杨晓翔.城市埋地燃气管道模糊故障树分析[J].合肥工业大学学报:自然科学版,2007,30(12):1686-1690.

[9]武庄,石柱,何新贵.基于模糊集合论的故障树分析方法及其应用[J].系统工程与电子技术,2000,22(9):72-75.

[10]Lin C T, Wang M J J. Hybrid fault tree analysis using fuzzy sets[J]. Reliability Engineering and System Safety, 1997, 58(3):205-213.

[11]Chen S J J, Hwang C L, Beckmann M J, et al. Fuzzy multiple attribute decision making methods and applications[M].Berlin：Springer-Verlag，1990：372-376.

[12]Onisawa T. An approach to human reliability in man-machine systems using error possibility[J]. Fuzzy Sets and Systems, 1988, 27(2):87-103.

[13]李彦峰.模糊故障树分析方法及其在复杂可靠性分析中的应用研究[D].成都:电子科技大学,2009.

(责任编辑胡亚敏)

Research on fault tree analysis method for hydraulic cylinder based on fuzzy set theory

ZHAO Hai-ming1,2,XIONG Zhi-hong1,ZENG Lei1,ZHANG Huan1

(1.College of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China; 2.State Key Laboratory of High Performance Complex Manufacturing, Central South University, Changsha 410083, China)

Abstract:According to the hydraulic cylinder fault of the truck crane, a relatively complete fault tree is established. Aiming at the insufficient information of fault probabilities of the bottom events during fault tree analysis(FTA) of hydraulic cylinder, the fuzzy set theory and expert judgment method are introduced into FTA method, making the FTA capable of handling the fuzzy information. On the basis of the traditional qualitative FTA, the reliability data of the probability of the bottom events and the fuzzy probability obtained by fuzzy calculation are combined for the quantitative FTA. The instance data of a certain type of truck crane are illustrated, and the fuzzy fault probability of top event of sub-tree and its importance degrees of bottom events are achieved.

Key words:fault tree analysis(FTA) of hydraulic cylinder; fuzzy set theory; fuzzy probability; quantitative analysis; importance degree

中图分类号:TH137.51

文献标识码：A

文章编号：1003-5060(2016)02-0150-06

Doi:10.3969/j.issn.1003-5060.2016.02.002

作者简介：赵海鸣(1966-)，男，湖南邵阳人，中南大学副教授，硕士生导师.

基金项目：国家高技术研究发展计划(863计划)资助项目(2013AA040203)

收稿日期：2014-12-24；修回日期：2015-01-19