基于CKF和R-T-S平滑的车载SINS/OD动基座对准方案*
黄湘远,汤霞清,武 萌
(装甲兵工程学院控制工程系,北京 100072)
2016160
基于CKF和R-T-S平滑的车载SINS/OD动基座对准方案*
黄湘远,汤霞清,武 萌
(装甲兵工程学院控制工程系,北京 100072)
为提高车载捷联惯导/里程计组合系统的动基座对准精度、速度和位置导航精度,提出了“容积卡尔曼滤波(CKF)非线性对准+非线性R-T-S平滑+再次Kalman滤波线性对准”的方案,即首先应用CKF进行非线性对准,对准结果方位对准精度一般、位置误差较大;接着利用R-T-S平滑获得初始时刻高精度对准结果,此时非线性误差模型退化为线性模型;最后再进行Kalman滤波线性对准而获得高精度方位对准精度和位置导航。该方案无需长时间的粗对准,最终能获得高精度的结果。实车试验验证了该方案的有效性。
捷联惯导/里程计组合系统;容积卡尔曼滤波;非线性R-T-S平滑;卡尔曼滤波
前言
基于捷联惯导(strapdown inertial navigation system, SINS)/里程计(odometer, OD)的组合导航系统已广泛应用于陆用导航[1-2]。系统正常工作之前必须进行初始对准,对准分为粗对准和精对准两个过程。
由于里程计不能提供绝对的速度信息和位置信息,导致动基座对准中无法进行高精度定位,对准结束后载体位置误差可能较大。文献[3]中提出一种惯性系对准方案,忽略对准过程中的位置变化,长时间后位置误差较大。文献[4]和文献[5]中以惯性系对准方案完成粗对准,基于小角度误差模型利用线性滤波完成精对准,获得较高精度。上述文献认为60s内能够获得小失准角对准结果,均没有考虑粗对准过程中的位置误差。在履带式装甲车辆这一特殊载体中,经过多次实验表明,运动过程中至少需5min左右才能获得小失准角结果,此时该方案带来较大的位置误差。CKF是一种优秀的非线性滤波器[6-7],在多个领域获得了大量的应用。本文中推导了采用大失准角SINS/OD非线性误差模型,利用CKF进行非线性对准,对准结束后方位精度较高,位置精度一般,但高于惯性系对准方案的位置精度。
为了保证对准结束后位置精度,文献[8]中设计了逆向导航算法,进行再次导航;为了加快对准速度,文献[9]中引入了循环解算思路,文献[10]中提出了严格逆向过程的罗经回溯对准方法;文献[11]中提出基于状态估计的卡尔曼滤波逆向导航算法。逆向思路的导航处理或状态估计可解决对准速度和位置导航的问题。非线性对准的逆向处理可通过非线性R-T-S平滑来实现[12-13],无需进行逆向导航解算。
本文中利用CKF进行非线性对准,对准结束时利用非线性R-T-S平滑迭代至初始时刻,得到载体初始姿态。利用存储数据再次进行导航解算,利用Kalman滤波进行线性对准至结束时刻。最后进行了实车实验,结果表明经过再次对准之后,方位精度和位置精度都得到了较大的提高,该方案同时实现了高精度对准和位置导航。
1 SINS/OD非线性对准模型
1.1 SINS非线性误差
记地心惯性坐标系为i系;地球系为e系;导航系n系为东北天(o-ENU)坐标系;计算平台系为p系;载体系为b系;里程计坐标系m系为右前上坐标系。
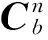
φ=[φE,φN,φU]T
n系下载体速度vn=[vE,vN,vU]T
速度误差δvn=[δvE,δvN,δvU]T
载体纬度L、经度λ和高度h的位置误差为
δp=[δL,δλ,δh]T
大失准角下,基于欧拉角误差的非线性姿态、速度和位置误差的微分方程[14]为
(1)
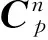
该模型要求纬度误差δL为小量。非线性对准过程中,为了保证δL为小量,可通过位置、速度间歇性闭环反馈来抑制速度和位置误差的快速发散。
1.2 OD误差
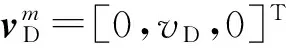
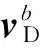
(2)
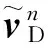
(3)
式中ωD为里程计随机量测噪声。
当失准角φ=[φE,φN,φU]T为大角度时,里程计速度在计算平台系p系的实际输出为
(4)
1.3 SINS/OD动基座非线性对准系统
对准过程中,需对陀螺、加速度计和里程计误差进行估计和补偿。由于对准时间较短,可将陀螺零偏εb、加速度计零偏b和里程计误差ξD视作随机常值,即
(5)
非线性对准系统的状态由姿态误差φ、速度误差δvn、位置误差δp、陀螺零漂εb、加速度计零偏b和里程计误差ξD构成,即

(6)

(7)
由式(1)、式(5)和式(7)构成SINS/OD的非线性对准系统:
(8)
式中:f(x)和h(x)为非线性函数;w为系统噪声;v为测量噪声。w和v互相独立,且w~N(w;0,Q),v~N(v;0,R),Q和R为噪声方差矩阵。
当姿态误差φ为小角度时,非线性系统退化为线性系统,可以用Kalman滤波完成对准。
2 CKF及R-T-S平滑
2.1 CKF算法
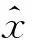
为了提高CKF的滤波精度,文献[7]中提出了5阶CKF,滤波精度达到5阶。为了避免滤波过程中由于协方差矩阵Pk失去正定性导致滤波精度下降,提高算法的数值稳定性,使用协方差矩阵奇异值分解(SVD)代替Cholesky分解,算法实现如下。
(1) 时间更新
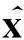
(9)
b.初始采样
(10)
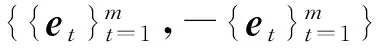
[0,0,…,1]T}T
c.状态传播
(11)
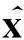
(12)
(2) 量测更新
a.SVD分解Pk|k-1

(13)
b.重采样
(14)
c.观测传播
η0=h(y0);ηi=h(yi);ηj=h(yj)
(15)
(16)
e.利用高斯滤波框架完成非线性滤波
(17)
2.2 基于CKF的非线性对准仿真
假设陀螺常值漂移0.02°/h,随机漂移为0.01°/h,加速度计常值零偏为1×10-4g,随机零偏为5×10-5g。里程计安装失准角δαψ=0.5°,δαγ=0.5°,标定系数误差δKD=0.02。车辆初始位置纬度L=39.84°,经度λ=116.12°。设置车辆运动过程如下:车辆静止;北向1m/s2匀加速10s;匀速运动200s;2°/s左转弯90°;匀速运动200s;2°/s右转弯90°;匀速运动200s。
分别设置初始失准角1[0.1°,0.1°,0.5°]、失准角2[1°,1°,10°]和失准角3[2°,2°,30°],进行非线性对准仿真,时间700s。由于水平对准速度快,精度高,因此只分析方位对准情况。图1给出了方位对准结果,图2给出了对准过程中的水平位置误差。
图1表明失准角1和2方位对准精度较高,失准角3对准精度相对较差。图2表明小失准角下位置误差较小,大失准角下位置误差较大。因为里程计测量的是m系下车辆前向速度,由m系到n系的转换过程中耦合了姿态误差,造成n系下速度参考信息vn误差较大,导致对准开始时刻的位置误差迅速增大,对准一段时间后各项误差逐步得到估计,位置误差逐步减小。由于SINS/OD组合系统的位置误差是发散的,随着时间的继续增长,位置误差将缓慢增大。相对于惯性系对准过程中忽略位置变化的处理方法而言,此位置误差依然相对较小。由于多种误差的互相耦合导致大失准角下陀螺零漂εb、加速度计零偏b和里程计误差ξD估计精度相对较差。
大失准角对准结束时,若在此对准结果的基础上进行SINS/OD组合导航,带来较大的初始位置误差,该误差在后续组合导航中无法进行修正。应急情况或位置精度相对较低的情况下,可直接使用此对准结果,组合导航过程中一旦有位置参考信息时可进行校正。当计算速度较快或有多个处理器时,为了减小组合导航的位置误差,可借用数据存储和循环解算的思想,利用逆向导航或状态平滑对导航信息进行再处理。
2.3 非线性R-T-S平滑
非线性平滑分为R-T-S平滑[15]和TF平滑[16]两种,前者计算量较小,原理简单,应用较为广泛。非线性R-T-S平滑在前向非线性滤波的基础上进行后向递推,获得此前任意时刻状态估计,精度高于滤波。估计过程分为前向滤波和后向递推两部分。
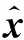
第二部分:后向递推,按照k=N,N-1,…,1的顺序进行逆向递推,即
(18)
经过后向递推后,可获得各时刻的状态平滑估计。图3给出了失准角3方位对准的平滑估计结果,可以看出整个平滑过程中方位失准角为小角度。
3 动基座对准实验
3.1 对准算法设置
(1) 粗对准
非线性对准能够完成大失准角下初始对准。为了在较短的时间里获得较好的估计效果,需对初始方位失准角进行一定的限制。车辆起动或缓慢直线行驶的情况下,采集10s左右的数据,进行惯性系粗对准,获得惯导初始姿态。
(2) 非线性对准
车辆开始行驶,利用CKF进行SINS/OD非线性对准,对准过程中存储相关数据。车辆行驶一段时间后完成非线性对准。
(3) 非线性R-T-S平滑
将存储的前向滤波数据非线性R-T-S平滑至初始时刻,进行姿态修正,获得初始时刻的惯导姿态。
(4) 再次对准
基于存储的惯导数据和里程计数据,进行SINS/OD线性对准至对准结束时刻。
3.2 实验验证
实验室将某型光纤陀螺捷联惯导系统安装在某车辆上,使用车辆自身的里程计信号。光纤陀螺的零偏稳定性不超过0.02°/h,加速度计的偏值重复性小于5×10-5g。首先对SINS和OD的安装偏差角、里程计标定系数进行初始标定。
车辆行驶过程中使用高精度BD2导航芯片进行实时速度、位置测量。由于车辆行驶过程中无法获得准确姿态,姿态参考值由静基座对准后转SINS/BD2组合导航提供。
为了验证非线性对准的有效性,对准初始时刻在参考姿态的姿态上设置失准角φ=[2°,2°,30°],对准时间900s。共进行了5组试验,方位对准结果及位置误差如表1~表3所示。表中:ψ1,λ1和L1为首次非线性对准的方位角、经度和纬度;ψ2,λ2和L2为再次线性对准的结果;ψ,λ和L为参考值。
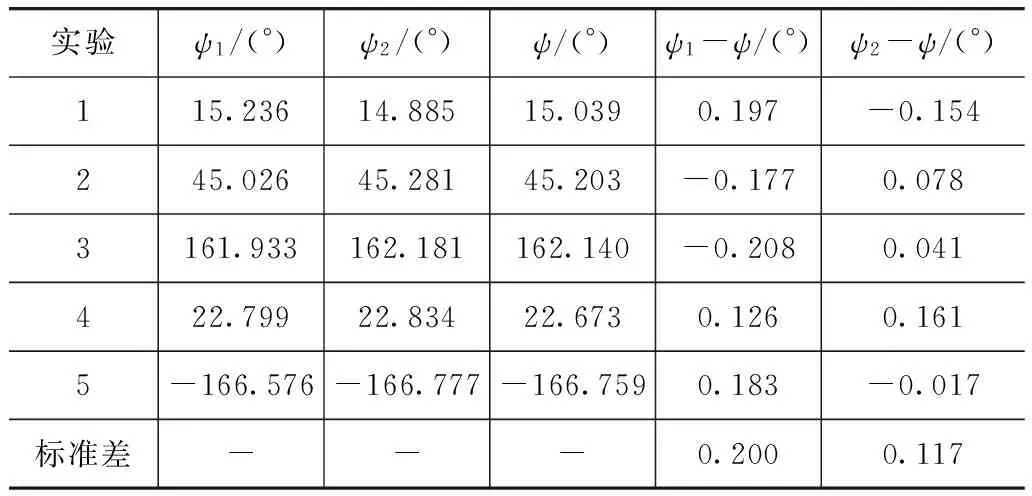
表1 方位对准结果
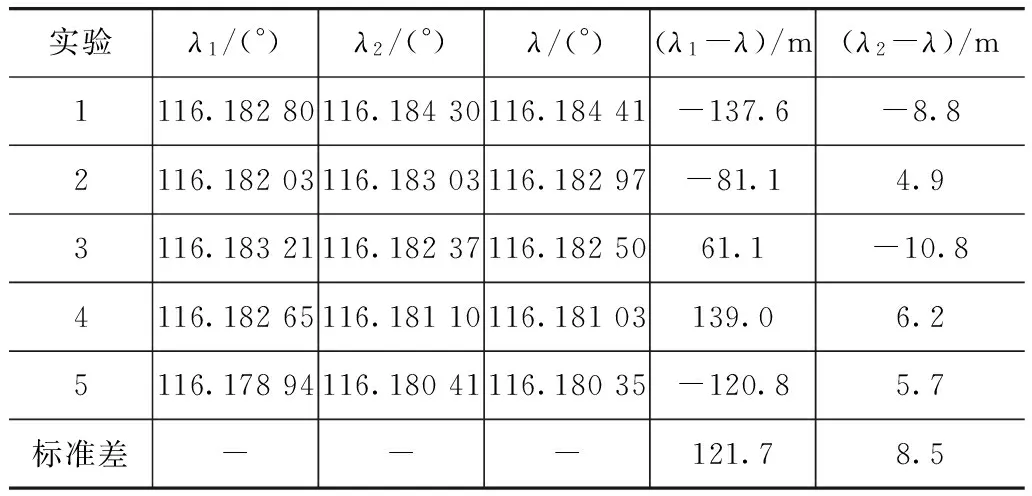
表2 对准结束时的经度误差

表3 对准结束时的纬度误差
非线性对准结束后,方位精度0.200°,经度误差121.7m,纬度误差68.3m,方位角和位置误差较大,其中位置误差对后续组合导航影响更大。尽管如此,对准过程中能够提供相当精度的位置导航,这是惯性系粗对准中较难做到的。经过R-T-S平滑和再次线性对准后,方位精度提高到0.117°,经度误差8.5m,纬度误差11.3m,对准精度和位置精度大幅提高。再次对准大大减小了后续SINS/OD组合导航的初始位置误差和初始姿态误差,从而提高组合导航的精度。
4 结论
为了同时实现SINS/OD动基座对准和位置导航,本文中设计了“非线性对准+非线性后向平滑+再次线性对准”的动基座对准方案。该方案非线性对准在对准结束时能使方位误差为小角度,对准过程中能够提供一定精度的位置导航,经过“平滑+再次对准”的离线操作能够同时提高对准结束时刻的姿态和位置精度。
该对准方案为离线方案,实际应用中需使用实时方案,实时方案还需进一步研究。
[1] WU Yuanxin, WU Meiping, HU Xiaoping, et al. Self-calibration for land navigation using inertial sensors and odometer: observability analysis[C]. AIAA Conference of Guidance, Navigation and Control,2009:1-10.
[2] 朱立彬,王玮.车辆导航系统中里程计标度因数的自标定[J].汽车工程,2013,35(5):472-476.
[3] 严恭敏,秦永元,卫育新,等.一种适用于SINS动基座初始对准的新算法[J].系统工程与电子技术,2009,31(3):634-637.
[4] 赵小明,赵帅,郭永刚,等.基于强跟踪滤波的车载行进间对准[J].中国惯性技术学报,2015,23(2):141-144.
[5] 肖煊,王清哲,付梦印,等.里程计辅助陆用惯导行进间对准方法[J].中国惯性技术学报,2012,20(2):140-145.
[6] ARASARATNAM I, HAYKIN S. Cubature kalman filters[J]. IEEE Transactions on Automatic Control,2009,54(6):1254-1269.
[7] JIA B, XIN M, CHENG Y. High-degree cubature Kalman filter[J]. Automatica,2013,49:510-518.
[8] 严恭敏,严卫生,徐德民.逆向导航算法及其在捷联罗经动基座初始对准中的应用[C].第27届中国控制会议论文集,北京:北京航空航天大学出版社,2008:724-729.
[9] LI Wanli, WU Wenqi, WANG Jinling, et al. A novel backtracking navigation scheme for autonomous underwater vehicles[J]. Measurement,2014,47:496-504.
[10] 李京书,许江宁,何泓洋,等.严格逆向过程的罗经回溯对准方法[J].系统工程与电子技术,2014,36(2):348-353.
[11] GAO Wei, BEN Yueyang, ZHANG Xin, et al. Rapid fine strapdown INS alignment method under marine mooring condition[J]. IEEE Transactions on Aerospace and Electronic System,2011,47(4):2887-2896.
[12] GADSDEN S A, AL-SHABI M, ARASARATNAM I, et al. Combined cubature Kalman and smooth variable structure filtering: a robust nonlinear estimation strategy[J]. Signal Process,2014,96:290-299.
[13] JIA B, XIN M. Rauch-Tung-Striebel high-degree cubature Kalman smoother[C]. American Control Conference,2013:2472-2477.
[14] 严恭敏,严卫生,徐德民.基于欧拉平台误差角的SINS非线性误差模型研究[J].西北工业大学学报,2009,27(4):511-516.
[15] WANG X X, PAN Q, LIANG Y, et al. Application of unscented transformation for nonlinear state smoothing[J]. Acta Automatica Sinica,2012,38(7):1107-1112.
[16] MA Yanhai, FANG Jiancheng, LI Jianli. Accurate estimation of lever arm in SINS/GPS integration by smoothing methods[J]. Measurement,2014,48:119-127.
Moving Base Alignment Scheme for On-board SINS/OD CombinationBased on CKF and R-T-S Smoothing
Huang Xiangyuan, Tang Xiaqing & Wu Meng
DepartmentofControlEngineering,AcademyofArmoredForceEngineering,Beijing100072
In order to improve the alignment accuracy and speed and the accuracy of position navigation of moving base in a strapdown inertial navigation system/odometer (SINS/OD) combination, a scheme of “nonlinear alignment by cubature Kalman filter (CKF) + nonlinear Rauch-Tung-Striebel (R-T-S) smoothing + linear realignment by Kalman filter” is proposed. Specifically, a nonlinear alignment is conducted by CKF first with a result of ordinary azimuth alignment accuracy and a relatively significant position error, then a nonlinear R-T-S smoothing is performed to obtain a high accuracy alignment result at initial moment with the nonlinear error model degenerated to linear model, and finally a linear realignment is carried out by Kalmann filter to obtain high accuracy azimuth alignment and position navigation. The scheme can obtain a high accuracy result without time-consuming coarse alignment, and the real vehicle test verifies the effectiveness of the scheme proposed.
strapdown inertial navigation system/odometer combination; cubature Kalman filter; nonlinear Rauch-Tung-Striebel smoothing; Kalman filter
*军队计划项目资助。
原稿收到日期为2015年7月3日。

