行为保险学系列(一)什么是对的保险决策？——理性保险决策理论及其由来（上）

郭振华　上海对外经贸大学金融学院



行为保险学系列(一)什么是对的保险决策？——理性保险决策理论及其由来（上）

郭振华上海对外经贸大学金融学院

本文受国家自然科学基金面上项目（71173144）的资助。

郭振华，上海对外经贸大学金融学院保险系主任、副教授，兼任中国保险学会理事、上海保险学会理事。长期讲授《保险学》《保险公司经营管理》等课程，主持完成国家自然科学基金、教育部社科基金、上海社科基金项目各一项。

引言：保险市场异象呼唤“行为保险学”

消费者在是否购买保险（这里主要指承保小概率风险的保障性保险，车险、医疗险和投资险除外）的决策上疑虑重重，保险销售被认为是难度最大的销售工作。同时，高考是否填报保险专业、保险专业毕业生是否到保险业工作也一直令学生们非常纠结，甚至不少保险公司高管也说保险业令人纠结。实际上，这些疑虑和纠结的主要根源是，“保险对多数人来说是一种弱需求产品”，这使得保险销售成为一项极具挑战性的工作。但是，对追求规模增长的保险公司来说，销售越难就越需要大规模和强有力的销售队伍，消费者由此承受了较大的被销售压力，一些消费者开始对保险心存警惕甚至将保险污名化。

经典的经济学理论以“理性人追求效用最大化”为基本假设，证明了在面临风险时，购买保险通常会提升自己的效用水平，论证了理性人会选择购买保险产品，这里称之为“对的保险决策”。

可是在现实世界中，人们往往并不按照经典经济学理论行事，多数人不会主动购买保险。而且，出险概率越低，购买意愿越低。对于小概率风险，即便购买了短期保险，如一年期家庭财产保险，也可能放弃续保。在科特勒著的《市场营销学》中，科特勒将人寿保险归类为“非渴求商品”，非渴求商品的特点是“消费者购买频率低，对产品的知晓度低，即便知晓也没什么兴趣或唯恐避之不及，卖方需要利用激进的广告和强力的人员分销”。

经典经济学和市场营销学在打架，但大家都能明显看出，市场营销学更接近市场，更贴切地描述了真实的保险市场行为。经济学的优势在于用了远比市场营销学要少的假设构建了精妙优美的理论体系，但少不了与市场脱节。近几十年，心理学、生物学、脑科学与经济学逐渐融合发展出了更贴近市场的行为经济学，用以解释纷繁的市场行为，但对保险交易行为尚缺乏系统的行为经济学解释。

在国家自然科学基金的资助下，笔者在该领域做了多年的探索，在前人研究的基础上，借助近几十年来兴起的心理学、生物学、脑科学和行为经济学等理论，逐步形成了一些比较系统的理论，可以用来解释如上保险业存在的不符合经典经济学理论的奇异现象，称为“行为保险学”。

一、概率的由来

早在古代，人们就已经开始玩掷骰子等靠运气决定胜负的赌博或游戏了，但直到17世纪，不管是数学家还是普通百姓，都不知道如何正式地描述和量化不确定事件。例如，掷一枚有6个面的骰子，虽然事前不知道骰子落地后哪一面朝上，但我们现在都知道任意点（1、2、3、4、5或6点）朝上的概率均为1/6。但是，在启蒙运动之前，这并非人尽皆知，概率论这一数学分支一直要等到17世纪后期才由法国数学家布莱士·帕斯卡（Blaise Pascal）发展出来。

（一）赌金分配问题的提出

布莱士·帕斯卡（Blaise Pascal）于公元1623年出生在法国的一个中上层家庭，才华出众，16岁时就发表了《论圆锥曲线》的论文，令笛卡尔大加赞赏，1653年提出了我们中学学过的“帕斯卡定律”，并利用这一原理制成了注射器和水压机。1653年9月，帕斯卡受邀同几位绅士结伴旅行，他们分别是罗尼兹（Roannez）公爵（帕斯卡的资助人）、梅雷（Mere）爵士和明顿（Minton）绅士。旅途中，梅雷爵士向帕斯卡提出了一个赌金分配问题：“梅雷爵士和罗尼兹公爵两人采用连续掷硬币的方式来赌博，每人的赌注是50个金路易。如果先有4次正面朝上，则梅雷爵士赢得全部赌注100个金路易；如果先有4次反面朝上，则罗尼兹公爵赢得全部赌注100个金路易。但是连续抛5次硬币之后由于突发事件，游戏被迫中断了，此时出现了2次反面、3次正面。那么，此时应该怎样分配这100个金路易呢？”

尽管当时科学界尚未发明概率论，但帕斯卡想到的解决思路与我们现在一致，即应该按照每个参与者在之后的抛硬币中获胜的可能性大小来分配赌金。问题是，怎样才能知道每个参与者在之后的抛硬币中获胜的可能性大小呢？

现在看来，这个问题对于熟知概率论的人来说相当简单：接下来每次抛硬币时都会出现两种等可能性的结果：正面向上或反面向上。在前5次已经出现2次反面、3次正面的基础上，第6次抛硬币时，若正面朝上，则梅雷爵士获胜；若反面朝上，则是平局，需要再抛硬币，第7次抛硬币时，正面向上则梅雷爵士获胜，反面向上则罗尼兹公爵获胜。总体来看，梅雷爵士的获胜概率为75%（50%+ 50%×50%=75%），罗尼兹公爵的获胜概率为25%（0+50%×50%=25%），所以，他们应该按照75：25这一比例分配赌金，即梅雷爵士分得75金路易，罗尼兹公爵分得25金路易。（二）帕斯卡发明概率论

帕斯卡持续研究一年后，1654年，帕斯卡与另一位数学家皮埃尔·德·费马（Pierre de Fermat，费马当时比帕斯卡大22岁，被誉为“业余数学家之王”，公众比较熟知的是费马大定理）通过信件探讨这个问题，其中一封信被公认为是概率论诞生的标志。在这封信件中，帕斯卡不仅对赌金分配问题提出了解决办法，还推出了一组公式，用来描述等概率事件如何组合产生复合概率，该研究成果可以用来解决与赌金分配问题类似的具有普遍性的不确定性问题。

根据新修订的第五代国家标准《中国地震动参数区划图》(GB18306-2015)[7]，云南全省国土面积84%位于地震烈度VII度以上，是全国平均水平的两倍。随着经济建设不断向山区、河谷等地震高风险区发展以及人口增加、城镇化进程的加速、经济发展GDP的快速增长等因素，暴露于地震灾害高风险区的生命财产总量增加，20世纪80年代以后，特别是21世纪以来，云南地震灾害损失急剧加大。2014年鲁甸地震与景谷地震造成了逾270亿元的直接经济损失，占全省GDP总量的近3%，其中，鲁甸MS6.5级地震直接经济损失近200亿元，是1996年丽江MS7.0级地震损失的近50倍。

在之后的50年中，由于帕斯卡的洞察力和影响，荷兰天文学家克里斯蒂安·惠更斯写了一本概率论初等教材。保险业也受到了积极的影响，保险业对承保风险的评估不再是完全依靠主观判断了，而是逐渐运用基于概率论的风险评估方法。

帕斯卡

二、期望值与理性选择

不确定条件下的选择确实令人头痛，比如最简单的选择——早上出门要不要带雨伞——就常常令人们举棋不定，因为无论带伞还是不带伞，都无法使我们在任何情况下都感觉自己的选择是最佳的，具体而言，无论是“带伞了没下雨”还是“不带伞下雨了”，人们都可能会觉得自己早上的决策有误。

帕斯卡想为上述问题寻找解决方案，于是，在解决赌资分配问题的同时，帕斯卡还试图弄明白，怎样将“对未来得失的估计”与“对未来事件可能性的估计”结合起来，进而确定哪种行动方案会产生最优结果。

（一）期望值的发明——将事件可能性和事件结果综合考虑

要确定在不确定条件下哪种行动方案会产生最优结果，首先需要对不确定条件下任一行动方案的价值进行评估，以便对不同行动方案的价值进行比较，进而选择最优行动方案。

在法国逻辑学家安托万·阿尔诺（Antoine Arnauld）与Pierre Nicole于1662年出版的《思维的艺术》一书中，阿尔诺（据推测是在帕斯卡的帮助之下，因为阿尔诺与帕斯卡是朋友，而且在《思维的艺术》出版之前，帕斯卡已经提出了著名的关于上帝是否存在的“帕斯卡赌注”）表达了这样的思想，“为了决定该做什么而获得收益或避免损失，我们既要考虑收益和损失本身，还要考虑它们发生或不发生的概率，而且，当把它们综合到一起时，我们还有必要从几何学的角度对他们所占的比例进行审查。”阿尔诺还讲道：“将后果和概率进行综合考虑，可以使我们更加理性地看待希望和恐惧。例如，许多人一听到雷声就惊恐万分。如果雷声会让他们想到上帝、死亡和幸福，那倒无可厚非。但如果仅仅是因为害怕被闪电击毙而惴惴不安的话，那就显然是不合情理的，因为每200万人中最多只有一人死于此种方式……所以面对某种伤害所表现出来的恐惧，不仅要与伤害的严重性相称，还要与伤害事件发生的可能性相称。”

经过进一步的研究，帕斯卡构造出了一个将可能性与后果两者结合起来的公式：把事件的概率同该事件的货币价值相乘，求出期望值。这样，人们就可以用期望值这个单一数值，对不确定条件下任一行动方案带来的价值进行评估。（二）不确定条件下的理性选择理论：期望值最大化

在发明期望值后，帕斯卡和阿尔诺认为，对于不确定条件下行动方案的选择问题，最优行动方案就是使期望值最大化的行动方案。以早上出门是否带伞的决策为例，人们不应该纠结于在任何情况（下雨或不下雨）下都要正确，而是应该计算带伞和不带伞两种行动方案下的期望价值（当然，这里各种组合情况下的价值需要决策者进行主观评估）。

由此，如何在不确定条件下做出最优决策，人类第一次有了一种确切的数学方法，即选择可产生最大期望值的行动方案，称之为“期望值理论”。例如，假设我们可以花20元参加抽奖，而且必须在如下两种抽奖中选择一种参加，一种是有50%的概率赢得30元，一种是有2%的概率赢得1000元。按照帕斯卡发明的期望值计算法，可以计算得到第一种抽奖的期望值为15元（50%×30= 15），第二种抽奖的期望值为20元（2%× 1000=20）。按照帕斯卡发明的最优选择理论，我们应该选择后一种抽奖方案。

某行动方案的期望值，其现代表述为：

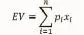
其中，pi和xi分别表示该行动方案的每一可能结果的出现概率和金钱价值，i=1，…，n。

科学届认为，不确定条件下的理性选择，就是选择可产生最大期望值EV的行动方案。这就是17世纪时人类发展出的不确定条件下的理性选择理论。

三、期望效用与理性选择

（一）圣彼得堡悖论

帕斯卡发明期望值理论约40年后，随着该理论被传播、理解和应用，尼古拉斯·伯努利（Nicholas Bernoulli）于1713年9月在写给数学家M·de Montmort的信中提出了一个彼得和保尔的赌博问题：“彼得掷一枚硬币，如果第一次掷硬币头面朝上，彼得答应给保尔1个荷兰盾［保尔在第一次抛硬币中的期望收益为1/2（=1/2×1）荷兰盾］；如果第一次掷的结果是背面朝上，则掷第二次，如果第二次掷硬币头面朝上，彼得付保尔2个荷兰盾［保尔在第二次抛硬币中的期望收益为1/2 （=1/2×1/2×2）荷兰盾］；如果第二次掷的结果是背面朝上，则掷第三次，如果第三次掷硬币头面朝上，彼得付保尔22个荷兰盾［保尔在第三次抛硬币中的期望收益为1/2 （=1/2×1/2×1/2×22）荷兰盾］；如果第三次掷的结果是背面朝上，则掷第四次……，到第n次，如结果是头面朝上，彼得付保尔2n-1个荷兰盾｛保尔在第n次抛硬币中的期望收益为1/2［=(1/2)n×2n-1］荷兰盾｝。这个赌局可以无限次地玩下去，直到头面朝上，保尔赢到钱为止。保尔在该赌局中所获的价值的期望值是多少？”

尼古拉斯·伯努利之所以提出这个问题，是由于他发现彼得参与这个赌局的期望收益与现实中该赌局的参与价之间相差实在太大。他发现，保尔参与这个赌局的期望收益为历次抛硬币的期望收益之和：1/2+1/2+1/2+……=∞。保尔参与这个赌局的期望收益为无穷大，按照帕斯卡的期望值理论，他应该拿出自己所有的钱，甚至大量举债来购买这个赌博机会，但是，现实中，这一赌局的卖价却从未超过20荷兰盾，这严重背离了当时的主流理论——帕斯卡发明的期望值理论，被称为“圣彼得堡悖论”。（二）对风险态度的考量

18世纪早期，圣彼得堡悖论成了概率论中的研究热点，好多欧洲数学家都想知道为何会出现这种现象。1738年，这一悖论被尼古拉斯·伯努利的表弟——瑞士物理学家、数学家丹尼尔·伯努利（Daniel Bernoulli，被称为“流体力学之父”，理工科出身的人熟悉其发现的“伯努利定律”和“伯努利方程”）解决。

丹尼尔·伯努利认为期望值的计算无误，但让人们按照期望值最大化法进行决策却不合理，因为期望值理论暗含一个假定：“人们对风险无动于衷”，而这一假定与现实严重不符。例如，有两个抽奖机会可供选择，抽奖A为“有100%的机会赢得10万元”，抽奖B为“有50%的机会赢得20万元”，参加A和B的期望收益相同，均为10万元。按照帕斯卡的期望值理论，决策者应该认为A和B无差异，选哪个都行。但实际上绝大多数人都会选择A。丹尼尔·伯努利把这种现象归因为：人类是谨慎的，通常不愿意冒险。

于是，丹尼尔·伯努利进一步考虑人们对风险的考量，试图总结出人们面对风险时的思考规律。大概的思路是这样的，假如甲一贫如洗，急需用钱满足家里最基本的温饱需求，此时他面临两个选择，一是有100%的机会赢得1万元，二是有50%的机会赢得2万元。可以预测，甲几乎肯定会选取100%赢得1万元，因为他急需用钱，不愿因为冒险而导致自己最爱的人挨饿受冻。两个选择的期望收益相等，甲选择无风险的第一种选择，显示甲是不愿意冒险的，表现出“风险厌恶”。为了度量甲的风险厌恶程度，可以通过增加第二个选择的支付金额，直到甲认为两个选择对他具有相同的吸引力为止，如50%的机会赢得2.5万元、3万元、3.5万元……如果甲认为“50%的机会赢得4万元”与“100%赢得1万元”具有相同的吸引力，那么，正如丹尼尔·伯努利提出的，在甲的心理上，确定地获得的4万元带给他的心理价值仅相当于得到1万元时的2倍。因为只有这样，甲才会认为这两个选择“50%的机会赢得4万元”和“100%赢得1万元”具有相同的吸引力。

让我们继续考虑甲的故事，假如甲由于工作努力并且抓住了好机会，现在达到中产水平，拥有资产100万元，其财富完全可以满足自己的基本需求，并不急于用钱，此时甲面临两个选择：一是有100%的机会赢得1万元，二是有50%的机会赢得2万元。结果，甲还是选择100%赢得1万元，表现出风险厌恶。我们仍然通过增加第二个选择的支付金额，直到甲认为两个选择的吸引力相同为止。结果，甲认为“50%赢得3万元”与“肯定赢得1万元”具有相同的吸引力，其风险厌恶程度相对一贫如洗时显著下降了。按照丹尼尔·伯努利的思维，这说明，在甲的心理上，此时3万元的价值大约相当于1万元的2倍。

丹尼尔·伯努利由此总结出三点极具价值的结论：第一，所得的心理价值与所得的数学价值（或金钱价值）是两个相互联系但不同的概念；第二，人们并不是像帕斯卡所认为的那样根据期望值进行决策，而是根据期望效用（丹尼尔·伯努利用效用来表示心理价值，以下类同）进行决策，期望效用应该是由“所得的概率”和“所得的效用（而不是金钱价值）”结合计算而来的；第三，比起那些一无所有的穷人，富人更愿意冒险。

◤图1　财富与心理价值的关系曲线（效用函数曲线）

（三）不确定条件下的理性选择理论：期望效用最大化

在发现“所得的效用（心理价值）”与“所得的数学价值（或金钱价值）”是两个相互联系但不同的概念后，丹尼尔·伯努利创造了一种可将数学价值和效用联系起来的简单形式，即用二维平面图来表示数学价值和效用之间的关系，并且认为这个图形应该描述或反映上述案例所表现的人类的两个特点：一是一贫如洗、财富很少时，4万元的心理价值约为1万元的2倍；二是富人比穷人更愿意冒险，财富达到100万元时，3万元的价值大约相当于1万元的2倍。丹尼尔·伯努利认为这个图形应该是一条凹曲线，如图1所示。可以看出，丹尼尔·伯努利的这条曲线与经典经济学中人类的效用曲线一致，呈现边际效用递减的特征。

将“所得的数学价值”转换为“效用”后，丹尼尔·伯努利修正了帕斯卡的期望值理论，现在称其为“期望效用理论”。在期望效用理论中，未来事件的概率与期望值理论中完全一致，不同的是用效用（心理价值）替代了数学价值（或金钱价值）。丹尼尔·伯努利认为，在不确定条件下人们会追求期望效用最大化而不是期望值最大化。

按照期望效用理论，某一行动方案的期望效用计算方法如下：

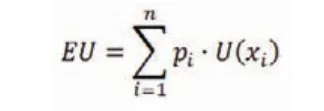
其中，pi、xi和U(xi)分别表示该行动方案的每一可能结果的出现概率、金钱价值和效用（心理价值），i=1，…，n。

按照丹尼尔·伯努利的理论，理性人会选择最优行动方案，最优方案就是期望效用EU最大的方案。这就是18世纪时人类发展出来并一直延续至今的不确定条件下的理性选择理论。

保险决策属于典型的不确定决策，因此，所谓对的或者理性的保险决策，就是指按照期望效用理论最大化原则作出的保险决策。理性保险决策理论的细节将在《什么是对的保险决策？——理性保险决策理论及其由来（下）》中介绍。