鸡群优化算法投影寻踪洪旱灾害评估模型

崔东文

(云南省文山州水务局,云南文山 663000)



鸡群优化算法投影寻踪洪旱灾害评估模型

崔东文

(云南省文山州水务局,云南文山 663000)

摘要:利用15个复杂函数对鸡群优化算法进行仿真验证,并同狼群算法、粒子群算法、鱼群算法和遗传算法进行对比。利用鸡群优化算法搜寻投影寻踪模型最佳投影方向,建立鸡群优化算法-投影寻踪洪旱灾害评估模型。以文山州1990—2013年洪旱灾害评估为例,分别选取受灾人口等5个洪灾评估指标及农作物受灾面积等4个旱灾评估指标,利用洪旱灾害投影系列均值及标准差构造洪旱灾害评估分级标准对实例进行评估。结果表明:鸡群优化算法具有较好的计算鲁棒性和全局寻优能力。将该算法用于投影寻踪模型最佳投影方向的选取,可有效提高评估精度,避免最佳投影方向寻优结果变化范围过大的缺陷。

关键词:洪旱灾害评估;投影寻踪;鸡群优化算法;算法验证;文山州

洪旱灾害在我国发生频率高、危害范围广,不仅造成严重经济损失,而且易引发滑坡、泥石流等次生地质灾害,加剧干旱缺水、水土流失以及水污染等生态环境灾害,严重影响、制约经济社会的发展。开展洪旱灾害评估对于客观评估灾区社会经济影响,为防汛抗旱、民政救灾等部门提供决策依据,以及提高洪旱灾害管理效率具有重要意义。目前用于洪灾评估的方法有GIS法[1]、模糊综合评判法[2]、层次分析法[3]、神经网络法[4]以及投影寻踪法[5]等,用于旱灾评估的方法有可变模糊集法[6]、突变评价法[7]、小波分析法[8]、Z指数法[9]以及投影寻踪法[10]等,这些方法均在洪旱灾害评估中取得了一定的实际应用。投影寻踪(projection pursuit,PP)是处理和分析高维数据的一类新兴统计方法,其基本思想是将高维数据投影到低维子空间上,并在该子空间上寻找出能够反映原高维数据结构或特征的投影,从而达到研究和分析高维数据的目的[11-12],在克服“维数祸根”以及解决小样本、超高维等问题中具有明显优势。在实际应用中,投影寻踪模型最佳投影方向a的选取对于投影寻踪模型的评估精度及评估结果有着关键性影响。目前,用于投影寻踪模型最佳投影方向选取的智能方法有遗传算法(genetic algorithm, GA)[5]及其改进算法[12-13]、粒子群优化(particle swarm optimization, PSO)算法[14]、人工鱼群算法(artificial fish swarm algorithm, AFSA)[15]、人工蜂群(artificial bee colony, ABC)算法[16]、混合蛙跳算法(shuffled frog leaping algorithm, SPLA)[17]、蚁群优化(ant colony optimization, ACO)算法[18],这些方法在提高投影寻踪模型预测或评估精度上取得了较好的效果。目前,群体智能仿生算法大有方兴未艾之势,除上述提到的人工鱼群等群体智能仿生算法[16-19]外,一些新型仿生算法被提出,并在函数优化、工程应用等领域得到应用,如狼群算法(wolf pack algorithm, WPA)[19]、布谷鸟搜索( cuckoo search, CS)[20]算法、果蝇优化(fruit fly optimization algorithmand, FOA)算法[21]群居蜘蛛优化(social spider optimization, SSO)[22]算法和鸡群优化(chicken swarm optimization,CSO)算法[23]等。Meng等[23]于2014年通过模拟具有等级秩序的鸡群觅食行为而提出了一种新型群体智能仿生算法——鸡群优化算法,这是一种全局优化算法,具有较好的收敛精度和鲁棒性能,已被证明在函数优化问题上性能要优于粒子群优化算法、差分进化(differential evolution,DE)算法和蝙蝠算法(bat algorithm,BA)[23]。

由于洪旱灾害受人类活动、自然环境以及气候变化等诸多因素的影响,时常表现为洪、旱灾害交替发生,甚至交织发生的局面,单独针对洪灾或旱灾进行评估,并不能客观、全面地反映某一年度区域灾害影响程度或变化趋势。本文首先利用15个复杂函数对鸡群优化算法进行仿真验证,并同狼群算法、粒子群算法、鱼群算法和遗传算法进行对比,以验证该算法的有效性;然后选取农作物受灾面积、受灾人口、死亡人口、倒塌房屋间数、直接经济损失作为洪灾评估指标,选取农作物受灾面积、成灾面积、粮食损失、经济作物损失作为旱灾评估指标,构建鸡群优化算法-投影寻踪洪旱灾害评估模型,采用洪旱灾害投影系列均值z-及标准差σ构造洪旱灾害评估分级标准,以文山州1990—2013年洪旱灾害评估为例进行实例验证。

1 鸡群优化算法-投影寻踪洪旱灾评估模型

1. 1 投影寻踪模型

投影寻踪模型的基本原理是将高维数据通过某种组合投影到低维子空间上,通过极小化投影指标来反映原高维数据结构或特征,并在低维空间上对数据结构进行分析,以达到研究和分析高维数据的目的,其简要算法过程[10 -11,24]如下:

步骤1:数据预处理。对评估数据集进行归一化处理。

步骤2:构造投影指标函数。投影寻踪方法就是将m维数据{xijj=1,2,…,m}综合成以a=(a1, a2,…,am)为投影方向的一维投影值zi:

式中xij为第i年第j个评估指标值;a为单位向量。

步骤3:优化投影指标函数。当投影指标函数取得最大值时,所对应的a方向为最能反映数据特征的最优投影方向。因此搜寻最优投影方向问题就转化为非线性最优求解问题,其目标函数Q(a)及约束条件为

式中:σ、Dz分别为投影值zi的标准差和局部密度;-z为序列zi的平均值;R为局部密度的窗口半径;rij为样本之间的距离;o(τ)为单位阶跃函数,当τ≥0时,其值为1,τ＜0时,其值为0;n为评估样本总年数。

步骤4:分级标准。由于洪旱灾害投影系列均值-z反映的是集中趋向,而标准差σ反映的是相对离散程度,因此,可利用-z及σ构造洪旱灾害评估分级标准,并将洪旱灾害分为4个等级:特大[-z+σ,∞)、重大[-z,-z+σ)、较大[-z-σ,-z)和一般(0,-z-σ)。其中-z计算公式为

步骤5:评估。将最佳投影方向a代入式(1)得到各年度投影值zi,依据洪旱灾害分级标准进行评估。

1. 2 鸡群优化算法

鸡群优化算法[23]是模拟鸡群觅食行为的一种随机优化算法,其算法遵行以下4个理想化规则:

规则1:存在多组鸡群,每一组包括若干占主导地位的公鸡,母鸡和雏鸡。

规则2:依据适应度值判定鸡群个体身份(公鸡、母鸡和雏鸡),将适应度值最优的几个个体判定为公鸡,他们将作为每一组的头领;适应度值最差的判定为雏鸡,其他个体判定为母鸡。母鸡随机选择一组生活,且“具有母子关系”的母鸡和雏鸡之间的关系也是随机的建立。通过建立等级秩序,不同鸡群间可以协同觅食,以及种群更新,包括个体死亡、雏鸡成长变成公鸡或母鸡,母鸡孵育后代。

规则3:在任一组中公鸡、母鸡、雏鸡的等级秩序将维持不变,仅随迭代过程进行更新。

规则4:鸡群跟随公鸡觅食,雏鸡在母鸡周围觅食,公鸡在食物竞争上具有最大优势,母鸡次之,雏鸡最不具优势。

针对优化问题为极小值,最小适应度值所对应鸡的所处空间位置即为待优化问题的最优解。以下从数学角度对鸡群优化算法机理进行描述[24]。

设搜索食物空间为D维,种群规模为N,第i只公鸡在j维空间t时刻的位置为xtij(i=1,2,…,N;j= 1,2,…,D),则在t+1时刻的位置按下式更新:

式中:ε为不等于0的较小常数;k为从公鸡组中随机选择的第k只公鸡,k≠i;fi、fk(k = 1,2,…,N)分别为第i、k只公鸡所对应的适应度值;randn(·)为正态分布随机数。

第i只母鸡在j维空间t+1时刻的位置可用数学表达式描述如下:

式中:rand为[0,1]上均匀分布的随机数;r为从母鸡配偶中随机选择的第r只公鸡;s为从鸡群中随机选择的第s只公鸡或母鸡,r≠s。

t+1时刻在母鸡周围觅食的第i只雏鸡在j维空间的位置为

式中F∈[0,2]为随母鸡觅食的雏鸡随机参数。

从上述算法及文献[23]来看,鸡群优化算法具有如下优点:①可以有效地提取优化问题,具有自适应优化能力。②鸡群多种位置更新策略有利于在确定性与随机性之间取得平衡,扩大了搜索空间。③将鸡群分为G组,即多种群策略有利于快速收敛到全局最优解,但过大的G不利于算法收敛到全局最优,而过小的G易使算法陷入局部最优。经过初步测试,G∈[2,20]能满足大多数优化问题。④通过建立等级秩序,不同鸡群间可以协同觅食。鸡群个体的死亡、雏鸡成长变成公鸡或母鸡、母鸡孵育后代等进化策略有利于鸡群保持种群多样性,使算法不易陷入局部极值。

1. 3 鸡群优化算法-投影寻踪洪旱灾害评估步骤

鸡群优化算法-投影寻踪洪旱灾害评估模型计算步骤[23]可归纳如下:

步骤1:数据预处理。利用式(1)对数据进行归一化处理,设置鸡群数量N、公鸡数量R、母鸡数量H、小鸡数量C和具有“母子关系”的母鸡数量M,鸡群分组数目G,随机参数F和最大迭代次数T。

步骤2:等级秩序的建立。依据鸡群体行为的4个理想化规则建立等级秩序;将鸡群分为G组,随机建立母鸡和小鸡之间的对应关系。

步骤3:确定目标函数。由于鸡群优化算法是求解极小值,因此将式(2)的倒数作为目标函数,即以下式作为适应度函数:

步骤4:初始化操作。随机初始化鸡的位置xtij,由式(8)计算目标函数适应度值,选取当前最佳适应度值及所对应个体所处空间位置。

步骤5:迭代。对随机选择的第i只鸡为公鸡、母鸡、雏鸡时,分别按式(4)(6)(7)进行位置更新。

步骤6:适应度函数计算。依据更新位置,由式(8)计算适应度值,若更新后的适应度值优于当前最佳适应度值,则替换当前最佳个体所处空间位置,并将更新后的适应度作为当前最佳适应度值;若劣于当前最佳适应度值,则不进行个体空间位置替换。

步骤7:找出当前最佳个体适应度值及所处空间位置。判断算法迭代终止条件是否满足,若满足则转至步骤8,否则重复执行步骤4～7。

步骤8:输出最优个体值和全局极值,即a和Q′(a),算法结束。

步骤9:构造分级标准。利用洪旱灾害投影系列均值z-及标准差σ构造洪旱灾害评估分级标准。

步骤10:评估。将a代入式(1)得到各年度洪旱灾害投影值zi,并依据所构造分级标准进行洪旱灾害评估。

2 算法验证

为全面客观评价鸡群优化算法性能,本文选取文献[19]中15个复杂函数作为验证对象,并将鸡群优化算法寻优结果与文献[19]中狼群算法(WPA)、粒子群算法(PSO)、人工鱼群算法(AFSA)及遗传算法(GA)的寻优结果进行比较,基准函数参见文献[19]。为了便于与文献[19]WPA等的寻优结果进行客观公正的比较,鸡群优化算法参数设置为: T=2000,N=50、R=0. 3N、H=0. 6N、M=0. 1N, G=500, F∈[0. 5,0. 9]。采用Matlab2010a的M语言编程,用鸡群优化算法对15个复杂函数重复进行100次寻优计算,当满足式(9)时,即认为当前寻优计算成功。

式中:V为函数的理想最优值;V*为每次寻优计算所得最优函数值。

表1为鸡群优化算法及文献[19]中4种算法对15个复杂函数的寻优计算结果统计,若寻优结果小于1×10-16,则视为0。

表1 函数优化对比结果

续表

从表1可知:①与粒子群算法、人工鱼群算法和遗传算法相比,鸡群优化算法的寻优结果除Easom、Trid6两个单峰不可分函数劣于粒子群算法和遗传算法外,其余函数寻优结果均优于粒子群算法、人工鱼群算法和遗传算法,尤其是在Matyas、Sumsquares、Sphere、Bohachevsky1、Eggcrate、Schaffer、Six Hump Camel Back、Bohachevsky3、Bridge和Rastrigin函数上鸡群优化算法具有较好的寻优效果,表现出较高的寻优精度和较好的算法执行能力;②与狼群算法相比,鸡群优化算法的寻优结果除Trid6、Quadric和Ackley函数外,其余函数寻优结果均不劣于或优于狼群算法,如Easom、Booth、Bridge函数;③对于低于60维的函数,鸡群优化算法表现出较好的寻优效果,优于狼群算法;对于特高维函数,如120维的Quadric函数、200维的Ackley函数,鸡群优化算法的寻优效果略逊于狼群算法,但远优于粒子群算法、人工鱼群算法和遗传算法。这表明鸡群优化算法具有较好的计算鲁棒性和全局寻优能力。

鸡群优化算法中参数设置并不多,主要有R、H 和G。经验证,R设置为0. 2N～0. 3N、H为0. 6N～0. 8N时对计算性能的影响并不显著。对于相对复杂的函数,G对计算有显著影响,一般随G的增大,寻优精度会显著提高;较大的G有利于收敛到全局最优,而过小的G易陷入局部最优;一般而言,G处于100～1000之间时具有较理想的寻优效果。

3 应用实例

3. 1 数据来源

文山州位于云南省东南部,地处低纬度高原季风气候区域,辖文山、砚山、西畴、麻栗坡、马关、丘北、广南、富宁8县(市),东邻广西,北接曲靖,西与红河州毗邻,南与越南接壤,全州总面积31456km2,分属珠江、红河两大流域。据《文山壮族苗族自治州水利电力志》,1672—1949年的278年间,共记载洪灾41次,其中文山城27次。1950—2013年的64年间,有较大洪灾35次,而局部洪灾则连年发生。2009年以来,文山州遭受了历史罕见的持续干旱,对工农业生产造成了巨大损失,其干旱范围之广、历时之长、程度之深、损失之重历史罕见。据统计,此次旱灾导致全州8县(市)102个乡镇283万人直接受灾,历时近4 a,持续时间与有记载的1924—1926年连旱时间相当,造成全州农林畜业直接经济损失36. 83亿元。因此,开展洪旱灾害评估对于科学评估灾区社会经济影响,保障人民群众生命财产安全和全面建设小康社会具有重要意义。本文选取农作物受灾面积、受灾人口、死亡人口、倒塌房屋间数、直接经济损失作为洪灾评估指标;选取农作物受灾面积、成灾面积、粮食损失、经济作物损失作为旱灾评估指标。文山州1990—2013年洪旱灾害评估指标如表2所示。

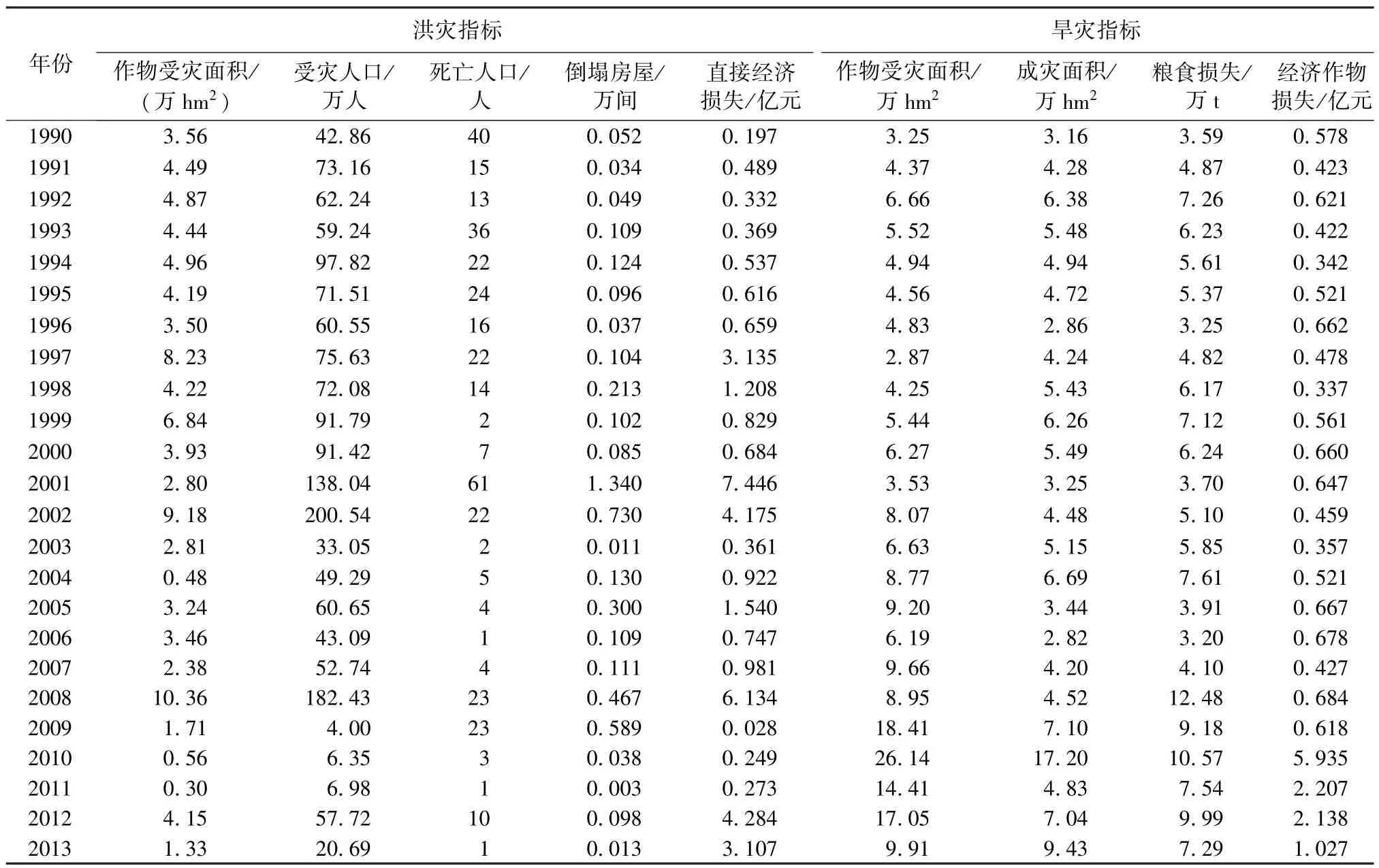
表2 文山州1990—2013年洪旱灾害评估指标

3. 2 鸡群优化算法计算结果

参数设置同上,搜索区间为[0,1],连续计算4 次,得到一致的结果,其进化过程如图1所示。

图1 鸡群优化算法进化过程

4次计算的Q′(a)均为0. 001 016 75(洪灾)、0. 00124877(旱灾),a均为(0. 4447,0. 4492,0. 4812, 0. 5403)(洪灾)和(0. 5487,0. 4881,0. 4673,0. 4923) (旱灾),收敛稳定;从图1可知, 4次计算均在迭代次数为30左右时收敛到全局最优解,具有较快的收敛速度。

3. 3 分级标准与评估结果

利用上述a值,可计算得到洪灾和旱灾投影系列均值z-分别为0. 55、0. 43,标准差σ分别为0. 44、0. 40,据此,构造4个等级的洪旱灾害分级标准:特大洪灾[0. 99,∞)、重大洪灾[0. 55,0. 99)、较大洪灾[0. 11,0. 55)、一般洪灾(0,0. 11)和特大旱灾[0. 83,∞)、重大旱灾[0. 43,0. 83)、较大旱灾[0. 03, 0. 43)、一般旱灾(0,0. 03)。

将a值代入式(1)得到文山州1990—2013年洪旱灾害投影值zi,并依据所构造的分级标准进行洪旱灾害评估,结果见表3和图2。

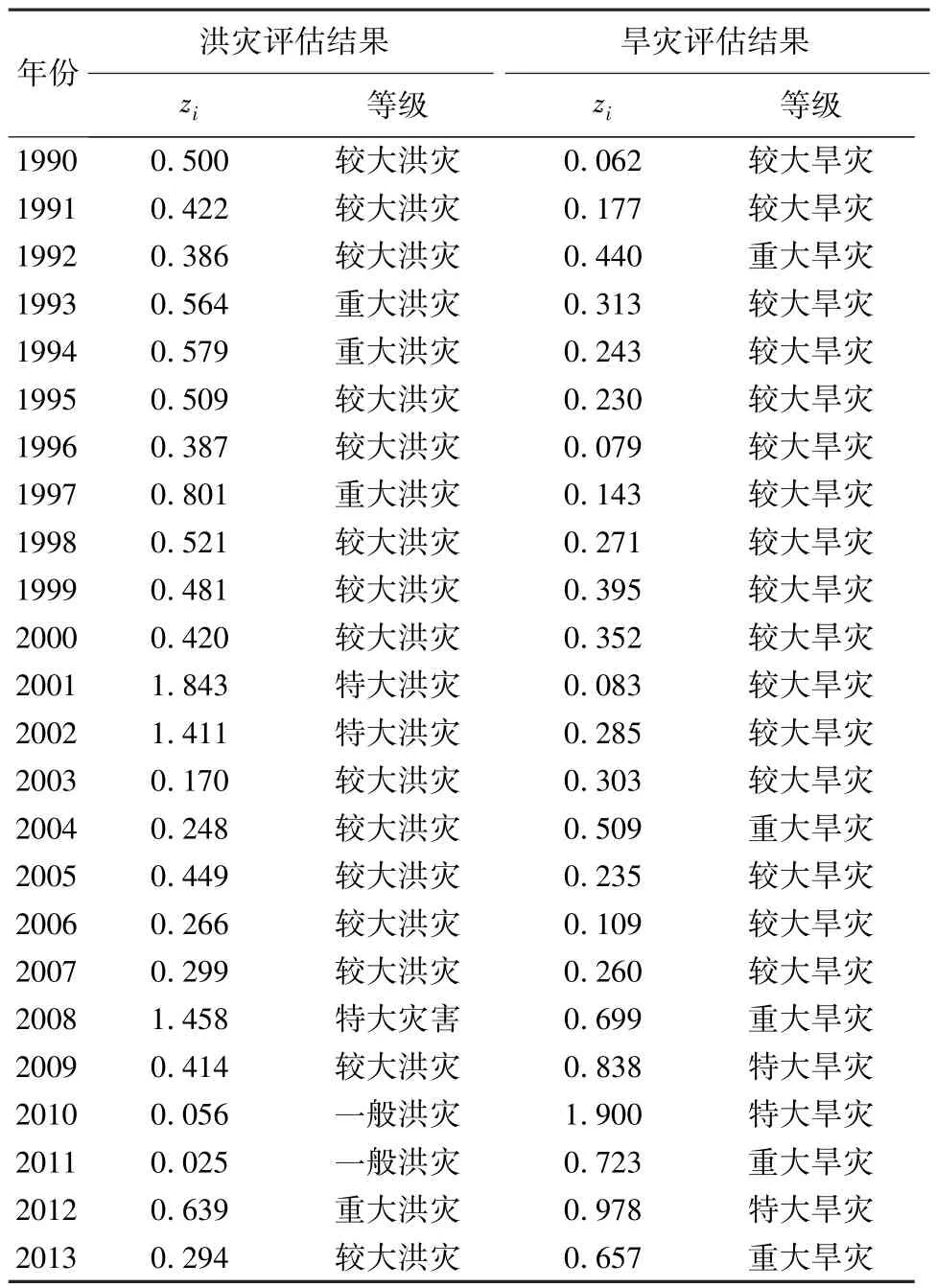
表3 文山州1990—2013年洪旱灾害评估结果

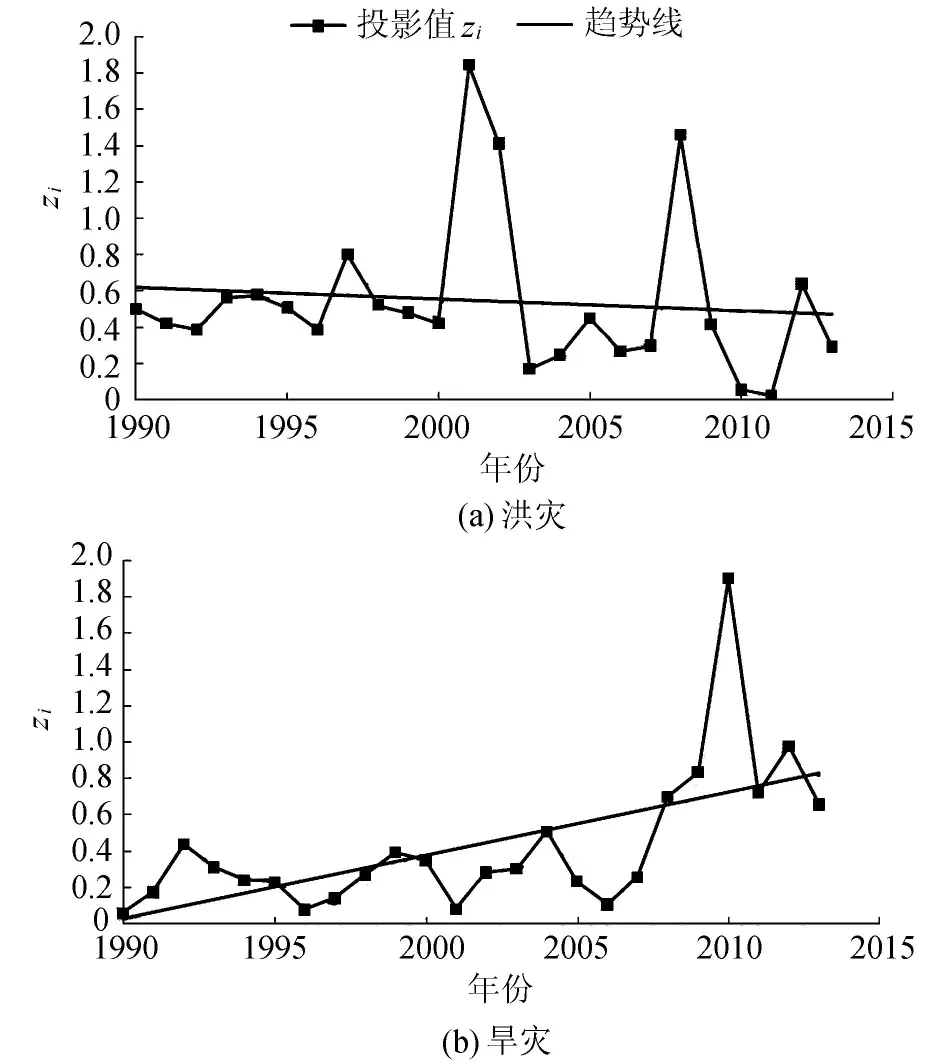
图2 投影值变化趋势

文山州1990—2013年洪灾评估结果为:特大洪灾3次,重大洪灾4次,较大洪灾15次,一般洪灾2次。经计算,投影值zi的Spearman统计量与Kendall统计量分别为1. 56和1. 48,均小于置信水平为0. 05时的相应临界值2. 01和1. 96,表明文山州洪灾呈减弱趋势,但不显著。a的各分量aj均为正值,说明各评价指标投影方向一致,其中a5(直接经济损失投影分量)最大,说明洪灾对直接经济损失影响最大,其次为倒塌房屋间数、死亡人口和受灾人口,而对农作物受灾面积影响最小。

文山州1990—2013年旱灾评估结果为:特大旱灾3次,重大旱灾5次,较大旱灾16次。经计算,投影值zi的与分别为2. 19和3. 08,均大于置信水平为0. 05时的相应临界值2. 01和1. 96,表明文山州旱灾呈增强趋势,且趋势显著。a的各分量aj均为正值,说明各评价指标投影方向一致,其中a1(农作物受灾面积投影分量)最大,说明旱灾对农作物受灾面积影响最大,其次为经济作物损失和成灾面积,而对粮食损失影响相对较小。

4 结 论

a.提出鸡群优化-投影寻踪洪旱灾害评估模型,利用鸡群优化算法寻找投影寻踪模型最佳投影方向a,可有效避免a的寻优结果变幅过大,提高投影寻踪模型的评估可靠度,为确定投影寻踪模型的最佳投影方向提供了一种全新的方法。

b.通过15个复杂函数对鸡群优化算法进行仿真验证,并与狼群算法、粒子群算法、人工鱼群算法和遗传算法进行对比,结果表明鸡群优化算法具有较好的收敛精度和全局寻优能力,是一种有效的新型全局优化算法。

c.利用洪旱灾害投影系列均值z-及标准差σ构造评估分级标准,可有效解决不同层面洪旱灾害评估中等级划分问题,具有较好的通用性。

d.从1990—2013年的洪旱灾害评估结果来看,文山州洪灾呈减弱趋势,但减弱趋势不显著,直接经济损失对文山州洪灾等级影响最大,农作物受灾面积影响最小;旱灾呈显著增加趋势,农作物受灾面积对文山州旱灾等级影响最大,粮食损失影响相对较小。

参考文献:

[ 1 ]莫建飞,陆甲,李艳兰,等.基于GIS的广西洪涝灾害孕灾环境敏感性评估[J].灾害学,2010,25(4):33-37. (MO Jianfei, LU Jia, LI Yanlan, et al. GIS-based sensitivity assessment on environment of developing flood hazards in Guangxi Province [ J ]. Journal of Catastrophology,2010,25(4):33-37. (in Chinese))

[ 2 ]刘合香,徐庆娟.区域洪涝灾害风险的模糊综合评价与预测[J].灾害学,2007,22(4):38-42. (LIU Hexiang, XU Qingjuan. Fuzzy comprehensive evaluation and prediction of regional flood disaster risk[J]. Journal of Catastrophology,2007,22(4):38-42. (in Chinese))

[ 3 ]崔东文.基于人工神经网络与主成分分析法的洪灾评估:以文山州1990—2007年洪灾评估为例[J].水资源研究,2011,32(2):37-39. (CUI Dongwen. Evaluation of flood disaster and artificial neural network based on principal component analysis: a case study in Wenshan 1990-2007 flood disaster evaluation[J]. Journal of Water Resources Research,2011,32(2):37-39 . (in Chinese))

[ 4 ]杨聪辉,王宝华,付强,等.洪水灾情评价的脉冲耦合神经网络模型[J].灾害学,2010,25(3):12-15. (YANG Conghui,WANG Baohua,FU Jiang,et al. Pulse coupled neural network model for evaluation of flood disaster [J]. Journal of Catastrophology, 2010, 25 (3): 12-15. ( in Chinese))

[ 5 ]陈曜,丁晶,赵永红.基于投影寻踪原理的四川省洪灾评估[J].水利学报,2010,41 (2):220-225. (CHEN Yao,DING Jing,ZHAO Yonghong. Assessment on flood disaster in Sichuan Province based on the principle of projection[J]. Journal of Hydraulic Engineering, 2010,41 (2):220-225. (in Chinese))

[ 6 ]周惠成,张丹.可变模糊集理论在旱涝灾害评价中的应用[J].农业工程学报,2009,25 (9):56-61. (ZHOU Huicheng, ZHANG Dan. Assessment model of drought and flood disasters based on variable fuzzy set theory [ J]. Transactions of the Chinese Society of Agricultural Engineering,2009,25(9):56-61. (in Chinese))

[ 7 ]唐明,邵东国,姚成林,等.改进的突变评价法在旱灾风险评价中的应用[J].水利学报,2009,40(7):858-862. (TANG Ming, SHAO Dongguo, YAO Chenglin, et al. Improved catastrophe theory based evaluation method and its application to drought disaster risk evaluation [ J]. Journal of Hydraulic Engineering,2009,40(7):858-862. (in Chinese))

[ 8 ]宋新山,王宇晖,严登华,等.基于分形特征的我国干旱灾害小波分析[J].系统工程理论与实践,2013,33 (11):2986-2992. (SONG Xinshan, WANG Yuhui, YAN Denghua,et al. Fractal and wavelet analysis on the 59 years time series of drought disaster ratio in China [J]. Systems Engineering:Theory & Practice, 2013, 33(11): 2986-2992. (in Chinese))

[ 9 ]杨晓华,杨小利.基于Z指数的陇东黄土高原干旱特征分析[J].干旱地区农业研究,2010,28(3):248-253. (YANG Xiaohua,YANG Xiaoli. Analysis of drought in the Loess Plateau of Longdong characteristics based on Z index [ J]. Agricultural Research in the Arid Areas, 2010,28(3):248-253. (in Chinese))

[10]余航,王龙,文俊,等.基于投影寻踪原理的云南旱灾评估[J].中国农学通报,2012,28 (8):267-270. ( YU Hang,WANG Long, WEN Jun, et al. Yunnan drought evaluation based on projection pursuit [ J ]. Chinese Agricultural Science Bulletin,2012,28(8):267-270. (in Chinese))

[11]付强,赵小勇.投影寻踪模型原理及其应用[M].北京:科学出版社,2006.

[12]王柏,张忠学,李芳花,等.基于改进双链量子遗传算法的投影寻踪调亏灌溉综合评价[J].农业工程学报, 2012,28(2):84-89. (WANG Bai,ZHANG Zhongxue,LI Fanghua, et al. Comprehensive evaluation of regulated deficit irrigation using projection pursuit model based on improved double chains quantum genetic algorithm [J]. Transactions of the Chinese Society of Agricultural Engineering, 2012,28(2):84-89. (in Chinese))

[13]付强,付红,王立坤.基于加速遗传算法的投影寻踪模型在水质评价中的应用研究[J].地理科学,2003,23 (2):236-239. ( FU Qiang, FU Hong, WANG Likun. Study on the ppe model based on raga to evaluating the water quality [J]. Scientia Geographica Sinica, 2003,23 (2):236-239. (in Chinese))

[14]陈广洲,汪家权,解华明.粒子群算法在投影寻踪模型优化求解中的应用[J].计算机仿真,2008,25(8):159-161. (CHEN Guangzhou,WANG Jiaquan,XIE Huaming. Particle swarm algorithm in the application in solving optimization projection pursuit model [ J ]. Computer Simulation, 2008,25(8):159-161. (in Chinese))

[15]丁红,刘东,李陶.基于改进人工鱼群算法的三江平原投影寻踪旱情评价模型[J].农业工程学报,2010,26 (12):84-88. (DING Hong, LIU Dong, LI Tao. Projection pursuit model for evaluating drought based on improved artificial fish swarm algorithm of Sanjiang Plain [ J]. Transactions of the Chinese Society of Agricultural Engineering, 2010,26(12):84-88. (in Chinese))

[16]赵建强,戴青松,陈必科,等.基于人工蜂群-投影寻踪法的南方某河水质综合评价研究[J].节水灌溉,2014 (8): 49-52. ( ZHAO Jianqiang, DAI Qingsong, CHEN Bike,et al. Study on the artificial bee colony-projection pursuit method based on a comprehensive assessment of water quality in South China[J]. Water Saving Irrigation, 2014(8):49-52. (in Chinese))

[17]王明昊,董增川,马红亮.基于混合蛙跳与投影寻踪模型的水资源系统脆弱性评价[J].水电能源科学,2014 (9):31-35. ( WANG Minghao, DONG Zengchuan, MA Hongliang. Assessment of water resources system vulnerability based on shuffled frog leaping algorithm and projection pursuit model [ J ]. Water Resources and Power, 2014(9):31-35. (in Chinese))

[18]候景伟,孔云峰,孙九林.蚁群算法在需水预测模型参数优化中的应用[J].计算机应用,2012,32(10):2952-2955. ( HOU Jingwei, KONG Yunfeng, SUN Jiulin. Application of ant colony algorithm for parameter optimization of water demand prediction model [ J]. Journal of Computer Applications, 2012, 32(10): 2952-2955. (in Chinese))

[19]吴虎胜,张凤鸣,吴庐山.一种新的群体智能算法:狼群算法[J].系统工程与电子技术,2013,35(11):2430-2438. (WU Husheng,ZHANG Fengming,WU Lushan. A new swarm intelligence algorithm: wolf pack algorithm [J]. Systems Engineering and Electronics, 2013, 35 (11): 2430-2438. (in Chinese))

[20] YNAG Xinshe, DEB S. Cuckoo search via Lévy flights [ C ] / / Proceedings of World Congress on Nature & Biologically Inspired Computing. Piscataway:IEEE,2009: 210-214.

[21]潘文超.果蝇最佳化演算法[M].台北:沧海书局, 2011.

[22] CUEVAS E, CIENFUEGOS M, ZALDíVAR D, et al. A swarm optimization algorithm inspired in the behavior of the social-spider[J]. Expert Systems with Applications, 2013,40(16): 6374-6384

[23] MENG Xianbing, LIU Yu, GAO Xiaozhi,et al. Advances in Swarm Intelligence [ J]. Lecture Notes in Computer Science,2014,8794:86-94.

[24]崔东文,郭荣. SSO-PP模型在水源地安全保障达标评价中的应用[J].水利经济,2015,33 (5):8-13 (CUI Dongwen,GUO Rong. Application of SSO-PP model in security standard evaluation of water sources. [J]. Water Conservancy Economy,2015,33(5):8-13. (in Chinese))

Projection pursuit model for evaluation of flood and drought disasters based on chicken swarm optimization algorithm

/ / CUI Dongwen(Wenshan Water Conserυancy Bureau of Yunnan Proυince, Wenshan 663000, China)

Abstract:The chicken swarm optimization algorithm was validated using 15 complex functions, and the simulated results were compared with those of the Wolf algorithm, particle swarm optimization algorithm, fish swarm algorithm, and genetic algorithm. Using the chicken swarm optimization to search for the optimal projection direction of the projection pursuit model, a projection pursuit evaluation model was established. Using assessment of flood and drought disasters from 1990 to 2013 in Wenshan Prefecture as an example, five flood disaster evaluation indices, including disaster-affected population, and four drought disaster evaluation indices, including the disaster area of crops, were selected, and grading standards for flood and drought disaster assessment were constructed with the mean and standard deviation of the flood and drought disaster projection series. The results show that the chicken swarm optimization algorithm is robust and has high global optimization ability. Using the algorithm to select the optimal projection direction of the projection pursuit model can effectively improve the evaluation accuracy and prevent a high degree of variation from occurring in the optimal projection direction.

Key words:flood and drought disaster assessment; projection pursuit; chicken swarm optimization algorithm; algorithm verification; Wenshan Prefecture

(收稿日期:2014- 12 31 编辑:郑孝宇)

作者简介:崔东文(1978—),男,高级工程师,主要从事水资源和水环境研究。E-mail:cdwgr@163. com

DOI:10. 3880/ j. issn. 1006- 7647. 2016. 02. 004

中图分类号:P426. 616

文献标志码:A

文章编号:1006- 7647(2016)02- 0016- 08