基于无网格方法的四叶草型催化剂体相温度分布数值模拟

王 阔，赵 波，秦 波，杜艳泽

(1.中国石化抚顺石油化工研究院，辽宁 抚顺 113001；2.辽宁石油化工大学理学院)

基于无网格方法的四叶草型催化剂体相温度分布数值模拟

王 阔1，赵 波2，秦 波1，杜艳泽1

(1.中国石化抚顺石油化工研究院，辽宁 抚顺 113001；2.辽宁石油化工大学理学院)

以四叶草型及圆柱型加氢裂化催化剂三维体相环境为计算实体，以模拟工业运行温度的函数作为边界条件，采用无网格数值方法求解傅里叶传热方程，并根据计算结果分析加氢裂化反应过程中工况条件及催化剂尺寸对于催化剂内部温度分布的影响。结果表明：在加氢裂化反应中，圆柱型及四叶草型催化剂颗粒内部的最高温度及平均温度均随反应放热量、空速、原料密度、催化剂半径及催化剂长度的增加而增大，其中反应放热量和催化剂半径对催化剂内部温度的影响更显著；即使在理想的宏观等温反应条件下，两种催化剂内部仍然是非等温区域；在工况条件及催化剂半径和长度均相同时，四叶草型催化剂内部的最高温度、平均温度均低于圆柱型催化剂，具有比圆柱型催化剂更均匀的温度分布。

加氢裂化催化剂 传热 无网格法 数值模拟 温度分布

油品的加氢裂化反应整体上为强放热反应，温度和热量是该类反应最重要的影响因素。有关加氢裂化反应体系的能量恒算以及节能研究的文献众多[1-2]，但一般仅限于较大空间尺度或单纯反应热层面[1-5]。对于小型实验装置，整个反应系统基本可以近似视为等温反应系统；而工业装置的反应系统则可以视为一个近似的绝热系统。在反应过程中，反应器内部的温度分布会影响催化剂床层不同位置的反应速率，进而影响该位置的热量释放，热量的传递又会引起体系温度分布的重新调整。这一温度的正反馈过程在加氢裂化工业生产中十分重要。

加氢裂化反应过程的热量集中于催化剂颗粒，每个催化剂颗粒都相当于反应体系的一个“微热源”。这些微热源的温度分布情况直接或间接影响反应体系的质量传递、热量传递、反应进程以及产品分布。同时，催化剂体相内部的温度分布对催化剂寿命也有极大的影响。因此，对催化剂体相内部的温度分布进行研究十分重要。传统的炼化工业一般采用热电偶测定温度，但只能得到反应器内部宏观点的温度近似值，无法对反应过程的实时微观热效应进行分析。近年来，虽然 “非接触式”的红外测温技术得到广泛发展[6]，但由于催化剂内部微小而复杂的形态结构，目前没有任何温度测量设备能够对其内部温度进行测量；同时，由于催化剂外观几何形态以及反应条件的复杂性，导致常规导热模型体系的经验公式难于适用。本课题基于傅里叶传热定律的数值模拟方法来解决这一类问题，以四叶草型和圆柱型加氢裂化催化剂三维体相环境为计算实体，以模拟工业运行温度的函数作为边界条件，采用无网格数值方法求解傅里叶传热方程，并根据计算结果分析加氢裂化反应过程中工况条件及催化剂尺寸对催化剂内部温度分布的影响。

1 模型建立与求解过程

1.1 傅里叶传热方程

对一般传热过程，当存在稳定热源时，体系温度对于空间的分布形态可由一个稳态傅里叶传热方程确立。对于一个三维体系，一般的数学形式如式(1)所示。

(1)

式中：F(x，y，z)表示体系内温度对于空间的函数，当空间点处于体相内部(v)时，整个体系由一个偏微分方程描述，其中qv(x，y，z)是体系的热源函数，该函数表示当体系存在热源或热汇时该热源或热汇对空间的分布形式；λ表示计算体系的导热系数，由该体系组成材料的物化性质决定。当温度点处于体相表面(σ)时，温度可以用第一型迪里克莱边界条件描述，可将表面温度分布表达为函数G(x，y，z)。对极少数具有比较简单的热源或热汇函数形式及比较规则的几何外观形态和边界条件的导热体系而言，函数F(x，y，z)存在解析形式。由于拉普拉斯型方程的初值问题的解是不稳定的[7]，对于绝大多数复杂实际工程的传热体系，对模型方程体系的适定性问题讨论极为复杂，式(1)只能由数值方法求解。

1.2 加氢反应过程热量衡算及相关方程参数的确立

整个加氢裂化过程的精确反应热计算比较困难，根据已有经验及文献，加氢裂化反应的放热量一般为200～500 kJkg，原料密度一般为0.85～1.05 kgL，反应过程的体积空速一般为0.9～1.5 h-1。通过以上数据可对反应体系进行热量衡算及方程参数估计。

取极端原料性质及操作条件进行方程参数估计。假定加氢裂化反应放热量Qm=500 kJkg，油品密度ρ=1.05 kg/L，则每加工1 L油品的放热量q=Qm×ρ=500 kJ/kg×1.05 kg/L=525 kJ/L。假定体积空速LHSV=1.5 h-1，则每升催化剂每小时的放热量Qv=q×LHSV=525×1.5=787.5 kJ/(L·h)，也即单位体积热功率P=787.5 kJ/(L·h)=218.75 W/L=2.187 5×10-4W/mm3。根据文献[8]，一般催化剂的导热系数为0.25～0.32 W/(m·K)，因此计算中导热系数λ取2.58×10-4W/(mm·K)，式(1)中相关热功率与导热系数的比值qv(x，y，z)/λ=(2.187 5×10-4W/mm3)/[2.58×10-4W/(mm·K)]=0.85 K/mm2。

1.3 无网格方法及计算过程

目前主要采用数值方法对较为复杂的工程偏微分方程进行求解，常规的数值方法包括有限差分方法(FDM)、有限元方法(FEM)。前者对于复杂边界条件的适应性很差，在现代工程计算应用中受到了一定的限制；后者自20世纪50年代开始兴起，堪称数值方法领域的一个里程碑，然而它也存在缺点和局限性，例如该方法需要在计算前对计算体系进行相关的网格划分，而形成网格的计算成本较高，特别是对于复杂的三维体系，生成复杂的高质量网格相当困难[9]。产生这类问题的根源在于有限元计算过程中使用了生成网格单元的相关连接信息。因此，近年来无网格类计算方法应运而生。无网格方法的特点以及与其它计算方法结合使用的案例参见文献[10-13]。

本课题使用无网格计算方法对三维傅里叶传热方程进行数值求解，并对具有不同几何形态的圆柱型及四叶草型催化剂的体相温度空间分布形式进行描述和分析，主要计算过程为：对指定采样点确定相关的三维长方体计算支持域，在支持域中选择具有局域性质的局域函数，该局域函数以多项式函数为基本函数；首先计算支持域内的计算节点局域矩阵，并选择三维长方体计算支持域中的三次样条权重函数；然后在支持域内构造权重矩阵，依据已定义的局域矩阵以及权重矩阵产生对于无网格计算采样点的形函数矩阵；将采样点形函数以及形函数的导数依次代入式(1)，构造出以计算点温度数值为未知向量的线性方程组，该线性方程组的系数矩阵及常数项矢量分别称为力矩阵和载荷矩阵，在载荷矩阵中可根据具体控制方程及边界条件加载相应的数据，根据计算需要，力矩阵的行数与列数(即采样点个数与计算点个数)可相同也可不同；最后用线性最小二乘法求解力矩阵对于载荷矩阵的未知向量，即得到计算节点温度函数的近似数值，再用计算节点温度函数的数值与生成的形函数矩阵重构整个采样节点温度函数的数值，便可获得原偏微分方程体系的近似数值解。

1.4 计算参数及边界条件的设定

相比于传统圆柱型催化剂，四叶草型催化剂具有较大的宏观外表面积以及在反应过程中具有较小的系统压降，因此得到了广泛应用。四叶草型催化剂的截面外观如图1所示。由图1可知，四叶草型催化剂包含两类半径，即4个相切的小圆柱体的半径r、与4个小圆柱体相切的外接大圆的半径R。相比于传统的半径为R的圆柱型催化剂，四叶草型催化剂具有更小的体积和更大的外表面积。本课题对具有不同大圆半径R及长度的圆柱型催化剂和四叶草型催化剂内部温度场进行计算和分析。

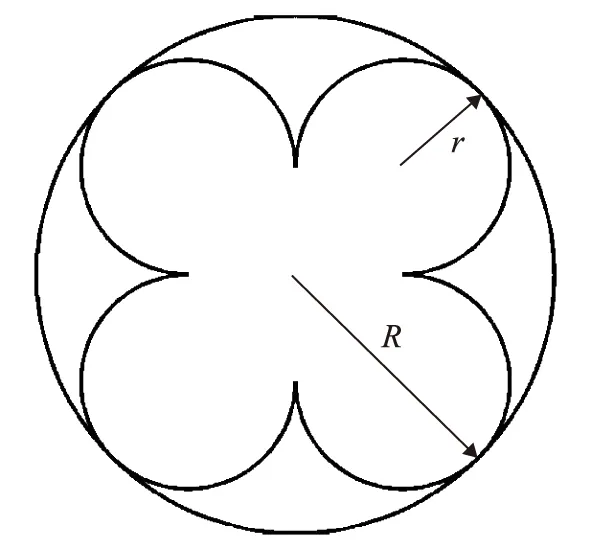
图1 四叶草型催化剂的截面外观

圆柱型催化剂采样点的轴向及径向分布如图2所示。在整个计算过程中定义的权函数支持域尺寸为2。对于半径为2 mm、长度为10 mm的圆柱型催化剂的计算，分别在圆柱体的径向取6个采样点、平面角方向取20个采样点、轴向取41个采样点。

图2 圆柱型催化剂的采样点及计算点分布●—采样点； ●—计算点。 图3同

四叶草型催化剂的截面外观相对复杂，对称性远较圆柱型催化剂差，在径向平面上具有更为丰富的信息。四叶草型催化剂采样点轴向及径向分布如图3所示。在整个计算过程中定义的权函数支持域尺寸为2。对于大圆半径为2 mm、长度为10 mm的四叶草型催化剂的计算，分别在径向取6个采样点、径向平面角方向取40个采样点、轴向取41个采样点。

图3 四叶草型催化剂的采样点及计算点分布

整个计算过程以外界温度370 ℃作为边界条件，通过计算获得热点均匀分布[14]的不同形状催化剂的温度空间分布情况。

1.5 计算体系

采用分布式计算系统对模型进行计算，整套设备包含常规处理器计算机5台，共160个核心。计算体系由24口交换机完成计算数据的传输和交互[15-16]。整个无网格计算过程在本质上具有较好的并发性，采样点对应的形函数及其偏导数的计算以及力矩阵及载荷矩阵的计算组装过程均采用多机并行方式实现，由体系的160个核心并行参与。

2 结果与讨论

采用上述模型对不同反应工况及催化剂尺寸条件下热点分布均匀的圆柱型及四叶草型催化剂在外表面温度为370 ℃时的内部温度分布进行计算，所得催化剂体系内部的最高温度、平均温度以及温度分布的标准差见表1。根据圆柱型催化剂在工况7下的三维温度场分布绘制二维轴向及径向截面图，如图4所示；根据四叶草型催化剂在工况15下的三维温度场分布绘制二维轴向及径向截面图，如图5所示。

2.1 圆柱型催化剂内部温度场分析

由表1可知：裂化反应的放热量、原料密度、反应空速及催化剂半径和长度均影响圆柱型催化剂的内部温度分布；催化剂颗粒内部最高温度及平均温度均随反应放热量、原料密度、反应空速以及催化剂半径、催化剂轴向长度的增加而增大；反应放热量及催化剂颗粒半径对催化剂最高温度及平均温度的影响显著大于催化剂长度、反应空速及原料密度。

对于热点分布均匀的等温反应条件，虽然不同计算工况对应的最高温度及平均温度数值有所不同，但温度分布形式基本类似。由图4可知，圆柱型催化剂内部温度分布的等势面在径向上是严格的圆型分布，在轴向剖面上近似椭圆分布，催化剂外表面温度为370 ℃，由外到内温度逐渐增加，其径向温度梯度大于轴向温度梯度，在圆柱型催化剂的几何中心处温度最高。因此，可以认为虽然在理论上圆柱型催化剂内部并非等温环境，但其内部的反应环境与等温环境类似。而当催化剂半径及长度较大时，催化剂圆柱体中心的最高温度与表面温度相差较大，其反应环境相对于等温反应偏离较大。因此，仅从热效应上考虑，制备圆柱型催化剂时，其半径及长度不宜过大。

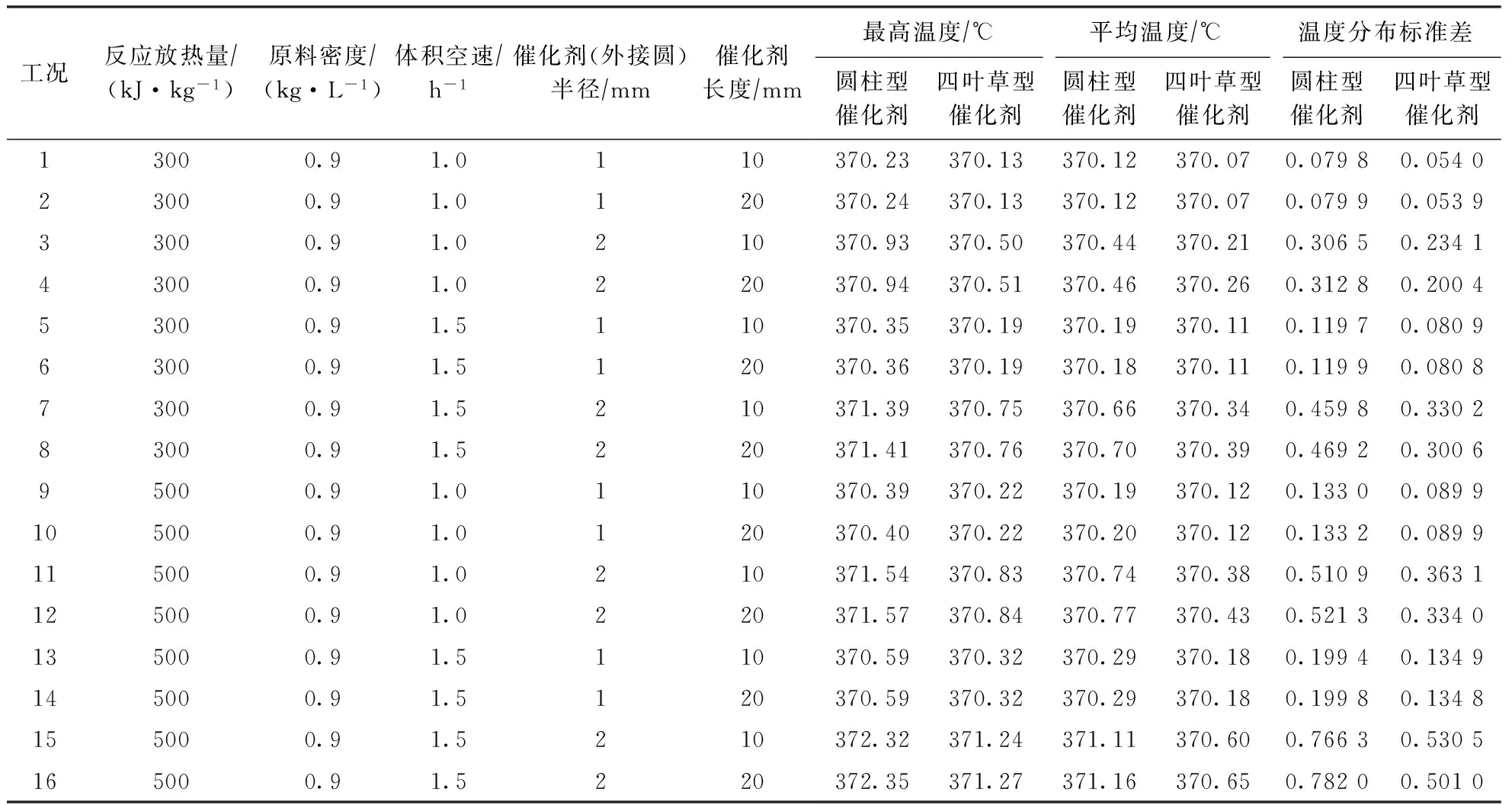
表1 圆柱型及四叶草型催化剂的内部温度分布

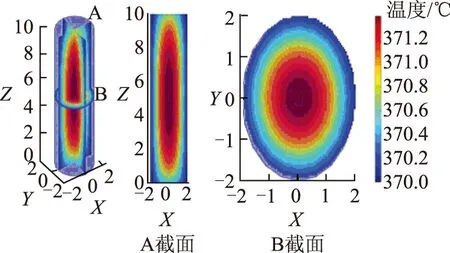
图4 圆柱型催化剂在工况7下的内部温度分布截面图

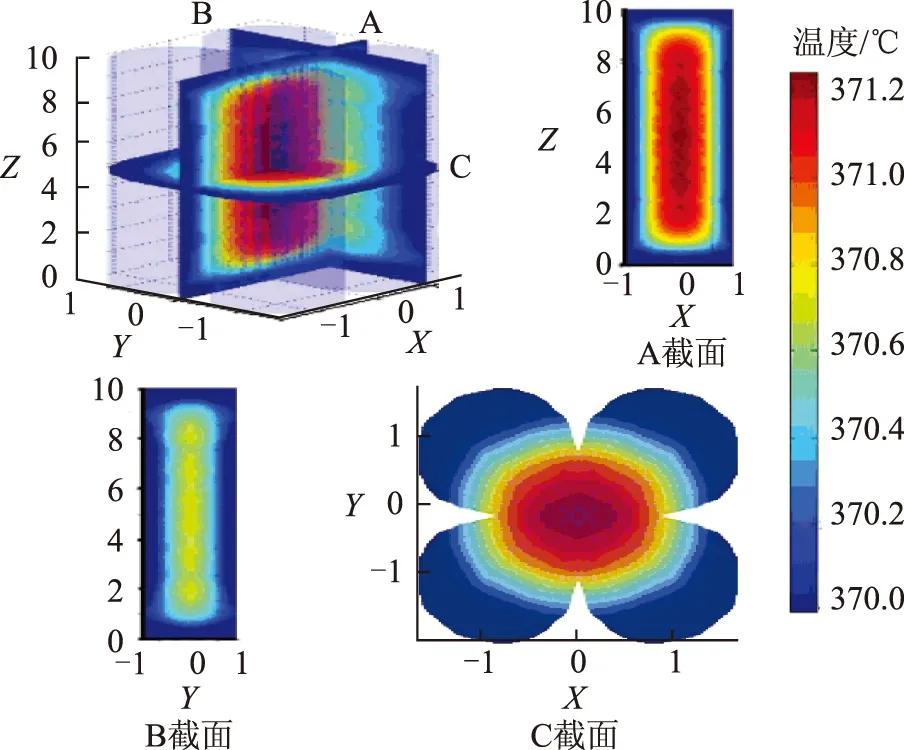
图5 四叶草型催化剂在工况15下的内部温度分布截面图

2.2 四叶草型催化剂内部温度场分析

由表1可知：与圆柱型催化剂相似，裂化反应的放热量、原料密度、反应空速以及催化剂半径均影响四叶草型催化剂内部的温度分布；催化剂颗粒内部的最高温度及平均温度均随反应放热量、原料密度、反应空速、催化剂外接大圆半径以及催化剂长度的增加而增大；反应放热量及催化剂颗粒外接大圆半径对催化剂最高温度及平均温度的影响显著大于催化剂长度、反应空速及原料密度。

通过对比圆柱型和四叶草型催化剂的内部温度分布数据可知，在所有工况条件及催化剂半径和长度均相同时，四叶草型催化剂内部的最高温度及平均温度均低于圆柱型催化剂，两者温度一般相差0.1～0.9 ℃，且四叶草型催化剂内部温度的波动范围小于相应的圆柱型催化剂。

不同工况下四叶草型催化剂内部的温度分布比较相似。在热点分布均匀的等温反应条件下，四叶草型催化剂的截面较圆柱型催化剂复杂，其内部的温度分布形式也与圆柱型催化剂相差较大，尤其体现出了较为复杂的截面温度分布信息。由图5可知，四叶草型催化剂温度分布的等势面在截面每个叶上的径向方向近似呈贝壳型分布，沿催化剂对应的大圆圆心与小圆圆心连线方向的温度梯度变化最小，沿大圆圆心与小圆公切点方向的温度梯度变化最大，由于催化剂体系有对称的特征，最高温度区域与圆柱型催化剂相似，仍在催化剂的中心轴线的中点位置。在轴向剖面上，其温度等势面呈近似圆角矩形分布，催化剂的外表面温度为370 ℃，由外到内温度逐渐增加，其径向的温度梯度大于轴向的温度梯度。因此，同样认为虽然四叶草型催化剂的内部并非等温环境，但其内部的反应环境与等温环境类似。与圆柱型催化剂相似，当四叶草型催化剂外接大圆半径及长度较大时，催化剂中心的最高温度与表面温度相差较大，其反应环境相对于等温反应偏离较大。另外，由于计算机硬件系统内存的限制，沿着大圆圆心与小圆公切点方向及其邻域的计算点与采样点数目有限，导致对该方向及其邻域内温度变化的描述具有一定的误差。

3 结 论

在加氢裂化反应中，圆柱型及四叶草型催化剂颗粒内部的最高温度及平均温度均随反应放热量、空速、原料密度、催化剂半径及催化剂长度的增加而增大，其中反应放热量和催化剂半径对催化剂内部温度的影响更显著。即使在理想的宏观等温反应条件下，两种催化剂内部仍然是非等温区域。在工况条件及催化剂半径和长度均相同时，四叶草型催化剂内部的最高温度、平均温度均低于圆柱型催化剂，具有比圆柱型催化剂更均匀的温度分布。

[1] 尹兆林.炼油企业全厂用能分析及节能优化[J].石油炼制与化工，2012，43(10)：86-91

[2] 董兆海，袁永新，王明传.加氢裂化装置能耗及节能分析[J].齐鲁石油化工，2011，39(2)：87-91

[3] 刘小波，毛羽，王娟，等.基于多孔介质加氢裂化反应器多相流数值模拟[J].石油学报(石油加工)，2012，28(2)：260-267

[4] 龙军，邵潜，贺振富，等.规整结构催化剂及反应器研究进展[J].化工进展，2004，23(9)：925-931

[5] 梁文杰，阙国和.石油化学[M].2版.东营：中国石油大学出版社，2011：356

[6] 郑忠，何腊梅.红外测温技术及在钢铁生产中的应用[J].工业加热，2005，34(3)：25-29

[7] 廖玉麟.数学物理方程[M].上海：华东理工大学出版社，1995：12-13

[8] 吴建民，张海涛，应卫勇，等.钴基催化剂固定床有效导热系数[J].过程工程学报，2010，10(1)：29-34

[9] 刘桂荣，顾元通.无网格法理论及程序设计[M].济南：山东大学出版社，2007：24

[10]刘欣.无网格方法[M].北京：科学出版社，2011：9

[11]贝新源，岳宗五.三维SPH程序及其在斜高速碰撞问题中的应用[J].计算物理，1997，14(2)：155-166

[12]张雄，刘岩.无网格方法[M].北京，清华大学出版社，2001：42

[13]钟万勰.弹性力学求解新体系[M].大连：大连理工大学出版社，1995：35

[14]莫尔比代利M，加夫里迪斯A，瓦尔马A.催化剂设计[M].王安杰，李翔，赵蓓，等，译.北京：化学工业出版社，2004：128

[15]王晓丹，吴崇明.基于MATLAB的系统分析与设计[M].西安：西安电子科技大学出版社，2000：125

[16]刘维.实战Matlab之并行程序设计[M].北京：北京航空航天大学出版社，2012：135-137

NUMERICAL SIMULATION OF TEMPERATURE DISTRIBUTION IN FOUR-LEAF SHAPE CATALYST BY MESHLESS METHOD

Wang Kuo1， Zhao Bo2， Qin Bo1， Du Yanze1

(1.SINOPECFushunResearchInstituteofpetroleumandPetrochemical，Fushun，Liaoning113001； 2.LiaoningShihuaUniversity，CollegeofScience)

Based on three-dimensional bulk of real four-leaf type hydrocracking catalyst， the meshfree calculation to solve the fourier partial differential equation for heat transmission was used to simulate the influence of external temperature fluctuation on the internal temperature distribution in the catalyst using industrial operating temperature and catalysts size as the boundary conditions. The analysis results show that the reactions in the catalyst do not occur under real isothermal surroundings. The maximum and average temperature increases in the cylindrical and four-leaf type catalyst as the increase of reaction heat release， space velocity， feed density， catalyst radius and length of the catalyst. Among them， the heat release and catalyst radius have much more influence. Even under ideal apparent isothermal reaction conditions， the non-isothermal area still exists in the two catalysts. When the operation conditions and catalyst size are the same， the four-leaf type catalyst has the highest internal temperature， while its average temperature and distribution are lower and better than cylindrical one.

hydrocracking catalyst； heat transmission； meshless method； numerical simulation； temperature distribution

2016-02-29； 修改稿收到日期： 2016-05-18。

王阔，硕士，工程师，研究方向为工业催化及分子模拟。

王阔，E-mail：wangkuo.fshy@sinopec.com。

中国石油化工股份有限公司项目(JQ-011308)。