逆向供应链的非合作代价分析①

马祖军， 叶郁森， 代　颖

(1. 西南交通大学经济管理学院物流与应急管理研究所， 成都 610031；

2. 西南交通大学交通运输与物流学院， 成都 610031)



逆向供应链的非合作代价分析①

马祖军1， 叶郁森2， 代颖1

(1. 西南交通大学经济管理学院物流与应急管理研究所， 成都 610031；

2. 西南交通大学交通运输与物流学院， 成都 610031)

摘要：为衡量基于价格合同的逆向供应链运作效率，将非合作代价(PoA)概念引入逆向供应链.考虑废旧产品供应的不确定性，分析了推式和拉式两种结构的两级和多级逆向供应链在分散决策时效率损失的上界.研究表明，逆向供应链并非正向供应链的简单逆过程，这是由于逆向供应链的不确定性主要来自上游端，从而需要考虑废旧产品供应不足导致的缺货风险；推式与拉式两种结构下具有一致的PoA，即分散决策下的效率损失与谁来承担风险无关.此外，逆向供应链级数的递增会加剧供应链效率损失，但逆向供应链级数一定时PoA趋于定值.

关键词：逆向供应链； 效率损失； 非合作代价； 双重边际效应

0引言

随着资源和环境问题日益严重，以资源再生利用、物料增值和成本节约为目的的逆向供应链(reverse supply chain)受到了社会各界的广泛关注.为此，许多学者从不同角度研究了逆向供应链决策问题[1-5]，但不争的事实是，在分散决策下供应链上各主体的“自利”行为将产生双重边际效应(double marginalization)，从而导致供应链效率损失[6,7]，尤其是采用价格合同(price-only contracts)情形.尽管采用复杂的契约进行协调是减少供应链效率损失的重要途径[8,9]，但这些复杂契约的实施具有较高的谈判成本和道德风险，而价格合同由于简单易用，且管理成本低，因而在实际运营管理中仍被广泛采用[10].那么，能否确定出基于价格合同的供应链在分散决策下的效率损失上界，从而准确地衡量其双重边际效应呢？

Koutsoupias和Papadimitriou[11]在研究由于用户的非合作行为而导致整个系统出现效率损失时，提出了非合作代价(price of anarchy，PoA)的概念.PoA问题的研究对非合作系统的效率分析和政策设计有重要价值，近年来已成为交通网络、网络资源分配、网络定价等领域的研究热点.Perakis和Roels[10]首次将PoA概念引入供应链领域，并将其定义为集中决策供应链与分散决策供应链在最差均衡下的收益比.在此基础上，研究了需求函数具有递增广义失效率(increasing generalized failure rate，IGFR)时，多种不同供应链结构下制造商和零售商基于价格合同进行分散决策时的效率损失.之后，Du等[12]考虑需求函数为已知区间上的任意随机分布但不具有IGFR性质，分析了推式供应链结构下的PoA值，结果表明价格合同在需求不确定性较低时可以保证供应链效率.刘天亮等[13]假设需求函数是凸的、需求弹性是关于销售价格的非减函数，基于PoA概念研究了分权供应链在运作效率和社会福利方面的损失问题.

对于两级的正向供应链，在销售价格固定、随机需求的情形下，双重边际效应导致供应链效率损失上界的极小值约为42%[10].而在逆向供应链中，废旧产品在供应时间、数量、质量上的多重不确定性可能使问题变得更复杂[14].然而，目前尚未发现针对逆向供应链中PoA的研究.人们不禁要问：逆向供应链只是正向供应链的简单逆过程吗？如何量化逆向供应链在分散决策下的效率损失？逆向供应链中双重边际效应的强度如何？

为此，本文在文献[10]的基础上，首次将PoA概念引入逆向供应链.针对采用价格合同的逆向供应链，考虑回收市场上废旧产品供应的不确定性，通过PoA值的计算分别确定了推式和拉式两种结构的两级和多级逆向供应链在分散决策时效率损失的上界，并通过数值分析对所得结论进行了验证，从而定量分析了双重边际效应对逆向供应链的影响程度.

1问题描述

考虑图1所示由1个回收商和1个处理商组成的两级逆向供应链系统.设回收商以单位回收价格A向消费者回收某种废旧产品，并以价格w转给专业处理商进行处理.处理商的单位处理成本为c，处理后的再生产品每件售价为p.令r=p-c，表示再生利用单位废旧产品所产生的收益.

图1　逆向供应链系统

在正向供应链中，由于市场供需难以完全匹配，会引发产品库存积压或缺货风险[16].而在逆向供应链中，同样存在供需不匹配的问题：由于在废旧产品供应量尚不明确之前就需要确定废旧产品的计划回收处理量Q，若Q大于市场上的废旧产品供应量R，将导致缺货风险；反之，则会出现回收处理计划不足，造成机会损失.在此假设废旧产品缺货成本为h，而机会损失不计.

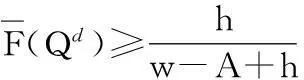
令上标c和d分别表示集中决策与分散决策情形.在分散决策下，逆向供应链上各方均以自身利润最大化为目标，因而最优回收处理量Qd通常不等于Qc，从而引发双重边际效应.在此引入PoA概念，以量化分散决策下逆向供应链效率损失的上界.

定义逆向供应链的PoA是指集中决策与分散决策在最差均衡状态下的收益比，即

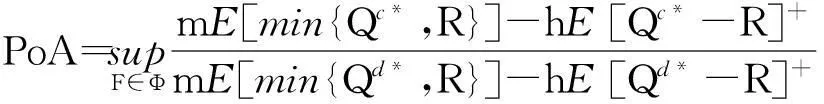
2集中式决策

为衡量分散决策下逆向供应链运作效率损失的上界，首先分析集中决策下逆向供应链的运作效率作为比较基准.

在集中决策下，好似由单一决策者负责整个逆向供应链的运作，使得供应链整体的利润最大化，即目标函数为

(1)

将式(1)对Qc求一阶偏导可得

(2)

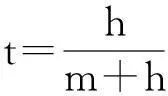
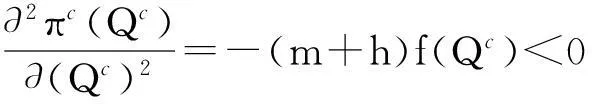
3分散式决策

在分散决策下，逆向供应链成员根据相互间的主从关系在完全信息条件下进行Stackelberg博弈.主导方(leader)提供价格合同给跟从方(follower)，跟从方可选择接受或拒绝(take-it-or-leave-it).据此确定供应链上下游之间废旧产品的交易价格w和最优交易量Qd*.

文献[10]和[16]指出，可根据谁来承担因产品供过于求导致的库存积压风险，将正向供应链结构分为推式和拉式两种类型：由供应链下游方承担产品库存积压风险时，为推式(push)结构；反之为拉式(pull)结构.类似地，逆向供应链也分为推式和拉式结构[17-19]，可根据谁来承担因废旧产品供应不足导致的缺货风险来区分：由供应链下游方承担废旧产品供应缺货风险时，为推式结构；反之为拉式结构.

为此，可将分散决策下两级逆向供应链的Stackelberg博弈过程描述如下(博弈的最后两步取决于推式还是拉式结构)：

1)主导方确定废旧产品交易价格w，并提供该价格合同给跟从方.

2)若跟从方的期望利润大于其底线收益(假设为零)，则接受该价格合同；否则，无法达成交易.

3)处理商拟定废旧产品的计划处理量.

对于推式供应链：

4)废旧产品的供应量R实现.

5)回收商根据废旧产品供应情况确定回收量.若废旧产品供应不足，处理商承担缺货风险；反之，不考虑机会损失.

对于拉式供应链：

4)回收商确定计划回收量.

5)废旧产品的供应量R实现.若废旧产品供应不足，回收商承担缺货风险；反之，不考虑机会损失.

下面分别考虑推式和拉式结构下的逆向供应链决策问题，且先考虑两级逆向供应链情形，之后再扩展到多级逆向供应链情形.

3.1推式逆向供应链

3.1.1回收商主导

当回收商在逆向供应链中占主导地位时，由其决定废旧产品的交易价格w，而处理商则确定废旧产品的计划交易量Qd，并承担废旧产品供应不确定性导致的缺货风险.

处理商的利润函数为

(3)

回收商的利润函数为

(4)

因此，回收商的决策模型为

(5)

采用逆向归纳法求解，将式(3)对Qd求导可得

(6)

将式(6)带入式(4)，再对w求导，整理可得

(7)

命题1在两级推式逆向供应链中，基于价格合同的非合作代价为

PoA=e-1

其中e为自然对数的底数，约等于2.718 282.

3.1.2处理商主导

此时由处理商决定废旧产品的交易价格w，而回收商确定废旧产品的计划交易量Qd.废旧产品供应不确定性导致的缺货风险由处理商承担.

处理商的决策模型为

(8)

由于处理商既是合同主导方，又承担缺货风险，为了规避风险，处理商的最优定价应为w=A.此时，供应链绩效表现与集中决策时一致，即PoA=1.

3.1.3多级推式逆向供应链

现实生活中的废旧产品(如WEEE)回收渠道复杂多样，可能要经过多级回收商交易才能最终到达处理商.为此，考虑回收商主导的多级推式逆向供应链，链上的每一级成员都提供价格合同给其下级成员.为凸显双重边际效应的影响，假设中间商交易既不产生额外成本，亦不增值.

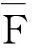
命题2在n级推式逆向供应链中，基于价格合同的非合作代价为

由命题2可知，当n=3时，PoA=3.19；当n=4时，PoA=6.36.

3.2拉式逆向供应链

3.2.1处理商主导

当处理商在逆向供应链中占主导地位时，由其决定废旧产品的交易价格w，而回收商确定废旧产品的计划交易量Q，并承担废旧产品供应不确定性导致的缺货风险.

处理商的利润函数为

(9)

回收商的利润函数为

(10)

因此，处理商的决策模型为

(11)

同理，采用逆向归纳法可求得

(12)

(13)

命题3在两级拉式逆向供应链中，基于价格合同的非合作代价为

PoA=e-1

其中e为自然对数的底数.

3.2.2回收商主导

此时由回收商决定废旧产品的交易价格w，而处理商则确定废旧产品的计划交易量Qd.废旧产品供应不确定性导致的缺货风险由回收商承担.

回收商决策模型为

(14)

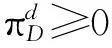
由于回收商既是合同主导方，又承担缺货风险，为规避风险，回收商最优定价应为w=r.供应链绩效表现也与集中决策一致，即PoA=1.

3.2.3多级拉式逆向供应链

类似地，考虑处理商主导的多级拉式逆向供应链情形，供应链上的每一级成员都提供价格合同给其上一级成员.同样假设中间商交易既不产生额外成本，亦不增值.

命题4在n级拉式逆向供应链中，基于价格合同的非合作代价为

3.3推式/拉式逆向供应链的运作效率比较

表1比较了推式和拉式两种结构下逆向供应链的运作效率.

Table 1 Efficiency of reverse supply chains with push or pull configuration

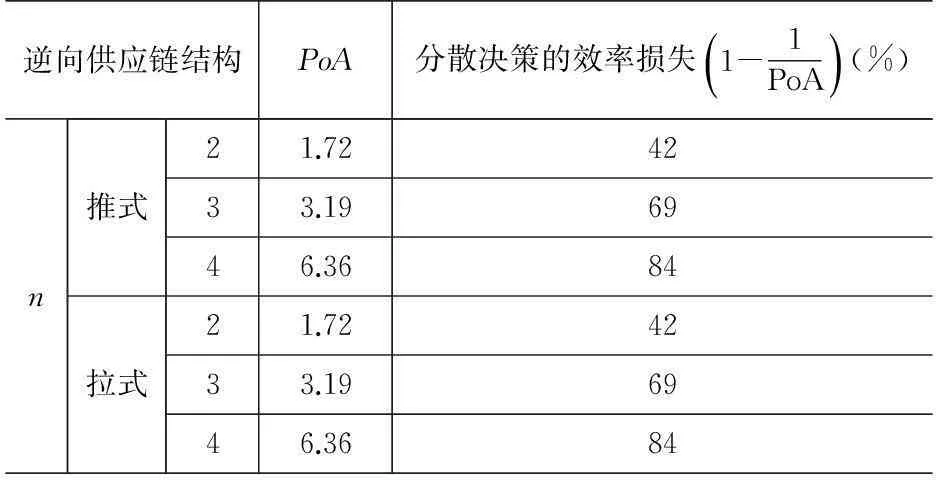
逆向供应链结构PoA分散决策的效率损失1-1PoA()(%)n推式拉式21.724233.196946.368421.724233.196946.3684

可以看出，在逆向供应链中无论是推式还是拉式结构，其非合作代价PoA是一致的.这说明在逆向供应链中，不管由谁来承担废旧产品供应不确定性导致的缺货风险，都不会引起PoA的变化，即两种结构的逆向供应链在分散决策下的效率损失相同.

此外，逆向供应链的PoA在供应链级数一定时趋于定值，与模型中的成本收益参数(如回收价格、边际利润率、缺货成本等)和数量参数(如计划交易量)的取值均无关.但随着中间交易环节的增加，逆向供应链的绩效将越来越差，效率损失呈递增趋势：两级情形为42%，三级情形为69%，四级情形为84%.

4数值分析

表2　Gamma分布随机供应下两级逆向供应链的绩效分析

注： 由于供应链效率与Gamma分布尺度参数λ无关[15]，在此仅调整形状参数α，其取值范围与文献[10]一致.表中各行数值

为α在每个区间随机取值20次计算所得有效值的平均值.可以看出，前文求得的PoA值明显高于Gamma分布随机供应下逆向供应链在集中决策与分散决策下的效益比πc*/πd*(差距范围约在20%～40%之间)，且πc*/πd*随期望回收率1-t的减小而增大，即分散决策下的供应链绩效随之变差.有趣的是，虽然集中决策与分散决策下最优回收处理量的差值是引发双重边际效应的主要原因，但其比值因受到Gamma分布形状参数α的影响，并不一定与πc*/πd*具有相同的变化趋势(例如当α∈(0.5,5)且1-t递减时，πc*/πd*递增，而Qc*/Qd*递减).

表3给出了废旧产品供应服从均匀分布时两级逆向供应链的绩效表现.此时，逆向供应链在集中决策与分散决策下的效益比πc*/πd*也明显小于PoA值(差距范围约在35%～42%之间)，且πc*/πd*也随期望回收率1-t的减小而增大；集中/分散决策下的最优回收处理量之比Qc*/Qd*与πc*/πd*呈同向变化.

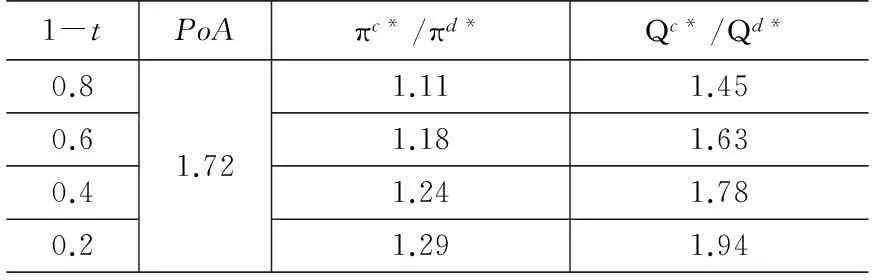
表3　均匀分布随机供应下两级逆向供应链的绩效分析

注： 表中各行数值为参数b在区间(0,100)中随机取值20次

计算所得有效值，结果都一致，即与参数b无关.

图2　不同分布函数随机供应下逆向供应链集中/分散决策的效益比

图2给出了废旧产品供应服从不同随机分布时两级逆向供应链在集中/分散决策下的效益比与PoA值随预计回收率1-t的变化情况(其中Gamma分布是取参数α∈(0.05,0.5)时的计算结果).

5结束语

本文针对基于价格合同的逆向供应链运作效率问题，引入PoA概念，并考虑废旧产品供应不确定性导致的缺货风险，研究了推式和拉式两种结构的逆向供应链在两级和多级情形下由于分散决策所引发的效率损失上界，得到如下结论：

(1)逆向供应链并非正向供应链的简单逆过程，主要表现在：

1)不管是正向供应链，还是逆向供应链，供需不匹配都将导致供应链成员面临一定的风险，但在正向供应链中，源于产品需求的不确定性，导致的是产品库存积压风险或缺货风险；而在逆向供应链中，主要面临废旧产品供应的不确定性，由此引发废旧产品供应不足的缺货风险或供应过剩的机会损失.

2)在正向供应链中，拉式结构与推式结构相比具有较小的效率损失[10].但在逆向供应链中，两种结构均受到废旧产品供应量的约束，具有一致的PoA，即在分散决策下的效率损失相同.

(2)逆向供应链在分散决策下的效率损失不可避免，且随着供应链级数的增加，效率损失呈递增趋势(如两级情形下PoA为1.72，即效率损失为42%；三级情形下PoA为3.19，即效率损失为69%；四级情形下PoA为6.36，即效率损失为84%).但在供应链级数一定时，PoA趋于一个定值.

(3)由于价格合同下的自由市场竞争受到个体利益最大化的驱动，逆向供应链中风险承担方的个体决策(废旧产品回收处理量)在废旧产品供应限制下通常趋于保守，导致市场上可回收的废旧产品得不到充分的回收利用.因此，需要政府对逆向供应链成员给予经济或政策上的扶持与帮助，以实现社会福利最大化.

本文研究的是串行逆向供应链的非合作代价，进一步的研究可考虑更复杂的供应链结构，比如研究单边竞争甚至多边竞争的情形.也可研究闭环供应链的非合作代价，并同时考虑产品需求的不确定性和废旧产品供应的不确定性.此外，还可考虑信息是否对称、不确定性分布为线性或非线性等情形.

参 考 文 献：

[1]Savaskan R C, Bhattacharya S, Van Wassenhove L N. Closed-loop supply chain models with product remanufacturing[J]. Management Science, 2004, 50(2): 239-252.

[2]Savaskan R C, Van Wassenhove L N. Reverse channel design: The case of competing retailers[J]. Management Science, 2006, 52(1): 1-14.

[3]Kaya O. Incentive and production decisions for remanufacturing operations[J]. European Journal of Operational Research, 2010, 201(2): 442-453.

[4]聂佳佳. 零售商信息分享对闭环供应链回收模式的影响[J]. 管理科学学报, 2013, 16(5): 69-82.

Nie Jiajia. Effects of retailer information sharing on collecting modes of closed-loop supply chain[J]. Journal of Management Sciences in China, 2013, 16(5): 69-82. (in Chinese)

[5]黄宗盛, 聂佳佳, 胡培. 基于微分对策的再制造闭环供应链回收渠道选择策略[J]. 管理工程学报, 2013, 27(3): 93-102.

Huang Zongsheng, Nie Jiajia, Hu Pei. Dynamic closed-loop supply chain models with product remanufacturing[J]. Journal of Industrial Engineering /Engineering Management, 2013, 27(3): 93-102. (in Chinese)

[6]黄祖庆, 达庆利. 直线型再制造供应链决策结构的效率分析[J]. 管理科学学报, 2006, 9(4): 51-57.

Huang Zuqing, Da Qingli. Study on efficiency of serial supply chains with remanufacture[J]. Journal of Management Sciences in China, 2006, 9(4): 51-57. (in Chinese)

[7]丁雪峰, 但斌, 张旭梅, 等. 有限产能条件下闭环供应链渠道效率研究[J]. 计算机集成制造系统, 2010, 16(1): 149-154.

Ding Xuefeng, Dan Bin, Zhang Xumei, et al. Research on channel efficiency of closed-loop supply chains under finite capacity[J]. Computer Integrated Manufacturing Systems, 2010, 16(1): 149-154. (in Chinese)

[8]Govindan K, Popiuc M N. Reverse supply chain coordination by revenue sharing contract: A case for the personal computers industry[J]. European Journal of Operational Research, 2014, 233(2): 326-336.

[9]王玉燕. 需求与成本双扰动时闭环供应链的生产策略和协调策略[J]. 系统工程理论与实践, 2013, 33(5): 1149-1157.

Wang Yuyan. Adjusted production strategy and coordination strategy in closed-loop supply chain when demand and cost disruptions[J]. Systems Engineering-Theory & Practice, 2013, 33(5): 1149-1157. (in Chinese)

[10]Perakis G, Roels G. The price of anarchy in supply chains: Quantifying the efficiency of price-only contracts[J]. Management Science, 2007, 53(8): 1249-1268.

[11]Koutsoupias E, Papadimitriou C. Worst-case equilibria[C]// Proceeding of the 16th Symposium on Theoretical Aspects of Computer Science, NCS 1563, 1999: 404-413.

[12]Du D, Chen B, Xu D. Quantifying the efficiency of price-only contracts in push supply chains over demand distributions of known supports[J]. Omega, 2014, 42: 98-108.

[13]刘天亮, 陈剑, 辛春林. 凸需求情形下分权供应链运作效率及福利分析[J]. 管理科学学报, 2011, 14(1): 61-68.

Liu Tianliang, Chen Jian, Xin Chunlin. Analysis on social welfare and operational efficiency in decentralized supply chains with convex demand[J]. Journal of Management Sciences in China, 2011, 14(1): 61-68. (in Chinese)

[14]Daniel V, Guide Jr R, Jayaraman V. Product acquisition management: Current industry practice and a proposed framework[J]. International Journal of Production Research, 2000, 38(16): 3779-3800.

[15]Lariviere M A, Porteus E L. Selling to the newsvendor: An analysis of price-only contracts[J]. Manufacturing Service Operations Management, 2001, 3(4): 293-305.

[16]Cachon G P. The allocation of inventory risk in a supply chain: Push, pull and advance-purchase discount contracts[J]. Management Science, 2004, 50(2): 222-238.

[17]Fleischmann M, van Nunen J, Gräve B, et al. Reverse Logistics-Capturing Value in the Extended Supply Chain[M]//An C, Fromm H. (Eds), Supply Chain Management on Demand, Springer, 2005: 167-186.

[18]Fleischmann M, van Nunen J, Grave B. Integrating closed-loop supply chains and spare-parts management at IBM[J]. Interfaces, 2003, 33(6): 44-56.

[19]Umeda S. Performance Analysis of Reverse Supply Chain Systems by Using Simulation[M]// Prabhu V, Taisch M, Kiritsis D. (Eds), Advances in Production Management Systems, Springer, 2013: 134-141.

附录

命题1的证明

(A1)

其中α→0.

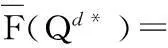
(A2)

根据定义有

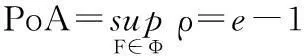
命题1得证.

引理1的证明

当n=2时，即两级情形，前文已证明满足.

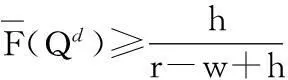
引理1得证.

命题2的证明

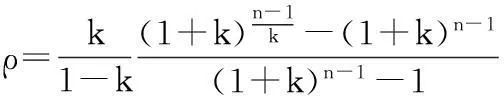
命题2得证.

命题3的证明

根据定义有

命题3得证.

引理2的证明

当n=2时，即两级情形，前文已证明满足.

引理2得证.

命题4的证明

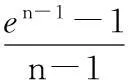
命题4得证.

Quantifying the price of anarchy in reverse supply chains

MAZu-jun1,YEYu-sen2,DAIYing1

1. Institute for Logistics and Emergency Management, School of Economics and Management, Southwest Jiaotong University, Chengdu 610031, China;2. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 610031, China

Abstract:The price of anarchy (PoA) is introduced to quantify the efficiency of reverse supply chains that use price-only contracts. Considering the uncertainty existing in the supply of used products, the upper bounds of efficiency losses in a decentralized reverse supply chain are derived for different configurations: push or pull with two or more stages. The results show that a reverse supply chain is not just the reverse of a forward supply chain, because the uncertainty in a reverse supply chain comes mainly from the supply side, and it is necessary to take into account the out-of-stock risk due to the insufficient supply of used products. The PoA in a decentralized supply chain proves to be constant for both push and pull configurations. That is, who bears the risk has no effect on the loss of efficiency. Besides, the efficiency generally drops with the number of intermediaries in a reverse supply chain. For a reverse supply chain with fixed stages, however, the value of PoA turns out to be constant.

Key words:reverse supply chain; loss of efficiency; price of anarchy; double marginalization

中图分类号:F252

文献标识码:A

文章编号:1007-9807(2016)02-0066-08

作者简介:马祖军(1974—)， 男， 浙江开化人， 博士， 教授， 博士生导师. Email: zjma@swjtu.edu.cn

基金项目：国家自然科学青年基金资助项目(71103149)； 国家自然科学基金重大资助项目(71490722)； 教育部新世纪优秀人才支持计划资助项目(NCET-10-0706).

收稿日期：① 2013-07-02；

修订日期:2014-12-27.