基于混合量测的二次线性状态估计方法及其工程应用
丁宏恩,戴则梅,霍雪松,周劼英,徐秀之,吕 洋,俞 瑜
基于混合量测的二次线性状态估计方法及其工程应用
丁宏恩1,戴则梅2,霍雪松3,周劼英4,徐秀之1,吕 洋1,俞 瑜1
(1.国网苏州供电公司,江苏 苏州 215004;2.南瑞集团公司(国网电力科学研究院),江苏 南京 211106;3.国网江苏省电力公司,江苏 南京 210024;4.国家电力调度控制中心,北京 100031)
基于相量测量单元(PMU)和数据采集与监控(SCADA)混合量测进行状态估计计算时,如果仍采用传统非线性估计模型,将面临PMU量测计算权值难以确定、PMU量测坏数据辨识不准、相角参考点和成熟商用程序改动等多方面问题。提出了一种基于混合量测的二次线性状态估计方法。该方法在传统非线性状态估计收敛后,利用其结果中的各节点电压幅值及相角估计值和PMU相量量测再进行二次线性状态估计计算,有效解决了上述问题。最后结合电网实例验证了该方法的有效性。
状态估计;PMU量测;坏数据处理;计算权值;相角参考点
0 引言
状态估计是电网调度自动化系统的基础应用,其主要功能是从含有误差的电力系统实时数据中获得系统状态信息的最佳估计值[1-2]。随着电网调度自动化水平的不断提高和新型智能电网调度控制系统的广泛应用[3-4],作为电力系统实时在线分析的基础,状态估计应用的重要性被提到了一个更新的高度[5-6]。传统状态估计使用的实时数据主要由监控和数据采集(SCADA)应用提供,近年来,利用电网广域动态监视(WAMS)应用提供的高精度相量测量装置(PMU)量测在改善状态估计性能方面取得了不少成果[7-9]。现阶段我国电网中配置的PMU数目远不足以进行完全基于PMU量测的状态估计,一种比较可行的方案是基于PMU量测和SCADA混合量测进行状态估计。
将高精度PMU相量量测直接或者适当变换后引入到传统非线性状态估计中,可以增大量测系统冗余度,提高状态估计的性能[10-11]。但是传统引入方法并没有充分利用PMU量测高精度、直接可测相角以及状态量线性等特性,大多仍采用非线性估计模型,将PMU相量量测和传统SCADA量测等同对待,将二者混合在一起进行非线性迭代计算和坏数据处理[11-14],这样的混合处理将带来PMU量测计算权值确定、PMU量测坏数据处理、相角参考点等一系列不易克服的问题。
本文另辟蹊径提出了一种基于混合量测的二次线性状态估计方法。该方法在传统非线性状态估计收敛以后,利用其结果(各节点电压幅值及相角估计值)和PMU相量量测再进行二次线性状态估计计算,几乎不对原有工程化程序进行任何改动,就可以很方便地解决上述问题,极大地推动了混合量测状态估计的实用化。
1 二次线性状态估计模型
WAMS能够提供的PMU相量量测主要包括节点电压相量量测和支路电流相量量测。其中,PMU节点电压相量量测可以在二次线性状态估计中直接使用,PMU支路电流相量量测需要按照以下方法转化为相邻节点电压相量量测以后使用[15-16]。
基于PMU节点电压相量量测和相关支路PMU电流相量量测,可以推算出相邻未装置PMU节点的电压相量量测[17-18]。以图1所示的单支路图为例,假设在节点1配置PMU,,为PMU相量测量,如式(1)所示,可以利用和推算出相邻未装置PMU节点2的电压相量量测。这些节点电压相量量测和PMU节点电压相量量测一样可以在二次线性状态估计中直接使用。
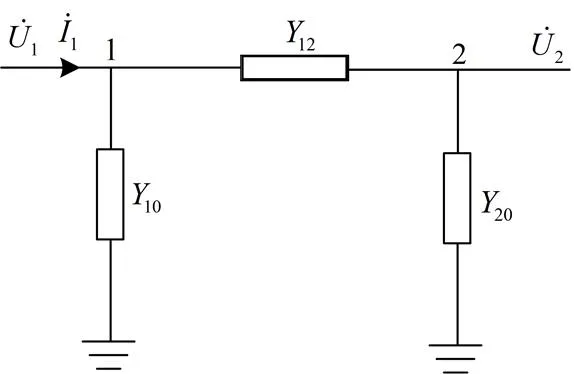
图1 单支路图
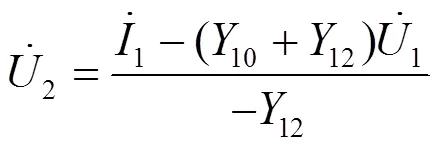
传统非线性状态估计收敛以后,利用其结果中的各节点电压幅值及相角估计值和PMU相量量测再进行二次线性状态估计计算在二次线性状态估计可使用的量测包括:PMU节点电压相量量测(其中包含转化来的相邻节点电压相量量测)、传统非线性状态估计结果,所有量测值与节点状态量均存在直接的线性关系,因而计算可在极坐标下进行且有功和无功可以分解计算。以有功部分为例,其量测方程为如式(2)所示。
(2)
分析上述量测方程会发现,所有量测皆为节点状态量测,关系矩阵与系统拓扑及参数没有关系,每行只含有非零元素1,始终不变且高度稀疏,这些特点都大大减小了线性状态估计的计算量。根据上面的量测方程,应用加权最小二乘法原理可以得到线性状态估计的计算式如式(3)所示。

式中,1为量测的计算权值矩阵。
有功部分二次线性状态估计计算程序流程如图2所示。

图2 计算程序流程图
2 若干问题的处理方法
应用本文方法将PMU量测引入状态估计时,可以很方便地解决传统引入方法所面临的PMU量测计算权值确定、PMU量测坏数据处理、相角参考点三大问题,以下将分别详述。
2.1 PMU量测计算权值确定
采用传统非线性估计模型引入PMU量测,不考虑PMU量测的特殊性,将PMU相角量测和传统SCADA量测等同对待,将与系统状态量成非线性关系的传统SCADA量测中的发电机、变压器、线路等功率量测和与系统节点状态量成线性关系的PMU电压相量量测混合在一起进行非线性迭代计算,不同特性的量测直接混合在一起计算,怎样给新增的PMU量测一个合适的计算权值成为了问题。
本文所述的二次线性状态估计方法为确定PMU量测计算权值提供了新思路。二次计算时所有量测值与节点状态量均存在直接的线性关系,可以很方便很直观地给新增的PMU量测确定一个合适的计算权值。
首先,确定PMU电压相量量测计算权值的方法,类似于其他常规类型量测,第个PMU电压相量量测的计算权值如式(4)所示[1]。

其次,还必须确定传统非线性状态估计结果相量的计算权值。传统非线性状态估计结果相量的计算权值同样也跟其误差的方差有关,因此求解传统非线性状态估计的结果相量计算权值的关键点是如何求解其误差的方差矩阵。已知传统非线性状态估计的所有SCADA量测误差的方差矩阵如式(5)所示。

依据参考文献[2],不难推导出传统非线性状态估计的结果相量误差的方差矩阵如式(6)所示。该式即为基于传统非线性状态估计SCADA量测误差的方差矩阵求解其结果相量误差的方差矩阵的关系式。
(6)
如果传统非线性估计一般采用快速分解法,仿照式(6)同样可以推导出快速解耦法非线性状态估计结果相量误差的方差矩阵和,分别如式(7)和式(8)所示。

(8)
2.2 PMU量测坏数据处理
采用传统非线性估计模型引入PMU量测,不考虑PMU量测的特殊性,将PMU相角量测和传统SCADA量测等同对待,将与系统状态量成非线性关系的传统SCADA量测中的发电机、变压器、线路等功率量测和与系统节点状态量成线性关系的PMU电压相量量测混合在一起坏数据处理,造成了PMU量测坏数据检测辨识不准确。
基于残差搜索辨识法[2]基本原理的启发,考虑到基于传统非线性状态估计结果相量和PMU电压相量量测的二次线性状态估计计算量非常小且可以快速多次重复计算的特点,本文提出在二次线性状态估计中使用经过改进的最大标准化残差搜索法处理PMU电压相量量测坏数据。
以有功部分为例,第个PMU电压相角量测的标准化残差如式(9)所示。

(10)
二次线性状态估计量测坏数据处理程序的具体流程如图3所示。
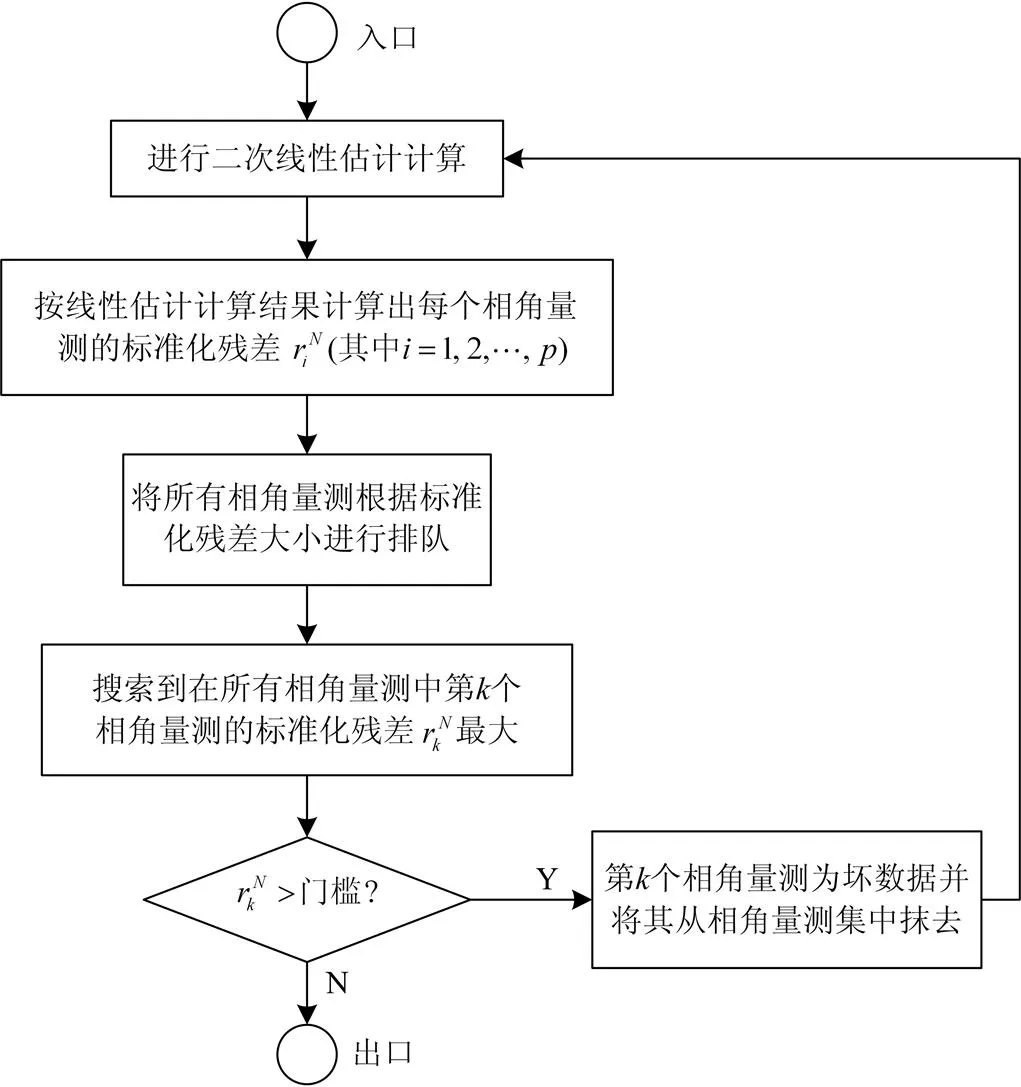
图3 坏数据处理程序流程图
2.3 相角参考点问题
采用传统非线性估计模型引入PMU量测时,在形成雅克比矩阵时,并不考虑PMU量测的特殊性,作为角度的唯一参考的相角参考点状态量对应列仍然不建立,且不参与迭代求解,不能计算相角参考点上角度量测的残差值,故而参考点上相角量测坏数据无法通过量测残差搜索方法辨识出来。同时,由于实际WAMS所提供的PMU电压相角量测都是基于一个相角参考点的相角量测差,引入计算时,一旦相角参考点上PMU电压相角量测为坏数据,将影响其余所有相角量测的引入,污染全系统有功量的总体计算,严重影响状态估计精度。
基于混合量测的二次线性状态估计方法,本文提出一种解决相角参考点坏数据问题的新方法,在进行二次线性状态估计时改变传统状态估计将相角参考点状态量值固定且不参与迭代求解的做法,形成关系矩阵时增加相角参考点状态量对应列和PMU量测对应行,将相角参考点状态量同其他节点一样参与迭代求解,能够使相角参考点上的PMU电压相角量测为坏数据时同样能够被检测和辨识,使其不会影响其余相角量测的引用,彻底消除其对计算结果的不利影响。处理模块的相关环节包括:
(1) 读取WAMS系统中相角参考母线信息;
(2) 将WAMS系统的相角参考母线作为二次线性状态估计的相角参考点,统一PMU相角量测和状态估计的相角参考点;
(3) 基于二次线性状态估计模型,形成关系矩阵时增加被传统状态估计排除在外的与相角参考点相对应的列,将相角参考母线的状态量同其他母线的状态量一样参与计算求解;
(4) 将相角参考点的PMU电压相角量测参与量测的坏数据处理。
具体增加的程序流程如图4所示。
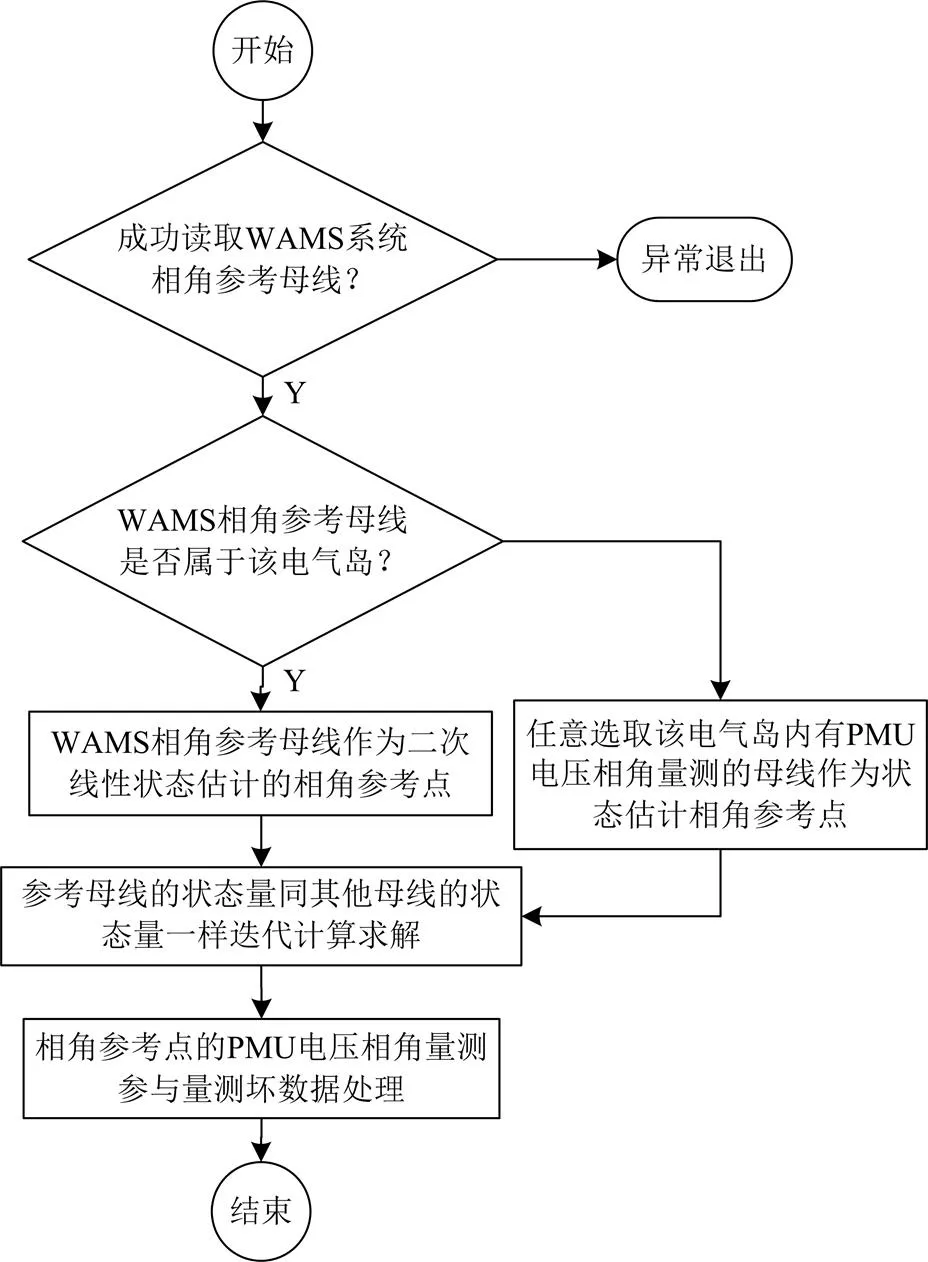
图4 相角参考点处理模块的程序流程
3 实例验证
(1) 计算网络
选取某省级真实电网的部分区域作为计算网络,计算节点数为728,量测系统中有功SCADA量测约为2 561个,PMU母线电压相角量测约为36个。其中由于新海站PMU子站GPS失步,新海220 kV正母线上的PMU电压相角量测置为坏数据。
(2) 试验算法
以有功计算为例,基于传统非线性状态估计结果中电压相角和PMU电压相角量测进行二次线性状态估计计算。
(3) 估计精度指标
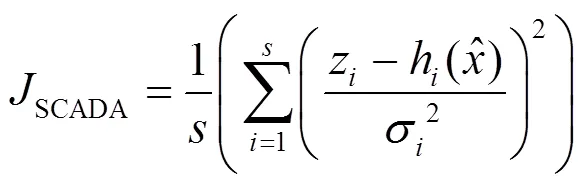
式中:为SCADA有功量测总数;h()为量测相对于状态矢量的非线性函数。
式中,为母线电压相角量测总数。
(4) 二次线性状态估计相角计算权值
非线性状态估计结果相角的计算权值取为SE(SE=,为非线性状态估计结果相角误差统一的标准差);
PMU母线电压相角量测的计算权值取为PMU(PMU=,为PMU电压相角量测误差统一的标准差)。
(5) 计算权值确定
基于15个不同时间段的量测数据断面,在不同计算权值条件下运行本文算法程序,估计精度量化指标和的计算值如表1所示。
(6) 相角参考点和坏数据问题处理
设置新海220 kV正母线作为基于混合量测二次线性状态估计的相角参考点。然后基于某个数据断面,应用不处理相角参考点及坏数据问题的传统非线性状态估计方法(以下简称算法1)和本文处理相角参考点及坏数据问题的二次线性状态估计方法(以下简称算法2)分别计算一次,两种算法结果的比较如表2所示,表2全部内容详见附录A表A1。表2中误差比为量测和估计结果的误差百分比,基值为360º。
(7) 试验结论
a) 表1某些数据断面时,如数据断面1、3、6、8、9、12和14,在PMU电压相角量测的计算权值取较小的条件下(当SE/PMU==100时),引入PMU电压相角量测可以使得基于混合量测运行状态估计时的与仅用SCADA量测进行状态估计时的相比变小,首先证明只要给现在实际工程中的PMU电压相角量测相对合适的计算权值,引入后便可以改善状态估计精度;其次能够证明更重要一点,现在实际工程中的PMU电压相角量测误差的标准差大约是传统非线性状态估计结果相角误差的标准差的10倍,这个结论解决了PMU电压相角量测计算权值的确定问题。
b) 表1在所有数据断面时,在PMU电压相角量测的计算权值取较大的条件下(当SE/PMU=时),引入PMU电压相角量测使得基于混合量测运行状态估计时的与仅用SCADA量测进行状态估计时的相比变大明显,本文方法试验数据能够证明现在实际工程中的PMU电压相角量测精度还没有达到可以设置很大计算权值参与状态估计的标准,显然离用它们直接代替状态估计结果的标准更远。
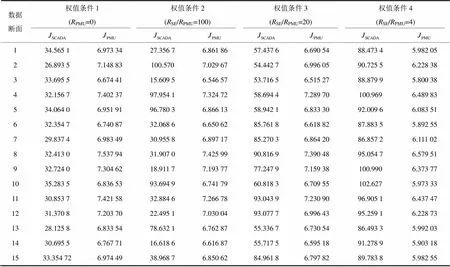
表1 试验数据统计表

表2 典型PMU相角量测值和估计结果对比表
c) 分析表2中数据可知,当采用本文方法处理相角参考点及坏数据问题时,相角参考点上的PMU相角量测为坏数据但被正确辨识出来,如表2中算法2结果所示,在相角参考点上,正确判出坏数据数目为两个,完全没有影响其余相角量测的引入,相角参考点上的相角量测坏数据没有影响状态估计精度。
d) 分析表2中数据可知,本文提出的改进最大标准化残差搜索法能够准确有效地将PMU电压相量量测中坏数据检测辨识出来。
4 结语
本文提出了一种基于混合量测的二次线性状态估计方法,使得PMU量测对状态估计精度的影响更加直观,且在PMU量测计算权值确定、PMU量测坏数据处理、相角参考点等问题的解决上极具优势。算法的实现也不需要对传统非线性状态估计做任何改动,只需增加一些自身模块,易于实用化推广,具有良好的应用前景。
附录A
表A1 全部PMU相角量测值和估计结果对比表
TableA1 Results statistics of all PMU measurements

母线上的PMU电压相角量测量测值算法1结果算法2结果 估计结果误差比坏数据估计结果误差比坏数据 新海220 kV正母0.000.000.00否61.2717.02是 新海220 kV副母-0.120.000.03否61.2717.05是 东善桥500 kV I段母63.012.1416.91是61.850.32否 东善桥500 kV II段母63.012.1416.91是61.850.32否 东善桥220 kV I段母61.170.7116.80是60.380.22否 东善桥220 kV II段母61.170.7116.80是60.380.22否 东善桥220 kV III段母61.170.7116.80是60.380.22否 东善桥220 kV IV段母61.170.7116.80是60.380.22否
续表A1

母线上的PMU电压相角量测量测值算法1结果算法2结果 估计结果误差比坏数据估计结果误差比坏数据 华润南220 kV I段母62.171.4416.87是61.120.29否 石牌500 kV I段母52.58-8.2716.90是51.120.38否 石牌500 kV II段母52.58-8.2716.90是51.120.38否 石牌220 kV I段母49.17-11.2716.79是48.160.28否 石牌220 kV II段母49.17-11.2716.79是48.160.28否 石牌220 kV III段母49.17-11.2716.79是48.160.28否 石牌220 kV IV段母49.17-11.2716.79是48.160.28否 环保220 kV正母50.42-10.1916.84是49.220.33否 环保220 kV副母50.42-10.1916.84是49.220.33否 斗山220 kV I段母52.03-7.6516.58是50.740.36否 斗山220 kV II段母52.04-7.6516.58是50.740.36否 斗山220 kV III段母52.03-7.6516.58是50.740.36否 利港二500 kV I段母55.00-5.7816.88是53.520.41否 利港二500 kV II段母55.00-5.7816.88是53.520.41否 扬二厂500 kV I段母66.515.5816.93是65.380.32否 扬二厂500 kV II段母66.515.5816.93是65.380.32否 华通220 kV正母55.22-5.3916.84是54.240.27否 华通220 kV副母55.25-5.3916.84是54.240.28否 天厂220 kV正母55.94-4.8416.88是54.760.33否 天厂220 kV副母55.94-4.8416.88是54.760.33否 彭城220 kV副母72.7011.4917.00是71.660.29否 彭城220 kV正母72.6711.4917.00是71.660.28否 徐厂220 kV I段母66.505.3216.99是65.600.25否 徐塘220 kV I段母64.693.2517.07是63.700.27否 徐塘220 kV II段母64.703.2717.06是63.680.28否 上河变500 kV I段母65.265.2016.68是65.190.02否 上河变500 kV II段母65.265.2016.68是65.190.02否 华淮220 kV I段母64.403.1417.02是63.310.30否
[1] ABUR A, GÓMEZ-EXPÓSITO A. Power system state estimation: theory and implementation[M]. New York, USA: Marcel Dekker, 2004.
[2] 于尔铿. 电力系统状态估计[M]. 北京: 水利电力出版社, 1985.
[3] 国家电力调度通信中心. 智能电网调度技术支持系统建设框架[R]. 2009.
[4] Q/GDW 680-2011 智能电网调度技术支持系统系列规范[S]. 北京: 国家电网公司, 2011.
[5] 丁宏恩, 高宗和, 苏大威, 等. 混合量测状态估计相角参考点坏数据问题的处理方法[J]. 电力系统自动化, 2014, 38(9): 132-135.
DING Hongen, GAO Zonghe, SU Dawei, et al. Solution to bad data problem of phase angle reference bus for state estimation with hybrid measurement[J]. Automation of Electric Power Systems, 2014, 38(9): 132-135.
[6] 冯飞, 宋凯, 逯仁贵, 等. 磷酸铁锂电池组均衡控制策略及荷电状态估计算法[J]. 电工技术学报, 2015, 30(1): 22-29.
FENG Fei, SONG Kai, LU Rengui, et al. Equalization control strategy and SOC estimation for LiFePO4 battery pack[J]. Transactions of China Electrotechnical Society, 2015, 30(1): 22-29.
[7] PHADKE A G. Synchronized phasor measurements in power systems[J]. IEEE Computer Applications in Power, 1993, 6(2): 10-15.
[8] BURNETT R O, BUTTS M M, CEASE T W, et al. Synchronized phasor measurements of a power system event[J]. IEEE Transactions on Power Systems, 1994, 9(3): 1643-1650.
[9] 李强, 周京阳, 于尔铿, 等. 基于混合量测的电力系统状态估计混合算法[J]. 电力系统自动化, 2005, 29(10): 30-35.
LI Qiang, ZHOU Jingyang, YU Erkeng, et al. A hybrid algorithm for power system state estimation based on PMU measurement and SCADA measurement[J]. Automation of Electric Power Systems, 2005, 29(10): 30-35.
[10] 赵红嘎, 薛禹胜, 汪德星, 等. 计及PMU量测支路电流相量的状态估计模型[J]. 电力系统自动化, 2004, 28(17): 37-40.
ZHAO Hongga, XUE Yusheng, WANG Dexing, et al. State estimation model with PMU current phasor measurements[J]. Automation of Electric Power Systems, 2004, 28(17): 37-40.
[11] 程云峰, 张欣然, 陆超. 广域测量技术在电力系统中的应用研究进展[J]. 电力系统保护与控制, 2014, 42(42): 145-153.
CHENG Yunfeng, ZHANG Xinran, LU Chao. Research progress of the application of wide area measurement technology in power system[J]. Power System Protection and Control, 2014, 42(42): 145-153.
[12] ZIVANOVIC R, CAIRNS C. Implementation of PMU technology in state estimation: an overview[C] // 4th African Conference in Africa, September 24-27, 1996, Stellenbosch, South Africa: 1006-1011.
[13] CHEN J, ABUR A. Placement of PMUs to enable bad data detection in state estimation[J]. IEEE Transactions on Power Systems, 2006, 21(4): 1608-1615.
[14] 李虹, 赵书强. 基于WAMS/SCADA混合量测的电力系统强跟踪滤波动态状态估计[J]. 电力自动化设备, 2012, 32(19): 101-105.
LI Hong, ZHAO Shuqiang. Power system dynamic state estimation of strong tracking filter based on hybrid WAMS/SCADA measurements[J]. Electric Power Automation Equipment, 2012, 32(19): 101-105.
[15] 卢志刚, 赵号, 刘雪迎, 等. 基于可靠度与可观度的量测优化配置研究[J]. 电工技术学报, 2014, 29(12): 180-187.
LU Zhigang, ZHAO Hao, LIU Xueying, et al. Optimal measurement configuration based on degree of reliability and observability[J]. Transactions of China Electrotechnical Society, 2014, 29(12): 180-187.
[16] 李静, 罗雅迪, 赵昆, 等. 考虑大规模风电接入的快速抗差状态估计研究[J]. 电力系统保护与控制, 2014, 42(22): 113-118.
LI Jing, LUO Yadi, ZHAO Kun, et al. Research of fast and robust state estimation considering large-scale wind power integration[J]. Power System Protection and Control, 2014, 42(22): 113-118.
[17] 赵俊博, 张葛祥, 黄彦全. 含新能源电力系统状态估计研究现状和展望[J]. 电力自动化设备, 2014, 34(5): 7-20.
ZHAO Junbo, ZHANG Gexiang, HUANG Yanquan. Status and prospect of state estimation for power system containing renewable energy[J]. Electric Power Automation Equipment, 2014, 34(5): 7-20.
[18] 荀挺, 张珂珩, 薛浩然,等. 电网调控数据综合智能分析决策架构设计[J]. 电力系统保护与控制, 2015, 43(11): 121-127.
XUN Ting, ZHANG Keheng, XUE Haoran, et al. Framework design of the analysis decision system about the power grid data[J]. Power System Protection and Control, 2015, 43(11): 121-127.
(编辑 魏小丽)
Hybrid measurement based secondary linear state estimation method and its engineering application
DING Hongen1, DAI Zemei2, HUO Xuesong3, ZHOU Jieying4, XU Xiuzhi1, LÜYang1, YU Yu1
(1. State Grid Suzhou Power Supply Company, Suzhou 215004, China; 2. NARI Group Corporation (State Grid Electric Power Research Institute), Nanjing 211106, China; 3. State Grid Jiangsu Electric Power Company, Nanjing 210024, China; 4. State Electric Power Dispatching Center of China, Beijing 100031, China)
In the state estimation based on hybrid measurement of the phasor measuring unit (PMU) and supervisory control and data acquisition (SCADA), once calculations are based on the traditional nonlinear model, it will face some problems such as difficult to determine PMU measurement calculated weight, inaccurately processing of PMU measurement bad data, the change of phase angle reference point and mature commercial program, etc. In order to solve the above problems, this paper proposes a new secondary linear state estimation method with hybrid measurement. This method uses the voltage amplitude of each node and phase angle estimation of the result based on the convergence of traditional nonlinear state estimation and the PMU measurement to re-calculate the secondary linear state estimation. The effectiveness of the method proposed is illustrated using actual example.
state estimation; phasor measurement unit (PMU) measurement; bad data process; weight calculation; reference point
10.7667/PSPC151409
江苏省电力公司科技项目
2015-08-11;
2015-11-03
丁宏恩(1982-),男,通信作者,硕士,高级工程师, 主要研究方向为电网调度自动化与智能化相关技术;E-mail: hongending@163.com 戴则梅(1973-),女,研究员级高级工程师,主要研究方向为电网调度自动化;霍雪松(1977-),男,高级工程师,主要研究方向为电力系统调度运行控制与管理。

