GPU平台二维快速傅里叶变换算法实现及应用
张 全,鲍 华,饶长辉,彭真明( 1. 中国科学院自适应光学重点实验室,成都 61009;. 电子科技大学 光电信息学院,成都 610054; 3. 中国科学院光电技术研究所,成都 61009;4. 中国科学院大学,北京 100049 )
GPU平台二维快速傅里叶变换算法实现及应用
张 全1,2,3,4,鲍 华1,3,饶长辉1,3,彭真明2
( 1. 中国科学院自适应光学重点实验室,成都 610209;2. 电子科技大学 光电信息学院,成都 610054; 3. 中国科学院光电技术研究所,成都 610209;4. 中国科学院大学,北京 100049 )
摘要:NVIDIA在其GPU平台上开发的FFT库CUFFT经过几次升级,但在二维FFT实现上效率还有提升空间,而且对于特定不能与上下文的计算融合,导致多次对Global memory的访问。本文分析合并内存访问事务大小与占用率之间的关系,优化使用GPU存储器资源,对小数据量2次幂二维复数FFT在GPU上的实现进行改进,加速比最高达到CUFFT 6.5的1.27倍。利用实数FFT结果的共轭对称性,算法的效率比复数FFT算法运算量降低了40%。最后将FFT的改进应用到光学传递函数(OTF)的计算中,采用Kernel 融合的方法,使得OTF的计算效率比CUFFT计算方法提高了1.5倍。
关键词:快速傅里叶变换;CUDA;光学传递函数;图形处理器
0 引 言
快速傅里叶变换(Fast Fourier Transform, FFT)是离散傅里叶变换的快速算法。1963年,J.W.Cooley和J.W.Tukey提出的Cooley-Tukey算法是FFT算法的早期版本,该算法以分治法为策略使DFT的运算量从减小到了,计算效率提高1~2个数量级。目前除了Cooley-Tukey算法以外,还涌现出许多高效的算法。其中包括素因子算法(Prime Factor)、分裂基算法,混合基算法等[1]。
在FFT实现方面,MIT开发了基于CPU的FFT算法库FFTW(Fast Fourier Transform in the West,FFTW),该库函数具有很强的移植性和自适应性,能够自动配合所运行的硬件平台,通过最优化搜索,找到最优的组合使运行效率达到最佳。2003年Kenneth Moreland与Edward Angel利用GPU的着色器编译程序把FFT算法移植到了GPU平台上[2]。2007年NVIDIA公司推出CUDA并行开发环境,同时也发布了基于CUDA 的FFT库函数CUFFT,该库进行FFT处理的速度大约是同期CPU进行FFT运行速度的20倍[3]。2008年,Vasily Volkov在GPU上对FFT算法进行改进使一维FFT算法效率比CUFFT 1.1提高3倍[4]。N.K. Govindaraju,B. Lloyd,Y. Dotsenko等人在Volkov的基础上使得一维FFT效率比CUFFT 1.1提高4倍,并实现了二维FFT[5-6]。随后,NVIDIA把Volkov等人改进的算法加入到下一版本的CUFFT中。
本文针对GPU多核处理器架构,通过分析FFT的Cooley-Tukey算法框架,针对小数据量2的幂次方二维FFT在GPU上的实现进行分析,对列做一维FFT变换时,存在非合并内存访问的问题,使得访存效率下降。通过分析调整Block的大小,使得同时读入多列数据进行计算,尽量满足128 Byte的Cache line,将非合并内存访问的影响降到最低。最后将该算法应用到图像处理中常用的光学传递函数(OTF)的计算中,通过Kernel融合的方法提高了OTF的计算效率。
1 算法理论
1.1 Cooley-Tukey DFT算法框架[7]
离散傅里叶变换DFT(Discrete Fourier Transform)将时域信号转换成频域信号。一维DFT计算式:
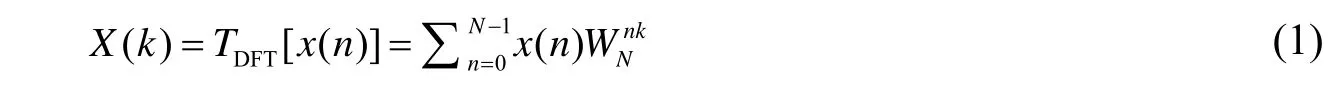


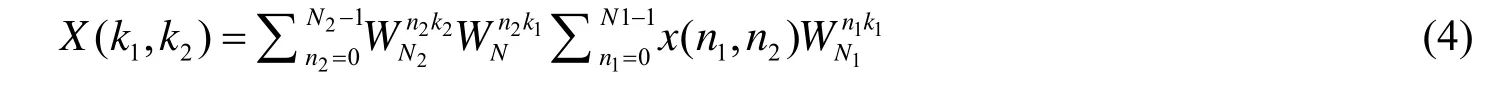
Cooley-Tukey算法主要包括两次索引变换和两次一维小点数DFT,其计算分为如下5步。
Step1: 输入序列根据式(2)做输入索引变换;
Step2: 计算N2个长度为N1点的一维DFT运算(第一级变换);
Step4:计算N1个长度为N2点的一维DFT运算(第二级变换); Step5: 对第二级变换结果按照式(3)做输出索引变换。
1.2 实数FFT算法
设x(n)是2N点的实序列,现将x(n)分为偶数组x1(n)和奇数组x2(n),即:

然后将x1(n)及x2(n)组成一个复序列y(n)=x1(n)+jx2(n),通过N点FFT运算可得到Y(k)=X1(k)+jX2(k),根据前面的讨论,得:
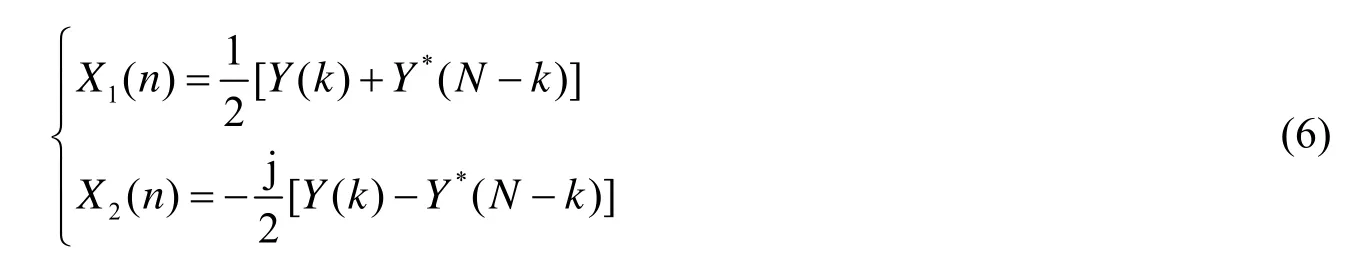
其中:k=0,1,2,..., N -1。为求2N点x(n)所对应的X(k),需求出X(k)与X1(k),X2(k)的关系,即:
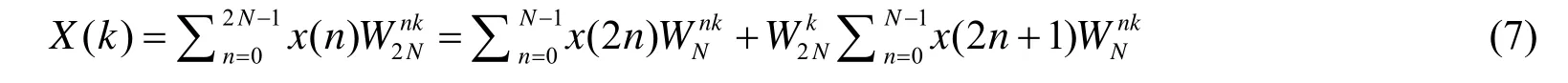
而:
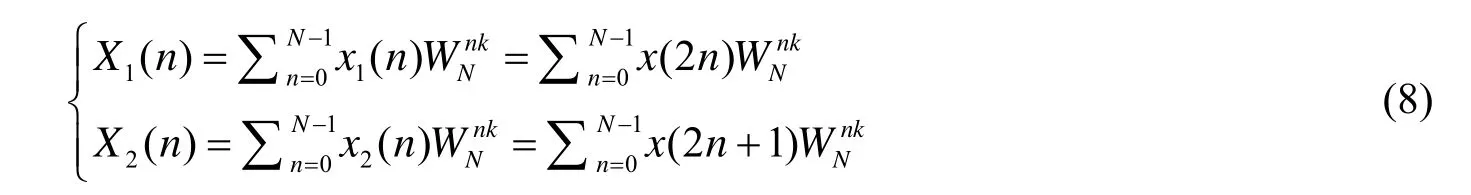
1.3 二维傅里叶变换
二维离散傅里叶变换的定义为
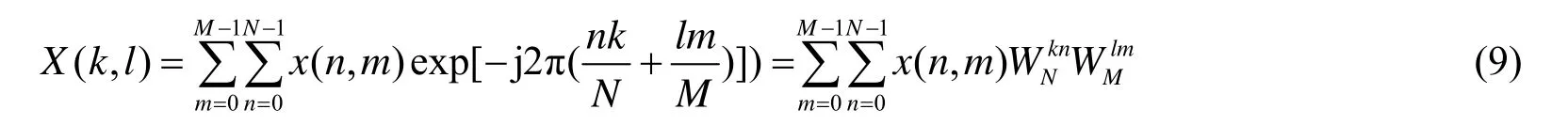
由一维DFT性质知,当x(n)为实序列时,满足复共轭对称性,所以行向量做一维FFT结果只保存M/2+1列数据,如图2(b)所示。然后对M/2+1列作N点DFT得到图2(c)结果。
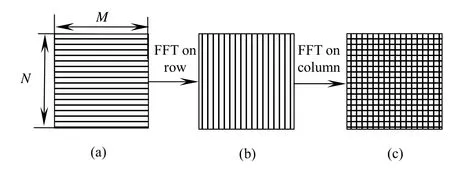
图1 二维复数傅里叶变换计算过程Fig.1 Calculating procedure of 2-D FFT on complex number
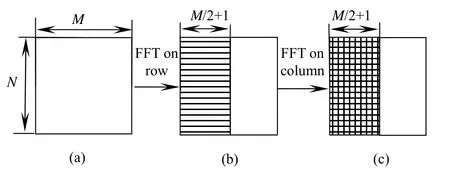
图2 二维实数傅里叶变换计算过程Fig.2 Calculating procedure of 2-D FFT on real number
1.4 GPU编程环境
在CUDA编程模型中,必须要有足够多的活动线程来隐藏访存延时,提高计算性能。可以利用占用率衡量活动线程数。但是程序优化的过程中,高占用率不代表高效率[8]。高占用率虽然提高了并行度,需要在占用率与资源使用之间做出一种折中。
此外,在GPU上进行程序优化主要遵循三个准则,其优先级由高到底。首先是Kernel函数内部应尽量减少全局存储器的访问操作,同时全局存储器访问一定要满足合并访问;其次是设计应尽量使用共享内存(Share Memory, SM)进行Block内部通信,同时对于共享存储器的访问读写也要防止共享存储器的Bank冲突;最后算法设计Block内部应尽可能保持高密集度的寄存器计算,但同时也要协调好如何在片内寄存器资源有限的情况下选择最佳的Thread数量[9]。
2 基于GPU平台的FFT工程实现
根据第一节中Cooley-Tukey算法思想,对于2m点数的FFT可以由基-2、基-4、基-8、基-16等多种组合实现,基数越高,数据重排的次数就越少,同时寄存器需求量也越大,在寄存器资源有限的情况下,高基数导致并行thread数受影响,降低了占用率。综合上述因素,对于2m可以按顺序优先分解为基-16、基-8、基-4、基-2的组合。
对于一维复数FFT,根据向量的大小,一维复数FFT的实现分为三种情况:当向量长度为8或者16时,不需要进行线程之间的数据交换,其计算可以在寄存器中完成;当向量的长度为64、256、512、1 024、2 048和4 096时,线程之间数据交换需要在Share Memoy中完成;当向量的长度超过8 192时,必须通过两次Kernel调用, 数据交换在Global Memory中完成。本文主要针对二维FFT计算进行分析,整个算法执行流程如图3所示,算法分为行方向一维傅里叶变换和列方向一维傅里叶变换。一维傅里叶变换又分为多级,相邻的级间需要同步并且通过Share Memory交换数据。

图3 二维傅里叶变换GPU实现过程Fig.3 Implementation of 2-D FFT on GPU
2.1 行方向一维FFT变换
对于小数据量的二维FFT算法,二维矩阵每一行数据可以放入Share Memory,不需要通过Global Memory进行数据交换。假设数据长度为N的一维向量,将其排列成N1×N2的二维矩阵。计算过程中首先选择合适的N2,使其能够在Share Memory中完成FFT计算。然后确定N1=N/N2,如果N1不能够在Share Memory中完成计算,则对N1进一步分解为N1=N11×N12,以此类推。另外一种解释就是相当于把长度为N的向量,重新排列为多维矩阵,每一维的长度为FFT的一个固定基,其FFT计算称作整个N点FFT的一级。对N的每一次分解都要做一次矩阵转置。以N=512为例,首先,512可以分解为64×8,先做64行8点一维FFT;其次,在Share Memory中进行数据转置,然后,再做8行64点一维FFT,考虑到64点做FFT比较大,将其进一步分解为8×8。通常N存在多种分解例如512还可以分解为2×16×16,或者4×8×16,不同的分解效率也会有差别,基越小运算量越大,尽量避免基-2或者基-4的分解。分解的级越多同步操作越多,所以尽量在满足共享存储要求的前提下采用大基。依据以上原则,N=128的最优分解为16×8而非4×4×8;N=256的最优分解为16×16,而非8×8×4。
512点FFT存储器访问如图4所示,完成一行512点一维FFT需要的线程数为64。为了满足合并内存访问条件,512个数据被分为8组,每组64个数据。每个线程从8组数中各取1个数据存入8个寄存器中。为提高GPU的占用率,Block的大小取64的倍数,使一个Block同时完成多行512点数据的一维FFT。
2.2 列方向一维FFT变换
从GPU硬件的角度来看,GPU上的内存延迟被不同线程束间的切换所隐藏。如果同一线程束的线程访问相邻内存位置,并且内存区域的开始位置是对齐的,这些访问请求会自动组合或者合并。计算能量1.x设备上,合并内存事务最小为128 Byte。如果被合并线程访问的数据比较小,会导致内存带宽迅速下降。费米架构的设备支持32 Byte和128 Byte的合并内存事务。开普勒架构的设备支持32 Byte、64 Byte和128 Byte的合并内存事务。
列方向一维FFT变换与行方向一维FFT变换计算过程一样。区别在于对全局内存的访问方式不一样,在行方向一维FFT变换中线程访问Global Memory是满足合并内存访问的,而列方向一维FFT变换则不是。为了提高访存效率,需要对存储器访问方式进行调整。以double数据类型512×512二维矩阵列FFT变换为例,矩阵中每个数据占16 Byte。本文实验采用的设备为计算能力为3.5的开普勒计算卡,其支持32 Byte、64 Byte、128 Byte三种缓存行模式,为了满足这三种内存合并模式,每个Block分别至少处理2列、4列、8列一维FFT计算,经过实验测试每个Block处理4列一维FFT时效率最佳。512×512 double类型二维矩阵按列FFT变换存储器访问如图5所示,线程数为64×4的二维矩阵,每一列线程访问Global memory中对应的一列数据,每个线程访问列方向间隔为64的8个数据。
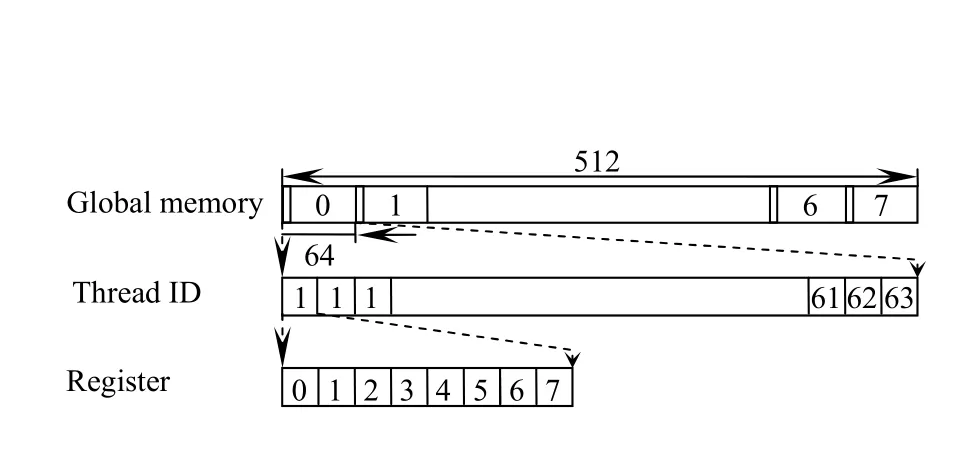
图4 512×512行方向一维FFT变换全局存储器访问Fig.4 Global memory access of 1-D FFT on row for array size of 512×512
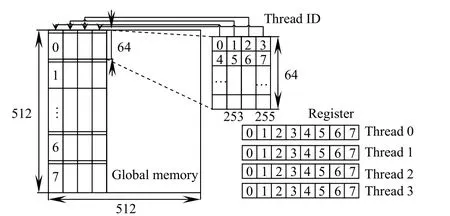
图5 512×512列方向一维FFT变换全局存储器访问Fig.5 Global memory access of batched 1-D FFT on column for array size of 512×512
2.3 FFT在OTF计算中应用[10]
光学成像系统在像面的复振幅可表示为

式中:F-1{}表示傅里叶逆变换,(u, v)和(x, y)分别为瞳面和像面坐标;P(u, v)为广义光瞳函数,可以表示为

式中:j为虚数单位,φ(u, v)为波前相位,p(u, v)为孔径函数。对应成像系统的点扩散函数可表示为
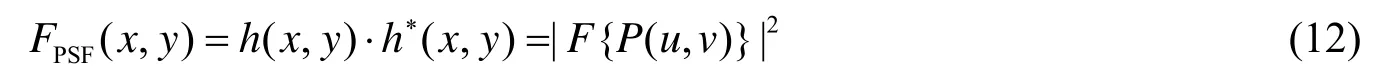
而光学传递函数定义为点扩散函数的傅里叶变换,即

由上所述,OTF的计算分为6步:1) 广义光瞳函数计算;2) 对光瞳函数列方向批量一维IFFT;3) 行方向批量一维IFFT;4) 对取模平方运行得到点扩散函数;5) 对点扩散函数列方向批量一维FFT;6) 行方向批量一维FFT。在GPU上实现时,由于1)和2)计算过程中每个数据相互独立,可以合并,由一个Kernel完成计算;二维FFT计算中,交换行方向一维FFT和列方向一维FFT的计算次序不影响计算结果,交换5)和6)的次序,从而3) ~5)行与行之间数据相互独立,三步可以合并由一个Kernel 完成。整个合并过程使得Kernel数由6个减小为3个。
3 实验结果分析
3.1 实验环境
本文实验所采用的硬件配置:Intel(R) core(TM) i7-3930k主频3.2 GHz CPU,内存8 G,NVIDIA Telsa K20c GPU。软件配置:Windows 7 64-bit操作系统,VS2010+CUDA6.5编程环境。
3.2 FFT并行设计性能比较
二维FFT的GPU实现分两步执行,首先进行行方向批量一维FFT,然后再列方向批量一维FFT,行方向计算时Global memory满足合并内存访问,而列方向时不利于合并内存访问,根据不同的数据类型,尽量满足相邻线程访问事务大小的数据。对列方向一维FFT时,一次读入多列可以增加合并内存数据块,但是会消耗过多的共享内存和寄存器资源从而降低了占用率,所以需要在内存访问效率与GPU占用率之间做出折中的选择,针对不同的配置其占用率和内存访问效率都不一样,表1分别针对Float2(Float型复数) 和Double2(Double型复数)数据类型的列方向FFT在不同线程配置下做了测试。本实验采用的Telsa K20c GPU,支持32 Byte、64 Byte、128 Byte的合并内存事务。从实验数据我们知道占用率不代表高性能,也不是内存合并事务越大性能越高,需要在这两者之间进行折中。对于256×256、512×512的二维FFT,64 Byte的合并内存事务使得占用率不会最低,同时内存访问效率也不是最低,是一种较优的配置。
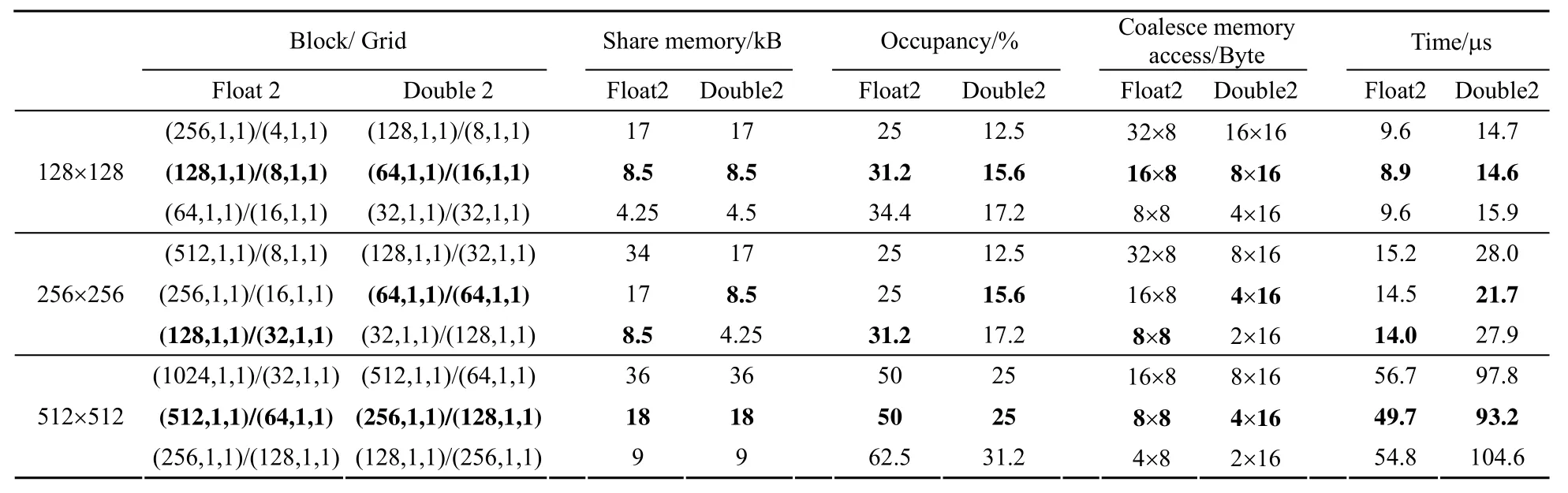
表1 Float 2型和Double 2型数据Kernel 2不同线程配置性能比较Table 1 Performance comparison of Kernel2 for Float2 and Double2 under different thread configuration
对CPU平台下FFTW库函数,以及GPU平台下CUFFT和本文方法,分别做1 000次二维FFT计算其平均值,三种方法都不考虑数据拷贝时间和内存分配时间,另外FFTW和CUFFT库函数时间只包括执行时间,不包括配置时间。表2分别为数据大小为128×128、256×256、512×512的二维FFT执行时间。从表中可以看出,数据较小时,CUFFT与FFTW的加速比较小;数据量变大时,加速比随之增加,其范围在2.5~53.7之间。对于128×128大小的二维FFT GPU资源并没有充分利用,但是较之FFTW还是具有一定优势。本文的方法相对于CUFFT也有提高,双精度512×512大小二维复数FFT计算效率是CUFFT的1.24倍。利用实数FFT计算结果的共轭对称性,512×512的二维双精度实数FFT计算效率是CUFFT的1.36倍。

表2 128×128、256×256、512×512二维FFT性能比较Table 2 Performance comparison of 2-D FFT for array of 128×128, 256×256, 512×512 μs
针对前面提到的OTF的计算,采用CUFFT库函数方法和本文FFT分别对其实现,其性能如图6所示,由于本文方法采用Kernel合并提高了GPU指令并行度,降低了Global Memory的访问,对于512×512的双精度二维OTF计算效率是采用CUFFT方法的1.51倍。
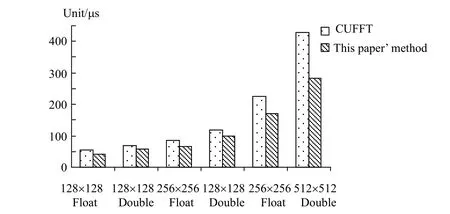
图6 使用库函数与本文方法计算OTF执行时间比较Fig.6 Comparison of execution time between library method and this paper’ method
4 结论及展望
本文分析了Cooley-Tukey FFT计算框架,完成了基于CUDA编程模型的小数据量2的幂次方二维FFT 在GPU上的实现,在合并内存访问与GPU占用率之间进行折中处理,实验结果表明,该方法效率是CUFFT 的1.24倍。OTF的GPU实现利用二维FFT计算特性,交换了一维行变换和列变换的次序,通过Kernel合并的方法,使OTF的计算效率相比CUFFT方法提高1.5倍。下一步工作主要针对大数据量的二维FFT并行化和非基-2 FFT的实现。
参考文献:
[1] Rao K R,Kim D N,Hwang J J. 快速傅里叶变换:算法与应用 [M]. 北京:机械工业出版社,2012:1-33.
[2] Moreland K,Angel E. The FFT on a GPU [C]// Proceedings of the ACM Siggraph/Eurographics Conference on Graphics Hardware,San Diego,California,July 26-27,2003:112-119.
[3] 赵丽丽,张盛兵,张萌,等. 基于的高速计算 [J]. 计算机应用研究,2011,28(4):1556-1559.
ZHAO Lili,ZHANG Shengbing,ZHANG Meng,et al. High performance FFT computation based on CUDA [J]. Application Research of Computers,2011,28(4):1556-1559.
[4] Volkov V,Kazian B. Fitting FFT onto the G80 Architecture [M]. University of California,2008,E63(40):1-12.
[5] Naga K Govindaraju,Brandon Lloyd,Yuri Dotsenko,et al. High performance discrete Fourier transforms on graphics processors [C]// Proceedings of the 2008 ACM/IEEE conference on Supercomputing,Austin,Texas,November 15-21,2008:1-12.
[6] Brandon L D,Boyd C,Govindaraju N. Fast computation of general Fourier Transforms on GPUs [C]// IEEE International Conference on Multimedia and Expo,Hannover,Germany,June 23-26,2008:5-8.
[7] 杨丽娟,张白桦,叶旭桢. 快速傅里叶变换FFT及其应用 [J]. 光电工程,2004,31(增):1-3.
YANG Lijuan,ZHANG Baihua,YE Xuzhen. Fast Fourier transform and its applications [J]. Opto-Electronic Engineering,2004,31(Suppl):1-3.
[8] Volkov V. Better performance at lower occupancy [C]// Proceedings of the GPU Technology Conference,San Jose,California,September 20-23,2010.
[9] Rob Farber. 高性能CUDA 应用设计与开发:方法与最佳实践 [M]. 北京:机械工业出版社,2013:1-27.
[10] Jim Schwiegerling. Relating wavefront error apodization,and the optical transfer function on-axis case [J]. Journal of the Optical Society of America A(S1520-8532),2014,31(11):2476-2483.
Realization and Application of Two-dimensional Fast Fourier Transform Algorithm Based on GPU
ZHANG Quan1, 2, 3,4,BAO Hua1,3,RAO Changhui1,3,PENG Zhenming2
( 1. Key Laboratory on Adaptive Optics, Chinese Academy of Sciences, Chengdu 610209, China; 2. School of Optoelectronic Information, University of Electronic Science and Technology of China, Chengdu 610054, China; 3. Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu 610209, China; 4. University of Chinese Academy of Sciences, Beijing 100049, China )
Abstract:NVIDIA as the inventor of the GPU provides a library function CUFFT for computing Fast Fourier Transform (FFT). After several generations update of CUFFT, there is still promotion space and it is not suit for kernel fusing on GPU to reduce the memory access and increase the Instruction Level Parallelism (ILP). We develop our own custom GPU FFT implementation based on the well-known Cooley-Tukey algorithm. We analyze the relationship of coalesce memory access and occupancy of GPU and get the optimal configuration of thread block. The results show that the proposed method improved the computational efficiency by 1.27 times than CUFFT 6.5 for double complex data 512×512. And then it is used to the computation of OTF with kernel fusing strategy, and it improved the efficiency of computation about 1.5 times than conventional method using CUFFT.
Key words:FFT; CUDA; optical transfer function (OTF); graphic processing unit (GPU)
作者简介:张全(1985-),男(汉族),甘肃武威人。博士研究生,主要研究工作是GPU高性能计算,图像处理。E-mail: quanzhang100@126.com。
基金项目:国家自然科学基金(11178004);中国科学院实验室创新基金(YJ14K018)
收稿日期:2015-02-04; 收到修改稿日期:2015-06-12
文章编号:1003-501X(2016)02-0069-07
中图分类号:TP391
文献标志码:A
doi:10.3969/j.issn.1003-501X.2016.02.012

