基于多帧序列运动估计的实时立体视觉定位
许允喜,陈 方( 湖州师范学院 信息工程学院,浙江 湖州 313000 )
基于多帧序列运动估计的实时立体视觉定位
许允喜,陈 方
( 湖州师范学院 信息工程学院,浙江 湖州 313000 )
摘要:同时优化运动和结构的集束调整方法存在对初始值依赖太大,收敛速度慢,收敛发散等数值稳定性低的缺点。本文提出了一种新的用于立体视觉定位的多帧序列运动估计方法,该方法收敛速度快,能收敛到全局最小,可大大减少积累误差。立体视觉定位仿真实验和户外智能车真实实验表明:基于多帧运动估计的实时立体视觉定位算法在计算精度、运行时间、抗噪声、对初始参数的稳定性方面都优于基于集束调整的实时立体视觉定位算法。关键词:实时视觉定位;视觉导航;集束调整;多帧序列运动估计
0 引 言
基于视觉的自主导航移动机器人需要实时地获取自己的位置(定位)[1-3]。实时立体视觉定位算法一般利用二帧之间的特征匹配信息进行运动估计(单帧运动估计),对单帧运动估计参数进行级联计算出摄像机全局定位信息,这种方法使小的运动估计误差随图像序列不断积累,从而导致移动机器人在长距离行进下定位精度不高。集束调整(Bundle Adjustment)[4-5]是计算机视觉领域的从运动恢复结构的关键技术,其采用离线方式同时对所有图像帧的摄像机位姿和特征点3D坐标参数进行非线性优化。集束调整优化函数的雅克比矩阵是稀疏结构,利用该稀疏结构可大大提高计算速度,所以目前使用的集束调整都指稀疏集束调整。
由于实时需求,对所有帧进行参数优化调整是不可行的,所以有研究者提出了局部稀疏集束调整方法并用于实时立体视觉定位[6-8],其采用时间滑动窗的形式,每行进一帧则对最后几帧图像进行优化调整。局部稀疏集束调整通过同时优化运动和结构来建立多帧之间的特征点匹配信息,即同一个3D点投影在不断运动的摄像机图像上,利用投影误差最小来同时优化运动和结构,把许多帧特征点之间的匹配信息联系在一起,作为最后一步优化步骤可大大提高立体视觉定位的精度[6-8]。但该方法对初始值依赖太大,特别是远距离特征点或长的运动序列会造成收敛速度慢或收敛发散等数值稳定性低的缺点。针对集束调整的缺点,本文提出了一种新的用于实时立体视觉定位的多帧序列运动估计方法。与集束调整不同的是:摄像机位姿参数不采用公共世界坐标表达,而采用相邻摄像机相对位姿表达,非相邻摄像机帧之间的相对位姿由相邻摄像机帧的相对位姿级联表达,只优化运动不优化结构,多帧序列中非相邻帧之间的运动约束直接用相邻帧运动级联表达,这大大减少LM参数优化的数值不稳定性问题。本文提出的算法具有收敛速度快,能收敛到全局最小的优点,在长距离行进中,多帧序列运动估计鲁棒性高,能够得到更高的定位精度。
立体视觉定位仿真实验和户外智能车真实实验表明:基于多帧序列运动估计的实时立体视觉定位算法在计算精度、运行时间、抗噪声、对初始参数的稳定性方面都优于基于集束调整的实时立体视觉定位算法。
1 多帧序列运动估计算法
1.1 多帧图像序列运动约束
在特征点匹配跟踪时,有许多特征点会同时被两帧以上的立体相机观测到,产生特征点多帧匹配约束。由于特征点非相邻帧之间也存在特征匹配约束,从而产生了多帧图像序列运动约束,除了连续相邻二帧之间存在运动约束,非相邻帧之间也存在运动约束。传统的单帧运动估计算法只利用了连续相邻二帧之间的匹配信息。很显然,把相邻帧和非相邻帧的投影几何约束统一到运动优化算法中形成多帧运动参数优化将有助于提高图像序列运动估计的精确性和鲁棒性。
1.2 集束调整方法
在集束调整方法中,首先把所有匹配的特征点都表达为相对于全局坐标系的世界点,摄像机位姿参数也表达为相对于全局坐标系。把这些世界特征点重投影在每个摄像机上,建立图像重投影误差函数,利用Levenberg-Marquard(LM)优化方法同时优化特征点3D世界坐标和摄像机位姿参数。多帧匹配运动约束都包含在图像重投影误差函数中以及特征点世界坐标和摄像机位姿参数优化进程中。如果仅优化运动(摄像机位姿参数),不优化结构(特征点3D世界坐标),则集束调整相当于单帧运动估计。
1.3 多帧运动估计算法
摄像机运动后前后两帧中对应匹配点的3D坐标分别为P =(X,Y, Z )T和P′=(X′,Y′, Z′)T,假定R和t分别为旋转和平移的变换参数,则有:

若特征点i在运动后左右相机上测量的2D投影坐标为mli=(ulivli)、mri=(urivri),则给定运动参数后特征点在左右相机上的2D再投影和实际测量位置之间的误差平方和为
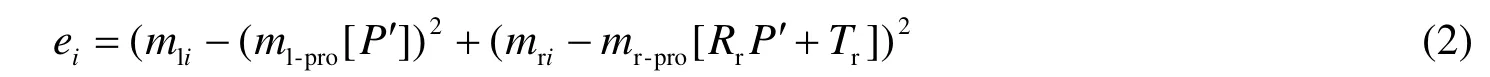
其中:Rr,Tr分别为立体相机中右相机相对于左相机的相对旋转和平移,为已知固定值。设立体相机的实际测量图像位置为:mi=(mlimr i),由式(1)可知,相邻帧运动参数θ(R和t)包含在P′中,设立体相机的图像再投影函数向量为:f(θ)=(ml-pro[P']mr-pro[RrP′+Tr])。则可得到下式:

设摄像机帧j与经过若干次运动后的摄像机帧k存在特征点匹配,则由式(1)可得:
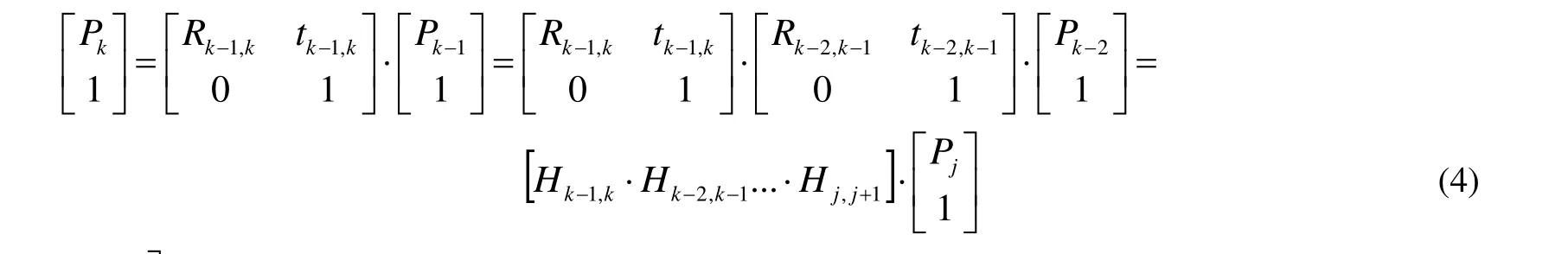
Hj,j+1=为4×4的齐次坐标矩阵,表示时间j相邻帧之间的运动参数。则摄像机帧j与帧k之间的相对位姿参数随时间帧的级联表达为Hj,j+1Hj+1,j +2...Hk -1,k,则摄像机帧k相对于帧j的位姿参数为由式(4)和式(5)可知,任意非相邻帧之间的特征点匹配投影关系可由相邻帧位姿参数表达。

设特征点i被摄像机帧j和帧k同时观测到,则fk,j,i(θ)表示特征点i在摄像机运动后的再投影图像坐标。则再投影图像误差函数可以表示为

其中mk,i表示特征点i在立体摄像机帧k上投影的真实图像测量坐标。
本文提出的多帧序列运动估计方法,把相邻帧、非相邻帧之间的匹配约束统一表达为投影约束方程,运动参数包含在这些方程中,通过优化算法求出使这些方程所有投影误差最小的运动参数。设立体相机共产生N次运动,则运动参数θ={θk,i =1,2,...,N}是6×N维的向量。设共有Q个特征点,则总的透视投影误差函数平方和可表示为
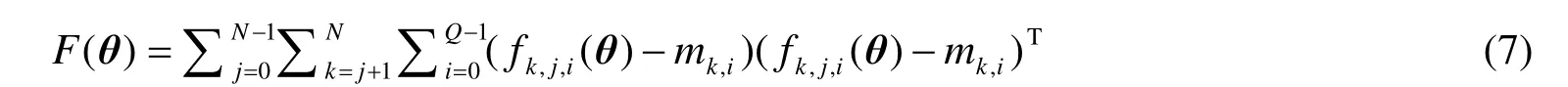

式(8)可以通过LM非线性最小平方迭代算法求解,求出使投影误差平方和最小的运动参数θ。在计算参数更新步长时需求解下列方程:

其中J为f(θ)的雅克比矩阵。
1.4 算法的计算复杂度和数值稳定性对比
在集束调整中,特征点的匹配联系通过把匹配的特征点表达为同一世界坐标来实现,通过投影误差同时优化特征点的3D世界坐标和摄像机位姿参数。对于N帧图像,Q个特征点的视频序列,集束调整的透视投影误差函数为
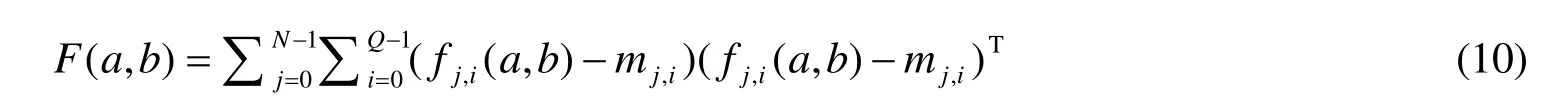
下面分析稀疏集束调整和本文的多帧序列运动估计的计算复杂度。把计算复杂度分为二部分:J矩阵计算以及线性方程求解。集束调整的J为fj,i(a, b)的雅克比矩阵,由A、B矩阵计算得到:。
A矩阵需要计算的微分次数:Q .N2,B矩阵需要计算的微分次数:Q.N .Q。则J矩阵的微分计算复杂度为:Q.N2+Q.N.Q 。利用J矩阵的稀疏结构,JTJ可表达如下:。
U、V、W为Hession矩阵JTJ的子矩阵,由A,B矩阵计算得到,则:

εa和εb由得到,a∂可由下式计算:
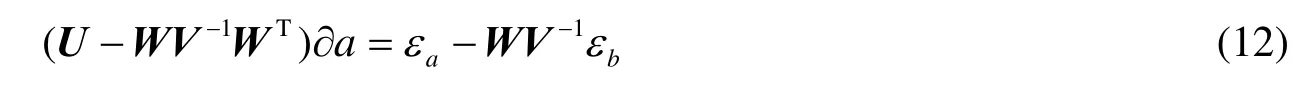
∂b可由下式计算:

式(12)和式(13)的计算复杂度主要为-1V的计算和线性方程(13)的求解。线性方程的求解也为矩阵求逆的过程。矩阵求逆的计算复杂度为矩阵大小的3次方,所以V-1和方程(12)的计算复杂度为O(Q3+N3)。
在本文的多帧序列运动估计中,帧间的运动约束直接用摄像机间相对运动参数表达,通过透视投影误差只优化摄像机运动参数。在方程(9)中,多帧序列运动估计J矩阵的微分计算次数为:QN(N +1) N/2。在参数优化调整中,N的值较小(在满足实时性条件下,N≤4 ),而匹配特征点数很大(Q≥100)。则可以得出:Q.N2+Q.N.Q >QN(N+1)N/2。
而多帧序列运动估计中式(9)线性方程求解的计算复杂度为O(N3),明显小于O(Q3+N3)。综合以上分析,多帧序列运动估计方法的计算复杂度远小于稀疏集束调整的计算复杂度。
在集束调整中,远距离特征点或长的图像序列会造成收敛速度慢、收敛发散等数值不稳定问题[5]。由于采用公共坐标系,摄像机位姿参数和3D特征点都只用一个坐标系表达,这大大增加了LM优化过程中的数值不稳定性[5],特别当计算远距离特征点3D坐标且摄像机位姿参数还不够精确时。在本文的多帧序列运动估计中,摄像机位姿不采用公共坐标系且不优化3D点坐标,多帧序列中非相邻帧之间的运动参数直接由相邻摄像机运动参数级联表达,这大大增加了数值稳定性、收敛速度和对初始值的鲁棒性。集束调整收敛速度慢以及陷入局部最小的机会很大,本文的多帧序列运动估计方法改进了集束调整的优化性能,算法收敛速度快,能收敛到全局最小。所以在长距离行进中,多帧序列运动估计鲁棒性高,能够得到更高的定位精度。
2 实 验
本文建立了数值仿真实验和户外真实智能车实验,对集束调整和多帧序列运动估计这二种方法在实时立体视觉定位上的性能进行了详细的对比。实验中用于对比的集束调整是指用于实时立体视觉定位的局部稀疏集束调整[6-7,9-10]。立体视觉定位的详细计算步骤如下:1) 计算当前帧左图像的CenSurE特征[6,11]和U-SURF描述符[12]。2) 对CenSurE特征采用立体匹配方法进行左右图像立体匹配。3) 利用U-SURF描述符,计算和前一帧的特征匹配集。4) 利用相邻帧之间的特征匹配和基于RANSAC的位姿估计算法计算得到匹配内点和初始运动参数。5) 根据相邻帧之间的匹配内点得到前N帧的特征匹配集,利用本文的多帧序列运动估计算法对初始运动参数进行非线性优化。实验包含仿真实验和室外真实智能车实验。仿真实验在本文算法框架下进行,但由于使用仿真数据,所以略去了特征点检测和匹配步骤。由于立体视觉定位是实时视频在线计算,对实时性要求很高,所以基于精度和实时性二方面考虑,实验中N的值取3。
2.1 仿真实验
首先建立了立体视觉定位仿真实验,实验条件为:立体相机的等效焦距为490,基线长度为0.12 m,图像大小为640 pixels×480 pixels。在立体匹配和前后帧匹配中都加入高斯噪声和30%的误匹配。仿真实验中行进路线为一“正方形”,共有500帧,约150 m。定位结果采用3D位置和姿态角度的均方根误差:表示。为了验证本文算法的实时性能,本文运用VC++. NET开发工具,在主频为3.2 GHz,内存为4G的PC机上对算法进行了在线测试。
由于在立体匹配和特征跟踪中会不可避免的出现错误,所以在序列运动优化前需要排除错误匹配,得到匹配内点和初始位姿(运动)参数。仿真实验和室外真实智能车实验中内点估计和初始位姿估计均采用精度最高的基于RANSAC的3D-2D位姿估计算法[12]。另外,为了更好地对比BA和MME的性能,在序列优化前先采用单帧运动估计方法进行优化,即先采用仅优化运动,不优化结构的集束调整(MBA),从而得到更精确的运动参数初始值。表1给出了实验结果。在二种不同的运动参数初始值下经过MME优化后的定位误差都明显小于BA优化后的定位误差。MME在二种初始值条件下都收敛于同一个值,而BA在3D-2D+MBA方法下比在单独3D-2D方法下能收敛到更精确的值。这说明:BA算法数值稳定性差,对初始值依赖度大,而MME不依赖初始值,能全局收敛。为了表明即使在最精确的初始值条件下,本文算法仍优于BA方法,后面的实验均采用3D-2D+MBA方法。
MME表示本文提出的多帧序列运动估计方法,BA表示集束调整方法。MME运行时间远远低于BA的运行时间,BA的运行时间为37 ms,而MME的优化时间只有13 ms,在计算资源有限或实时性要求较高的视觉计算场合下,MME的计算优势很明显。

表1 不同初始值条件下立体视觉定位结果对比Table 1 Stereo visual localization comparison with different initial value
表2给出了不同噪声水平下立体视觉定位结果(位姿均方根误差和最大误差)对比。从实验结果看,在各种噪声水平下基于MME的视觉定位算法的位姿均方根误差和最大误差都低于基于BA的视觉定位算法,计算精度更高。其中,噪声越大二种定位精度差距越大,表明:基于MME的视觉定位算法对噪声更加鲁棒。图1给出了一组噪声方差为1.0 pixels的运动估计结果对比图,可以看出:基于BA的定位算法较MME偏离基准轨迹更远。
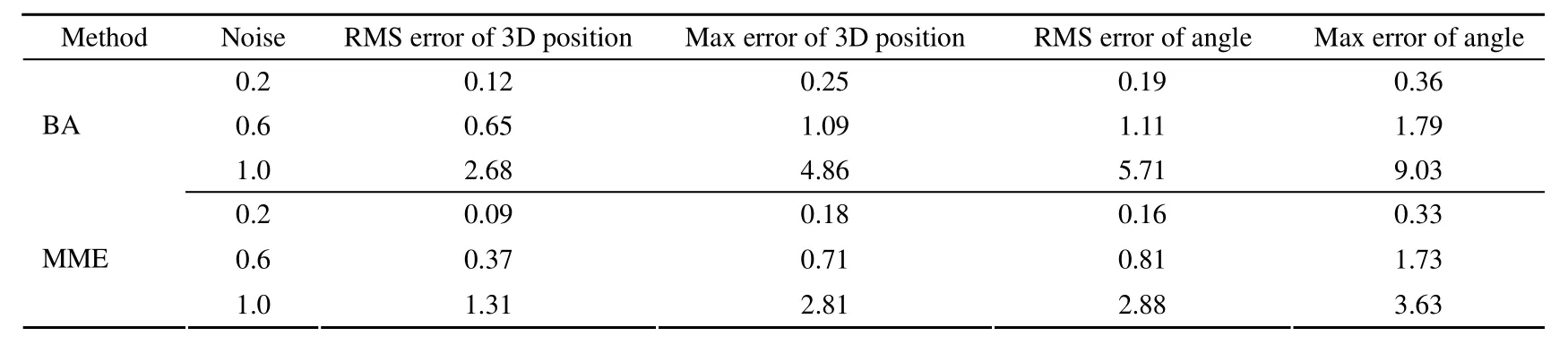
表2 不同噪声水平下立体视觉定位结果对比Table 2 Stereo visual localization comparison with different noise level
2.2 室外真实智能车实验
本文采用“New College Dataset” (感谢牛津大学移动机器人研究小组提供)进行了真实智能车户外立体视觉定位实验。实验采用了数据集中的1个闭环路线(即起点和终点重合),如图2所示,测量定位误差即为闭环3D位置和姿态误差。实验结果如图3和表3。从表3可以看出,本文的基于MME的定位算法精度明显高于基于BA的定位算法精度,均方根闭环位置误差减少了0.55 m,闭环姿态误差减少了1.13°。
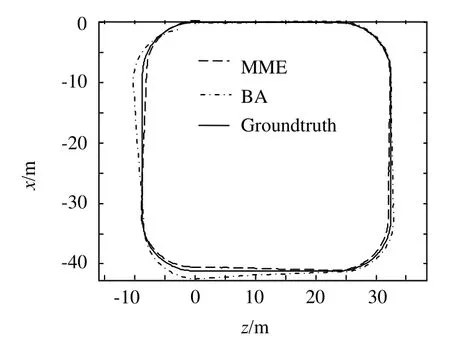
图1 真实运动轨迹及估计运动轨迹Fig.1 Real and estimated motion trajectories

图2 牛津大学数据集的航拍位置Fig.2 Oxford data: aerial view of location
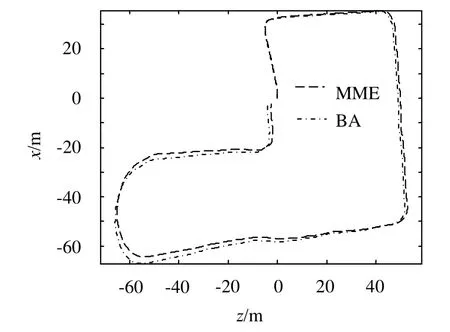
图3 运动估计轨迹对比Fig.3 Estimated motion trajectories comparison

表3 闭环误差对比Table 3 Loop closure error comparison
3 结 论
本文提出了一种新的多帧序列运动估计方法。立体视觉定位实验结果表明,算法具有优化精度高、鲁棒性强、实时性高的优点,优于经典的集束调整方法。算法还有许多进一步深入研究的课题,如多帧序列运动估计的误差传播数学分析以及在实时三维地图重建中应用。
参考文献:
[1] COMPORT A I,MALIS E,RIVES P. Real-time quadrifocal visual odometry [J]. International Journal of Robotics Research (S0278-3649),2010,29(2):245-266.
[2] 彭勃,周文晖,刘济林. 基于Harris角点检测的立体视觉里程计 [J]. 兵工学报,2007,28(12):1498-1502.
PENG Bo,ZHOU Wenhui,LIU Jilin. Harris Corner Dectection-based Stereo Visual odometry [J]. Acta Armamentaii,2007,28(12):1498-1502.
[3] FRAUNDORFER F,SCARAMUZZA D. Visual Odometry:Part II:Matching,Robustness,Optimization,and Applications [J]. IEEE Robotics & Automation Magazine(S1070-9932),2012,19(2):78-90.
[4] Agarwal S,Snavely N,Seitz S M,et al. Bundle adjustment in the large [C]// Proceeding of 11th European Conference on Computer Vision,Crete,Greece,September 5-11,2010:29-42.
[5] Engels C,Stewenius H,Nister D. Bundle adjustment rules [C]// Proceeding of Photogrammetric Computer Vision Conference,Bonn,Germany,September 20-22,2006:266–271.
[6] 吴伟仁,王大轶,邢琰,等. 月球车巡视探测的双目视觉里程算法与实验研究 [J]. 中国科学:信息科学,2011,41(12):1415-1422.
WU Weiren,WANG Dayi,XING Yan,et al. Binocular visual dometry algorithm and experimentation research for the lunar rover [J]. Scientia Sinica Informationis,2011,41(12):1415-1422.
[7] Sunderhauf N,Protzel P. Towards Using Bundle Adjustment for Robust Stereo Odometry in Outdoor Terrain [C]// Proceedings of Towards Autonomous Robotic Systems,Guildford,UK,September 4-6,2006:206-213.
[8] Konolige K,Agrawal M,Sola J. Large-scale visual odometry for rough terrain [C]// Proceedings of 13th International Symposium of Robotics Research,Hiroshima,Japan,November 26 -29,2007:201-212.
[9] Lourakis M I A,Argyros A A. SBA:A Software Package for Generic Sparse Bundle Adjustment [J]. ACM Transactions on Mathematical Software(S0098-3500),2009,36(1):1-30.
[10] Agrawal M,Konolige K. CenSurE:Center surround extremas for realtime feature detection and matching [C]// Proceeding of 10th European Conference on Computer Vision,Marseille,France,October 12-18,2008:102-115.
[11] Bay H,Tuytelaars T,Gool L V. SURF:Speeded up robust features [C]// Proceeding of 10th European Conference on Computer Vision,Graz,Austria,May 7-13,2006:404-417.
[12] Alismail H,Browning B,Dias M B. Evaluating Pose Estimation Method for Stereo Visual Odometry on Robots [C]// Proceedings of the 11th International Conference on Intelligent Autonomous Systems,Ottawa,Canada,August 30-September 1,2010:101-110.
本期组稿:杨淇名
责任编辑:谢小平
英文编辑:庞 洪
Real-time Stereo Visual Localization Based on Multi-frame Sequence Motion Estimation
XU Yunxi,CHEN Fang
( Institute of Information Engineering, Huzhou University, Huzhou 313000, Zhejiang Province, China )
Abstract:Bundle adjustment which simultaneously refines motion and structure has the fault of low numerical stability, such as dependence on the initial value, slow convergence speed, and convergence divergence. In this paper, we propose a new multi-frame sequence motion estimation method for stereo visual localization. The method has the fast convergence speed, can converge to the global minimum, and greatly reduce the accumulated error. Stereo visual localization experiments with simulated data and outdoor intelligent vehicle show that our algorithm outperforms bundle adjustment in terms of run-time, accuracy, resistance to noise and dependence on the initial value.
Key words:real-time visual localization; visual navigation; bundle adjustment; multi-frame sequence motion estimation
作者简介:许允喜(1978-),男(汉族),江苏句容人。讲师,博士研究生,主要研究工作是计算机视觉。E-mail:xuyunxi@hutc.zj.cn。
基金项目:国家自然科学基金项目(61370173);湖州师范学院校级科研项目成果(KX24071)
收稿日期:2015-03-16; 收到修改稿日期:2015-07-01
文章编号:1003-501X(2016)02-0089-006
中图分类号:TP391.41
文献标志码:A
doi:10.3969/j.issn.1003-501X.2016.02.015

