基于异质性分类的小波域SAR图像去斑

侯建华，陈 稳，刘欣达，陈少波( 中南民族大学 智能无线通信湖北省重点实验室，武汉 430074 )



基于异质性分类的小波域SAR图像去斑

侯建华，陈 稳，刘欣达，陈少波
( 中南民族大学 智能无线通信湖北省重点实验室，武汉 430074 )

摘要：提出了一种非同态滤波框架下的小波域SAR图像相干斑抑制算法。将小波域中的后向散射信号和斑点噪声分别建模为正态逆高斯分布、高斯分布，在贝叶斯最大后验准则下推导出信号估计的表达式；为了提高模型参数的估计精度，引入多尺度局部变差系数作为异质性测度，并提出用对数正态分布对该测度进行拟合；基于异质性测度的统计分布特点，本文对小波子带中的系数进行分类，用累积量的估计方法计算每一类小波系数的模型参数。实验结果表明，与传统的同态滤波框架下的同类算法，以及与未采用分类技术的非同态滤波同类算法相比较，本文算法在主、客观性能评价上均有一定的优势，取得了较好的去斑效果。本文提出的基于异质性测度对小波系数分类的思想为SAR图像去斑算法的研究提供了一种新的途径。

关键词：SAR图像去斑；正态逆高斯分布；异质性测度；分类

0 引 言

由于合成孔径雷达(Synthetic Aperture Radar, SAR)图像固有的相干成像特点，在获取SAR图像时不可避免地会引入相干斑，严重地阻碍了后续的图像处理工作，如图像分割、图像分类、目标识别和边缘检测等等。因此，相干斑抑制是SAR图像预处理中一个重要的研究课题。

近二十年来，小波变换因其所具有的诸多良好特性，在SAR图像去斑处理中得到了广泛的应用。由于相干斑噪声的乘性特征，需要首先将其变换为加性噪声的形式，为此有两种方法：1) 直接对含斑图像取对数变换；2) 在形式上将含斑图像分解为信号与噪声相加，但该噪声实际与信号相关。前者称为同态滤波方法，后者称为非同态滤波。同态滤波方法的一个优势在于可以借用成熟的去除加性噪声的理论和技术，因此早期的SAR图像去斑算法大多属于此类方法[1-2]，但由于对数变换的非线性，这类方法会造成同质区域后向散射系数的损失。近年来，非同态滤波算法受到了更多研究者的关注[3-5]。

异质性测量与分析在SAR图像处理领域得到了成功的应用，异质性反映了图像纹理信息变化程度，主要用来描述同一目标区域内不同场景之间的差别[6]。目前异质性测量方法主要包括：基于变差系数[7]、基于算术与几何均值比[8]、基于信息论的方法[9]，这些方法已被应用于小波域SAR图像去斑，且其效果还是比较显著的。例如，文献[10]提出了多尺度局部变差系数的概念；文献[5]提出了以“纹理”能量作为异质性测度，对小波系数进行分类的思想。与[5]类似，文献[11]也以异质性测度为依据对小波系数进行分类，并根据异质性对阈值做自适应调整。此外，文献[6]在空间域从信息论的角度出发，提出了一种新的定量化测量SAR图像异质性参数的指标，并用于斑点噪声抑制。

本文提出了一种将小波域贝叶斯去噪与异质性测量相结合的SAR图像去斑算法。采用非同态滤波框架，对小波域后向散射信号和斑点噪声的统计分布建模，求出Bayesian MAP估计表达式；将文献[10]提出的多尺度局部变差系数作为异质性测度对小波系数分类，分别计算不同类别小波系数所对应的模型参数，从而提高模型参数的估计精度，最终改善去斑算法的性能。

1 小波域贝叶斯SAR图像去斑

1.1 Bayesian 最大后验概率估计

假设斑点噪声完全发育，则SAR图像可以表示为以下乘性噪声模型：

式中：Y为噪声污染的观测信号，即含斑图像；X为待估计的真实无噪信号，Z为与X相互独立的相干斑噪声，对上式做平稳小波变换(SWT)：

式中：wY、wX及wN分别对应Y、X和N=X( Z -1)的小波系数。根据最大后验概率估计(MAP)准则，在给定观测数据wY条件下，使得后验概率最大的wX即为真实信号的估计：

与自然图像类似，真实的SAR图像一般是由大部分的平滑区域加小部分的异质区域(边缘和纹理)构成，平滑区域小波系数趋近于零，而异质区域小波系数幅值偏大，从直方图分布上看，各细节子带中的小波系数表现出高峰度、尖峰型和重拖尾的非高斯性，因此高斯分布已经不能很好的描述这种分布特性。正态逆高斯分布(Normal Inverse Gaussian, NIG)是由具有不同均值的高斯分布和反高斯分布构成的混合模型，在理论上，其参数选取的灵活性有助于克服传统先验模型的缺陷[12]。近年来，已经有文献报道将NIG应用于乘性斑点噪声的处理[4，13]。NIG概率分布密度函数(pdf)为

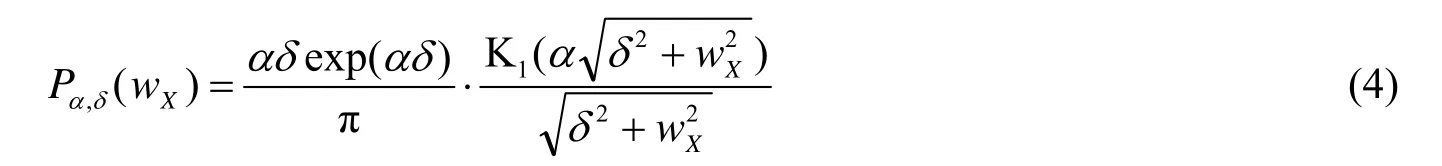
其中：K1为第二类一阶修正贝塞尔函数，α参数控制分布陡峭度，δ为尺度参数。

假设后向散射信号小波系数wX的先验分布PwX( wX)为正态逆高斯分布，如式(4)所示，斑点噪声的小波系数wN的概率密度函数为

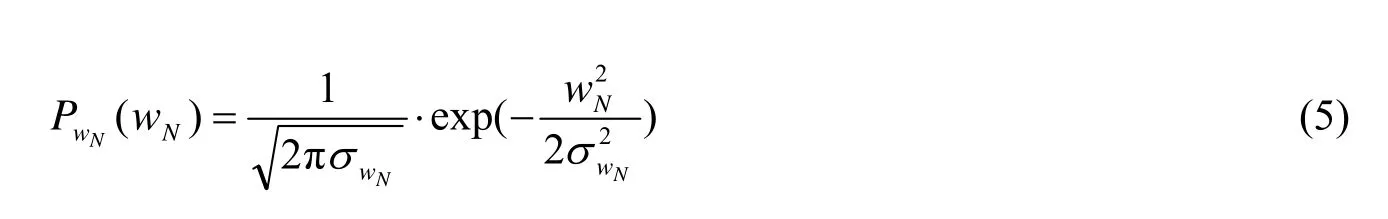
将式(4)、式(5)代入式(3)，参考Hyvarinen的方法[14]，得到：

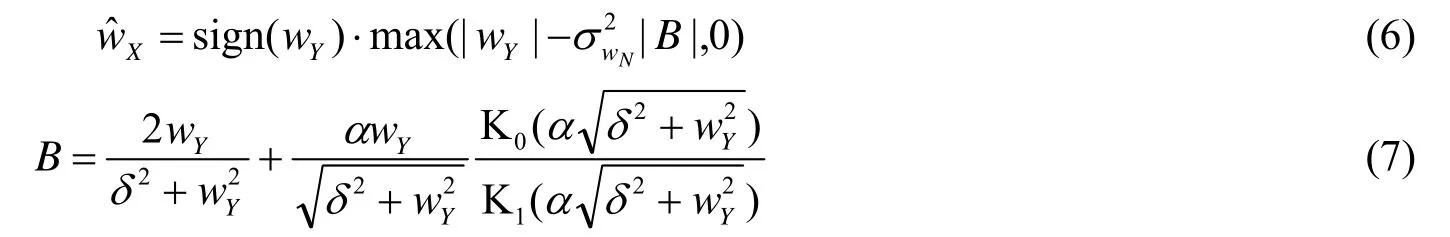
1.2 参数估计

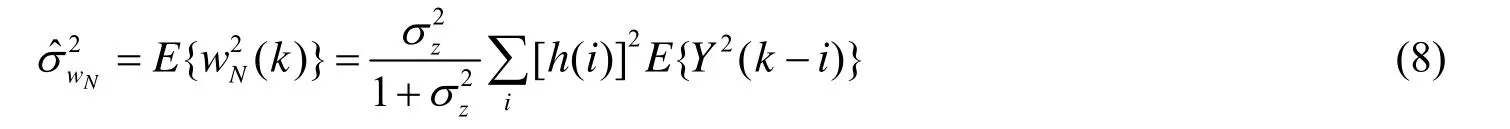
其中：Zσ为乘性噪声标准差，h为小波分解滤波器组中的高通滤波器。

对于正态逆高斯模型，我们采用文献[16]提出的基于二阶累积量的参数估计法。由于该方法又要用到待估计量wX(即无噪图像)，为此，与文献[11]类似，我们先用frost滤波器处理原始SAR图像，得到参考图像，再对其作平稳小波变换，令该信号小波系数为，用此估计正态逆高斯模型的参数。

根据文献[17]，NIG模型的形参α、尺度参数δ的估计表达式分别为

其中：k2、k4分别代表二阶、四阶累积量。k2和k4的统计无偏估计表达式为[18]

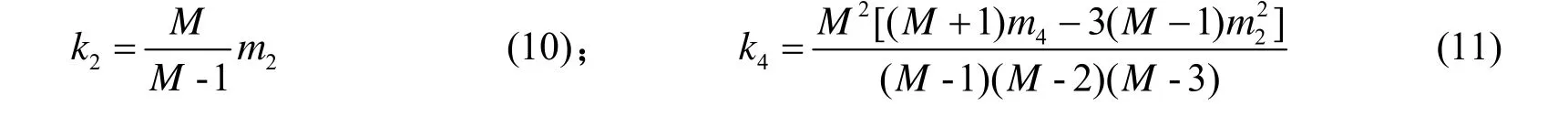
其中：M代表小波系数样本数，m2及m4分别为样本小波系数的2阶和4阶中心矩。

2 异质性测量与分析

2.1 异质性测度及统计分布

SAR图像可以分为同质区域和纹理区域，理想的去斑效果应该是在平滑同质区域的同时保护纹理细节信息，但抑制噪声与保持图像细节两者一般是难以兼得的。一个自然的思路就是将像素划分到不同类别的区域、再采取不同的处理策略[5，11]。异质性反映了SAR图像中不同场景之间图像纹理信息的变化程度，本文选择Argenti等提出的多尺度局部变差系数(MLCV)作为异质度测量指标，以此为依据对小波系数分类，再按类别估计正态逆高斯模型参数，提高模型参数的估计精度。异质度测度定义如下[10]：

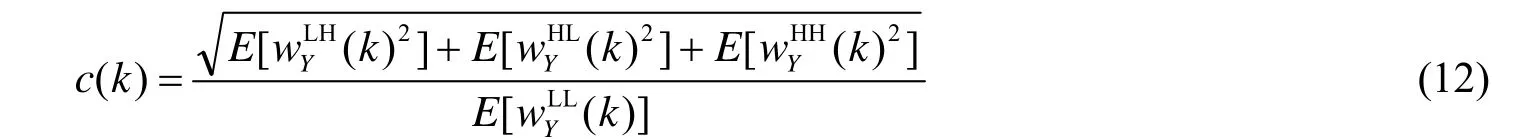
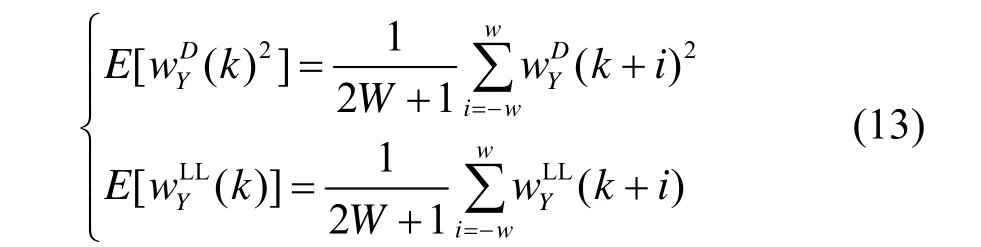
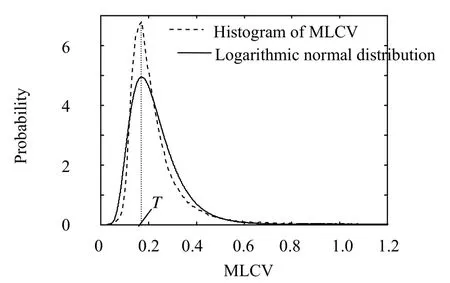
图1 Horsetrack图像第一层子带MLCV经验直方图以及对数正态分布图Fig.1 Histogram of MLCV in the first level of Horsetrack and logarithmic normal distribution pdf

我们统计真实SAR图像异质性测度直方图，发现MLCV呈不对称性分布，先迅速递增到最大值后再逐渐减小，称该最大值所对应的c(k)为模态T。图1给出了Horsetrack图像第一层子带MLCV统计直方图。进一步，考虑到该直方图的非对称性和重拖尾特性，我们提出用对数正态分布对MLCV直方图进行拟合，见图1中的实线部分。从图中可以看出，对数正态分布曲线能够较好的拟合实际的异质性测度直方图，并且由于对数正态分布模型简单，参数估计也很容易得到，因此是一个理想的异质性测度分布理论模型。

2.2 小波系数分类

研究表明，模态T可以作为不同异质性区域分类的依据，当c(k)小于T，其对应位置处像素的异质度偏低；相反则像素异质度则偏高。本文提出将每个小波子带分类为同质区域、若干个异质区域，以及孤立散射点区域，每个系数的分类方法如下：

对于同质区域、以及n个异质区域中的像素，我们假设每类像素分别服从不同参数的正态逆高斯分布，分别估计每一类的NIG参数。对于强异质类区域，相干斑未完全发育，不满足乘性噪声模型(1)，在本文去斑处理中，其值保持不变。

图2显示的是Horsetrack图像第一层子带经过异质性分类，共分了四类，an分别取1、1.5，4。每个子图中的白色区域代表本类像素集合，黑色区域则为其他类像素集合，参考原始真实图像可以发现，(a)图中白色区域对应着原始真实图像中的同质区域，而(b)、(c)、(d)图中白色区域则反映了不同异质度的纹理区域。因此，作为异质性测度指标，MLCV为小波图像分类提供了另外一种有效的手段。

图2 Horsetrack图像第一层子带基于异质性分类图Fig.2 The classification maps of Horsetrack for sub-band in the first level

3 实验结果与分析

为了验证本文算法的有效性，分别对人工加斑图像(即模拟SAR图像)、实际SAR图像进行相干斑抑制实验，主要从滤波效果，边缘保护和量化评估等方面分析讨论。参与的比较实验有：1) 经典的空域ehgamma MAP滤波；2) BayesShrink软阈值去噪算法[19]; 3) 基于NIG的同态滤波[13]，以下简称为“homomorphic-NIG”；4) 基于NIG的非同态滤波，该算法与本文算法的区别在于未采用异质性分类技术，以下简称 “Non-homomorphic-NIG”；实验参数设置如下：ehgamma MAP空域滤波算法的局部窗口尺寸选为5×5；四种基于小波的算法选择4尺度小波分解；本文算法在对小波细节子带进行区域划分时，通过实验我们选取a1=1，a3=1.5，a3=4经验值将每层细节子带分为同质区域，两类异质区域及孤立散射区域四类。

3.1 人工加斑图像

采用对无噪图像人工加斑的方法获得含斑图像，由于有真实的参考图像(即无噪图像)，我们可以获得客观的性能评价指标。对512×512 Lena图像人为加入乘性斑点噪声，产生一幅SNR为13.17的含斑图像。

我们选取四种常用的相干斑抑制指标对上述五种算法做定量评价，包括：信噪比(SNR)，均值(MEAN),等效视数(ENL)和边缘保持指数(EPI)。经上述五种算法处理后图像的视觉效果如图3所示。从图3可以看出，经过ehgamma滤波、BayesShrink算法处理后的图像，还存留了少数的斑点噪声；基于NIG的非同态滤波方法则有所改善。相干斑抑制能力最好的是本文方法和基于NIG的同态滤波方法，与前者(基于NIG的同态滤波方法)相比，本文算法利用了异质性分类技术，兼顾了相干斑抑制与纹理细节的保护，因此处理过的图像更加清晰，得到了满意的去斑效果。

去斑性能实验结果如表1。从表1可以看出，本文算法在上述四个评价指标上均优于其它去斑算法，在去斑能力和保护图像细节的折中方面取得了最好的效果。此外，基于NIG的同态滤波算法没有采用基于异质性的分类技术，但利用统计模型较好的描述了小波系数的分布特性，该算法综合评价指标仅次于本文算法，也取得了较好的效果。

图3 五种算法对仿真SAR图像滤波后的对比Fig.3 Visual comparison of various speckle reduction methods on synthetically speckled image

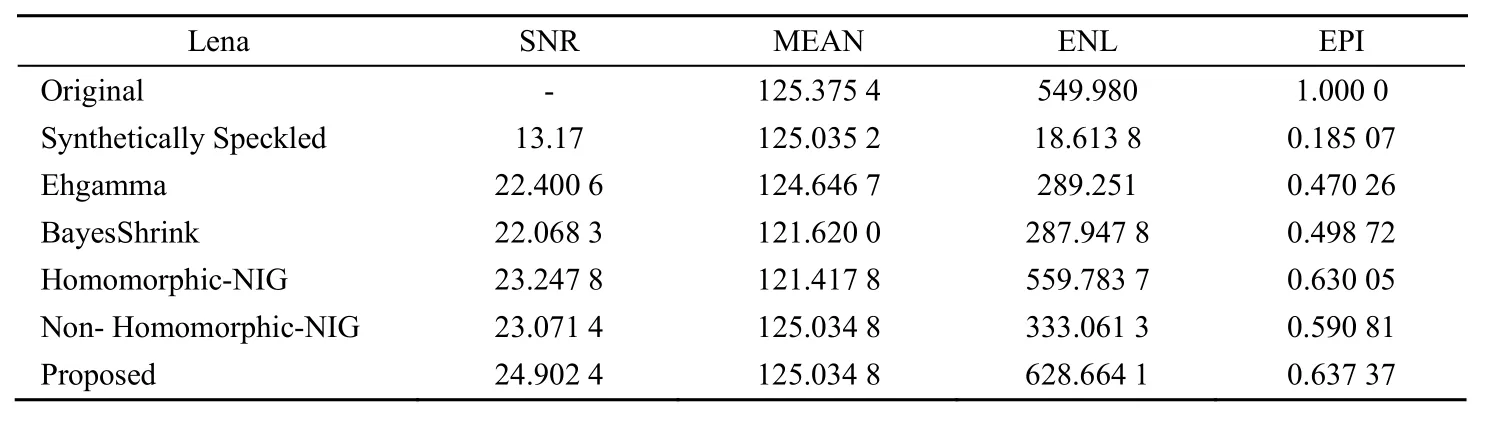
表1 五种算法对仿真SAR图像去斑性能比较Table 1 Performance comparison of 5 methods on synthetically speckled image

3.2 真实SAR图像

对于真实SAR图像，由于无法获得真实的参考图像，因此采用等效视数和均值作为客观评价指标。3幅真实SAR图像选自Sandia National Laboratories，分别为Horsetrack、Agricultural、Pipeline。图4给出了五种算法对Horsetrack图像处理后的视觉效果对比；与前面人工加斑图像实验中的分析类似，从相干斑抑制能力考察，本文方法和基于NIG的同态滤波方法优于其他的方法；但通过观察可以发现，基于NIG的同态滤波方法处理后图像(图4(d))在右上角的纹理区域，相对于本文方法(图4(f))有一定程度的边缘损失，同时本文方法处理后图像的清晰度更高。

图4 五种算法对Horsetrack图像处理后的视觉效果Fig.4 Visual comparison of various speckle reduction methods on real SAR image “Horsetrack”

表2给出了实验结果，从中可看出：1) 本文方法的等效视数均较大于其他四种算法，表现出良好的相干斑抑制能力。2) 从均值考虑，本文方法与原始图像的均值最为接近；本文方法处理后图像的均值与基于NIG非同态滤波几乎相同，明显高于其他算法。

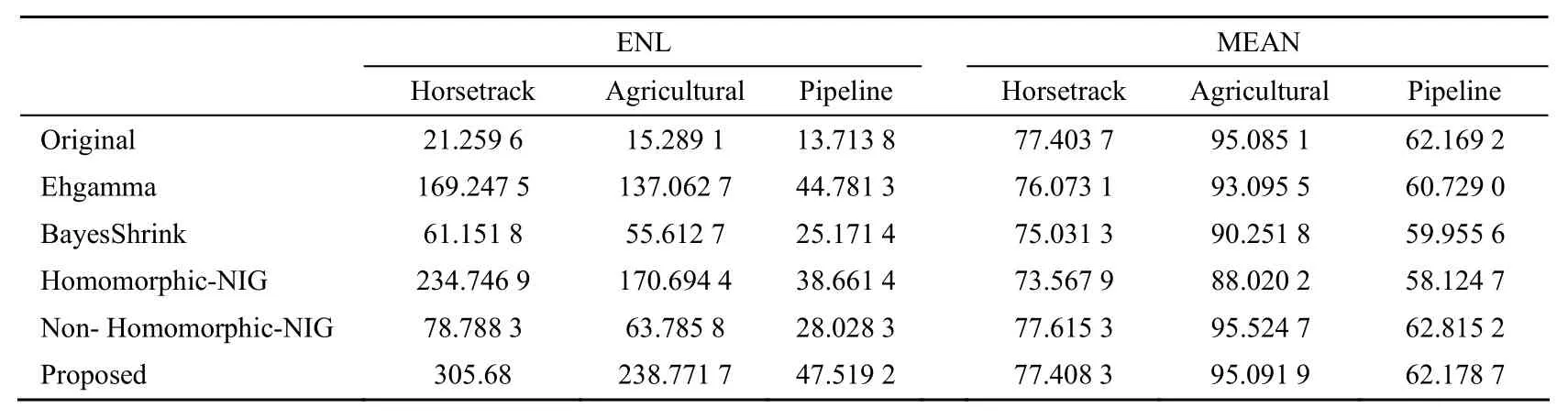
表2 五种算法对真实SAR图像去斑性能比较Table 2 Performance comparison of five methods for real SAR image

4 结 论

本文提出了一种新的SAR图像去斑算法，其本质上属于基于小波统计模型的Bayesian方法。与以往算法不同之处在于：1) 采用了非同态滤波框架，将正态逆高斯函数和高斯函数作为后向散射信号和斑点噪声的先验分布；2) 引入多尺度局部变差系数(MLCV)作为异质度测量指标，研究了MLCV的统计分布特性，提出用对数正态分布对MLCV进行建模；3) 基于异质性测度，将子带中的小波系数划分到具有不同异质性程度的类别，再按照各类别分别估计正态逆高斯模型参数。实验结果表明，该方法不仅利用了小波系数的统计先验知识，还较好的兼顾了边缘细节信息的保护；其中分类估计的方法对提高算法的性能起到了重要的作用。

参考文献：

[1] BHUIYAN M I H，AHMAD M O，SWAMY M N S. Spatially adaptive wavelet-based method using the Cauchy prior for denoising the SAR images [J]. IEEE Transaction on Circuits and Systems for Video Technology(S1051-8215)，2007，17(4)： 500-507.

[2] HOU Jianhua，LIU Xiangming，XIONG Chengyi，et al. Speckle reduction algorithm for synthetic aperture radar images based on Bayesian maximum a posteriori estimation in wavelet domain [J]. Optical Engineering(S0097-3286)，2008，47(5)： 057004-1-057004-11.

[3] FOUCHER S，BÉNIÉG B，BOUCHER J M. Multiscale MAP filtering of SAR images [J]. IEEE Transaction on Image Processing(S1057-7149)，2001，10(1)：49-60.

[4] SOLBØ S，ELTOFT T. Γ-WMAP：a statistical speckle filter operating in the wavelet domain [J]. International Journal of Remote Sensing(S0143-1161)，2004，25(5)：1019-1036.

[5] BIANCHI T，ARGENTI F，ALPARONE L. Segmentation-based MAP despeckling of SAR images in the undecimated wavelet domain [J]. IEEE Transaction on Geoscience and Remote Sensing(S0196-2892)，2008，46(9)：2728-2742.

[6] CHEN Jie，ZHU Jing，LUO Chun-sheng，et al. A novel speckle filter for SAR images based on information-theoretic heterogeneity measurements [J]. Chinese Journal of Aeronautics(S1000-9361)，2009，22(5)：528-534.

[7] LOPES A，TOUZI R，NEZRY E. Adaptive speckle filters and scene heterogeneity [J]. IEEE Transaction on Geoscience and Remote Sensing(S0196-2892)，1990，28(6)：992-1000.

[8] MARTIO BEAUCHEMIN，KEITH P B THOMSON，GEOFFREY EDWARDS. The ratio of the arithmetric to the geometric mean：A first-order statistical test for multilook SAR image homogeneity [J]. IEEE Transaction on Geoscience and Remote Sensing(S0196-2892)，1996，34(2)：604-606.

[9] AIAZZI B，ALPARONE L，BARONTI S. Information-theoretic heterogeneity measurement for SAR imagery [J]. IEEETransaction on Geoscience and Remote Sensing(S0196-2892)，2004，43(3)：619-624.

[10] ARGENTI F，ALPARONE L. Speckle removal from SAR images in the undecimated wavelet domain [J]. IEEE Transaction on Geoscience and Remote Sensing(S0196-2892)，2002，40(11)：2363-2374.

[11] LI Hengchao，HONG Wen，WU Yiyong，et al. Bayesian wavelet shrinkage with heterogeneity-adaptive threshold for SAR image despeckling based on generalized gamma distribution [J]. IEEE Transaction on Geoscience and Remote Sensing (S0196-2892)，2013，51(4)：2388-2402.

[12] BARNDORFF-NIELSEN O E. Normal inverse Gaussian distributions and stochastic volatility modeling [J]. Scandinavian Journal of Statistics(S0303-6898)，1997，24(1)：1-13.

[13] BHUIYAN M I H，AHMAD M O，SWAMY M N S. Wavelet-based image denoising with the normal inverse Gaussian prior and linear MMSE estimator [J]. IET Image Processing(S1751-9659)，2008，2(4)：203-217.

[14] HYVÄRINEN A. Sparse code shrinkage：Denoising of nongaussian data by maximum likelihood estimation [J]. Neural Computation(S0899-7667)，1999，11(7)：1739-1768.

[15] ARGENTI F，BIANCHI T，ALPARONE L. Multiresolution MAP despeckling of SAR images based on locally adaptive generalized Gaussian pdf modeling [J]. IEEE Transaction on Image Processing(S1057-7149)，2006，15(11)：3385-3399.

[16] NICOLAS J M. Introduction to second kind statistic：Application of log-moments and log-cumulants to SAR image law analysis [J]. Traitement Du Signal(S0765-0019)，2002，19(3)：139-167.

[17] BHUIYAN M I H，AHMAD M O，SWAMY M N S. Wavelet-based despeckling of medical ultrasound images with the symmetric normal inverse Gaussian prior [C]// IEEE International Conference on Acoustics，Speech and Signal Processing，Acoustic，France，April 15-20，2007，1：721-724.

[18] FADILI J M，BOUBCHIR L. Analytical form for a Bayesian wavelet estimator of images using the Bessel K form densities [J]. IEEE Transaction on Image Processing(S1057-7149)，2005，14(2)：231-240.

[19] CHANG S G，YU Bin，VETTERLI M. Adaptive wavelet thresholding for image denoising and compression [J]. IEEE Transaction on Image Processing(S1057-7149)，2000，9(9)：1532-1546.

Wavelet SAR Image Despeckling Based on Heterogeneity Classification

HOU Jianhua，CHEN Wen，LIU Xinda，CHEN Shaobo
( Hubei Key Laboratory of Intelligent Wireless Communications, South-Central University for Nationalities, Wuhan 430074, China )

Abstract:A Bayesian wavelet speckle reduction algorithm for SAR image is developed under the non-homomorphic framework. We use Normal Inverse Gaussian (NIG) function for modeling backscattered signal in wavelet domain, and Gaussian function for speckle noise (i.e. signal-dependent noise). The estimation formula of noise-free signal is derived by Bayesian maximum a posteriori (MAP) criterion. With regarding to estimation of model parameters, we introduce Multiscale Local Coefficient of Variation (MLCV) as heterogeneity measure, the histogram of which can be well fitted by logarithmic normal distribution. Based on heterogeneity measure, each coefficient in wavelet sub-band is classified into one of several different heterogeneity scenes, and NIG model parameters are computed in each class through cumulants estimation method. Experiment results show that, compared with its counterpart algorithm in homomorphic framework and its counterpart algorithm in non-homomorphic framework without heterogeneity based classification, our method has obvious advantage in terms of both subjective and objective evaluation, and has obtained satisfactory de-speckled image. A classification method of wavelet coefficients is proposed by heterogeneity measure, which could provide a new means for the research of SAR image despeckling.

Key words:SAR images despeckleing; Normal inverse Gaussian distributiom; heterogeneity measure; classification

作者简介：侯建华(1964-)，男(汉族)，湖北武汉人。博士，教授，主要从事图像处理和计算机视觉方面的研究。E-mail：hou878l@126.com。

基金项目：国家自然科学基金(61141010，61201448)；湖北省自然科学基金(2012FFA113)

收稿日期：2015-03-27； 收到修改稿日期：2015-06-07

文章编号：1003-501X(2016)02-0055-07

中图分类号：TP391

文献标志码：A

doi：10.3969/j.issn.1003-501X.2016.02.010