幺半群ODn的反保序平方幂等元的秩

薛　佳，游泰杰，郭桂容

(1.贵州师范大学数学与计算机科学学院，贵州 贵阳 550001；

2.六盘水师范大学数学系，贵州 六盘水 553004)



幺半群ODn的反保序平方幂等元的秩

薛佳1，游泰杰1，郭桂容2

(1.贵州师范大学数学与计算机科学学院，贵州 贵阳 550001；

2.六盘水师范大学数学系，贵州 六盘水 553004)

[摘要]设ODspan是上的保序与反保序变换半群，证明了当n≥1时，幺半群ODn的反保序平方幂等元的秩为n.

[关键词]保序与反保序变换半群；反保序平方幂等元；秩

1预备知识

设α∈Tn，若α2=α，则称α为幂等元，用E(Tn)来表示Tn中的幂等元的集合；若α2≠α，但α4=α2，则称α是一个平方幂等元，用QE(Tn)表示α中的平方幂等元集合.根据ODn的定义可知，ODn中的变换只有保序变换与反保序变换，从而我们可以把ODn中的平方幂等元分为两类：保序平方幂等元与反保序平方幂等元，分别用符号OQE(ODn)，RQE(ODn)表示.

.

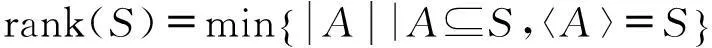
显然h不仅是一个反保序变换，也是平方幂等元，从而可知ODn不能只由保序变换生成，也不能由保序平方幂等元生成.因此，本文将考虑幺半群ODn是可由反保序变换生成，且可由反保序平方幂等元生成，并论证了ODn的反保序平方幂等元秩为

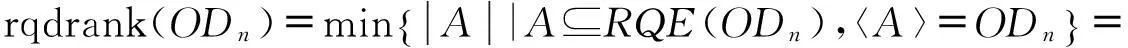
详见本文定理1.

设ODn是幺半群，根据格林等价关系R，L，H和J的定义，可知对任意的α，β∈ODn，

(α，β)∈L⟺im(α)=im(β)，

(α，β)∈R⟺ker(α)=ker(β)，

(α，β)∈J⟺|im(α)|=|im(β)|.

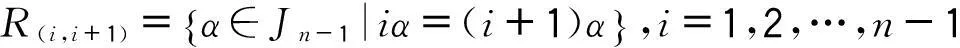
其中J-类中Jn-1有n-1个R-类和n个L-类，且ODn的每一个H-类中只有两个变换，一个保序变换，一个反保序变换.

2主要结论

对于半群中任意的H-类H，设变换α∈H，S是[n]上的一个非空集合，ρ是对[n]的分类.若im(α)=S，ker(α)=ρ，则记含有α的H-类为HS，ρ.若H-类中含有幂等元，则称该H-类为H-类群.

引理1[9]设HS，ρ，HT，σ⊆Ji，1≤i≤n.则HS，ρHT，σ=HT，ρ，当且仅当HS，ρ是H-类群.

由引理1立即可得下面结论.

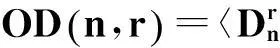
引理4[8]当n≥2时，ODn=〈μ1，μ2，…μn-1，h〉，其中

且有以下关系成立：

(1) h2=1；

(2) hμih=νi，1≤i≤n-1；

(3) μiνj=νjμi，1≤i，j≤n-1，j≠n-i或j≠n-i+1.

引理5ODn中任意一个H-类群中都有反保序平方幂等元.

证明设S是ODn中的任意一个H-类群，即存在一个幂等元e，使得e∈S.又ODn的每一个H-类中有且只有两个元素，一个保序变换和一个反保序变换，又由引理2，存在反保序变换ξ∈S，使得ξ2=e∈S，因此ξ是反保序平方幂等元.

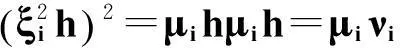
显然由反保序平方幂等元的定义可知α不是反保序平方幂等元.同理可论证当k>i时，α也不是反保序平方幂等元.结论得证.

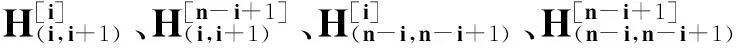
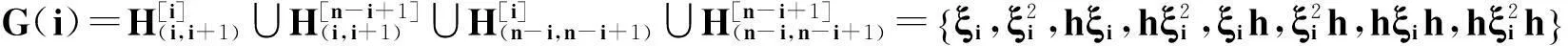
G*(i)=GG(i)，1≤i≤n-1.

为方便，我们引入符号：

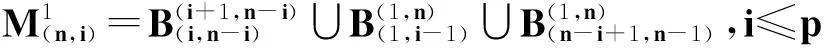
p=n2

引理8设1≤i≤n-1，且.则：

进一步有下面结论成立.

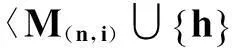
情形1α=β=h.显然αβ=1∉Jn-1.

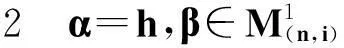
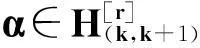
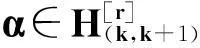
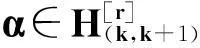
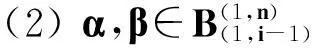
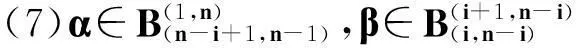
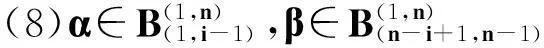
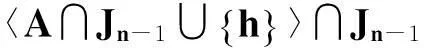
定理1设n≥1，则ODn的反保序平方幂等元秩为n，即rqdrank(ODn)=n.

[参考文献]

[1]GOMES G M S，HOWIE J M. On the ranks of certain semigroups of order-preserving transformations[J].Semigroup Forum，1992，45:272-282.

[2]GARBA G U. On the idempotent ranks of certain semigroups of order-preserving transformations[J].Portugal Math，1994，51:185-204.

[3]UMAR A. On the semigroup of partial one-one order-decreasing finite transformation[J].Proc Roy Soc Edinburgh，1993，123A:355-363.

[4]MADU B A.Quasi-idempotents and quasi-nilpotents in finite transformations semigroups[D]. Zaria：Ahmadu Bello University，1999.

[5]IMAM A T.Subsemigroups generated by quasi-idempotents in certain finite semigroups of mappings[D].Zaria:Ahmadu Bello University，2013.

[6]吴江燕，游泰杰.保序部分变换半群POn的平方幂等元[J].东北师大学报(自然科学版)，2015，47(1):6-11.

[7]FERNANDES V H，GOMES G M S， JESUS M M. Congruences on monoids of order-preserving or order-reversing transformations[J].Glasgow Math J，2005，47：413-424.

[8]FERNANDES V H，GOMES G M S，JESUS M M. Presentations for some monoids of partial transformations on a finite chain[J].Communications in Algebra，2005，33:587-604.

[9]HOWIE J M. Semigroups of mappings[J].Pacific Journal of Mathmatics，2006,37(3)：701-709.

[10]HOWIE J M. Fundamentals of semigroup theory[M].Oxford:Oxford University Press，1995：1-44.

[11]DINITROVA I，KOPPITZ J.On the maximal subsemigroups of some transformation semigroups[J].Asian-European Journal of Mathematics，2008(1)：189-202.

(责任编辑：李亚军)

On the order-reversing quasi-idempotent rank of the monoidODn

XUEJia1，YOUTai-jie1，GUOGui-rong2

(1.School of Mathematics and Computer Science，Guizhou Normal University，Guiyang 550001，China；2.Department of Mathematics，Liupanshui Normal College，Liupanshui 553004，China)

Abstract:Let ODspanbe the order-preserving and order-reversing semigroup on . It is proved that the order-reversing quasi-idempotent rank of semigroup ODspanequals n when n≥1.

Keywords:full order-preserving and order-reversing semigroup；order-reversing quasi-idempotent；rank

[中图分类号]O 152.7[学科代码]110·21

[文献标志码]A

[作者简介]薛佳(1990—)，硕士，主要从事半群代数理论研究.

[基金项目]国家自然科学基金资助项目(11461014)；贵州省自然科学基金资助项目(黔科合J字LKLS[2013]31号).

[收稿日期]2015-05-26

[文章编号]1000-1832(2016)01-0049-05

[DOI]10.16163/j.cnki.22-1123/n.2016.01.012