数据包络分析方法中决策单元偏序关系的建立
木 仁,马占新,文宗川
(1.内蒙古工业大学管理学院,内蒙古 呼和浩特 010051;2.内蒙古大学经济管理学院,内蒙古 呼和浩特 010021)
数据包络分析方法中决策单元偏序关系的建立
木 仁1,马占新2,文宗川1
(1.内蒙古工业大学管理学院,内蒙古 呼和浩特 010051;2.内蒙古大学经济管理学院,内蒙古 呼和浩特 010021)
针对基于偏序集理论的数据包络分析方法中无法给出非规模收益不变模型中决策单元偏序关系的缺陷,提供了三种常见数据包络分析模型中偏序关系的建立理论及偏序关系确定算法。该算法能够给出各个决策单元之间的偏序关系矩阵的同时也能够给出偏序关系图,这为决策者提供了更多的决策依据。最终将这一方法应用到了某省自然科学基金评价问题中。
数据包络分析方法;偏序关系;规模收益;投影
1 引言
数据包络分析方法(Data Envelopment Analysis, DEA)是用于评价具有多投入多产出决策单元效率的方法。在过去三十年期间DEA方法得到了快速的发展与应用[1]。
早期,学者们从不同角度提出了适合不同规模收益情形下的DEA模型——CCR[2],BCC[3],FG[4],ST[5]模型,并将其汇总为了综合DEA模型[6]。然而,这些模型依然不适用于众多实际问题的评价与决策,从而又分别提出了随机DEA模型[7],模糊DEA[8]模型,区间DEA[9]模型,超效率DEA模型[10],广义DEA模型[11],网络DEA模型[12],多阶段DEA模型[13]等。同时对模型的推广及应用方面近期研究工作者们又展开了进一步的研究[14-23]。不难发现这些研究在决策单元投影、决策单元关系的深入挖掘、决策单元的分类与排序、决策单元真实有效的投影方式及逐步改进方式方面的研究依然存在一定的缺陷。
基于建立决策单元特殊关系的目的,早期有马占新首次提出了基于偏序集理论的数据包络分析方法[24],并由木仁等共同对其进行了推广[25-27]。通过建立决策单元之间的特殊关系,进一步完善了决策单元的投影理论。然而,这些方法中仅对规模收益不变的CCR模型进行了研究,对其他DEA模型并未展开深入研究。
本文对规模收益不变,规模收益递减及规模收益递增的三种常见模型CCR、FG及ST模型中引进了决策单元之间的偏序关系,并通过相关定理及其性质,揭示了这一偏序关系的特性,最终通过相关算法给出了决策单元之间的偏序关系矩阵及偏序关系图获取方法。这一偏序关系矩阵及其偏序关系图不仅为决策者提供了决策单元的逐步改进方式,也为决策单元的分类及决策单元关系的确定提供了新的依据,也为规模收益可变DEA模型中决策单元特殊关系的建立提供了相关依据。
2 数据说明及相关定义
假设CCR、ST及FG模型中的DMUi和DMUj的投入产出数据表示为:
Xi=(x1i,x2i,…,xmi)T,Yi=(y1i,y2i,…,ysi)T
Xj=(x1j,x2j,…,xmj)T,Yj=(y1j,y2j,…,ysj)T
假定投入产出的每个分量都大于零,如果存在零或负的投入产出分量,则对所有投入产出数据同时加上某一正数保障所有数据都大于零即可。 此时存在ap(p=1,2,…,m),bh(h=1,2,…,s)使得:
xpi=apxpj,yhi=bhyhj
如果令:
kij=min{a1,a2,…,am},
rij=max{b1,b2,…,bs}
则:
xpi≥kijxpj,yhi≤rijyhj
注:在上述数据中如果对ap,bh没有约束,则所研究结论将适合于CCR模型,如果ap≥1且bh≥1,则所研究结论适合于ST模型,如果ap≤1且bh≤1,则所研究结论适合于FG模型。在文中后续部分我们不再进行相关叙述。
定义1.1 如果a1=a2=…=am=b1=b2=…=bs,则称CCR、ST及FG模型中的DMUi和DMUj是等价的,记为DMUi~DMUj。
定义1.2 如果kij≥rij,则称CCR、ST及FG模型中的DMUi和DMUj存在序关系“”,将其记为DMUiDMUj。
定义1.3 如果kij>rij且kji>rji,则称CCR、ST及FG模型中的DMUi和DMUj存在严格序关系“”,将其记为DMUiDMUj。
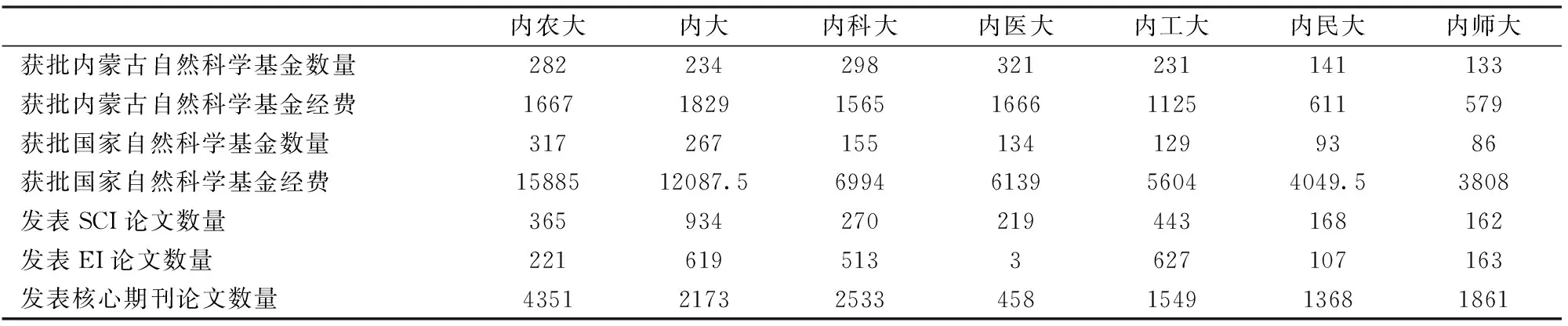
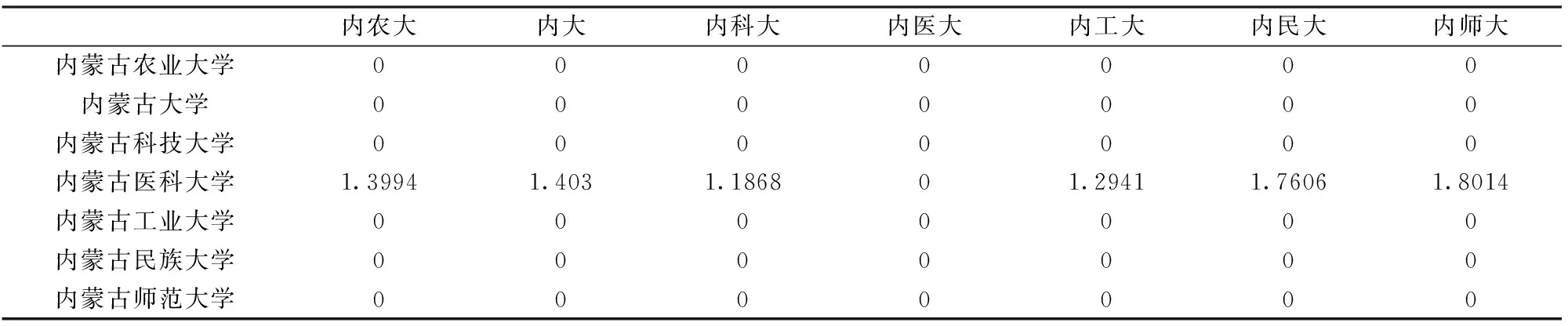
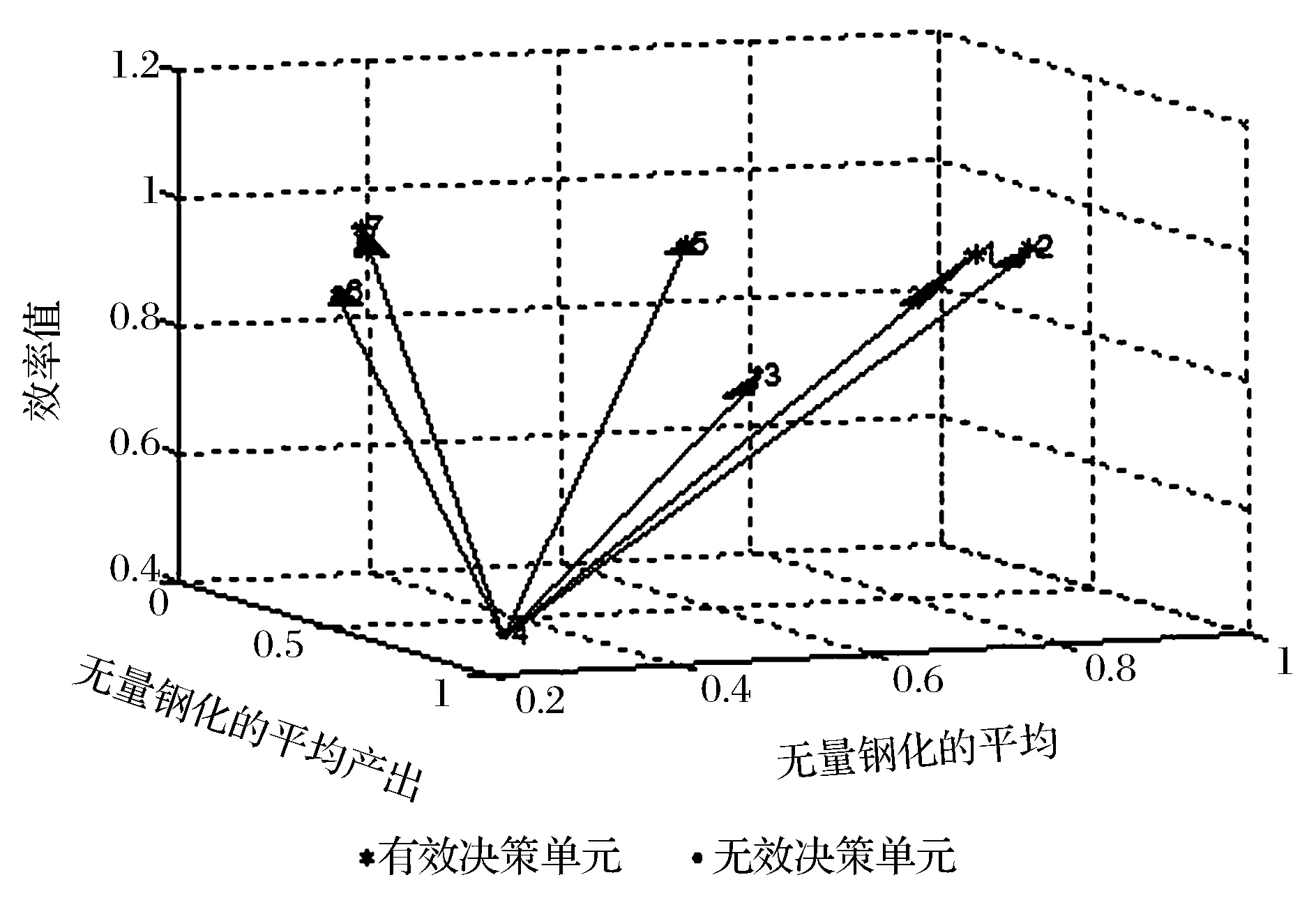
定义1.4 如果kij 定义1.5 设(P,)是一偏序集,x∈P,如果对任意的y∈P,若xy,则必有y=x,则称x为偏序集(P,)的极大元[28]。 定理1.1 定义1.2中引进的CCR、ST及FG模型中序关系“”构成一个偏序集。 证明 根据偏序集的相关定义,对任意的DMUi,DMUj,DMUl(i,j,l=1,2,…,n),需证明自反性,反对称性及传递性。 反对称性:假定DMUiDMUj且DMUjDMUi,需证明DMUi=DMUj。 对于xpi=apxpj,yhi=bhyhj,kij,rij及在ap,bh相应的约束下有: kij≥rij 及其相应约束下有: kji≥rji kji=min{1/a1,1/a2,…,1/am}=max{a1,a2,…,am} rji=max{1/b1,1/b2,…,1/bs}=min{b1,b2,…,bs} xpi≥kijxpj=min{a1,a2,…,am}xpj≥min{a1,a2,…,am}max{a1,a2,…,am}xpi yhi≤max{b1,b2,…,bs}yhj≤max{b1,b2,…,bs}min{b1,b2,…,bs}yhi 于是: min{a1,a2,…,am}max{a1,a2,…,am}≤1 max{b1,b2,…,bs}min{b1,b2,…,bs}≥1 由kij≥rij及kji≥rji得知kijkji≥rijrji,即: min{a1,a2,…,am}max{a1,a2,…,am}≥max {b1,b2,…,bs}min{b1,b2,…,bs} 于是: min{a1,a2,…,am}max{a1,a2,…,am}=1 max{b1,b2,…,bs}min{b1,b2,…,bs}=1 这表明xpi=kijxpj,ypi=rijypj,若kij>rij,即min{a1,a2,…,am}>max{b1,b2,…,bs},则: max{a1,a2,…,am} 即kji kij=rij。 这就证明了DMUi=DMUj。 传递性:如果DMUiDMUj成立且DMUjDMUl,需证明DMUiDMUl。 对于xpi=apxpj,yhi=bhyhj,kij,rij及其ap,bh相应的约束下有: kij≥rij 及其相应约束下有: kjl≥rjl 于是: 令kil=kijkjl,ril=rijrjl,则: kil≥ril 这表明: DMUiDMUl 证毕。 定理1.2 CCR、ST及FG模型中的DMUi是有效的,则DMUi必是CCR、ST及FG模型中的极大元。 证明 假设DMUi是有效的,但DMUi不是极大元,则存在DMUj≠DMUi使得: DMUiDMUj 则对于kij,rij,有: kij≥rij 此时: xpi≥kijxpj,yhi≤rijyhj。 (1)如果kij>rij,则xpi≥kijxpj,yhi 这说明DMUj的效率值要大于DMUi的效率值。从而DMUi的效率值小于1,这与DMUi有效矛盾。 (2)如果kij=rij,则xpi≥kijxpj,yhi≤kijyhj此时由DMUi≠DMUj得知必存在p0或h0使得: xp0i>kijxp0j或yh0i 从而: 这也与DMUi有效矛盾。 定理1.3 CCR、ST及FG模型中如果DMUiDMUj,则DMUi必是无效的。 证明 如果存在一个DMUj,使得: DMUiDMUj 则对于xpi≥kijxpj,yhi≤rijyhj,由于kij>rij,故: xpi≥kijxpj,yhi 此时∀u,v≥0,均有: 即DMUi是无效的。 反之,如果DMUi是无效的,则不一定存在DMUj,使得DMUiDMUj。 定理1.4 CCR、ST及FG模型中DMUiDMUj,且DMUi与DMUj不等价,则DMUi至多是弱有效。 证明 如果DMUiDMUj,则kij,rij,有: kij≥rij 从而: xpi≥kijxpj,yhi≤rijyhj 如果kij>rij,则: DMUiDMUj 根据定理1.3,DMUi是无效的。如果kij=rij,则: xpi≥kijxpj,yhi≤rijyhj 因DMUi≠DMUj,故必存在p0或h0使得: xp0i≥kijxp0j或yh0i≤rijyh0j 从而,对∀u,v>0,必有: 这说明DMUi不是有效的,但如果对任意给定的u,v≥0,我们可通过将某些权重设为零就有可能满足: 这表明DMUi可能是弱有效的。 定理1.2说明了CCR、ST及FG模型中极大元不一定是有效的,那么极大元满足什么条件时必是有效的?以下对CCR、ST及FG模型中的决策单元的相关性质进一步展开分析。 定理1.5 CCR、ST及FG模型中如果两个决策单元DMUi及DMUj之间不存在序关系“”,则存在某两组权重u1,v1≥0及u2,v2≥0使得: 证明 对于: xpi=apxpj,yhi=bhyhj,kij,rij,kji,rji 及满足相应约束的变量有: xpi≥kijxpj,yhi≤rijyhj, xpj≥kjixpi,yhj≤rjiyhi 成立。因DMUi及DMUj之间不存在序关系“”,故DMUiDMUj及DMUjDMUi均不成立。从而: kij 于是: xpi>rijxpj,yhi≤rijyhj, xpj>rjixpi,yhj≤rjiyhi 同理也可取定u2,v2≥0使得: 定理1.5表明,对于不存在偏序关系的两个决策单元存在某一组权重使得一个决策单元的效率值低于另一个决策单元的效率值。 进一步通过定义1.3及定理1.5不难发现CCR、ST及FG模型中的极大元本质上是没有任何决策单元的效率值能够在任何权重下大于等于该决策单元。那么,为什么该极大元有时会是无效的?这是因为决策单元对于其他决策单元的相对优势并不一定能够转化为对所有决策单元的绝对优势。定理1.6对其进行了进一步的说明。 定理1.6 CCR、ST及FG模型中如果DMUi是一极大元,但不是有效的。则对任意满足条件: 的u,v>0,总存在DMUl,使得在该组权重下: 则在改组权重下对任意的决策单元DMUk均有: 成立,这表明DMUi是有效的,矛盾。 定理1.6说明,如果DMUi是一极大元,但不是有效的,则在任何一组权重下DMUi均不能够建立与其他决策单元的绝对优势。 定理1.7 CCR、ST及FG模型中如果DMUi是一极大元,且存在一组权重u,v>0,使得对任意的DMUl,总有: 成立,则DMUi是有效的。 证明 根据定理1.6立即得到证明。 定理1.7表明CCR、ST及FG模型中极大元有效的充分必要条件是该决策单元相对其他所有决策单元具备绝对优势。 单元偏序关系图的绘制 通过定理1.3得知了在CCR、ST及FG模型中有效的决策单元本质上是相应偏序集理论的极大元。为了更加直观地观察出各个决策单元的偏序关系,我们以各个决策单元的效率值为高度,各个决策单元经单位化处理后的平均投入产出数据为横轴和纵轴给出了决策单元偏序关系图绘制算法。算法具体步骤如下: 步骤1:对投入产出数据做无量纲化处理[24]; 步骤2:选定具体模型,并根据定义1.2、1.3及算法给出各个决策单元之间的偏序关系及严格偏序关系; 步骤3:计算各个决策单元的效率值; 步骤4:计算各个决策单元的平均投入数据及产出数据; 步骤5:以各个决策单元的效率值为竖轴,以各个决策单元的平均投入数据及平均产出数据为横轴和纵轴画出各个决策单元的分布图; 步骤6:连接具有偏序关系的各个决策单元,对于具有严格偏序关系的决策单元利用不同直线连接,对于通过传递性可以获取偏序关系的决策单元,不再直接通过直线进行连接。 例1.1表1中给出了“十二五”期间内蒙古七大高校获批内蒙古自然科学基金数量和经费、获批国家自然科学基金数量和经费及发表的SCI期刊论文,EI期刊论文及中文核心期刊论文数量数据。试利用偏序集理论的数据包络分析方法对各大高校进行分析。 解:我们以各大高校获批内蒙古自然科学基金数量和经费为投入数据,以各大高校获批国家自然科学基金数量和经费及发表的SCI期刊论文,EI期刊论文及中文核心期刊论文数量为产出数据对各大高校进行评价。 利用相关算法计算获得CCR模型、FG模型及ST模型中的各个决策单元之间的偏序关系矩阵及偏序关系图。结果表明CCR模型中存在的偏序关系最多,它同时包含了FG模型及ST模型中的偏序关系,但反之并不成立。表2中给出了CCR模型中的偏序关系矩阵,图1中给出了具体偏序关系图,表1及表2中对大学名称进行了缩写,具体大学名称参见表2中的第一列。 在图1中不难发现CCR模型中存在四个有效的极大元,分别是内蒙古农业大学,内蒙古大学,内蒙古工业大学和内蒙古师范大学。两个无效的极大元,分别是内蒙古科技大学和内蒙古民族大学,一个无效的决策单元,是内蒙古医科大学。内蒙古医科大学与所有其他大学之间均存在严格偏序关系,其他决策单元之间并不存在偏序关系。在ST模型中仅存在内医大与内工大、内民大和内师大的之间的严格偏序关系,在FG模型中仅存在内医大与内农大、内大和内科大之间的严格偏序关系。图1中有向箭头表示了不同决策单元之间的严格偏序关系,箭头上方的是较优决策单元。通过上例不难发现不同DEA模型中决策单元之间的偏序关系是不同的。对于上例而言通过近一步的数据分析发现不同高校的学科发展均走向了规模收益递减阶段,即利用FG模型确定其偏序关系是比较合理的。 表1 “十二五”期间内蒙古各大高校获批基金及发表论文相关数据(经费单位:万元) 表2 CCR模型中各大高校偏序关系矩阵 图1 各大高校偏序关系展示图 通过在CCR、ST及FG模型中引进新的偏序关系,提供了规模收益不变、规模收益递增及规模收益递减DEA模型中的决策单元之间的偏序关系。该方法中通过对决策单元进行等比率的放大或缩小之后的投入产出数据比较确定了决策单元之间的偏序关系。同时,基于展示及应用的目的给出了决策单元偏序关系矩阵的获取及偏序关系图展示算法。该矩阵和图更加全面且直观的给出了决策单元之间的偏序关系,这为决策者提供了更为详尽的决策依据。最后,通过相关实例的演示为广大应用者提供了相关方法的应用步骤,也表明了方法具有较强的可推广性及应用性。今后的近一步研究热点是如何确定规模收益可变的诸如BCC模型中的偏序关系,其研究可紧密围绕生产前沿面及数据包络面展开研究。 [1] 马占新,数据包络分析模型与方法[M]. 北京:科学出版社, 2010: 1-17. [2] Charnes A, Cooper W W, Rhodes E. Measuring the efficiency of decision making units[J]. European Journal of Operational Research, 1978, 2(6): 429-444. [3] Banker R D, Charnes A, Cooper W W. Some models for estimating technical and scale inefficiencies in data envelopment analysis[J]. Management Science, 1984, 30(9): 1078-1092. [4] Färe R, Grosskopf S. A nonparametric cost approach to scale efficiency[J]. The Scandinavian Journal of Economics, 1985,87(4): 594-604. [5] Seiford L M, Thrall R M. Recent developments in DEA: The mathematical programming approach to frontier analysis[J]. Journal of Econometrics, 1990, 46(1): 7-38. [6] Charnes A, Cooper W W, Wei Q L, et al. Compositive data envelopment analysis and multiobjective programming[J]. Center for Cybernetic Studies Report, CCS, 1988, 633. [7] Sengupta J K. Data envelopment analysis for efficiency measurement in the stochastic case[J]. Computers & Operations Research, 1987, 14(2): 117-129. [8] Sengupta J K. A fuzzy systems approach in data envelopment analysis[J]. Computers & Mathematics with Applications, 1992, 24(8): 259-266. [9] Entani T, Maeda Y, Tanaka H. Dual models of interval DEA and its extension to interval data[J]. European Journal of Operational Research, 2002, 136(1): 32-45. [10] Andersen P, Petersen N C. A procedure for ranking efficient units in data envelopment analysis[J]. Management science, 1993, 39(10): 1261-1264. [11] 马占新, 唐焕文. DEA 有效单元的特征及 SEA 方法[J]. 大连理工大学学报, 1999, 39(4): 577-582. [12] 评价相对有效性的数据包络分析模型: DEA 和网络 DEA[M]. 北京:中国人民大学出版社, 2012. [13] Coelli T. A multi-stage methodology for the solution of orientated DEA models[J]. Operations Research Letters, 1998, 23(3): 143-149. [14] 王应明, 蓝以信.基于双前沿面数据包络分析的循环全局Malmquist指数[J].中国管理科学, 2015, 23(11): 46-55. [15] 董进全, 邱程程, 马占新, 等. 拟凹生产函数的分区域估计[J] .中国管理科学, 2015, 23(3):32-41. [16] 周忠宝, 丁慧, 马超群, 等. 考虑交易成本的投资组合效率估计方法[J] .中国管理科学, 2015, 23(1):25-33. [17] 李春好, 苏航, 佟轶杰, 等. 基于理想决策单元参照求解策略的DEA交叉效率评价模型[J] .中国管理科学, 2015, 23(2):116-122. [18] 崔玉泉, 张宪, 芦希, 等. 随机加权交叉效率下的资源分配问题研究[J] .中国管理科学, 2015, 23(1):121-127. [19] 张启平, 刘业政, 姜元春. 决策单元交叉效率的自适应群评价方法[J].中国管理科学, 2014, 22(11): 62-71. [20] 雷西洋, 戴前智, 李勇军, 等. 考虑系统内部平行结构的DEA资源分摊方法[J],中国管理科学, 2015, 23(1): 50-55. [21] 石晓,谢建辉,李勇军,等. 非合作博弈两阶段生产系统DEA并购效率评价[J]. 中国管理科学,2015,23(7):60-67. [22] 薛晖,郑中华,谢启伟. 基于多种DEA模型和Gini准则的效率评价方法——兼对我国高校运营绩效的评价[J]. 中国管理科学,2014,22(4):98-104. [24] 马占新, 唐焕文, 戴仰山. 偏序集理论在数据包络分析中的应用研究[J]. 系统工程学报, 2002, 17(1): 19-25. [25] 木仁, 马占新, 崔巍. 基于偏序集理论的数据包络分析方法[J]. 系统工程与电子技术, 2013, 35(2): 350-356. [26] 木仁,李蒙,马占新. 数据包络分析方法中一种新偏序关系确定方法[J]. 内蒙古大学学报(自然科学版),2016,01:1-7. [27] 木仁, 马占新, 长青. 基于格理论的数据包络分析方法[J]. 系统工程与电子技术, 2014, 36(9): 1782-1787. [28] 木仁, 马占新. 决策单元特殊关系的挖掘与建立[J]. 控制与决策, 2015, 30(2): 335-342. The Establishment of Partial Ordered Relations among Decision Making Units in Data Envelopment Analysis Method MU Ren1,MA Zhan-xin2, WEN Zong-chuan1 (1.Management College, Inner Mongolia University of Technology, Hohhot 010051, China;2.School of Economics and Management, Inner Mongolia University, Hohhot 010021, China) Based on the defects that are unable to determine the partial order relations other than constant returns to scale model of the data envelopment analysis method based on partially ordered set theory, a new method and algorithm which determine partial order relations of three different frequently used models are provided. This algorithm can not only give the partial order matrix among the various decision making units but also visualize the results directly, which should provide important decision making information for decision-makers. At last, this method is used in the evaluation of a Provincial Natural Science Fund. data envelopment analysis; partial ordered relation; return to scale; projection 1003-207(2016)11-0103-06 10.16381/j.cnki.issn1003-207x.2016.11.012 2015-09-30; 2016-02-19 国家自然科学基金资助(71401084,71540040);内蒙古自治区草原英才项目(CYYC6006) 文宗川(1973-),男(汉族),内蒙古乌兰浩特人,内蒙古工业大学管理学院,教授,博士,硕士生导师,研究方向:创新方法、评价与决策理论,E-mail:287797817@qq.com. N94;C934 A3 决策单元偏序关系相关定理及其性质

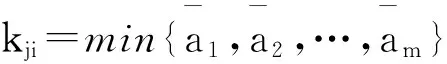

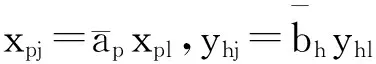



4 决策单元偏序关系确定算法及决策
5 决策单元偏序关系实例
6 结语

