直线电机式主动悬架建模与试验研究*

汪若尘，谢 健，叶 青，孟祥鹏，陈 龙

(江苏大学汽车工程研究院，镇江 212013)

2016080

直线电机式主动悬架建模与试验研究*

汪若尘，谢 健，叶 青，孟祥鹏，陈 龙

(江苏大学汽车工程研究院，镇江 212013)

为实现悬架的主动减振，将直线电机作为汽车主动悬架的作动器。首先建立了1/4车辆主动悬架和直线电机的数学模型，并通过台架试验测试直线电机的输出电磁力，仿真结果与测试吻合较好，验证了直线电机数学模型的正确性；接着采用电流滞环控制和最优控制相结合的方法，根据路面激励状况，控制直线电机作动器输出相应主动力。最后采用dSPACE开发最优控制系统对主动悬架进行了试验。结果表明，所设计的控制系统能有效改善车辆舒适性和行驶安全性。

主动悬架；直线电机；建模；试验研究；电流滞环；最优控制

前言

悬架系统决定车辆乘坐的舒适性和车辆的操纵稳定性。为此，国内外的学者对主动悬架系统的控制方法进行了大量的研究，但是，对主动悬架所用的作动器的研究却较少见。近年来，电磁式主动悬架得到发展，但大多数电磁式的主动悬架需采用旋转电机作为中间转换机构[1-4]，不仅结构复杂，而且控制难度较大。

直线电机式主动悬架以直线电机[5]为作动器具有控制精度高、能量回收率高、无需润滑、结构简单和无需运动转换等优点[6]，受到国内外专家和学者的青睐。

本文中针对直线电机作动器，首先建立了直线电机数学模型和1/4车辆悬架的振动模型，其次采用电流滞环控制和最优控制相结合的方法，设计了直线电机式主动悬架主动力控制系统。通过该控制系统，实现直线电机电磁力的跟踪控制。最后采用dSPACE开发最优控制系统，对直线电机式主动悬架进行台架试验。结果验证了控制系统的可行性，车辆舒适性和安全性得到显著提高。

1 悬架模型和直线电机模型

1.1 主动悬架动力学模型

由于汽车的悬架工作环境比较恶劣，而直线电机又一般用于精度较高的场合，为避免直线电机在悬架振动过程中发生损坏影响工作性能，将直线电机与传统被动悬架中阻尼器和弹簧并联。如果直线电机发生故障，悬架还可以工作于被动模式。

图1 1/4车辆模型

通过对主动悬架动力学分析，建立2自由度1/4车辆模型，如图1所示[7]。图中m2为车身质量；m1为车轮质量；ks为悬架弹簧刚度；kt为轮胎刚度；c为减振器阻尼系数；Ft为直线电机的主动力；x2为车身位移；x1为车轮位移；x0为路面位移。

根据牛顿动力学定律，得到车辆模型的动力学微分方程为

(1)

(2)

路面输入采用有限带宽白噪声为

(3)

式中：f0为下截止频率；w为均值是零的有限带宽白噪声；G0为路面不平度系数；v0为车速。

结合式(1)～式(3),建立主动悬架系统状态方程为

(4)

1.2 直线电机数学模型

在忽略直线电机端部效应和不考虑磁路饱和的前提下,可以得到直线电机在d-q轴模型中的电压平衡方程和运动学方程[8-10]。

d轴电压平衡方程为

(5)

q轴电压平衡方程为

(6)

电磁推力平衡方程为

Ft=K[φfiq+(Ld-Lq)idiq]

(7)

运动平衡方程为

(8)

式中：id，iq，ud，uq，Ld和Lq分别为直、交轴电流、电压和电感，其中Ld=Lq=L=12.78mH；R为电枢电阻，R=10.16Ω；P为极对数，P=2；φf为定子磁钢在电枢中的耦合磁链，φf=0.046Wb；ke为反电动势系数，ke=φfP=64.4V·s/m；ki为推力系数，ki=Kφf=78.9N/A；K为系数，K=3π/2τ(τ为极距，τ=71.2mm)；m为动子和负载的质量，m=5.8kg；v为电机运动相对速度；B为黏性摩擦因数，B=3.7N·s/m；Ft为电磁力；Fn为负载的阻力。当采用磁场定向控制时(id=0)，模型简化为

ud=-LPviq

(9)

(10)

Ft=kiiq

(11)

(12)

2 悬架主动控制

在路面激励下，车辆主动悬架系统会产生受迫振动，通过最优控制器计算出主动控制力，然后通过电流滞环控制直线电机输出电磁力跟踪主动控制力，实现悬架主动控制。图2为主动悬架控制原理图。

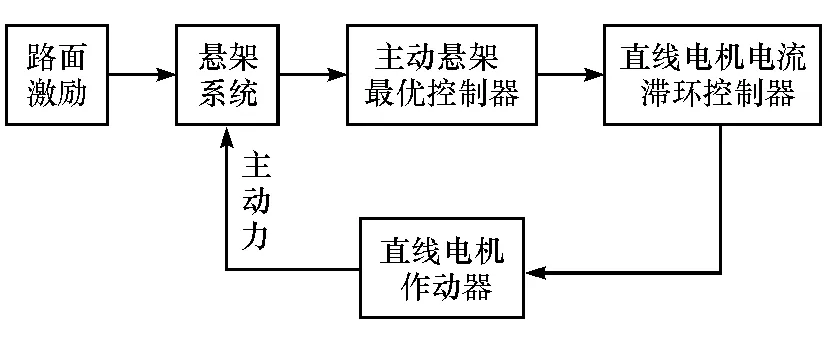
图2 主动悬架控制原理图

2.1 直线电机电流滞环控制

针对直线电机的工作特点，采用控制id=0的磁场定向的电流滞环控制策略[11-12]，来实现励磁电流和推力电流之间的解耦，其原理如图3所示。通过霍尔传感器检测得到ia，ib，ic的测量值，然后将励磁电流id和推力电流iq的参考值经过Park逆变化由旋转的d-q坐标系转换到α-β坐标系，再利用Clark逆变换，转换到a-b-c三相坐标系，得到ia，ib，ic的参考值。最后利用电流滞环比较得到6路PWM信号，从而实现对参考电流的跟踪控制。

图3 永磁直线电机滞环电流控制图

2.2 主动悬架最优控制

汽车悬架系统的性能主要包括车辆平顺性和操纵稳定性。悬架垂向振动加速度越小则车辆的平顺性越好；而要使车辆的操纵稳定性较好，则要保证悬架动行程和轮胎变形量较小。

另外，从经济角度考虑，还应使控制的能量消耗较小[13-15]。将以上因素进行综合，取综合性能指标函数为

(13)

式中：q1，q2，q3和r为加权系数。利用Matlab提供求解代数Riccati方程的lqry函数经过反复试算，求得加权系数：q1=500，q2=5×103，q3=0.5，r=1×10-6。表1为仿真模型参数。

表1 模型参数

3 直线电机模型验证

采用台架实验对直线电机作动器的数学模型进行验证。

图4 直线电机实验台

试验设备:INSTRON 8800数控液压伺服激振试验台(图4)、万用表和三相调压器。

试验过程中，直线电机初级侧通过上夹具用螺栓固定在簧上质量上。次级侧通过下夹具用螺栓固定在激振台上。试验设备通电后，伺服激振台通过液压泵升高到平衡位置，然后，通过三相调压器输入三相交流电，驱动直线电机，激振台上的传感器用于测量直线电机输出的电磁力。

分多次向直线电机输入三相交流电，每个电压下重复两次取平均值。表2为试验结果。

表2 直线电机电磁力

由表2可见，仿真结果相对试验数据的误差在7%之内，说明建立的直线电机模型可靠。

4 仿真结果分析

图5 最优控制力与直线电机电磁力仿真结果

汽车以20m/s车速行驶在B级路面上进行仿真分析，计算得到的最优控制力和直线电机输出的电磁力如图5所示。

由图5可知，最优控制力与直线电机的电磁力曲线基本重合，表明直线电机可根据悬架最优控制力产生所需的电磁力。说明所设计的直线电机电磁力控制系统能有效对直线电机式主动悬架实施跟踪控制。

5 试验研究

台架试验中，根据1/4车辆模型性能评价指标，试验需采集车身加速度信号、悬架动行程信号和轮胎动载荷信号。加速度传感器测得的车身加速度信号和位移传感器测得的悬架动行程信号进入实时数据采集系统。轮胎动载荷信号可由激振头上的力传感器直接获取，数据自动保存在INSTRON 8800数控液压伺服激振试验台的控制计算机上。

对悬架进行试验时，利用MATLAB/Real-Time Workshop/Stateflow Coder将建立的悬架系统和直线电机控制系统仿真模型下载到dSPACE硬件MicroAutobox中。然后通过ControlDesk软件对硬件进行监控和管理，建立虚拟仪表、采集数据、在线调整变量和参数。此时，MicroAutobox起着控制单元的作用，控制模块和控制对象通过硬件I/O实现连接，由此构成闭环系统，给电机驱动器输出PWM信号，实现对直线电机系统的实时控制，达到跟踪目标控制力的效果。在基于dSPACE实时系统对主动悬架进行半实物仿真试验之后，将采集的数据导出，以便分析悬架性能。图6为台架试验图。

图6 台架试验图

在激振台上模拟随机路面输入，分别对被动悬架系统和直线电机式主动悬架系统进行台架试验。悬架系统在车速为20m/s时行驶在B级道路上的响应试验结果如图7和表3所示。

图7 随机激励响应试验结果

悬架类型车身加速度均方根值BArms/(m·s-2)轮胎动载荷均方根值DTLrms/kN悬架动行程均方根值SWSrms/m被动悬架0.82100.61230.0096主动悬架0.64900.50400.0076

由图7和表3可知，车身加速度、轮胎动载荷和悬架动行程分别减小了20.95%、17.69%、20.83%，可见，直线电机式主动悬架改善了车辆的乘坐舒适性。同时，轮胎动载荷大小也有所改善，说明直线电机式主动悬架提高了车辆的行驶安全性。

6 结论

(1) 采用直线电机作为主动悬架的作动器,直线电机特性试验验证了直线电机模型的正确性。所设计的控制系统能够控制直线电机作动器输出相应的电磁力跟踪最优主动力，主动减振效果良好。

(2) 采用dSPACE开发最优控制系统对主动悬架进行试验研究，试验与仿真结果基本吻合，而且试验进一步验证了直线电机式主动悬架的性能要优于被动悬架，为直线电机式主动悬架后续的研究提供了一定的参考依据。

[1] 何仁,陈士安,陆森林.馈能型悬架的工作原理与结构方案评价[J].农业机械学报,2006,37(5):5-9.

[2] 于长淼,王伟华,王庆年.电磁馈能式悬架方案设计与节能分析[J].汽车技术,2010(2):21-25.

[3] 陈宏伟,刘凯.车辆节能型主动悬架的研究[J].农业装备与车辆工程,2008(12):15-18.

[4] 喻凡,曹民,郑雪春.能量回馈式车辆主动悬架的可行性研究[J].振动与冲击,2006,24(4):27-30.

[5] 罗虹,陈星.主动悬架的直线电机作动器控制系统研究[J].系统仿真学报,2012,24(7):1537-1542.

[6] OKADA Y, HARADA H. Regenerative Control of Active Vibration Damper and Suspension Systems[C]. Decision and Control, Proceedings of the 35th IEEE Conference on. IEEE,1996,4:4715-4720.

[7] 黄昆,张勇超,喻凡,等.电动式主动馈能悬架综合性能的协调性优化[J].上海交通大学学报,2009,43(2):226-230.

[8] 张代林,陈幼平,艾武,等.永磁直线电机保证稳态精度的模糊控制[J].电工技术学报,2007,22(4):64-68.

[9] 樊立萍,刘义.直线电机的H∞迭代学习控制设计[J].电力系统及其自动化学报,2009,21(2):87-91.

[10] 翟小飞,张俊洪,赵镜红.永磁同步直线电机的MATLAB仿真及其定位实验[J].船电技术,2006,26(4):6-9.

[11] 邱忠才.直线感应电机控制系统研究[D].成都:西南交通大学,2006.

[12] 伍小杰,罗悦华,乔树通.三相电压型 PWM 整流器控制技术综述[J].电工技术学报,2005,20(12):7-12.

[13] 兰波,刘娇蛟.主动悬架LQG控制器设计[J].系统仿真学报,2003,15(1):138-140.

[14] 艾延廷,王志,甘世俊,等.多自由度车辆模型半主动悬架模糊控制[J].振动与冲击,2007,26(3):19-22.

[15] 唐传茵,李华,周炜,等.基于遗传算法和神经网络的车辆主动悬架控制技术[J].农业机械学报,2009,40(2):6-11.

Modeling and Experimental Study of Active Suspension with Linear Motor

Wang Ruochen, Xie Jian, Ye Qing, Meng Xiangpeng & Chen Long

AutomotiveEngineeringResearchInstitute,JiangsuUniversity,Zhenjiang212013

Linear motor is used as the actuator of vehicle active suspension to realize active vibration attenuation of suspension. Firstly, the mathematical models for both quarter-vehicle active suspension and linear motor are established, and a bench test is conducted to measure the output electromagnetic force of linear motor. The simulation results agree well with test data, verifying the correctness of mathematical model for linear motor. Then by combining current hysteresis control strategy with optimal control scheme, linear motor, as actuator, is controlled to output active force according to road surface excitation. Finally, an optimal control system is developed by dSPACE to test active suspension. The results show that the control system designed can effectively improve the ride comfort and driving safety of vehicle.

active suspension; linear motor; modeling; experimental study; current hysteresis; optimal control

*国家自然科学基金(50905078)、江苏省自然科学基金(BK2012714)、江苏省333工程、江苏省六大人才高峰和江苏省青蓝工程项目资助。

原稿收到日期为2014年10月27日，修改稿收到日期为2015年2月3日。