转矩作用下汽车驱动轴弯曲模态频率的计算方法*

吴昱东，李人宪，向 伟，杨明亮，丁渭平

(1.西南交通大学机械工程学院，成都 610031; 2.荷语鲁汶大学机械工程系，比利时 3001)

2016077

转矩作用下汽车驱动轴弯曲模态频率的计算方法*

吴昱东1,2，李人宪1，向 伟1，杨明亮1，丁渭平1

(1.西南交通大学机械工程学院，成都 610031; 2.荷语鲁汶大学机械工程系，比利时 3001)

为定量研究在转矩作用下，驱动轴弯曲模态频率的变化规律，基于轴向拉力作用下弹性杆的弯曲模态频率计算方法，引入等效拉力的概念，推导出转矩作用下驱动轴弯曲模态频率计算公式，并针对具体车型驱动轴进行计算。结果表明，随着作用转矩的增大，驱动轴1阶弯曲模态频率上升；同时进行了模态测试，计算结果与测试数据基本吻合，说明所提出的计算方法有较好的准确性。

驱动轴；弯曲模态频率；转矩；计算方法；等效拉力

前言

驱动轴是汽车传动系的组成部件之一，不仅承担着将动力传递至车轮驱动车辆前进的作用，而且对车辆的NVH性能有着极其重要的影响。轴向长度较大、直径较小的结构特点导致驱动轴具有较低的弯曲振动模态频率，尤其是其1阶弯曲模态，乘用车驱动轴的1阶弯曲模态频率通常在150～400Hz之间，易被发动机振动激励或驱动轴自身动不平衡激励激发共振，从而加剧传动系齿轮的啮合冲击与驱动轴轴承的振动，严重时会引起车内振动与噪声的显著增大，降低车辆舒适性[1]，因此对汽车驱动轴弯曲模态进行准确的设计有着重要的工程意义。

早期进行驱动轴设计时，并不考虑转矩作用对其弯曲振动模态的影响，然而随着汽车零部件的轻量化发展和材料韧性的提升，承受着巨大转矩(可达2kN·m以上)的驱动轴在工作中会发生较大的扭转变形，这种变形对驱动轴的弯曲模态产生的影响已不容忽视。目前许多汽车整车生产企业已意识到该问题，并明确要求驱动轴生产企业提供汽车驱动轴在零转矩载荷和额定转矩载荷下的1阶弯曲模态频率，以此判断驱动轴的振动特性匹配是否合理。汽车驱动轴生产企业通常利用静扭试验台对驱动轴进行转矩加载，通过试验模态分析方法分别获取驱动轴在零转矩载荷和额定转矩载荷下的1阶弯曲模态频率。然而这种方法需要依赖实物样件作为支撑，且当样件测试结果不满足要求时，由于没有适当的设计计算理论支持，需要根据经验反复进行试制，费时、费力，给汽车驱动轴的开发和生产带来了巨大的阻碍。因此，迫切需要寻求一种考虑转矩作用的驱动轴弯曲模态频率计算方法。

目前，考虑转矩对汽车驱动轴弯曲振动特性影响的研究还较少。但在相邻领域的研究工作中，国内外学者研究了轴向拉力对弹性杆弯曲模态的影响，提出了轴向拉力作用下弹性杆弯曲振动的计算方法[2-5]，并将该计算方法运用于工程中，通过测定弹性杆的弯曲模态频率来预测轴所受的张力[6-8]。弹性杆在轴向力作用下所表现的非线性现象与驱动轴在转矩作用下的非线性振动现象有着较强的相似性，都是由于外力作用改变了轴向张力，引起弯曲平面内恢复力大小的改变，从而对弹性杆或轴的弯曲振动特性产生影响，改变了轴的弯曲模态频率。故本文中基于弹性杆在轴向拉力作用下的弯曲振动力学模型及模态频率计算方法，建立轴在转矩作用下等效力学分析模型，推导转矩作用下驱动轴弯曲模态频率的计算方法，研究转矩对其弯曲振动特性的影响，并以此指导工程中汽车驱动轴的设计工作，提升驱动轴的开发效率与质量。

1 轴向拉力作用下的弹性杆弯曲模态 频率的计算方法

计算弹性杆在两端铰支且受轴向拉力作用下的弯曲模态频率时，首先需要对该弹性杆作如下假设：

(1) 弹性杆在面内振动和面外摆振不具有耦合性，可以看成平面问题来研究；

(2) 振动引起的挠度远小于弹性杆的横向静载挠度，始终处于小变形范围内。

在此基础上，考虑弯曲刚度影响，两端铰支的弹性杆的受力简图如图1所示。

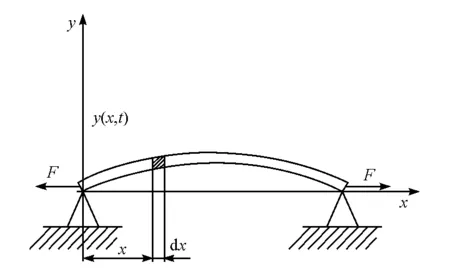
图1 弹性杆受轴向拉力作用时的力学简化模型

由结构动力学原理可建立弹性杆在平面内的微分振动方程为

(1)

式中：E为轴或弹性杆的材料弹性模量，GPa；I为轴或弹性杆的惯性矩，m4；x为沿弹性杆轴向的坐标，m；y为弹性杆的径向振幅，m；F为弹性杆的轴向拉力，kN；m为轴或弹性杆的线密度，kg/m。

在两端铰支的边界条件下，由式(1)可求得弹性杆弯曲模态频率的计算公式[9]为

(2)

2 转矩作用下轴的等效拉力计算

由于转矩作用下轴的非线性振动现象与轴向拉力下的弹性杆相似，都是由于轴向张力改变，导致弯曲平面内恢复力变化而引起的。因此，首先要对转矩作用下的轴进行准确的受力分析，求取引起其轴向张力改变的等效拉力，再根据轴向拉力作用下弹性杆的弯曲模态频率计算方法，推导转矩作用下轴弯曲模态频率的计算方法。

图2为一等直径实心圆轴在转矩作用下的力学模型示意图，图2(a)为该圆轴原始状态，同样须对其进行假设：

(1) 圆轴材料各向同性且分布均匀；

(2) 圆轴在弯曲平面内振动和面外摆振不具有耦合性，可以看成平面问题来研究；

(3) 振动引起的挠度远小于圆轴的横向静载挠度，始终处于小变形范围内；

(4) 圆轴在转矩作用下处于线性形变区间。

如图2(a)和图2(b)所示，沿圆轴的轴线方向，取长度为l，横截面积为dr×ds的微杆单元，此处，dr和ds分别为沿径向和周向的增量。当该等直圆轴受到转矩M作用时，该杆单元长度被拉伸至l′，如图2(c)所示，则可得该杆单元所受等效拉力为

(3)

图2 力学模型示意图

式中：r为微杆单元所在位置与轴心线的距离，m；l为轴的长度，m；φ为轴的扭转角位移，rad。

设处在与轴心线距离为r的所有杆单元(它们构成半径为r的薄壁圆管单元)受到的拉力和为dTr，则

(4)

根据式(4)，在[0，R]区间内进行积分(R为轴截面半径，m)，可求得该圆轴所受的等效总拉力为

(5)

(6)

式中：M为轴所受到的转矩，N·m；G为轴材料的切变模量，GPa；Ip为轴的极惯性矩，m4。

将式(6)代入式(5)中，可得到等效总拉力T与轴受到转矩M的关系为

(7)

当转矩M≠0时，式(7)积分结果，即圆轴在转矩作用下的等效拉力为

(8)

同理可推得当转矩M≠0时，空心轴管在转矩作用下的等效拉力为

(9)

式中：R0为轴管外圆半径，Ri为轴管内圆半径。

3 转矩作用下驱动轴的弯曲模态频率 计算方法

将转矩作用下轴所受的等效拉力T代入式(2)，则可获得圆杆在转矩作用下的弯曲模态频率：

(10)

其对应的弯曲模态频率为

(11)

将式(8)代入可得M≠0时实心圆轴的1阶弯曲模态频率计算公式为

(12)

同理，将式(9)代入式(11)即可得到转矩作用下空心轴管弯曲模态频率的计算公式，这里就不再赘述。

4 计算方法验证

为验证上面推导的转矩作用下轴弯曲模态频率计算公式的有效性，针对某前置前驱轿车驱动轴，进行弯曲模态的测试。将驱动半轴安装于驱动轴静扭试验台上，如图3所示，运用“游动锤击法”进行模态测试，通过静扭试验台改变驱动半轴两端所受转矩，分别测取驱动半轴在不同转矩下的1阶弯曲模态频率。

图3 驱动半轴静扭试验台

该轿车驱动轴额定转矩约为2kN·m，通过“游动锤击法”测试获取0～2kN·m转矩范围内驱动半轴的1阶弯曲模态频率；利用式(12)计算得到驱动半轴在0～2kN·m转矩作用下，1阶弯曲模态随转矩增大的变化曲线，并将计算分析结果与测试结果进行对比，如图4所示。

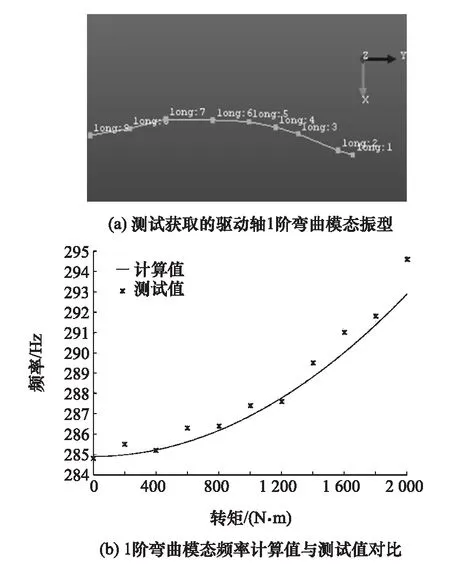
图4 驱动轴试验模态分析及计算模态分析结果

图4(a)为“游动锤击法”测试获得的驱动轴1阶弯曲模态振型；图4(b)为不同转矩下1阶弯曲模态频率计算值与测试值的对比。可以看出，计算结果与测试结果较好地吻合，相对误差不超过3%，测试值总体要比计算值略大。误差产生的原因主要有两个：(1)实际中轴的材料、约束与数值计算时所使用的参数存在差异；(2)数值计算结果本身存在误差，这从转矩为零时计算值与测试结果的差异可以看出。在实际使用时，可以通过精确核实轴系材料参数、结构尺寸和约束关系，进一步提高计算结果的精度。另外，从图4(b)还可看出，随着两端所受转矩载荷的增大，驱动轴1阶弯曲模态频率逐渐升高，载荷从0增至额定值2kN·m，1阶弯曲模态频率增幅达10Hz左右，驱动轴1阶弯曲模态频率改变对车辆传动系甚至整车的中低频NVH性能都将造成不可忽视的影响。

5 结论

(1) 推导了转矩作用下轴的弯曲模态计算方法，并设计针对性实验对该计算方法进行了验证，结果表明，该计算方法较为准确，计算结果与实际驱动轴振动特性吻合，可以有效用于转矩作用下汽车驱动轴的弯曲模态频率的计算与分析。

(2) 汽车驱动轴所承受的外部转矩会对其弯曲振动特性产生影响，在线性形变区间内，随着外部转矩的增大，驱动轴的1阶弯曲模态频率升高。

[1] BIERMANN, J W. Impact of Side Shaft on the Interior Noise of Cars[C]. International Conference on Noise and Vibration Engineering, Vols 1-8,2005:3343-3352.

[2] NAGULESWARAN S. Vibration and Stability of an Euler-Bernoulli Beam with up to Three-step Changes in Cross-section and in Axial Force[J]. International Journal of Mechanical Sciences,2003,45(9):1563-1579.

[3] REDDY J N. Nonlocal Theories for Bending, Buckling and Vibration of Beams[J]. International Journal of Engineering Science,2007,45(2):288-307.

[4] 孟浩,刘耀宗,王宁,等.轴向力对轴系弯扭耦合振动特性的影响[J].振动与冲击,2008(10):103-105.

[5] 邢静忠,柳春图.刚性土壤上含有轴向力的悬跨管道的静弯曲和固有频率[J].工程力学,2011(12):87-91.

[6] 任伟新,陈刚.由基频计算拉索拉力的实用公式[J].土木工程学报,2005(11):26-31.

[7] 方志,汪建群,颜江平.基于频率法的拉索及吊杆张力测试[J].振动与冲击,2007(9):78-82.

[8] 何伟,陈淮,王博,等.复杂边界条件下基于频率法的吊杆张力测定研究[J].土木工程学报,2012(3):93-98.

[9] ROY R, CRAIG Jr.结构动力学[M].常岭,李振邦,译.北京:人民交通出版社,1996.

Calculation Method for the Bending Modal Frequency ofVehicle Drive Shaft Under the Action of Torque

Wu Yudong1,2, Li Renxian1, Xiang Wei1, Yang Mingliang1& Ding Weiping1

1.SchoolofMechanicalEngineering,SouthwestJiaotongUniversity,Chengdu610031；2.DepartmentofMechanicalEngineering,KULeuven,Belgium3001

The changing law of the bending modal frequency of drive shaft under the action of torque is studied in this paper. Based on the calculation method for the bending modal frequency of elastic bar under the action of axial tension force with a concept of equivalent tension force introduced, the formula for the bending modal frequency of drive shaft under the action of torque is derived, and the calculation for the drive shaft of a specific vehicle is conducted. The results show that with the increase of the torque applied, the first order bending modal frequency of drive shaft rises. Meanwhile a corresponding modal test is also performed, and the above simulation results well agree with test data, demonstrating the correctness of the calculation method proposed.

drive shaft; bending modal frequency; torque; calculation method; equivalent tension force

*高等学校博士学科点专项科研基金项目(20100184110002)和中央高校基本科研业务费专项资金(SWITU12CX036)资助。

原稿收到日期为2014年11月24日，修改稿收到日期为2015年2月4日。