基于LTV-MPC的车辆稳定性控制研究*
陈 杰,李 亮,宋 健
(清华大学,汽车安全与节能国家重点实验室,北京 100084)
2016050
基于LTV-MPC的车辆稳定性控制研究*
陈 杰,李 亮,宋 健
(清华大学,汽车安全与节能国家重点实验室,北京 100084)
针对含有附着力约束和液压执行机构约束的车辆稳定性控制问题,本文中提出了一种基于非线性车辆模型的线性时变模型预测控制(LTV-MPC)方法。该方法对非线性车辆模型进行局部线性化,结合实时参数估计得到的纵向制动力输入限制,将该问题转化为二次规划问题,并得到优化解,从而解决有约束条件下的主动制动压力分配问题。另外,文中还讨论了MPC控制器中控制目标的选取问题,分析了控制参数选取对于控制效果和运算效率的影响。通过稳态和瞬态仿真验证了控制器的可行性和有效性。
车辆动力学;模型预测控制;稳定性控制
前言
车辆稳定性控制(ESC)系统能够提升车辆在非线性工况下的稳定性,大幅度降低交通事故发生率[1]。基于差动制动方式的ESC控制方法在线性和非线性工况下都能比较有效地对车辆施加横摆力偶矩[2],是目前被普遍采用的一种方案。ESC系统控制方法和主动制动力分配策略是车辆稳定性控制中的重要课题。
针对ESC系统的控制策略,许多学者进行了相关的研究。早期的一些研究提出了基于逻辑门限的ESC控制方法[3],该方法利用固定的约束条件保证了系统的稳定性,但控制输入较为粗暴,且逻辑门限的设定需要丰富的实车试验经验以及复杂的标定工作。基于二次调节器(LQR)形式的最优控制方法也在ESC控制中得到了较好的应用[4-5],该方法理论上可以得到优化问题的全局最优解,但由于控制器模型采用2自由度线性模型,模型失配会导致求得的解并不能达到最优控制的理想效果。另外基于车辆2自由度模型的最优控制问题也只能近似地转化为LQR问题进行求解,两者的差别在低非线性度工况下很小,但在高非线性度的极限工况下较大,也导致控制效果与理论上有一定的差距。另外还有滑膜控制[6]、相平面法[7]等各种方法也都在ESC中得到了不同程度的应用。
模型预测控制(MPC)是一种在工业生产领域得到广泛应用的先进控制方法。该方法采用滚动时域优化的方法预测未来一段时间内系统状态并求取使目标函数最小的控制输入。模型预测控制相比于LQR最优控制虽然不能求得全局最优解,但由于每个周期都基于系统参数的观测量进行预测和求解,更加适用于无法得到精确模型的实际应用,而且也可以得到问题的次优解。模型预测控制的主要缺点在于控制器运算量较大,在高频控制问题中实时性较难保证,故多应用于低频的工业控制如造纸、炼油等领域中。但随着车用芯片运算能力的提高和对控制问题的合理简化,模型预测控制在车辆控制领域也逐渐得到了应用。文献[8]中设计了用于车辆自动驾驶控制的模型预测控制器,但该问题的车辆行驶路径是预先设定的,与ESC控制有所区别。文献[9]中设计了基于模型预测控制的主动避撞分层控制方法,但它仅限于上层横摆力矩控制器的设计。文献[10]中将模型预测控制运用于主动转向问题中,取得了较好的效果。文献[11]中首次研究了基于模型预测控制的差动制动控制问题。文献[12]中对模型预测控制在车辆控制领域的应用进行了较为全面的讨论。
本文中建立了线性时变模型预测ESC控制器,得到带有约束的ESC问题优化求解方法。讨论了考虑车辆动态响应特性的横摆角速度和车身侧偏角目标值的选取方法。分析了MPC控制器参数对于控制效果的影响。对所设计的控制器进行了稳态和瞬态的仿真验证并与传统的LQR控制器进行对比,得到了较好的控制效果。
1 车辆动力学模型
模型预测控制器对于模型的准确性有一定的要求,如果模型失配严重,预测得到的系统状态将会与实际状态有较大的偏离,从而影响控制效果。采用线性轮胎模型的2自由度的车辆模型没有考虑到车辆轮胎的非线性特性,而横摆力矩控制起作用的大部分工况中车辆轮胎都处于非线性区域,故模型预测控制器中的预测模型需要采用较为准确的非线性形式。将车辆质心侧偏角和横摆角速度作为系统变量,车辆侧向运动的动力学方程为
(1)
式中:m为整车质量;vx为车辆纵向速度;δ为前轮转角;ωz为车辆横摆角速度;Iz为车辆绕垂直轴的转动惯量;w为轮距;a为质心距前轴的距离;b为质心距后轴的距离;Fxij,Fyij(ij=11,12,21和22,分别为左前,右前,左后和右后)为轮胎纵向力和侧向力。式中的轮胎力利用魔术公式(Magic Formula)形式的轮胎模型进行计算[13]:
(2)
其中:
Cx=b0;Cy=a0
Dx=b1Fz2+b2Fz;Dy=a1Fz2+a2Fz

Ex=b6Fz+b7Fz+b8;Ey=a5Fz+a6
式中ai(i=0,…,6)和bj(j=0,…,8)为通过试验测得的参数,具体取值如表1所示。

表1 轮胎魔术公式模型参数
式(2)所示的轮胎模型表示的是单一方向的轮胎力,即轮胎侧偏角为0和轮胎滑移率为0时的轮胎力,在既存在滑移率又存在侧偏角的联合滑移工况还需要进行一定的修正,按照文献[13]中推荐的方法,对联合滑移工况进行修正:
(3)

式中:λ为滑移率;α为轮胎侧偏角。
在仿真试验中假设车辆纵向速度、车轮转速、车辆侧向加速度和横摆角速度为可测量的量;车身侧偏角和路面附着系数须通过估算得到;而车轮的侧偏角和垂直载荷则须利用测量和估算的变量计算得到:
(4)
(5)
由于上述系统动力学方程中包含形式复杂的轮胎模型,导致将此模型用于控制器时无法写成矩阵形式的状态方程,必须采用数值方法进行控制器求解。非线性模型预测控制的数值求解需要运用序列二次规划法和粒子群算法等复杂的数值求解技术,这将大大增加控制器的复杂程度并降低控制求解速度。因此,本文中采用局部线性化的方法将非线性模型预测控制问题转化为线性时变参数的模型预测控制问题。
假设当前测量和观测得到的车辆状态为ε0,轮胎侧偏角为α0ij,将轮胎侧向力线性化为
(6)
将式(6)带入式(1)得到线性化的系统状态方程为
(7)
式中:x为系统变量,x=[βωz]T;Ac为状态矩阵;u为控制输入,u=[Fb11Fb12Fb21Fb22]T,即4个车轮的制动力;Bcu为控制矩阵;e1为轮胎纵向力与轮胎制动力之差,视为可测干扰输入,Nc1为其对应的干扰输入矩阵,Nc1=Bcu;e2为前轮转角,也视为可测干扰输入,Nc2为其对应的干扰输入矩阵。
2 模型预测控制器
本文中采用的控制策略如图1所示,该控制器包含路面附着系数估计、侧偏角估计、垂直载荷估计、轮胎力估算等观测模块,目标值计算模块实时给出系统变量目标值,控制约束计算模块则实时计算制动力和制动力增量的上限。MPC控制器直接给出各轮主动制动力,经过滑移率控制器判断轮胎的滑转或抱死程度后得到主动制动压力作用于车辆。
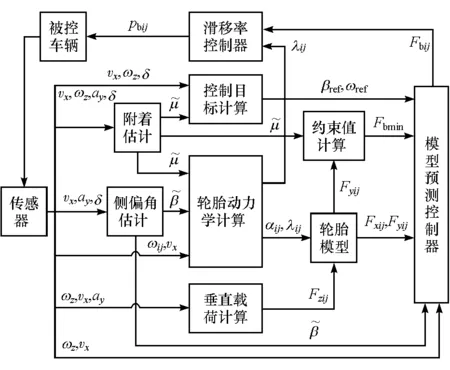
图1 整体控制策略
2.1 模型的离散化
在实际应用中,控制器以一定的周期运行,所以首先将连续时间系统的模型转换为离散时间系统的模型来构建控制器。将系统的离散方程写为
(8)
其中: Δx(k)=x(k)-x(k-1)
Δu(k)=u(k)-u(k-1)
Δe1(k)=e1(k)-e1(k-1)
Δe2(k)=e2(k)-e2(k-1)
式中yc为系统输出。
与式(7)连续模型对比,各矩阵的关系为
(9)
式中:Ts为控制器周期;eAct为连续系统的状态转移矩阵。
2.2 线性时变模型预测控制器的设计
模型预测控制的基本思想是,根据当前观测到的系统状态预测未来一定时间内的系统状态并求解在此时间域内使控制目标最小的控制输入。本文中的模型预测控制器选择的预测时域p=2,控制时域m=2,并做如下两个假设:
(1) 控制时域之外,控制量保持不变,即
Δu(k+i)=0,i=m,m+1,…,p-1
(10)
(2) 可测干扰在当前时刻之后不变,即
Δe1(k+i)=Δe2(k+i)=0,i=1,2,…,p-1
(11)
根据式(8)可以预测未来p步的系统输出为
Yp= SxΔX(k)+IYd(k)+SuΔU(k)+
Sd1Δe1(k)+Sd2ΔE2(k)
(12)

式中Yp为在k时刻预测的未来p=2个时刻的系统输出。控制目标函数选为
J=‖Gy(Yp(k)-R(k+1))‖2+‖GuΔU(k)‖2
(13)
式中:Gy=diag{gy1,gy2}为控制输出的加权矩阵;Gu=diag{gu1,gu2}为控制输入的加权矩阵;R(k+1)=[r(k+1)r(k+2)]T为未来p=2个周期的控制输出期望值,r(k)=[βref(k)ωref(k)]T;ΔU(k)=[Δu(k) Δu(k+1)]T是控制输入增量序列,也是控制优化问题的独立变量。求解的问题是:在满足式(8)系统动力学方程和式(14)约束的条件下寻找使式(13)目标函数最小的控制输入ΔU(k)。
(14)
式(14)中包含了对四轮制动力的约束和四轮制动力增量的约束。由于在车辆运动过程中轮胎力会随车辆状态发生变化,故制动力和制动力增量的约束必须根据车辆运行状态进行实时计算。制动力主要受到路面附着力的约束,施加于车轮的制动力应该保持在附着力范围之内以防止车轮抱死。文献[14]中曾经指出,当轮胎侧向力达到附着力极限时,轮胎在纵向还存在可观的纵向力余量可以施加主动制动。从轮胎力的附着椭圆上也可以看出轮胎的纵向力和侧向力极限轨迹并非是一个圆,而是一个椭圆,纵向力的极限大于侧向力极限[13]。因此,可以将轮胎纵向制动力极限设定为如下形式:
(15)
式中ρ取0.8。
由于液压执行机构的限制,每个周期控制增量也有一定的限制,根据增减压试验标定可以确定每个周期主动制动的增减压速度极限,从而确定Δumax。
如图1所示,在每个控制周期中,观测器根据车辆传感器及观测器得到的路面附着系数、车轮滑移率、车身侧偏角、车轮垂直载荷等信息利用轮胎模型计算得到车轮侧向力,然后根据式(15)和标定的增减压限值得到制动力和制动力增量的上下限值。由式(8)和式(14)的线性形式,可将式(13)目标函数和式(14)约束方程做适当变形即可将该问题化为线性二次规划(LQP)问题进行求解,限于篇幅推导过程从略。
2.3 滑移率控制器设计
由于上层模型预测控制直接得到了主动制动力,经过比例换算即可得到制动压力,故下层控制器只须对车轮的滑移率进行一定的限制即可。虽然有式(14)所示的控制输入约束保证控制器施加的制动力不会过大,但是由于路面附着系数估算、载荷转移估算等环节可能存在误差,还需要滑移率控制器对车轮的滑移率进行进一步的控制,保证避免出现车轮抱死或完全滑转的情况。滑移率控制器的控制逻辑如图2所示。

图2 滑移率控制器逻辑
2.4 控制目标的确定
(1) 目标横摆角速度
目标横摆角速度体现了驾驶员对于车辆横摆角速度对转角输入的响应的预期。由于车辆大部分时间工作在线性响应区域,驾驶员的经验也来源于此,所以ESC控制器中一般将横摆角速度的目标值设为2自由度自行车模型的横摆角速度响应值[15]。
(16)

路面附着力限制了车辆可以达到的侧向加速度上限,车辆的侧向加速度可以表示为
(17)
式中的第1项通常较小,按照文献[16]中的结论,第2项应该占到侧向加速度极限的85%,从而可以将横摆角速度极限表示为|ω|max=0.85μg/vx。经过此上限限制,横摆角速度目标值修正为
(18)
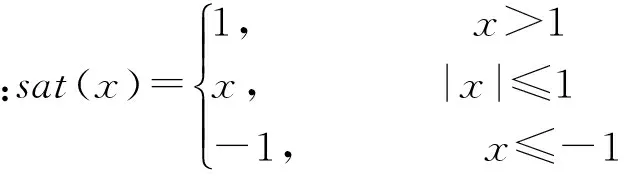
式中sat(x)为截止函数。
由于车辆存在惯性,横摆角速度对于转向盘转角的响应存在一定的过渡过程,这一过渡过程也包含在驾驶员的期望当中,如果按照式(18)的方式设计横摆角速度目标值,势必存在过渡过程中的过度干预和之后的超调,故须在横摆角速度目标值上增加延迟环节,本文中采用一个1阶滞后环节来近似这个过渡过程:
(19)
在过渡过程中,横摆角速度的响应还存在一定的超调,少量的超调符合驾驶员的预期,而且只要车身侧偏角在一定范围内,也不会引起车辆失稳。如果仅按照式(19)的方式计算横摆角速度目标值,当横摆角速度发生少量超调时也会引起不必要的控制。故对ωref2进行进一步的调整,适度引入横摆角速度的超调量,得到最终的目标横摆角速度为
(20)
(2) 目标车身侧偏角
在ESC控制的研究中有两种常见的目标车身侧偏角设置方法:一种是,许多研究认为驾驶员始终希望面向车辆速度方向,故将目标车身侧偏角设为0[17],这种方法符合驾驶员的期望,侧偏角为0也是车辆的稳定状态,但在实际车辆中很难实现,特别是在低速大转向和高速大转角的情况下,将目标车身侧偏角设为0容易引起不必要的频繁控制;另外一种是,有些研究为了避免这样的问题,将2自由度车辆模型的稳态侧偏角响应作为目标车身侧偏角,即认为2自由度车辆模型的响应特性符合驾驶员的期望[18],这种方法取得的目标侧偏角比较符合车辆运动的实际情况。本文中采用第2种方法确定目标车身侧偏角。
按照2自由度车辆模型可以得到车辆的稳态侧偏角响应为
(21)
与横摆角速度类似,目标车身侧偏角也需要加入动态修正。由2自由度车辆模型可以推导出车身侧偏角的响应为一个2阶滞后系统,即
(22)
为了避免不必要的频繁控制,需要给车身侧偏角设置一个死区,当车身侧偏角偏差的绝对值小于死区边界时,认为车身侧偏角已经可以接受并逐渐退出控制。死区边界设计为
(23)
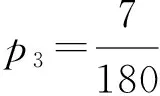
2.5 关键参数的估计
(1) 附着系数的估计
路面附着系数关系到魔术公式中轮胎力和目标车辆状态的计算,故需要进行相关估算。本文中采用双非线性度补偿的方法进行附着系数估算。首先利用侧向加速度信息确定附着系数,然后根据横摆角速度偏差和侧向速度微分确定两个车辆非线性度表征量进行附着系数的修正。具体估算方法参见文献[19]。
(2) 车身侧偏角的估计
车身侧偏角为车辆状态变量,需要进行估计作为反馈量输入控制器。本文中采用扩展的卡尔曼滤波方法进行车身侧偏角的估算,估算方法详见文献[20]。
(3) 纵向轮胎力的估算
控制器中的式(8)预测模型中用到了轮胎的纵向力,需要对其进行估计。轮胎的纵向滑移率定义为
(24)
式中:ω为车轮角速度;R为车轮半径;vx为车轮纵向速度。轮速由轮速传感器直接得到,纵向速度由车速和车辆横摆角速度计算得到。在估算得到车轮侧偏角和滑移率之后由式(2)魔术公式和式(3)计算得到车轮纵向力。
3 仿真验证
采用Carsim与Simulink联合仿真的方法对所提出的控制方法进行了仿真验证。Carsim中的车辆模型为一中级轿车,车辆参数根据实车试验参数标定得到。仿真分别针对阶跃转向试验和FMVSS126试验进行了验证。仿真中LTV-MPC控制器参数的选取如表2所示。

表2 LTV-MPC控制器参数
在本次试验中,除了本文中提出的模型预测控制器,另外采用较为常见的LQR控制器作为对比。LQR控制器的建立过程简述如下。
系统的状态方程仍为式(7)所示的形式,最优性能指标选为
(25)
式中:xd=[βref,ωref]T为控制目标,计算方法与2.4节中介绍的方法相同。
故Hamilton函数为
γT(Acx+Bcuu+Nc1e1+Nc2e2)
(26)
控制输入由下列方程求得:
u=-R-1BTγ
(27)
(28)
仿真中LQR控制器的参数取为
qx1=500;qx2=40;R=0.001×I4×4
3.1 阶跃转向试验
阶跃转向试验中,车辆首先以恒定速度80km/h直线行驶,然后输入180°转向盘阶跃转角信号。阶跃转向试验可以反映闭环控制系统的基本动态特性和系统的稳态输出特性。
LTV-MPC控制器和LQR控制器的阶跃转向试验的仿真结果如图3和图4所示。由图3(a)可见,横摆角速度在一次超调之后很快收敛到目标值附近,车身侧偏角的稳态值并不是0,而是收敛在-0.04rad附近,与车身侧偏角的目标值较为吻合。由图4(a)的控制输入曲线可见,本次试验中压力干预只在第一次超调时出现,之后由于车辆状态和目标值的误差很小,控制器没有进行控制,这也说明了上文所述的目标值的选取较为合理。可见制动力均限制在式(14)所算出的控制约束之内。从图3(b)中可以看出,LQR控制器控制的车辆横摆角速度与目标值误差较小,但车身侧偏角的误差较大。从图4(b)中可以看出,虽然控制力均在约束范围内,但LQR控制器对右侧车轮持续施加了较大的制动力。持续的制动对于车身纵向速度的影响也是驾驶员所不希望的。
3.2 FMVSS126试验
FMVSS126法规为美国交通安全部在2007年颁布的ESC性能标准测试方法。该法规要求车辆在80km/h的初始速度下进行正弦转向迟滞试验,并对横摆角速度和侧向位移做了相关要求[21]。本试验车的A值为27.9°。仿真结果如图5和图6所示。
按照FMVSS126试验法规的客观评价标准本次试验结果如表3所示,两种控制器的试验结果均达到了法规要求。
图5(a)所示车辆的横摆角速度和车身侧偏角较好地跟踪了目标值。由图5(b)可见,LQR控制器控制的车辆虽然也保证了车辆的稳定性,但是横摆角速度有较大波动,车身侧偏角的偏差也较大。对比图6中的控制输入可以看到,LTV-MPC控制器的控制输入较为平缓,避免了长时间持续制动,而LQR控制器的控制输入为长时间持续制动,这也导致了LQR控制的车辆侧向位移较小,转向跟随能力不如LTV-MPC控制的车辆好。

图3 LTV-MPC和LQR控制器阶跃转向试验

图4 LTV-MPC和LQR控制器阶跃转向试验控制输入与控制约束

图5 LTV-MPC和LQR控制器6A幅值转角FMVSS126试验
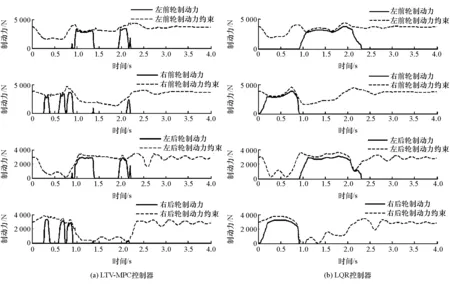
图6 LTV-MPC和LQR控制器6A幅值转角FMVSS126试验控制输入与控制约束

标准法规要求LTV-MPCLQRωz(t=2.93)/ωzmax<0.350.00483.48×10-4ωz(t=3.68)/ωzmax<0.25.88×10-40.0019Y(t=1.07)/m>1.832.532.076
在模型预测控制器的设计中,权重系数的选取对控制效果的影响很大,不合适的权重系数甚至可能导致系统丧失稳定性。本文中在以上的FMVSS126试验中分别选取不同的权重系数,对比仿真结果,说明权重系数对于控制器效果的影响。在对比中,除了上文控制器选取的gy1=500,gy2=40外,还选取了gy1=500,gy2=4和gy1=500,gy2=400两组权重系数进行对比,试验结果如图7所示。

图7 不同权重系数FMVSS126试验结果对比
由图可见:当横摆角速度偏差的权重系数从40增加到400,车身侧偏角的幅值有所增加,但对横摆角速度偏差的控制效果变化较小;当横摆角速度偏差的权重从40变为4后,控制器对车身侧偏角偏差的控制远强于对横摆角速度偏差的控制。由于横摆角速度偏差先于车身侧偏角偏差出现,而控制器对于横摆角速度偏差不够敏感,导致开始阶段控制严重不足。当车身侧偏角偏差快速增大后车辆已经发生侧滑,制动控制已经不能使车辆保持稳定。对比发现取gy1≈10gy2比较合理。
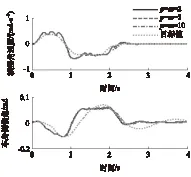
图8 不同预测时域126试验车身侧偏角对比
根据模型预测控制的原理,控制器仅在预测时域范围内求解最优解,并将最优解的第一个分量作用于系统,故理论上得到的是一个局部最优解。根据预测时域的大小不同,求解最优解的范围也不同。为了分析预测时域对于控制器的影响,进行了不同预测时域控制器的对比试验。试验中,分别取p=m=2,p=m=5,p=m=10,即预测时域等于控制时域,且分别为2,5和10个周期,试验条件同上述的6A幅值转角的FMVSS126试验,结果如图8所示。可以看出,提高预测时域和控制时域虽然能在一定程度上改善控制效果,但3组曲线的区别很小。这主要是因为在ESC控制中控制周期较短,预测时域和控制时域的变化对于控制器的求解影响不很明显。在系统周期较长的过程控制问题中预测时域的作用才会比较明显地体现出来。预测时域和控制时域的增加会明显增加计算量,降低控制器运行效率。以上3组仿真试验的运行时间分别为3.21,6.39和47.11s,故从运行效率和控制效果两方面综合来看,采用2周期预测2周期控制的控制器是一个较好的选择。
4 结论
本文中将线性时变参数模型预测控制运用于ESC主动制动控制中,建立了基于差动制动的LTV-MPC ESC控制器,文中详细推导了该控制器的设计和求解过程。该控制器既考虑到车辆模型的非线性特性,又尽可能降低了控制器的运算量,通过对轮胎模型进行局部线性化的方法将非线性车辆运动问题转化为线性模型预测控制问题,保留了模型预测控制适于处理包含约束的多变量优化问题的优点。
通过仿真试验,对比了该控制器和传统的LQR控制器的控制效果,验证了该控制器的可行性,该控制器在阶跃转向试验和FMVSS126法规试验中都得到了较好的控制效果。通过对比分析对控制器的参数进行了优化。
目前该控制方法距离实车试验还有一定的距离,下一步的工作是对控制器的求解过程进行进一步的优化,降低控制器计算量,以达到目前车用MCU对于计算量的要求。另外需要研究观测量误差对于控制器的影响。
[1] MANNING W J, CROLLA D A. A Review of Yaw Rate and Sideslip Controllers for Passenger Vehicles[J]. Transactions of the Institute of Measurement and Control,2007,29(2):117-135.
[2] ABE M, KANO Y, SUZUKI K, et al. Side-slip Control to Stabilize Vehicle Lateral Motion by Direct Yaw Moment[J]. JSAE Review,2001,22(4):413-419.
[3] 王德平,郭孔辉,宗长富.车辆动力学稳定性控制的理论研究[J].汽车工程,2000,32(1).
[4] ESMAILZADEH E, GOODARZI A, VOSSOUGHI G R. Optimal Yaw Moment Control Law for Improved Vehicle Handling[J]. Mechatronics,2003,13(7):659-675.
[5] PARK K, HEO S J, BAEK I. Controller Design for Improving Lateral Vehicle Dynamic Stability[J]. JSAE Review,2001,22(4):481-486.
[6] GHIKE C, SHIM T, ASGARI J. Integrated Control of Wheel Drive-Brake Torque for Vehicle-handling Enhancement[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering,2009,223(4):439-457.
[7] CHUNG T, Yi K. Design and Evaluation of Side Slip Angle-based Vehicle Stability Control Scheme on a Virtual Test Track[J]. Control Systems Technology, IEEE Transactions on,2006,14(2):224-234.
[8] FALCONE P, BORRELLI F, ASGARI J, et al. Predictive Active Steering Control for Autonomous Vehicle Systems[J]. Control Systems Technology, IEEE Transactions on,2007,15(3):566-580.
[9] CHANG S, GORDON T J. A Flexible Hierarchical Model-based Control Methodology for Vehicle Active Safety Systems[J]. Vehicle System Dynamics,2008,46(S1):63-75.
[10] KATRINIOK A, ABEL D. LTV-MPC Approach for Lateral Vehicle Guidance by Front Steering at the Limits of Vehicle Dynamics[C]. Decision and Control and European Control Conference (CDC-ECC),2011 50th IEEE Conference on. IEEE,2011:6828-6833.
[11] BARBARISI O, PALMIERI G, SCALA S, et al. LTV-MPC for Yaw Rate Control and Side Slip Control with Dynamically Constrained Differential Braking[J]. European Journal of Control,2009,15(3):468-479.
[12] RE Luigi Del, GLIELMO Luigi, GUARDIOLA Carlos. Automotive Model Predictive Control: Models, Methods and Applications[M]. London: Springer,2010.
[13] PACEJKA H. Tire and Vehicle Dynamics[M]. Amsterdam: Elsevier,2005.
[14] ABE M. Vehicle Dynamics and Control for Improving Handling and Active Safety: from Four-wheel Steering to Direct Yaw Moment Control[J]. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics,1999,213(2):87-101.
[15] VAN Zanten A T, ERHARDT R, PFAFF G, et al. Control Aspects of the Bosch-VDC[C]. AVEC.1996,96:573-608.
[16] RAJAMANI R. Vehicle Dynamics and Control[M]. Springer,2011.
[17] ZHENG S, TANG H, HAN Z, et al. Controller Design for Vehicle Stability Enhancement[J]. Control Engineering Practice,2006,14(12):1413-1421.
[18] MOKHIAMAR O, ABE M. Simultaneous Optimal Distribution of Lateral and Longitudinal Tire Forces for the Model Following Control[J]. Journal of Dynamic Systems, Measurement, and Control,2004,126(4):753-763.
[19] 李亮,朱宏军,陈杰,等.用于汽车稳定性控制的路面附着识别算法[J].机械工程学报,2014,50(2):132-138.
[20] LI L, JIA G, RAN X, et al. A Variable Structure Extended Kalman Filter for Vehicle Sideslip Angle Estimation on a Low Friction Road[J]. Vehicle System Dynamics,2014,52(2):280-308.
[21] NHTSA-200727662. Federal Motor Vehicle Safety Standards; Electronic Stability Control Systems; Controls and Displays[S]. USA. Department of Transportation National Highway Traffic Safety Administration,2007.
A Study on Vehicle Stability Control Based on LTV-MPC
Chen Jie, Li Liang & Song Jian
TsinghuaUniversity,StateKeyLaboratoryofAutomotiveSafetyandEnergy,Beijing100084
In view of the problem of the stability control of vehicle with the constraints of adhesive force and hydraulic actuators, a linear time-varying model predictive control (LTV-MPC) method based on nonlinear vehicle model is proposed in this paper. In the method, the nonlinear vehicle model is locally linearized, and with the braking force input limit obtained by realtime parameter estimation, the MPC problem is transformed into a quadralic programming problem to get the optimal solutions, with the issue of active braking pressure distribution with constraints resolved. In addition, the selection of control objective in MPC controller is discussed, and the effects of control parameter selection on control results and operation efficiency are analyzed. The results of both steady and trasient simulations verify the feasibility and effectiveness of MPC controller.
vehicle dynamics; model predictive control; stability control
*国家自然科学基金(51275557)和国家自然科学基金优秀青年基金(51422505)资助。
原稿收到日期为2014年10月11日,修改稿收到日期为2014年12月28日。

