基于区间多阶段随机规划模型的灌区多水源优化配置

付　强，刘银凤，刘　东，李天霄，刘　巍，Amgad Osman（东北农业大学水利与建筑学院，哈尔滨150030）



基于区间多阶段随机规划模型的灌区多水源优化配置

付强，刘银凤，刘东，李天霄，刘巍，Amgad Osman
（东北农业大学水利与建筑学院，哈尔滨150030）

摘要：灌区多水源灌溉系统中存在许多不确定性因素，随着系统环境的变化及不确定性因素的影响，导致其配水过程具有动态特征。针对灌区多水源灌溉系统的配水特点，该文建立基于区间多阶段随机规划的灌区多水源优化配置模型。同时，考虑灌溉水对作物产量的影响，引入水分敏感指数权重系数，并以黑龙江省和平灌区水稻不同生育阶段灌溉水资源优化配置进行实例研究。结果表明，在不同来水情境下，管理者可根据各个生育阶段水分敏感指数权重系数，判断作物不同生育阶段的需水敏感程度，当来水情境的来水量多时，会产生余水量，可调配给下一生育阶段；当来水情境的来水量少时，管理者可在减少灌溉水量与增加外调水之间进行权衡，并根据需水关键期与需水非关键期做出决策，使水资源在作物生育阶段间及作物生育阶段内进行分配，实现灌区多水源灌溉系统的动态配水。该模型的应用在确保作物产量的同时，使灌溉水资源在作物各个生育阶段进行合理配置，有效地避免了水资源浪费，对提高灌溉水利用效率、保证水资源的可持续利用具有重要意义。

关键词：模型；灌溉；作物；灌区多水源；不确定性；区间多阶段随机规划模型；优化配置

付强，刘银凤，刘东，李天霄，刘巍，Amgad Osman.基于区间多阶段随机规划模型的灌区多水源优化配置[J].农业工程学报，2016，32（01）：132-139.doi：10.11975/j.issn.1002-6819.2016.01.018 http://www.tcsae.org

Fu Qiang, Liu Yinfeng, Liu Dong, Li Tianxiao, Liu Wei, Amgad Osman.Optimal allocation of multi-water resources in irrigation area based on interval-parameter multi-stage stochastic programming model[J].Transactions of the Chinese Society of Agricultural Engineering（Transactions of the CSAE）, 2016, 32（01）: 132－139.（in Chinese with English abstract）doi：10.11975/j.issn.1002-6819.2016.01.018 http://www.tcsae.org

中国农业工程学会会员：付强（E041100051S）

0　引言

作为人类活动的重要资源之一，水资源对保障社会、经济、环境、生态的可持续发展起着决定性作用。随着各种各样的水资源问题的浮现，导致水的供需矛盾日益恶化，如何协调好水资源的供需关系，确保水资源合理高效的利用，是水资源领域研究的热点问题。农业是用水大户，农业水资源“瓶颈”制约问题愈加凸显，提高农业用水效率对解决水资源供需矛盾、缓解用水压力具有十分重要的意义。灌区作为农业用水主体，对灌区农业灌溉水资源进行合理配置，势必是提高农业用水效率、可持续开发和利用水资源的有效途径[1]。

近年来，灌区水资源优化配置的研究不断涌现[2-5]，灌区灌溉系统受气候变化[6]、水管理政策以及作物生长特性等诸多因素的影响，具有时空效应，是一个复杂的动态配水过程，传统的确定性方法往往疏于考虑这方面问题，在处理灌区灌溉系统中不确定性因素间的复杂性关系时，存在一定的局限性，而基于不确定性条件下的区间二阶段随机规划模型，作为解决复合系统中不确定性的有效方法，在水资源领域得到了广泛的应用[7-10]，该方法虽然解决了水资源系统中的经济、资源等因素的不确定性，却不能反映系统环境的动态变化，而区间多阶段随机规划模型，不仅可以解决系统不确定性，同时能够反映多情境下的系统动态变化过程，该模型在水资源管理中已取得了一定的成果，Li和Huang将多阶段随机二次规划方法应用于水资源管理中[11]。Li等将多阶段随机规划与整数规划相结合，处理水库系统中存在的不确定性问题[12]。Dai等将多阶段灌溉水资源配置模型应用到农业水资源管理与耕地利用模式优化中[13]。莫淑红等建立基于场景的多阶段随机规划模型，对陕西省宝鸡市冯家山水库多用户供水方案决策问题进行研究[14]。本文在上述学者研究的基础上，对区间多阶段随机规划模型进行了改进，考虑灌区内作物各生育阶段的敏感指数，在模型中引入水分敏感指数权重系数，采用区间多阶段随机规划模型在作物各生育阶段间进行优化配水，使其适用于灌区内多水源作物不同生育阶段间优化配置。模型中同时引入概率密度函数和离散区间处理不确定性参数，其中，概率密度函数可表示水文随机变量的不确定性，离散区间表示其他水文及经济参数的不确定性，多阶段随机规划则可在一系列来水情境下，对各个生育阶段内部与阶段之间进行水量调配，从而实现灌区多水源作物不同生育阶段的实时动态配水。

1　灌区多水源区间多阶段随机规划模型

1.1模型建立

在灌区农业灌溉系统中，影响作物产量的因素有很多，本文仅考虑灌溉水对作物产量的影响，不同供水工程灌溉供水情况均要受来水量的影响，具有较强的随机性。因此，作物各生育阶段不同供水工程的供水量是随机变量，具有不确定性特点，这就要求各相关供水工程的供水决策必须在各阶段该随机变量不同离散概率水平下及时的做出，该过程具有动态特性，针对这样的问题，可以运用多阶段随机规划模型来解决。该模型可反映水资源管理中系统的无可预计性，即对未来阶段随机变量的实现不可预计时，必须对当前每一阶段做出决策[15]。

在分析灌区水资源承载力和作物生长特征的基础上，要求管理者对当年灌溉水量预先做出决策，为作物各个生育阶段设定一个初始的供水目标值，由于不同供水工程在各个阶段内的来水情况的随机性特点，一旦供水量没有达到初始供水目标值，那就需要通过减少灌溉水量或者外调水源进行补水，而减少灌溉水量会影响作物产量，外调水源补水会产生附加费用，都会产生相应的经济惩罚，因此，为使灌区灌溉净效益最大化，本文根据作物不同生育阶段缺水对最终产量的影响有较大差异（即需水敏感性不同）的特点，引入水分敏感指数权重系数，用来权衡不同生育阶段的需水程度，判断各个生育阶段是否处于需水关键期（作物需水关键期是指缺水时对作物的产出影响大的时期），从而在减少灌溉用水与外调水源补水之间进行选择，使经济惩罚降到最低。

本文运用Jensen模型，计算各个生育阶段的水分敏感指数[16-18]，并得到作物不同生育阶段的水分敏感指数权重系数。

Jensen模型表述如下：

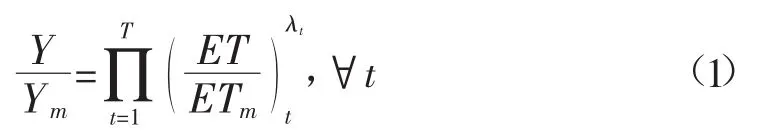
式中t为作物生育阶段；T为作物生育阶段总数；λt为第t阶段作物产量对缺水的敏感指数；ET为作物的实际腾发量，mm；ETm为作物的潜在腾发量，mm；Y为实际腾发量对应的作物实际产量，kg/hm2；Ym为潜在腾发量对应的作物潜在产量，kg/hm2。

对Jensen模型做如下变换：

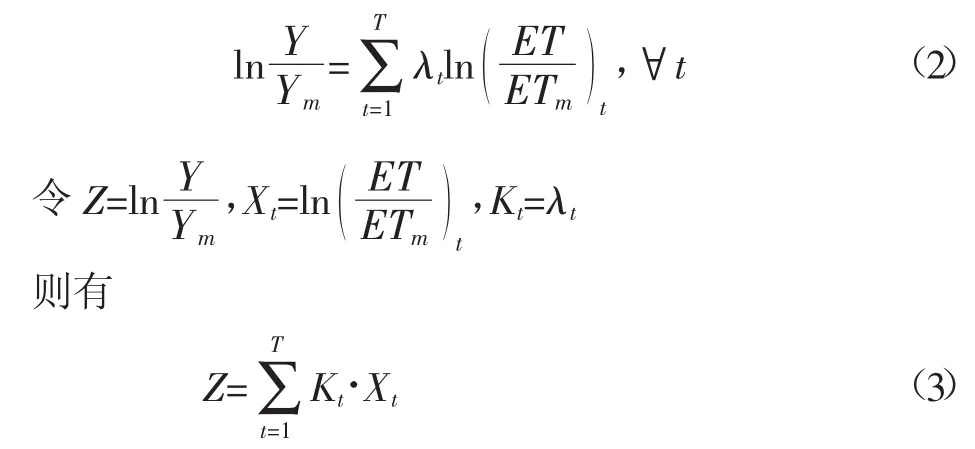
试验总处理m个，处理j=1，2，…，m，得到m组Xtj、Zj，采取最小二乘法，以使估计值与观测值间的误差平方和最小：

求得Kt值后，由Kt=λt即可求得λt。

利用Jensen模型计算得到λt值，进而计算作物不同生育阶段的水分敏感指数权重系数：

水分敏感指数权重系数越大，表示缺水对产量影响越大，属于需水关键期；水分敏感指数权重系数越小，表示缺水对产量影响越小，属于需水非关键期。将水分敏感指数权重系数引入多阶段随机规划模型中，假定各阶段需水量已确定时，建立灌区多水源多阶段随机规划模型：

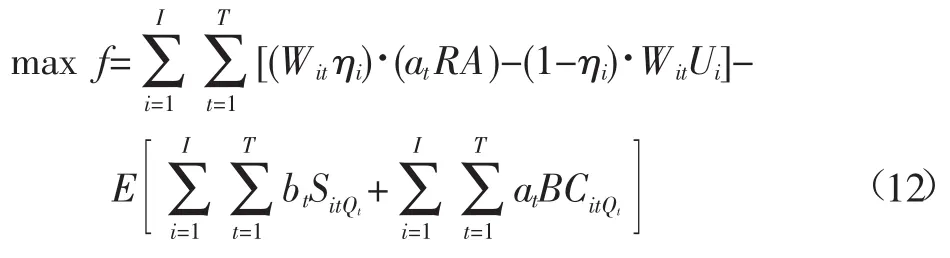
约束条件：

1）供水约束

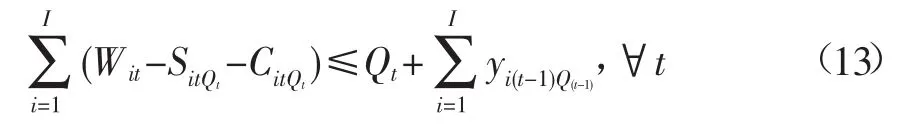
2）余水约束

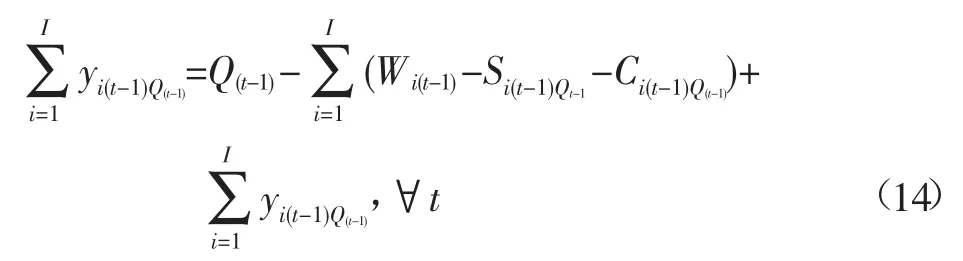
3）配水量约束

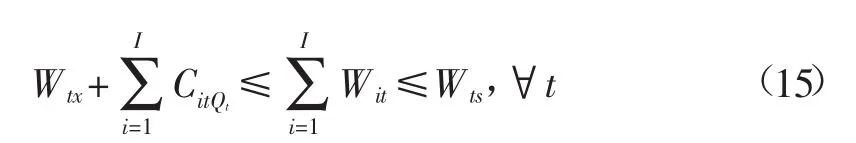
4）非负约束

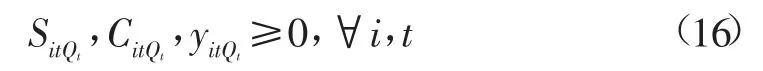
式中f为灌溉净效益，元；i为供水工程，其中i=1，2，3分别代表引水工程、提水工程、井灌工程；为配水周期即作物生育阶段，与式（1）相同；Wit为i供水工程t配水周期的供水目标，m3；ηi为i供水工程渠系水利用系数；ai为t配水周期水分敏感指数权重系数；R为灌溉水分生产率，kg/ m3；A为作物市场单价，元/kg；Ui为i供水工程供水成本，元/m3；bt为t配水周期外调水成本，元/m3；B为缺水惩罚，元/m3；Qt为t配水周期可用来水总量，是随机变量，m3；SitQt为可用水量为Qt时，供水量未达到初始目标Wit的外调水量，m3；CitQt为可用水量为Qt时，供水量未达到初始目标Wit的缺水量，m3；E（t）为随机变量的期望值；yitQt为i供水工程t配水周期的剩余水量，m3；Wtx为灌溉需水量下限值，m3；Wts为灌溉需水量上限值，m3。

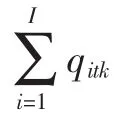
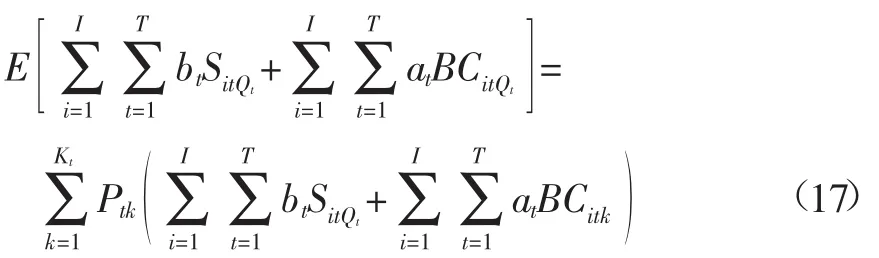
除考虑可用水量Qt的不确定性外，作物的初始供水目标（Wit），作物市场价格（A），产量的高低（R），调、配水成本（bt、Ui），以及缺水惩罚系数（B），都是不确定的，因此为了表述这些参数的不确定性，将区间参数引入模型中，区间参数的上、下限值分别对应着不确定性变量的上、下限值，这样灌区多水源区间多阶段随机规划模型可变为:

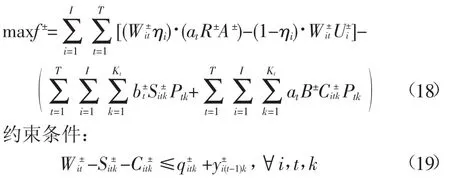
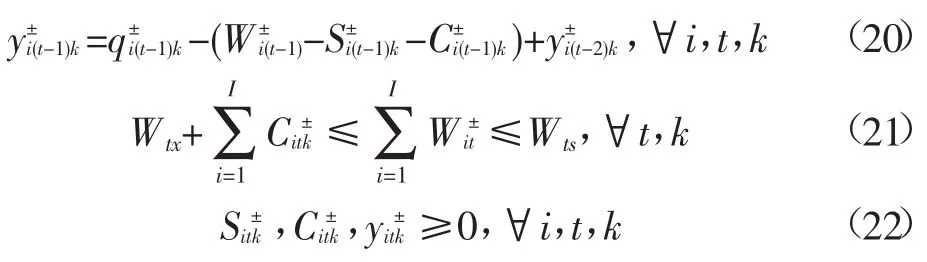
1.2模型求解

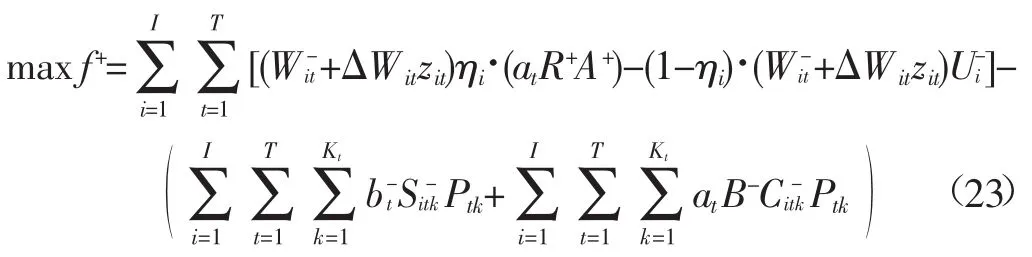
约束条件：

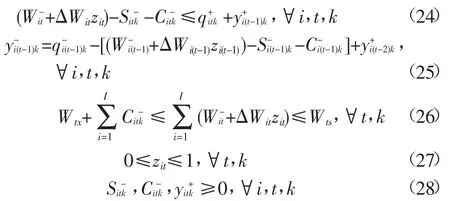
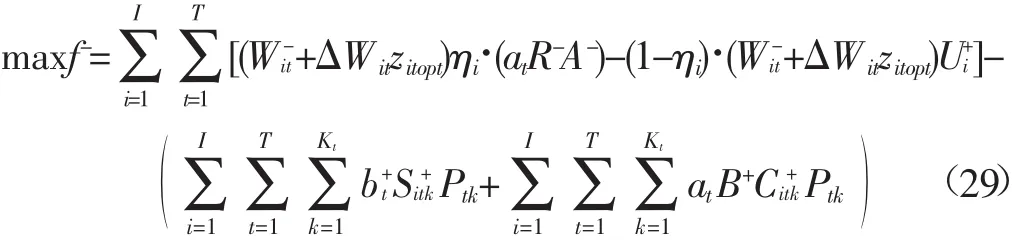
约束条件：

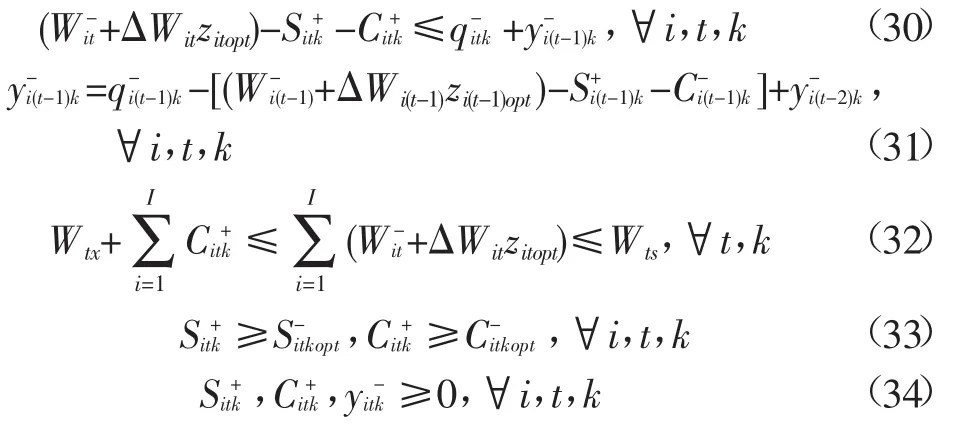
模型优化结果：

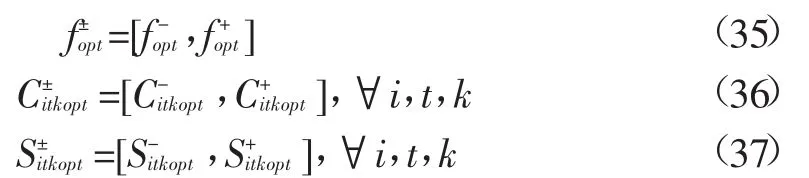
最优配水量：

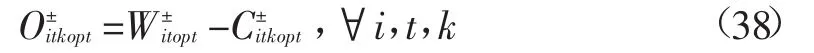
2　案例研究

2.1灌区概况

和平灌区位于黑龙江省绥化市庆安县中部，呼兰河左岸的干支流河漫滩及一级阶地上，灌区范围由东向西呈带状分布。该灌区主要水源有地表水与地下水，取水方式又可分为3个供水工程，即引水工程、提水工程和井灌工程，井灌工程由地下水提供，其他两个供水工程由地表水提供，同时有柳河水库作为外调水源。

2.2参数确定

和平灌区是黑龙江省水稻灌溉试验基地，以水稻作为主要的生产作物，因此，本文选取水稻作为典型作物，进行配水研究。由于返青期稻苗较小、黄熟期自然落干，水稻的腾发量都较小，本文只选取分蘖期、拔节期、抽穗期、乳熟期4个生育阶段进行水分敏感指数及配水计算[20]，因此，作物生育阶段取t＝1，2，3，4分别代表分蘖期、拔节期、抽穗期、乳熟期。Jensen模型的输入数据来源于国家科技支撑计划项目（2012BAD08B05）采用公式（1）和（11）计算作物水分敏感指数及水分敏感指数权重系数，见表1；根据《呼兰河灌区工程初期设计报告》以及当地水务局提供的调研数据，对水稻不同生育阶段需水量以及各个供水工程灌溉控制面积分析，得到各供水工程的初始供水目标以及水稻充分灌溉条件下的需水上、下限值，见表2；综合分析灌区内多年降雨和径流统计资料，假设不同生育阶段来水水平的可能情况为高、中、低3种，其中，高来水水平和低来水水平出现的概率大致相同，中来水水平的概率高于其他2种来水水平，因此，假设不同生育阶段3种来水水平出现的概率分别为0.2、0.6、0.2。由上述资料可获得不同生育阶段各供水工程在不同概率水平下的可用水量区间值，见表3。

表1　水分敏感指数及水分敏感指数权重系数Table 1 Water sensitive index and Water sensitive index weight coefficient

表2　不同生育阶段各供水工程的初始配水目标Table 2　 Initial water supply targets for water supply projects in different growth stages

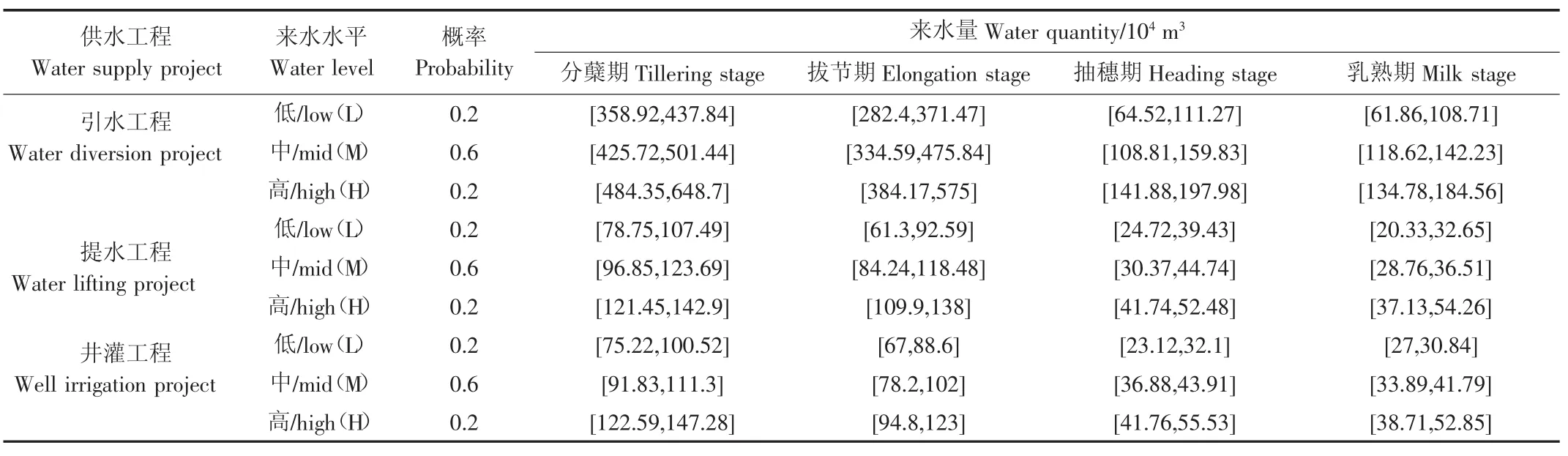
表3　不同生育阶段各供水工程的可用水量Table 3 Available water of water supply projects in different growth stages

不同供水工程的其他相关参数，见表4。本文中相关经济参数作物价格、外调水成本、缺水惩罚、水分生产率的取值区间分别为：[3.4，3.56]、[1.8，2]、[7.2，8]、[3，3.2]，其中取外调水成本在各生育阶段都相等。

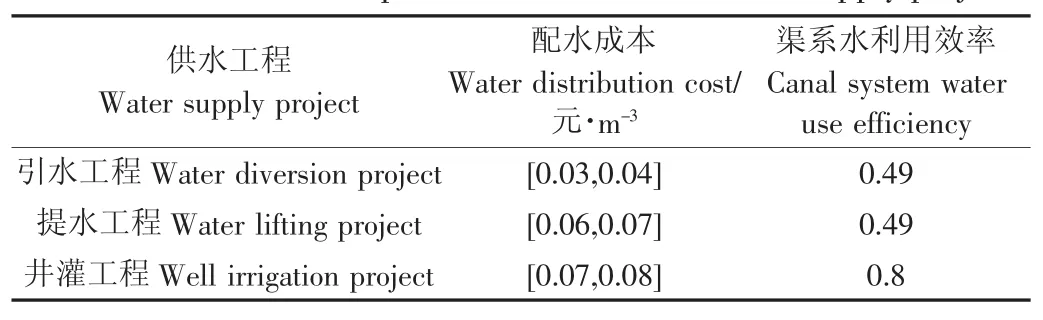
表4　不同供水工程其他相关参数Table 4 Other relevant parameters of different water supply projects

2.3情境分析

在此，可根据随机变量Qt的可能概率构建分支结构为1-3-3-3-3的四情境树，每个供水工程可产生一个周期为4（5阶）的情境树，且各情境树具有相同的结构。由起始时刻0开始，第1周期分出3个节点；第2周期，在第1周期的基础上，每个节点继续分出3个节点，以此类推，第2周期为9个节点，3、4周期分别为27个节点和81个节点。本文有3个供水工程，因此，第1周期就会产生9个节点，形成3-9-27-81-243的情境树，如图1所示，由于运行结果数据量过大，本文在每个生育阶段各供水工程，只选取3种典型来水情境进行分析[13]，分蘖期（t=1），选取（L，M，H）作为典型来水情境，分别表示低、中、高来水情境；拔节期（t=2），选取（L-L，M-M，H-H）作为典型来水情境，分别表示t=1、2时均处于低、中、高来水情境；抽穗期（t=3）选取（L-L-L，M-M-M，H-H-H）作为典型来水情境，分别表示t=1、2、3时均处于低、中、高来水情境；乳熟期（t=4）选取（L-L-L-L，M-M-M-M，H-H-H-H）作为典型来水情境，分别表示t=1、2、3、4时均处于低、中、高来水情境。

3　模型结果与分析

运用Matlab和Lingo11编程求解灌区多水源区间多阶段随机规划模型。由模型运行结果可得：

在t=1和t=2时，决策变量zitopt分别为z11opt=1，z21opt=1，z31opt=1和z12opt=1，z22opt=1，z32opt=1，均使最优供水目标W±itopt达到初始配水目标W±it的上限值，分别为：W11opt=629.97万m3，W21opt=156.46万m3，W31opt=139.44万m3和W12opt=546.48 万m3，W22opt=135.72万m3，W32opt=120.96万m3；

在t=3和t=4时，z13opt=0.5，z23opt=0.2，z33opt=1和z14opt=0，z24opt=0，z34opt=1，则存在最优供水目标未达到初始配水目标W±it上限值的情况，且z14opt=0和z24opt=0时，最优供水目标取W±it的下限值，其最优供水目标分别为：W13opt=159.82 万m3，W23opt=44.75万m3，W33opt=52.84万m3和W14opt=189.75 万m3，W24opt=47.13万m3，W34opt=57.12万m3。

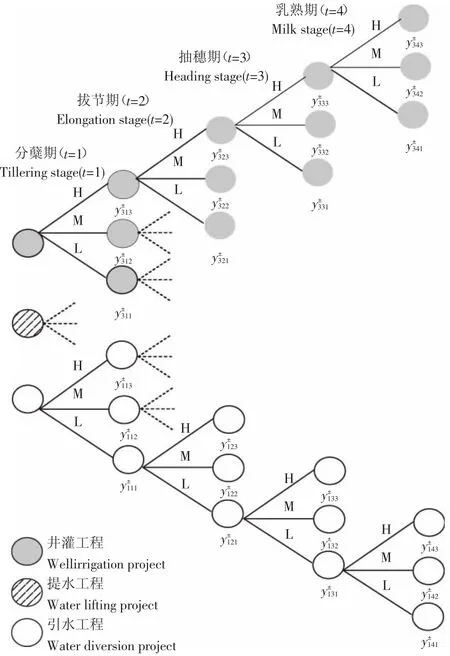
图1　灌区多水源作物生育期配水多阶段情境树Fig.1 Multi-stage scenario tree of water distribution in the growing stage of multiple water resources in irrigation district

上述模型优化结果表明：在作物需水关键期时（t=1 和t=2），为达到高产的目的，模型选择了充分满足作物需水，在需水非关键期时（t=3和t=4），为了提高灌溉水利用效率，节约水资源以及降低供水成本，模型则选择了减少作物供水量。在来水量不确定的情况下，满足高用水需求的风险大，用水量得不到满足时的惩罚也大，而满足低用水需求的风险小，惩罚也小，但低用水需求时产生的经济效益会更少，说明供水量、风险与经济效益三者紧密相连。

最优配水量是由最优供水目标与缺水量之间的差值确定的，可由公式求得，分蘖期（t=1）和拔节期（t=2），处于需水关键期，管理者希望充分满足作物的用水需求，保证产量，因此，在这2个生育阶段内，模型选择不缺水，缺水量值均为0，即在不同典型来水情境下，当灌区内来水量不能满足供水需求时，各个供水工程会根据模型的选择存在不同程度的外调水量，以满足各生育阶段内配水目标；而抽穗期（t=3）和乳熟期（t=4），属于需水非关键期，缺水对作物产量的影响很小，因此，为了降低供水成本，节约资源，模型做出了缺水的选择，对于同一供水工程而言，随着来水量的增加，灌区内供水量会不断增加，缺水量会逐渐减小，最优配水量则逐渐增大。

外调水量的大小取决于灌区内水源能满足最优配水量的程度。结合模型运行结果，绘制不同配水周期，不同典型供水情境下，各个供水工程最优配水量、外调水量以及灌区供水量的变化情况，如图2所示。由图2a、2b知，在分蘖期（t=1），对同一个供水工程而言，不同来水情境下，最优配水量相同，随着来水水平的增加，外调水量呈现出递减的趋势，而灌区供水量则呈现逐渐递增的趋势。由图2c、2d知，在拔节期（t=2），3种典型来水情境下，灌区供水量取下限值时，各供水工程都有外调水量，且随供水量的增加而减小；灌区供水量取上限值时，在高来水情境（HH）下，外调水量为0，最优配水量均由灌区提供。由图2e、2f知，在抽穗期（t=3），只有灌区供水量为下限值时，引水工程与井灌工程的低来水情境（L-L-L）有少量的外调水。由图2g、2h知，在乳熟期（t=4），不同来水情境时的来水量略低于抽穗期（t=3），因此，灌区供水量下限值，除高水平情境（H-H-H-H）外，其他来水情境均有外调水量，而灌区供水量为上限值时，只有引水工程低来水情境（L-L-L-L）时，有外调水量。可见，对于作物需水非关键期（t=3和t=4），模型选择了减少灌溉水量，但各供水工程仍然存在外调水，这是因为即使管理者选择了缺水的情况，也要满足作物的最低需水量，确保作物的基本生理需求，因此，在模型选择缺水的情况下，仍存在一定量的外调水补给。

结合图2h和表3，该模型不仅可在同一生育阶段内进行水量调配，还能在4个生育阶段间水量调配。由于来水量年内分布不均，在来水量高，配水目标小时，会有一定的余水量，这时可以将余水量拦蓄起来，供给下一阶段来水量小的生育阶段，例如乳熟期（t=4），在高来水情境（HH-H-H）时，引水工程和井灌工程没有外调水量，但最优配水量的上限值分别为189.75万m3和57.12万m3，均大于该来水情境的最大来水量184.56万m3和52.85万m3，原因就是，抽穗期（t=3）存在余水量，并将余水量调配给乳熟期（t=4），这样不仅减小了引水工程和井灌工程在该来水情境下缺水的经济惩罚，同时有效的解决了水资源时间上分布不均的问题，避免了由于来水大于需水造成的水资源浪费，实现水资源时间与空间上的实时动态配置。

模型求解得到的最终灌区灌溉效益值为：fopt=[2 568.88, 4 033.34]万元。由于不同的配水形式以及系统的不确定性，使最终的灌溉效益以区间值给出，以适应不同配水决策，灌区最终收益会在该区间内取得。

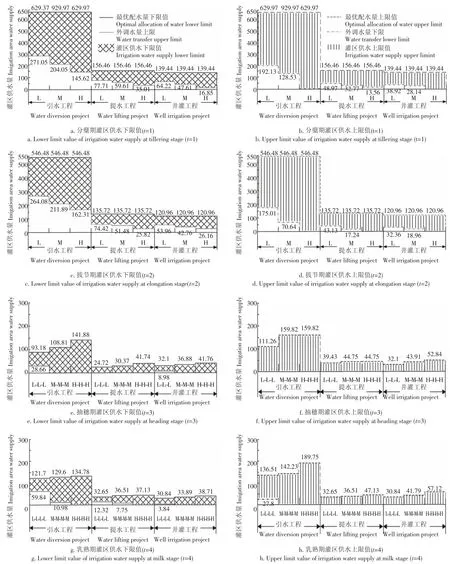
图2　不同生育阶段不同来水情境下各供水工程的灌区供水量Fig.2 Irrigation water supply at different growth stages in different water conditions of water supply project/104m3

4　结论

1）本文针对作物不同生育阶段需水敏感程度的差异，将水分敏感指数权重系数引入区间多阶段随机规划模型，用概率密度函数以及离散区间来表示水资源系统中存在的不确定性，多阶段随机规划表示配水过程的动态特性，建立适用于灌区多水源的区间多阶段随机规划模型，并以离散情境树的形式反映水资源配置过程，将和平灌区水稻不同生育阶段水资源配置作为实例进行研究。

2）根据水分敏感指数权重系数判断作物需水关键期与需水非关键期，模型求解结果表明，当灌区内供水不足时，在需水关键期，即分蘖期（t=1）和拔节期（t=2），选择外调水；在需水非关键期，即抽穗期（t=3）和乳熟期（t=4），选择缺水，但在来水量少时的来水情境下，为满足作物的基本生理需水，仍会存在一定量的外调水。管理者可以依据模型在外调水与缺水之间做出决策，这样在保证作物产量的同时，减少不必要的灌溉水量，不仅能够降低供水成本，还可使水资源得到合理高效的利用，提高了灌溉水利用效率。

3）通过分析各个供水工程最优配水量、外调水量以及灌区供水量之间的变化关系，得到该模型可同时在同一生育阶段内和不同生育阶段间进行水量调配，从空间与时间的角度，实现了灌区多水源不同生育阶段灌溉水优化配置的动态过程。

[参考文献]

[1]齐学斌，黄仲冬，乔冬梅，等.灌区水资源合理配置研究进展[J].水科学进展，2015，26（02）：287-295.Qi Xuebin, Huang Zhongdong, Qiao Dongmei, et al.Research advances on the reasonable water resources allocation in irrigation district [J].Advances in Water Science, 2015, 26（02）: 287-295.（in Chinese with English abstract）

[2]张展羽，高玉芳，李龙昌，等.沿海缺水灌区水资源优化调配耦合模型[J].水利学报，2006，37（10）：1246-1252+1258.Zhang Zhanyu, Gao Yufang, Li longchang, et al.Optimal utilization of water resource in coastal water-deficient irrigation region[J].Journal of Hydraulic Engineering, 2006, 37（10）: 1246-1252+1258.（in Chinese with English abstract）

[3]陈卫宾，董增川，张运凤.基于记忆梯度混合遗传算法的灌区水资源优化配置[J].农业工程学报，2008，24（6）：10-13.Chen Weibin, Dong Zengchuan, Zhang Yunfeng.Optimization the allocation of irrigated areas water resources based on memory gradient hybrid genetic algorithm[J].Transactions of the Chinese Society of Agricultural Engineering（Transactions of the CSAE）, 2008, 24（6）: 10-13.（in Chinese with English abstract）

[4]代锋刚，蔡焕杰，刘晓明，等.利用地下水模型模拟分析灌区适宜井渠灌水比例[J].农业工程学报，2012，28（15）：45-51.Dai Fenggang, Cai Huanjie, Liu Xiaoming, et al.Analysis of suitable irrigation water ratio of well to channel based on groundwater model [J].Transactions of the Chinese Society of Agricultural Engineering（Transactions of the CSAE）, 2012, 28 （15）: 45-51.（in Chinese with English abstract）

[5]陈述，邵东国，李浩鑫，等.基于粒子群人工蜂群算法的灌区渠-塘-田优化调配耦合模型[J].农业工程学报，2014，30 （20）：90-97.Chen Shu, Shao Dongguo, Li Haoxin, et al.Coupled allocation model for optimizing water in canal-pond-field based on artificial bee colony and particle swarm algorithm [J].Transactions of the Chinese Society of Agricultural Engineering（Transactions of the CSAE）, 2014, 30（20）: 90-97.（in Chinese with English abstract）

[6] Parsinejad M, Yazdi A B, Araghinejad S, et al.Optimal water allocation in irrigation networks based on real time climatic data [J].Agricultural Water Management, 2013, 117: 1-8.

[7] Maqsood I, Huang G H, Huang Y F, et al.ITOM: an intervalparameter two-stage optimization model for stochastic planning of water resources systems[J].Stochastic Environmental Research and Risk Assess, 2005, 19（2）: 125-133.

[8] Lu H W, Huang G H, Li H.Inexact rough-interval two-stage stochastic programming for conjunctive water allocation problems[J].Journal of Environmental Management, 2009, 91（1）: 261-269.

[9]张静，黄国和，刘烨，等.不确定条件下的多水源联合供水调度模型[J].水利学报，2009，40（2）：160-165.Zhang Jing, Huang Guohe, Liu Ye, et al.Dispatch model for combined water supply of multiple sources under the conditions of uncertainty[J].Journal of Hydraulic Engineering, 2009, 40（2）: 160-165.（in Chinese with English abstract）

[10]付银环，郭萍，方世奇，等.基于两阶段随机规划方法的灌区水资源优化配置[J].农业工程学报，2014，30（5）：73-81.Fu Yinhuan, Guo Ping, Fang Shiqi, et al.Optimal water resources planning based on interval-parameter two-stage stochastic programming[J].Transactions of the Chinese Society of Agricultural Engineering（Transactions of the CSAE）, 2014, 30（5）: 73-81.（in Chinese with English abstract）

[11] Li Y P, Huang G H.Inexact multistage stochastic quadratic programming method for planning water resources systems under uncertainty [J].Environmental Engineering Science, 2007, 24 （10）: 1361-1377.

[12] Li Y P, Huang G H, Nie S L, et al.Inexact multistage stochastic integer programming for water resources management under uncertainty[J].Journal of Environmental Management, 2008, 88 （1）: 93-107.

[13] Dai Z Y, Li Y P.A multistage irrigation water allocation model for agricultural land-use planning under uncertainty [J].Agricultural Water Management, 2013, 129: 69-79.

[14]莫淑红，段海妮，沈冰，等.考虑不确定性的区间多阶段随机规划模型研究[J].水利学报，2014，45（12）：1427-1434.Mo Shuhong, Duan Haini, Shen Bing, et al.Study on an interval multi-stage stochastic programming approach[J].Journal of Hydraulic Engineering, 2014, 45（12）: 1427-1434.（in Chinese with English abstract）

[15] Li Y P, Huang G H, Nie S L.An interval-parameter multi-stage stochastic programming model for water resources management under uncertainty [J].Advances in Water Resources, 2006, 29 （5）: 776-789.

[16]崔远来，茆智，李远华.水稻水分生产函数时空变异规律研究[J].水科学进展，2002，13（4）：484-491.Cui Yuanlai, Mao Zhi, Li Yuanhua.Study on temporal and spatial variation of rice water production function[J].Advances in Water Science, 2002, 13（4）: 484-491.（in Chinese with English abstract）

[17]王克全，付强，季飞，等.查哈阳灌区水稻水分生产函数模型及其应用试验研究[J].灌溉排水学报，2008，27（3）：109-111.Wang Kequan, Fu Qiang, Ji Fei, et al.Water production function of rice and its application in Cha ha yang Irrigation area [J].Journal of Irrigation and Drainage, 2008, 27（3）: 109-111.（in Chinese with English abstract）

[18]程卫国，卢文喜，安永凯.吉林省水稻水分生产函数模型的适应性研究[J].灌溉排水学报，2015，34（2）：61-66.Cheng Weiguo, Lu Wenxi, An Yongkai.Adaptability of water production function model for rice Jilin Province [J].Journal of Irrigation and Drainage, 2015, 34（2）: 61-66.（in Chinese with English abstract）

[19] Huang G H, Baetz B W, Patry G G.Capacity planning for municipal solid waste management systems under uncertainty—a grey fuzzy dynamic programming（GFDP）approach[J].J Urban Plan, 1994, 120: 132-156.

[20]峁智，崔远来，李远华.水稻水分生产函数及其时空变异理论与应用[M].北京：科学出版社，2003.

Optimal allocation of multi-water resources in irrigation area based on interval-parameter multi-stage stochastic programming model

Fu Qiang, Liu Yinfeng, Liu Dong, Li Tianxiao, Liu Wei, Amgad Osman
（College of Water Conservancy and Architecture, Northeast Agricultural University, Harbin 150030, China）

Abstract:There are many uncertain factors in the multi-source water irrigation system, along with the changes in the system environment and the effects of uncertainty, leading to dynamic characteristics of the water distribution process.Based on the water distribution characteristics of irrigation system, interval-parameter multi-stage stochastic programming model was constructed and improved to consider effect of sensitive index of various stages and water irrigation on crop production, which introduced water sensitivity index weights and made a case study over rice at different growth stages in Heping irrigation area.The study area of this paper had two water sources: the surface water and the ground water, which also could be divided into three different projects by the water intake mode: water diversion project, water lifting project and well irrigation project.At the same time, Liuhe reservoir was taken as a water external source, where all the water system constituted a complex multi-water source supply system.In this study, four stages of rice growth were selected as the research period, i.e.tillering stage, jointing stage, heading stage and milk stage.The water sensitive index weight coefficients in each growth stage were 0.37, 0.46, 0.11 and 0.06 respectively.Inflow level of different growing stage was random variables and closely related to hydrological factors such as rainfall and runoff, hence the probability density function was introduced to represent uncertainty, and discrete interval was used to show other hydrologic and economic uncertainty.Multi-stage stochastic programming model could allocate water between different phases and different growing stages under a series of inflow level.Because of the uncertainty of inflow water, a four-period（five-stage）scenario tree and improved interval-parameter multi-stage stochastic programming model were used to carry out dynamic distribution of water in multiple stages of growth.Research results showed that in the context of different inflow level, managers could determine the water sensitive index of crop growth in different stages in accordance with the weight coefficient in each growth stage.The greater weight coefficient of the water sensitive index was, the greater the impact of water shortage had on the output, hence it belonged to the key water requirement stage; the smaller weight coefficient of the water sensitive index was, the smaller the impact of water shortage had on the output, hence it belonged to the non-key water requirement stage.When inflow water was excessive, excess water could be allocated to the next stage; when inflow water was insufficient, managers needed to seek a trade-off between reducing irrigation water and increasing transfer water.Tillering stage（t=1）and elongation stage（t=2）belonged to the key water requirement stage, managers wanted to fully satisfy the water needs of crops to ensure production, hence, in these two growth stages, no water deficiency existed, water deficiency value was 0.In different inflow level, when the irrigation water could not meet the demand for water, water supply project would transfer water from external water sources to meet the distribution targets in various growth stage; heading stage（t=3）and milk stage （t=4）belonged to non-key water requirement stage, so water deficiency had little effects on crop yield, and water supply project would make water deficit choice.When inflow level was not determined, it would take a lot of risk to meet the high water demand, and also increase the punishment of water deficiency; as for the low water demand, it took less risks, meanwhile, the punishment and water use benefit was also lower, which means water supply, risk and economic benefits are interwoven with each other.Through the analysis of optimal allocation of water supply project, the relationship between external water and irrigation water supply quantity, this paper realized the dynamic distribution of multi-water source irrigation system.This model can ensure the crop yield when the irrigation water resources are rationally configured in the growing period of the crop, and effectively avoid the waste of water resources, and improve the efficiency of irrigation water, which is of great significance for sustainable use of water resources.

Keywords:models; irrigation; crops; multi-water source in irrigation area; uncertainty; interval-parameter multi-stage stochastic programming model; optimal allocation

作者简介：付强，男，辽宁锦州人，教授，博士生导师，主要从事农业水土资源系统分析、冻融土壤水热作用机理等方面研究。哈尔滨东北农业大学水利与建筑学院，150030。Email：fuqiang0629@126.com。

基金项目：国家自然科学基金（51479032，51279031）；水利部公益性行业科研专项经费项目（201301096）；黑龙江省高校长江学者后备支持计划项目；黑龙江省水利厅科技项目（201318，201503）。

收稿日期：2015-08-17

修订日期：2015-11-06

中图分类号：TV213.9

文献标志码：A

文章编号：1002-6819（2016）-01-0132-08

doi：10.11975/j.issn.1002-6819.2016.01.018