基于Split-Bregman方法的稀疏角度CT重建算法研究

张丹丹

(中北大学 信息探测与处理技术研究所,山西 太原 030051)



基于Split-Bregman方法的稀疏角度CT重建算法研究

张丹丹

(中北大学 信息探测与处理技术研究所,山西 太原 030051)

摘要：离散梯度变换已被广泛地用作稀疏算子，相应的全变差(TV)最小化方法也被用于基于压缩感知(CS)的CT重建中.与此同时Split-Bregman算法在求解L1正则化问题方面引起了很大关注，此方法对原来的L1正则化问题引入一个分裂变量后利用Bregman迭代求解.本文将Split-Bregman方法用于稀疏角度CT重建，并与传统的SART和基于SART的软阈值算法(STF-SART)进行比较，最后用Head模型作为测试模型进行仿真实验，实验结果表明：对于稀疏角度CT重建问题，TV正则化(STF-SART和Split- Bregman)算法明显优于传统的SART算法，且Split-Bregman算法在收敛速度和重建图像质量方面又优于STF-SART算法.

关键词：离散梯度变化；压缩感知；稀疏角度CT；TV最小化；Split-Bregman算法

0引言

在医学CT扫描过程中，过量的X射线照射会对接受扫描的患者造成一定的危害性，故需要在保证成像质量的前提下尽可能降低X射线的辐射剂量.稀疏角度CT是降低X射线辐射剂量的一种有效手段，该方法在CT扫描过程中将只针对均匀分布的稀疏角度进行投影采样[1].但少量的投影数据并不满足奈奎斯特采样定率，若采用传统的重建算法，往往得不到高质量的图像[1-3].

随着压缩感知(CS)理论的发展稀疏角度CT重建问题有了很大进展.该理论表明若原始信号或图像在适当的变换域内具有稀疏表示，则可由少量投影重建图像[4].离散梯度变换(DGT)是最为常用的稀疏算子之一，其L1范数被称为TV，相应的TV最小化方法也被用于基于CS的CT重建中，包括稀疏角度重建[5].该问题的关键是如何在投影数据的约束下最小化TV.

2009年，Yu等人使用梯度下降法进行TV最小化，具体做法是先用经典算法对图像进行更新，然后用梯度下降法调整TV以实现TV最小化[6].2010年，Yu和Wang应用软阈值滤波框架，通过构建DGT的伪逆变换将软阈值滤波算法用于实现TV的最小化[5,7].与此同时，Split- Bregman算法在求解L1正则化问题方面引起了很大关注.此方法对原来的L1正则化问题引入一个分裂变量后利用Bregman迭代求解.它将目标函数的L1和L2范数部分“分裂”为多个子问题，该算法的有效性主要依赖于子问题的合理求解[8-9].本文基于TV最小化将Split-Bregman算法用于稀疏角度CT图像重建.

2基于TV最小化的CT重建模型

在医学成像领域，DGT已被广泛用作稀疏算子.一个二维图像f=(fi,j)I×J的DGT定义为：

(1)

相应的TV定义为：

(2)

基于TV最小化的CT图像重建问题可以表示为：

min‖f‖TV，s.t. ‖Af-Y‖≤ε

(3)

其中A是投影矩阵，Y是投影数据，ε是测量误差.

通过引入惩罚项，问题(3)可转换为无约束凸最小化问题：

(4)

其中μ是惩罚参数.

该问题的求解通常可分两步：第一步用经典迭代算法(如SART)进行重建：

(5)

其中f=(fj)J′1∈J是二维图像f=(fi,j)I×J的另一种表示形式，是迭代次数，0<λk<2是一个自由松弛因子；第二步在迭代框架下最小化图像的TV.

3Split-Bregman算法

式(4)表示的CT重建问题的Split-Bregman算法的主要步骤可以概括如下.首先引入两个新的变量将式(4)转换为：

(6)

然后引入惩罚项，将(6)转换为：

(7)

(7)可由Bregman迭代求解：

(8)

(9)

(10)

(8)可由交替方向乘子法(ADMM)交替迭代更新f和d：

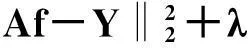
第一步可使用各种优化方法，考虑到CT重建矩阵A的特殊性，用最速下降法解决[10]：

fk+1=fk-αkgk

(11)

(12)

第二步可通过广义收缩公式求解：

(13)

(14)

基于Split-Bregman算法的CT重建的具体流程为：

S2：使用(11)执行梯度下降法；

S3：计算中间变量dx，dy，bx，by；

S4：转到S2，直到满足停止标准.

3实验设计及结果分析

实验选取Head模型进行试验，模型的大小为256×256，扫描方式为圆轨迹扇束扫描，扫描半径为500 mm，探测器包含320个探元，扇角为0.49弧度.实验对Head模型在[0,2π)范围内均匀采集90个角度下的投影数据，使用Split-Bregman算法进行重建，并与传统的SART算法和STF-SART进行比较，迭代200次的重建结果如图1所示.为了进一步验证三种算法对噪声数据的稳定性，对投影数据加入N(0，0.022)信噪比为38.2 dB的高斯噪声，重建结果如图2所示.另外为了定量地评估三种算法的性能，采用均方误差(MSE)和结构相似性(SSIM)作为评判标准，结果如表1所示.可以看出，对于稀疏角度CT重建，传统的SART算法重建的图像出现过平滑现象，TV正则化(STF-SART和Split- Bregman)算法重建图像的质量明显优于传统的SART算法，且Split-Bregman在收敛速度和重建图像的质量方面又优于STF-SART.这一结论同样适用于噪声投影数据的情况.

图1　三种算法对无噪声投影迭代200次的重建结果

图2　三种算法对噪声投影迭代200次的重建结果

算法SARTSTF-SARTSplit-BregmannSART-噪声STF-SART-噪声Split-Bregman-噪声MSE0.16480.15520.11200.19020.18560.1255SSIM0.49660.53450.67150.46360.49340.6103

4结论

针对稀疏角度CT重建问题研究了Split-Bregman算法在TV最小化方面的应用，并通过仿真实验与SART和STF-SART进行了比较.实验结果表明，对于稀疏角度CT重建，TV正则化(STF和Split-Bregman)算法明显优于传统的SART算法，且Split-Bregman算法在收敛速度和重建图像质量方面又优于STF-SART算法.后续研究工作将基于GPU或者使用有序子集方法等对Split- Bregman算法进行加速.

参考文献：

[1]吴长岳, 孔慧华.基于Lp算子的CT迭代重建算法研究[J].核电子学与探测技术, 2014, 34(4): 509-512.

[2]阙介民, 王燕芳, 孙翠丽, 等.基于不完备投影数据重建的四种迭代算法比较研究[J].CT 理论与应用研究, 2012, 21(2): 169-178.

[3]郑源彩.基于压缩感知理论的有限角度投影重建算法研究[D].中北大学, 2013.

[4]Donoho D L.Compressed sensing[J].Information Theory, IEEE Transactions on, 2006, 52(4): 1289-1306.

[5]Yu H, Wang G.A soft-threshold filtering approach for reconstruction from a limited number of projections[J].Physics in medicine and biology, 2010, 55(13): 3905.

[6]Sidky E Y, Kao C M, Pan X.Accurate image reconstruction from few-views and limited-angle data in divergent -beam CT[J].Journal of X-ray Science and Technology, 2006, 14(2): 119-139.

[7]吴俊峰, 牟轩沁, 张砚博.一种快速迭代软阈值稀疏角 CT 重建算法[J].西安交通大学学报, 2012, (12): 24-29.

[8]Yin W, Osher S, Goldfarb D, Darbon J.Bregman Iterative Algorithms for $ell_1$-Minimization with Appli- cations to Compressed Sensing,[J].SIAM J.Imaging Sci.,2008,1(1):143-168.

[9]Cai J F, Osher S, Shen Z.Linearized Bregman iterations for compressed sensing[J].Mathematics of Computation, 2009, 78(267): 1515-1536.

[10]Nocedal J, Wright S J.Line search methods[J].Numerical optimization, 2006: 30-65.

[责任编辑：王军]

Study on Split-Bregman algorithm for sparse-view CT reconstruction

ZHANG Dandan

(Institute of Signal Capturing Processing Technology, North University of China,Taiyuan 030051, China)

Abstract:The TV minimize technique which corresponds to Discrete Gradient transform is widely used in the CT reconstruction basing on CS, including sparse-view reconstruction based on compressed sensing(CS).Meanwhile, Split-Bregman algorithm has caused great concern in solving L1regularization issues, this method first introduces a split variation to the original regularized problem and then use Bregman iterative solve it.In this paper, we apply the Split-Bregman approach to reconstruct an ROI for the CS-based sparse-view CT reconstruction, and combined with the traditional SART algorithms and soft thresholding algorithm based on SART (STF-SART) .Finally Head model is applied as a test model to the simulation experiment，and the results shows that: for sparse-view CT reconstruction , TV regularization (STF-SART and Split- Bregman) algorithms outperform conventional SART algorithm, and Split-Bregman algorithm is superior to STF-SART algorithmsn terms of convergence speed and reconstructed image quality.

Key words:gradient descent algorithm; compressive sensing; sparse-view CT; TV minimization; Split-Bregman algorithm

中图分类号：TP391.41

文献标识码：A

文章编号：1672-3600(2016)03-0013-04

作者简介:张丹丹(1991-)，女，山西临县人，中北大学理学院硕士研究生，主要从事图像重建研究.

收稿日期：2015-10-20