立足“四多”,培养学生“四能”
江苏淮安市淮海路小学教育集团(223001)汪静静
立足“四多”,培养学生“四能”
江苏淮安市淮海路小学教育集团(223001)汪静静
[摘要]在小学数学教学中,培养学生的问题解决能力是核心目标,这一目标也是课程改革明确提出的要求。根据教学实践,提出要立足多表征、多维度、多层次、多优化的“四多”模式,培养学生发现问题、提出问题、分析问题、解决问题的“四能”。
[关键词]培养目标四能培养策略研究
在小学数学教学中,教师的重要职责就是要培养学生发现问题、提出问题、分析问题和解决问题的能力。因此,教师应当立足“四多”,即多形式呈现问题、多表征提出问题、多角度思考问题、多优化解决问题,从这四个方面实施“多”向教学,以此培养学生发现问题、提出问题、分析问题、解决问题的“四能”。
一、立足多形式呈现,培养发现问题的能力
课程标准在原来“分析问题”和“解决问题”两种能力培养的基础上,增加了“发现问题”和“提出问题”两种能力的培养。何谓发现问题的能力?对于小学生来说,就是指发现困惑,在显而易见的地方发现“问题”的能力。这种“问题”是广度的问题,可能是以前不了解的东西,也有可能是书本上没有的新观点、新方法等。因而,在教学中,教师要把握时机,多维度呈现素材,给学生建构直观形象的数学表象,激发学生的好奇心,引发学生的探究动机。
例如,在教学“周长的认识”时,为了让学生深入理解周长这个概念,可创设多种形式的问题:首先,让学生从生活中寻找实物,并指一指、说一说这个实物的周长,说清楚大小范围,学生从数学课本、树叶、文具盒入手,一边用手比划,一边说明,从而对周长有了初步的认知;其次,让学生动手描一描、画一画,画出周长的曲线,学生在描画树叶和礼盒的周长过程中,知道不能留空,由此深入理解周长这个概念的内涵,抓住了“封闭”和“一周”这两个关键点,对周长有了深刻的把握;最后,让学生动手量一量、测一测,学生通过测量正方形的周长,体会到要只要量出这个正方形的一条边的长度,然后再乘4,就能得到正方形的周长,因为正方形四条边都相等。
教师通过多种形式的问题呈现,让学生对数学概念的认知由浅入深,逐步深入,由此加强了学生对数学问题的多元认知,使学生能够抓住数学知识的本质,培养了学生发现数学问题的能力。
二、立足多表征引导,培养提出问题的能力
何谓提出问题的能力?对于小学生来说,它是指将某些问题运用数学的形式表达出来,也就是将发现的问题数学化的能力。教学中,教师要立足多元表征引导,带领学生运用数学语言、数学符号对数学问题做出恰当的数学抽象,激活学生头脑中的知识经验,培养学生提出问题的能力。
例如,有甲乙两个长方体水箱(如图1),甲水箱长、宽、高分别是40厘米、30厘米、20厘米;乙水箱长、宽分别为30厘米、20厘米。乙水箱中装有24厘米深的水,而甲水箱中没有水。现在要将乙水箱中的水向甲水箱中倒一部分,使这两个水箱的水的深度相等。求这时水箱中水的深度。
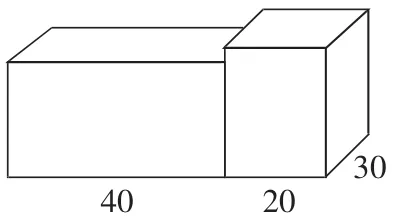
图1
首先,我引导学生自主探究。通过审题和了解问题结构,有学生认为,可将两个长方体拼成一个底面积是60×30=1800(平方厘米)的不规则物体,乙长方体内水的体积为30×20×24=14400(立方厘米),因为水的高度相等,由此可以得到高度为14400÷1800=8(厘米);也有学生认为,可先分别求出甲乙两个长方体的底面积“40× 30=1200;30×20=600(厘米)”,得到甲长方体底面积是乙长方体底面积的2倍,原有乙长方体内水的体积是30× 20×24=14400(立方厘米),根据已知条件中甲乙两个水箱的高度相等,因而倒水后的甲水箱内水的体积是乙水箱内水的体积的2倍,推理原有乙水箱内水的体积是现有乙水箱内水的体积的3倍,可以得到14400÷3=4800(立方厘米),再根据长方体体积除以底面积得到高为4800÷600=8(厘米);还有学生认为,甲长方体底面积是乙长方体底面积的2倍,甲乙两个长方体水的深度相等,所以现在乙水箱内水的高度是原来高度的三分之一,也就是24÷3=8(厘米);更有学生提出,可以用方程来解答,设水的高度为x厘米,得1200x+600x=30×20× 24=14400,x=8;还有学生提出,甲乙两个长方体的宽相等,水的高度也相等,甲的长度是乙的长度的2倍,由此可知,体积也是2倍的关系,只要将原来乙长方体里的水沿高平均分成3份,这样水的高度就是原有高度的三分之一。
通过教师的引导,学生采用文字表征、数式表征、图表表征、模型表征等多种形式解决了问题,折射出个性思维的光彩,培养了自身的数学表达能力。
三、立足多角度思考,培养分析问题的能力
著名数学家弗莱登塔尓认为,数学教学的本质,是要教给学生不同的思考方法,让学生聚焦问题,自主探究数学问题,学会分析问题。教师要立足培养学生多角度思考问题的能力,带领学生展开自主探究,发展学生的数学思维,培养学生分析问题的能力。
例如,在教学“认识整体的几分之一”时,我从多个角度展开,让学生深入理解几分之一的深刻内涵。角度一,将一块饼平分给4个猴子,每只小猴分得几分之几?学生认为,将一块饼平分给四个猴子,每份是块饼,每份是这块饼的;角度二,将一盒桃子(共4个)平均分给4个猴子,每只小猴分得几分之几?学生认为,将一盒桃子(4个)平分成4份,其中一份是1个桃,这一份是整体的;角度三,有8、12、16个桃子分别要平均分给4个猴子,每个小猴分得几分之几?学生认为,不管桃子有多少个,只要平分成4份,每份就是这些桃的;角度四,将12个桃子平均分给2个或3个猴子,每只猴子分得几分之几?这些分数有什么不同?学生认为,同样多的桃,平均分的份数不同,用来表示每份的分数也不同,关键是要看平均分成了几份。
教师借助多重比较,帮助学生从多个角度进行探究,学生对“整体的几分之一”有了深入认识后分析问题的能力自然得到提升。
四、立足多直观优化,培养解决问题的能力
在小学数学中,教师要立足直观优化,给学生创设直观的教学情境,让复杂的问题简单化,抽象的问题具体化,以此培养学生解决问题的能力。
例如,在教学“解决问题的策略:画线段图”时,对于教材中的问题“绿花有12朵,黄花是绿花的2倍,红花比黄花多7朵,红花有多少朵?”学生已经有了初步了解,于是我引导学生画出直观图,有学生画出了图2。
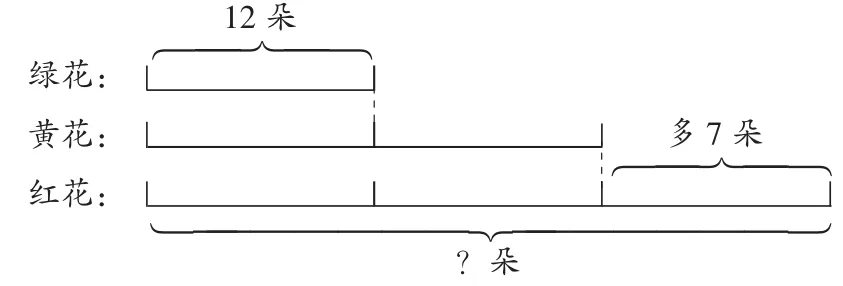
图2
学生讨论后一致认为线段图中的“多7朵”画得太长了,我问道:“如何优化呢?”学生先认为要画得短一些,我追问:“短多少呢?”学生经过思考,发现画得比表示绿花12朵的线段长度的一半多一些就可以了,由此得到图3。
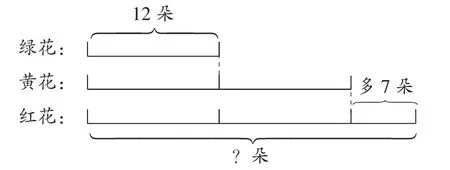
图3
通过教师的引导,学生学会梳理复杂的数量关系,并经过多重优化,得到有效的线段图,从而大大提升了解决问题的能力。
总之,学生“四能”的培养并非一朝一夕就能实现,而是一个长期的过程,教师只要立足“四多”,一定能够让学生善于发现问题,学会提出问题,从而获得分析问题和解决问题的能力。
(责编童夏)
[中图分类号]G623.5
[文献标识码]A
[文章编号]1007-9068(2016)05-075

