“好问题”与“好课堂”——以“长方形和正方形的认识”教学为例
江苏海安县实验小学(226600)李建梅
“好问题”与“好课堂”——以“长方形和正方形的认识”教学为例
江苏海安县实验小学(226600)李建梅
[摘要]数学是抽象的,并具有高度概括的特征。如何让纯粹的数学转化为儿童可接受的童化数学,离不开教师对儿童认知过程的深入分析,对问题的精心预设。基于本质、驱动思维、指向素养的问题,才是好问题。在具有统摄功能的核心问题驱动下,引领儿童思维攀高,驱动课堂向纵深进发。
[关键词]核心问题数学本质学科素养
【课前思考】
一、认识长方形和正方形应经历怎样的学习过程?
学生在一年级上学期学习了立体图形之后,下学期便开始正式接触长方形和正方形。正式接触长方形和正方形之前,学生对它们的认识还停留在直观感知层面:会找寻,能识别,在钉子板上围,利用方格纸画……缺乏对长方形和正方形本质特征的关注。三年级的学习便提出了对长方形和正方形的特征进行抽象概括的要求,而如何在唤醒学生感性经验的同时加强对边和角的关注是本节课的难点,引导学生从对个别图形的研究转到用更多图形进行验证,实现感知到思维的提升则是本节课的重点。
二、怎样的核心问题能驱动整个学习活动?
问一年级的学生:“长方形、正方形长什么样?”他们会有各种各样的表达方式:画个草图,拿个实物,盖个印章……直观形象、简单明了地诠释自己的理解。三年级学生研究的“长方形和正方形的特征”不过是对“长方形、正方形长什么样”更为理性的表达。对于还处于从直观形象思维向抽象形象思维过渡的三年级学生而言,笔者认为用“长方形、正方形长什么样”的这个核心问题来驱动本节课的学习是适宜的,它不仅通俗易懂,直抵本质,而且可以实现对前后两个阶段不同水平学习的整体观照。
【教学规划】
一、在直观操作中聚焦边与角的特征
核心问题:长方形、正方形长什么样,你会表示吗?
1.画一画
(1)谈话:今天我们研究的内容是“长方形和正方形”(板书:长方形和正方形),在你的脑海里“长方形、正方形长什么样?”不妨选择一个把它画下来。(学生自己选择是在练习纸的空白处、横线上还是方格上画)

(2)思考:你们选择在哪里画长方形或正方形?为什么?
(3)小结:大家在画长方形或正方形的时候已经留意到边(板书:边)是直直的,这是它们的一个重要特征。
【思考:“你们选择在哪里画长方形或正方形,为什么?”看似不经意却是关键性的一问,触动了学生敏感的神经,通过在“选地方画图”的分析中意识到横线比空白好,方格为最好,从而引发学生对长方形、正方形边和角的关注,将以往学生无意识的行为转化为有意义的学习活动。】
2.摆一摆
(1)谈话:我们不但能画出长方形、正方形,我们应该还能用小棒摆出这两种图形。如果给大家提供以下3种规格的小棒,你能摆出长方形或正方形吗?

(2)在学生选择前设问:如果摆长方形你打算选择怎样的小棒?
(4)小结:看来摆长方形或正方形时,我们不仅要关注边,还要关注角。(板书:角)
(5)让学生在大脑中构图,说出其他摆法。
【思考:“如果摆长方形你打算选择怎样的小棒”强化学生对长方形对边相等的感知,对学生操作过程中出现的必然现象进行追问:“他在调整什么?想调整成什么角?”唤醒了学生的潜意识,很自然地引发学生对长方形的角的关注。】
3.比一比
这几个长方形的边和角有什么共同的地方?正方形呢?(板书:对边相等四条边相等四个都是直角)
【思考:用3种不同规格的小棒摆一摆,既是一次思维的开放,也是将相似结构的图形进行归纳比较的重要素材。“这几个长方形的边和角有什么共同的地方?”再次带学生回归到对图形本质特征的关注上。】
二、在操作验证中概括边与角的特点
核心问题:长方形、正方形长什么样,你会研究吗?
1.谈话与设问
应该说“四个角都是直角,对边相等”是这3个长方形的特征,“四条边相等”是这几个正方形的特征。是不是所有的长方形和正方形都有这样的特点?(板书:?)我们还需要进行怎样的研究?
2.操作验证
(1)谈话与设问:为了研究的方便,老师给你们每个小组(4人一组)准备了一个信封,信封里装着大大小小的2个长方形和2个正方形。每个人选择其中一个图形试着验证给小组的其他成员看。你打算如何进行验证?
(2)研究操作导图:从下面这幅连环画你能否看懂如何“量一量、折一折、比一比”?

(3)操作后重点反馈:用量的方法能够证明这些正方形四条边相等,怎样用折的方法证明?
(4)反思小结:抽象概括,擦去原有板书的“?”。
【思考:将研究的对象从特殊走向一般是小学生应该习得的一种重要方法。“你打算如何进行验证?”是学生对自己的一次叩问,也是对小组合作的一次需求。教材中的操作导图,不妨用连环画的方式呈现,引导学生用看图说话的方式“逼迫”其自我提炼操作要领,这样能大大减少接下来操作过程中的盲目无效劳动。“怎样用折的方法证明?”不仅是一次难点击破,还是对操作方法多样性的一次补充。】
三、在综合运用中巩固边与角的特点
核心问题:长方形、正方形长什么样,你会表达吗?
1.判断说理
信封里装着四边形,它是长方形或正方形吗?(请用“一定、可能、不可能”描述)
称取3份的30%HNO3改性活性炭和3份无改性活性炭0.08g于12个250mL具塞锥形瓶内,分别倒入150mL 10.0mg·L-1的DBP溶液,分成2组分别将2 组具塞锥形瓶置于 30、35、40℃的 3 种 150r·min-1气浴恒温振荡器中振荡3h。不同温度下DBP的去除率见图3。

2.填一填、认一认
(1)你能根据已知边的长度推想出其他边的长度吗?
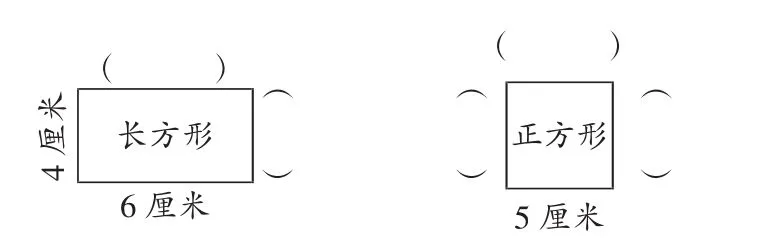
提示:在数学上这些边分别叫什么?可以自己尝试取名,也可以问问同伴,还可以自学课本哦!
3.画一画
在方格纸上画一个长为8厘米,宽为6厘米的长方形,或者是边长为3厘米的正方形。

【思考:这是三道巩固长方形和正方形特征的基础性练习。判断说理环节试图引导学生用自己的语言阐述原因,凸显数学本质。填一填、认一认既是对边的特征的强化,也是引出各条边名称的契机。】
用一张长为8厘米、宽为6厘米的长方形纸折成一个最大的正方形。最大的正方形的边长是多少?你打算怎样操作?(在头脑中思考;借助图形思考;动手折一折)
【思考:面对不同思维水平的学生,教师还应该尊重学生的不同选择:优生跳一跳——在头脑中想象过程;学困生有方法依靠——动手折一折;一般学生有策略——借助图形思考。让不同水平的学生都能获得不同的发展,让每个学生都能自主实现认知的伸展与跳跃。】
5.你知道吗?
这包餐巾纸的规格是:200mm×135mm×2层×200抽/包,你知道其中的200mm×135mm是什么意思吗?

【思考:数学总在日常生活中有着广泛的应用,捕捉一些与课堂学习同步的素材,适当引进课堂,不仅能丰富学习素材,而且能提高学生的数学敏感度。】
【课后说课】
本课以“长方形、正方形长什么样”为核心问题,贯穿和统摄全课,驱动学生一步步完成认知水平的三级跳:直观表示——主动研究——积极表达。三次活动恰好对应三个层次的教学目标:直观感知——验证概括——具体运用。为了促进核心问题的深入理解,教师“步步为营”,精心设计了一系列关键性问题,每一次设问,或直指数学本质,或关乎数学素养。在核心问题的驱动下,学生的经验被唤醒,热情被点燃,思路被打开……学生对长方形和正方形的认识从原有的边是“直直的”,角是“方方”的感性层面提升到“对边相等”“四条边相等”和“四个角都是直角”理性层面。作为核心素养内隐特质的数学思考和数学态度都得到了有效关注。研究千千万,起点在一问!作为教师就应该在课堂设问上下工夫,用问题引领,驱动课堂向纵深进发!
(责编金铃)
[中图分类号]G623.5
[文献标识码]A
[文章编号]1007-9068(2016)05-010

