基于形态滤波与EEMD组合方法的声发射去噪**

席剑辉 许 廿

(沈阳航空航天大学，辽宁 沈阳 110036)

基于形态滤波与EEMD组合方法的声发射去噪**

席剑辉①许 廿②

(沈阳航空航天大学，辽宁 沈阳 110036)

针对声发射信号传递和采集过程中干扰噪声多态性、随机性等问题，研究形态滤波与集合平均经验模态分解(EEMD)的组合方法，从空间域和时频域不同角度对信号进行降噪处理。首先采用加权级联形态滤波，对闭开和开闭运算进行适当搭配，通过权值调整有效滤除声发射信号的尖峰脉冲干扰；然后应用EEMD对处理后的信号进行分解，依据相关系数去除虚假分量并重构信号，提取信号特征信息。对模拟声发射信号和实测声发射信号的仿真结果说明了此方法的有效性。

声发射；形态滤波；EEMD；去噪

声发射检测作为一种动态无损检测手段，通过监听被测器件因结构变化、表面损伤等原因而发射出来的声波信号，分析信号特征，进而判断声源位置及物理状态，为准确评价被测器件的健康工作状态提供有效信息。因为声发射是故障结构本身发出的高频应力波信号，不易受周围环境低频噪声的干扰，是对振动检测方法的有益补充。但声发射信号在传递和采集的过程中也会受到多种宽频或高频噪声干扰，如白噪声、随机脉冲干扰、电磁尖峰脉冲干扰、由放大器或传感器引入的尖脉冲等。这些噪声具有多态性和随机性特征，噪声频带与声发射信号频带重叠，极大地影响有效信号的特征提取，因此信号降噪成为声发射测试及应用研究的重要内容。

形态滤波法[1-2]基于积分几何和随机集理论，不同于时频域分析方法，能够在不改变故障信号几何特征的情况下滤除比结构元素小的噪声成分。郝如江等人[3]通过监测轴承故障点与其他运动部件的滚动接触而产生的周期性声发射信号，应用形态滤波提取出声发射信号中的特征频率。李修文等人[4]针对低速轴承信号的降噪过程，应用形态滤波消除声发射信号中的有色噪声，对信号中的高斯白噪声则采用最小二乘方法进行拟合平滑。可见形态滤波在抑制随机白噪声方面表现不足[4-5]。而且，当噪声较大时，特征信号的形态特征扭曲严重，也很难进行合适的结构元素匹配。基于辅助白噪声实现降噪的EEMD算法[6-7]可以很好地弥补这一不足，将信号从高频到低频分解至有限个反映不同振动模态的本征模态函数(IMF)，从而分离高频信息和干扰。

此方法主要针对采集的高频声发射信号，将形态滤波和EEMD方法组合从空间形状特征和时频域特征两个角度对信号进行降噪，可以滤除信号中包含的不同类别的噪声。首先采用级联的形态滤波器对原始声发射信号进行去噪；然后利用EEMD分解形态滤波处理后的声发射信号；选择相关系数较高的本征模态分量重构信号并分析，达到去噪和特征提取的目的。

1 形态滤波与EEMD的组合降噪

1.1 方法流程

声发射信号传递和采集过程往往不可避免地混入各种各样的噪声，采用单一的去噪方法不易准确提取有效信息。本文首先通过数学形态学方法滤波，研究信号结构特征，分离脉冲干扰；接着利用EEMD研究声发射信号的时频特性，将信号分解为一系列的IMF分量，有效分离出声发射信号中含有的随机噪声或宽频噪声成分；然后通过相关系数准则舍去IMF中的虚假分量，选择相关系数较高的IMF分量重构信号；最后进行特征提取和去噪效果分析，如频谱分析、信噪比计算等。图1所示为声发射源信号降噪流程图。

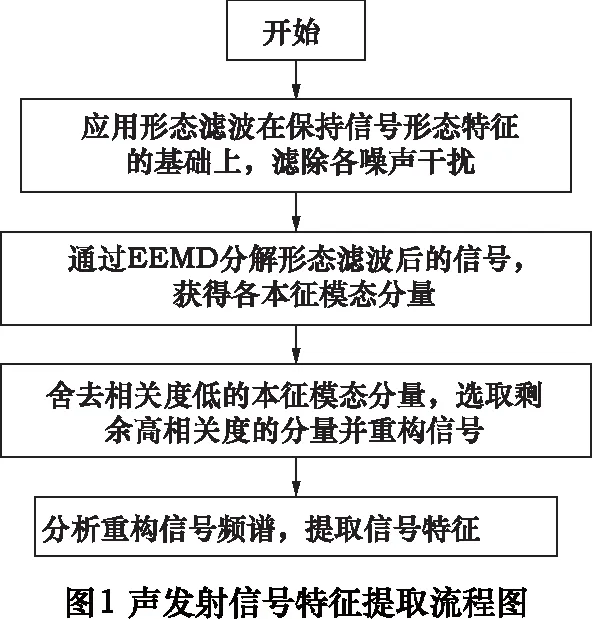
1.2 形态滤波

形态滤波基本思想是通过所设计的小结构元素在信号中逐段移动，对信号进行匹配，达到提取信号信息、保持细节特征和抑制噪声的目的[8]。

1.2.1 加权级联形态滤波器

形态滤波的4种基本运算是膨胀、腐蚀、开和闭。设定声发射信号为f(n)，n= 0，1，…，N-1，N为采样点数。定义结构元素序列为g(m)，m= 0，1，…，M-1，M为结构元素宽度，且N≥M，则f(n)关于g(m)的腐蚀和膨胀分别定义为[9-10]：

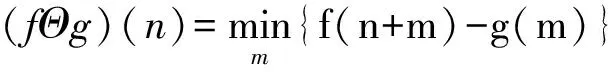
(1)

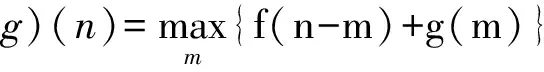
(2)

f(n)关于g(m)的开运算和闭运算分别定义为：

(f∘g)(n)=(fΘg⊕g)(n)

(3)

(f·g)(n)=(f⊕gΘg)(n)

(4)

开运算可以削弱声发射信号中的正脉冲噪声，消除散点、毛刺；闭运算具有扩张性，可以抑制声发射信号负脉冲噪声，填平断点。两种运算合理搭配可同时发挥两种算子的优势，滤除正负脉冲噪声。因此设定加权级联形态滤波器为：

y(n)=α·Foc(f(n))+(1-α)Fco(f(n))

(5)

其中

Foc(f(n))=(f∘g·g)(n)

(6)

Fco(f(n))=(f·g∘g)(n)

(7)

α为加权因子，0 <α<1；y(n)为滤波结果。适当调整α值，可以调整不同算子的滤波贡献，改善滤波结果。

1.2.2 形态滤波中结构元素的选取

结构元素的形状和宽度对形态滤波效果的影响显著，信号基元只有与结构元素的形状和宽度相匹配才会被保留。典型结构元素有直线、三角形、椭圆形、正弦形及抛物线形等。其中直线形结构元素具有形状简单、计算方便等特点。根据Nikolaou等[11]的分析结果，本文采用直线形结构元素对声发射信号进行形态滤波。为了更好地保持信号形状的几何特征，设定结构元素幅值为零。

直线形结构元素的重要参数是宽度M，决定了滤波能够提取的脉冲个数。宽度M较小，细节匹配越好，脉冲个数提取越多，但混入的噪声信号也越多；宽度M较大，提取的脉冲个数较少，有效信号也可能被误滤除。本文根据Nikolaou等[11]分析结果，以滤波前后声发射信号的相关性达到最大作为选择准则，最终确定结构元素的宽度值。

1.3 EEMD降噪

EEMD是一种新的对于非平稳信号的分析方法，将信号分解成频率不同的各个IMF分量。利用高斯白噪声具有频率均匀分布的统计特性，在经过形态滤波的声发射信号中加入高斯白噪声，使声发射信号在不同频率尺度上具有连续性，弥补间断事件造成的尺度缺失，可以有效抑制模态混叠问题，使最终提取的IMF分量能够有效代表信号的一个内在特征模式。设形态滤波后的声发射信号序列为y(n)，EEMD方法分解信号的步骤为：

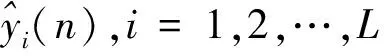
Step3 求u(n)和v(n)的均值m(n)：

m(n)=[u(n)+v(n)]/2

(8)

则

(9)

Step4 设定hk-1(n)是第k-1次的处理结果，k= 1，2，…，可得hk-1(n)的上包络线uk-1(n)和下包络线vk-1(n)，均值mk-1(n)为：

mk-1(n)=[uk-1(n)+vk-1(n)]/2

(10)

可得

hk(n)=hk-1(n)-mk-1(n)

(11)

根据本征模态函数条件判断hk(n)是否为IMF分量，若不满足则重复进行Step4处理信号，直到满足条件得到第1个IMF分量ci1(n)，即

ci1(n)=hk(n)

(12)

Step5 计算余量信号：

(13)

Step6 对余量信号重复Step2～5，共获得l个IMF分量cij(n)，j= 1，…，l。

Step7 重复Step1～6，对上述相应的IMF整体求均值：

(14)

其中cj(n)为第j个IMF分量。

因为每次分解随机添加白噪声，噪声之间不相关，式(14)对所有的IMF分量求平均会抵消噪声影响，最终获得有效的声发射信号IMF分量[12]。

2 仿真实例分析

2.1 模拟声发射信号去噪及其效果评价

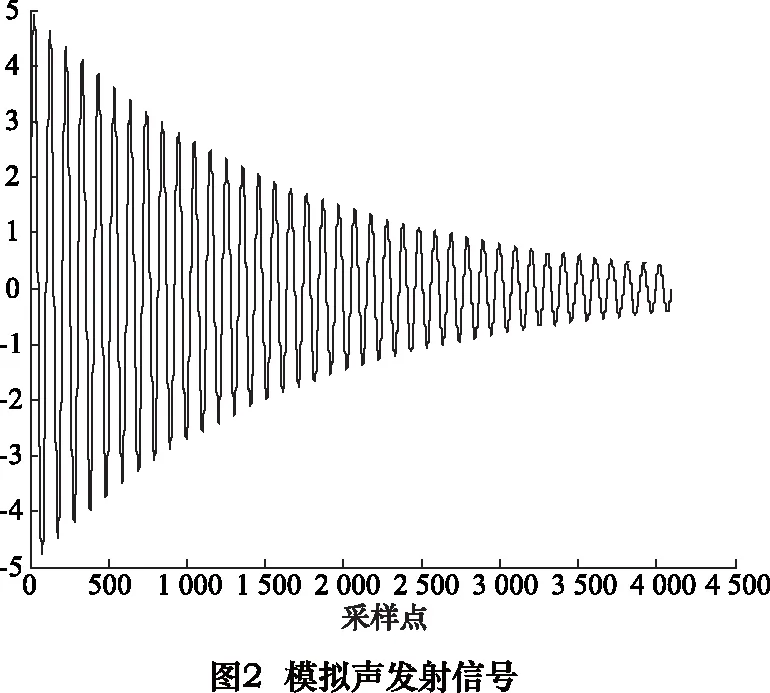
为验证本文方法的可行性，模拟声发射信号如式(15)，画出曲线如图2所示，可以看出该模拟信号具有声发射信号的周期性和衰减性。

x(t)=5e-2.5t×sin(2π×40t)

(15)

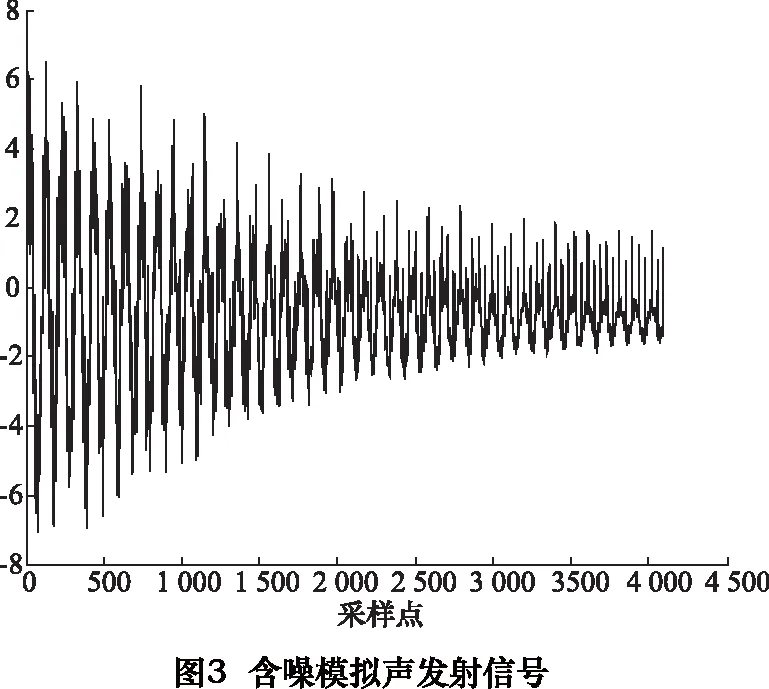
在信号中加入高斯白噪声σ(t)和100 Hz的方波信号s(t)作为模拟声发射信号，信号的信噪比为2.8 dB。仿真的目的是抑制高斯白噪声和方波噪声，提取信号特征。则带噪声的模拟声发射信号f(t)为

f(t)=x(t)+i(t)+s(t)

(16)

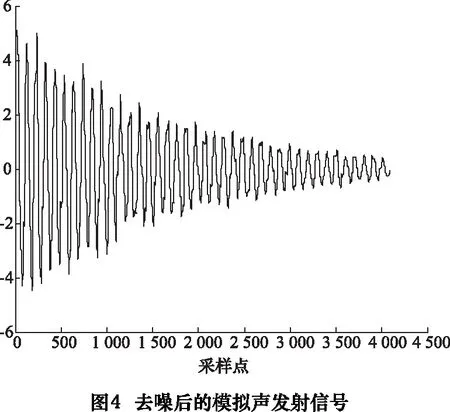
如图3所示。滤波效果通过信噪比来衡量。对原始信号进行形态滤波以及EEMD分解。其中α=1/2，结构元素长度M为11。图4为去噪后的时域波形。对比图2～4，可以看出滤波后的波形完整再现了理想原始信号的几何特征。说明对模拟声发射信号进行形态滤波和EEMD组合去噪取得了满意效果，能够很好的恢复原始波形。

图5和图6分别对应去噪前后信号的频谱分析图，可以看出信号40 Hz主要频率成分明显体现，而100 Hz噪声成分则大幅度衰减，高频白噪声也得到有效抑制和减弱。噪声抑制在高频部分显得尤为明显。依据时域图和频谱图的对比，验证了形态滤波和EEMD组合去噪方法的可行性。为接下来进行实测声发射信号去噪打下基础。

为定量分析组合方法的有效性，将带噪声模拟声发射信号进行形态滤波、EEMD单独去噪，以及组合方法去噪。3种方法去噪后的信噪比比较如表1所示。由表可知，形态滤波和EEMD组合的方法去噪性更好，能够显著提高信号的信噪比。

表1 各状态的信号信噪比对比

信号带噪声模拟声发射信号形态滤波去噪EEMD去噪组合方法去噪SNR/dB2．805．997．7710．97

2.2 声发射实测信号的去噪及其效果评价

基于以上仿真，将此方法应用到实测声发射信号中。图7a为滚动轴承模拟故障试验平台。实验过程声发射传感器位于轴承座的正上方，如图7b所示。并且在传感器与轴承座接触面之间填充耦合剂以减少声发射信号在传播时衰减能量。实验选用北京声华兴业科技有限公司的SAEU2S声发射系统作为前端采集设备。此次实验使用的是内圈损伤故障的滚动轴承，缺陷的宽度为1 mm。采样频率为1 000 kHz，采样长度为131 070，电动机转速约为1 000 r/min。

图8为轴承内圈故障运行时采集的声发射信号。对此声发射信号进行形态滤波和EEMD组合方法去噪，实现声发射信号的去噪和特征提取。经过大量仿真，计算滤波前后信号的相关性，选的结构元素长度为12，开闭-闭开运算级联权值α=3/4。

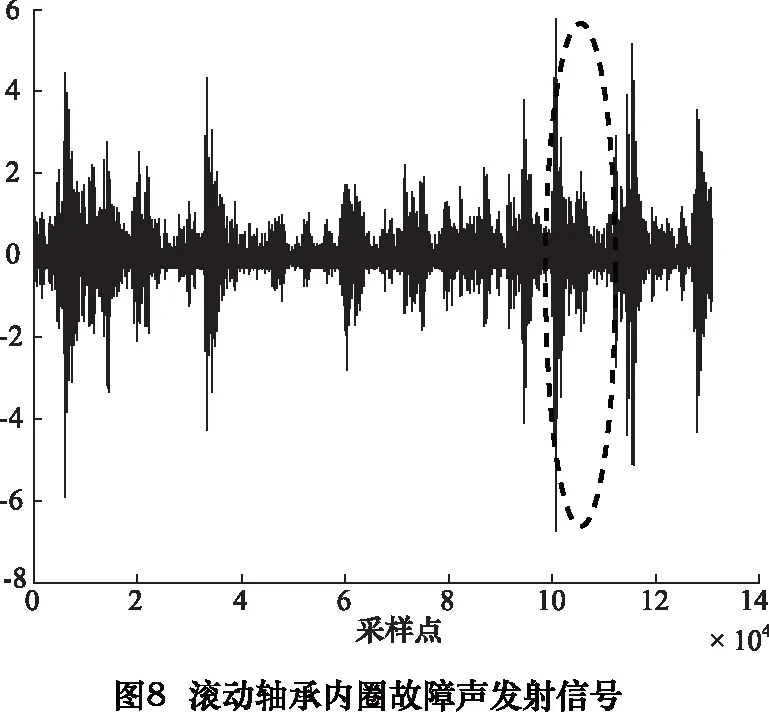
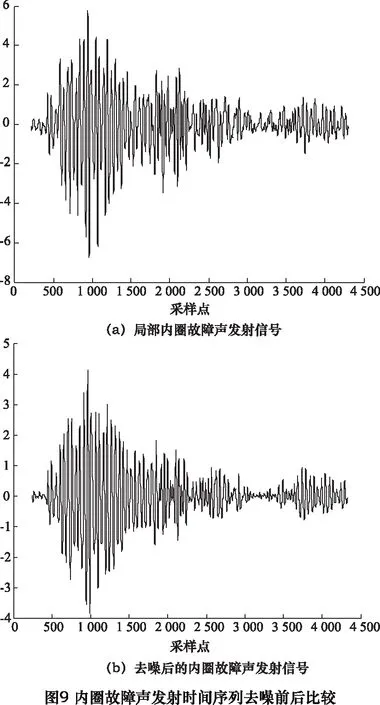
为更清晰地描述去噪效果，图9a给出内圈故障声发射信号的局部放大图，对应图8中圈出的第100 000到第104 095个采样点部分。该局部序列对应的去噪结果如图9b所示,可看出形状特征保存良好。

去噪前后声发射信号的频谱如图10所示，可知通过形态滤波与EEMD组合方法处理后，实测声发射信号中的高频随机噪声得到明显抑制。在内圈的缺陷频率附近存在着明显的峰值(80.31 Hz)，该频率一般被叫做基频，也是图10b中最大峰值所对应的频率。除了在基频附近存在峰值以外，在其倍频处(160.6 Hz)也存在着明显的峰值，并且幅值呈下降的趋势。经处理前后的声发射信号频谱图中的倍频比较看出，信号处理前的倍频处由于噪声干扰显示为152.6 Hz，而处理后倍频显示为160.6 Hz，可见处理后的信号频谱图更明显的体现了声发射信号特征。综上所述，形态滤波与EEMD组合的方法用于分析轴承故障和特征提取是有效的。

3 结语

为减少多种噪声对声发射源信号的影响，采用形态滤波和EEMD分解组合的方法进行信号去噪，并对声发射故障信号的特征提取。形态滤波可以在滤除噪声的同时不改变故障信号的几何特征，相当程度上减少了噪声对随后进行的EEMD分解的影响；EEMD对形态滤波预处理后的声发射源信号的各阶IMF分量中选取相关系数较高的模态分量重构信号，作为分析对象。对模拟和实测的故障声发射信号滤波，并进行频谱特征提取，验证了该方法的有效性，且效果良好又易于实现。

[1]Maragos P, Schafer R W.Morphological filters — Part II: Their relation to median, order statistic, and stack filters [J]. IEEE Trans on ASSP, 1987, 35(8): 1170-1184.

[2]侯高雁,吕勇,肖涵,等.基于EEMD自适应形态学在齿轮故障诊断中的应用[J].振动与冲击,2014,33(18):145-148.

[3]郝如江,卢文秀,褚福磊.形态滤波在滚动轴承故障声发射信号处理中的应用[J].清华大学学报：自然科学版, 2008(5)：812-815.

[4]李修文,阳建宏,黎敏,等.基于频域形态滤波的低速滚动轴承声发射信号降噪新方法[J].振动与冲击,2013,32(1)：65-68.

[5]徐元博,魏振东.形态滤波与EEMD在振动筛轴承故障诊断中的应用[J].轴承,2015(10)：41-44.

[6]Huang N E, Shen Z, Long S R, et al. The empirical mode decomposi -tion and the hilberts pectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995.

[7]Wu Z，Huang N E． Ensemble empirical mode decomposition: a noise-assisted data analysis method[J].Advances in Adaptive Data Analysis，2009，1(1) : 1-41.

[8]Serra J. Image analysis and mathematical morphology[M].New York:Academic Press,1982.

[9]曹莹,段玉波,刘继承.基于多尺度的形态滤波降噪方法[J].化工自动化及仪表,2015(11)：1202-1205.

[10]李向新,张颖,刘美容.基于数学形态学的正序基波谐波检测方法[J].电气开关,2014(02):20-24.

[11]Nikolaou N G，Antoniadis I A.Application of morphological operators as envelop extractors for impulsive-type periodic signals[J]. Mechanical Systems and Signal Processing, 2003, 17(6): 1147-1162.

[12]李辉,郑海起,唐力伟.基于EEMD和THT的齿轮故障诊断方法[J].振动、测试与诊断,2011,31(4): 496-500.

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

De-noising of acoustic emission signals based on the combination of morphological filtering and EEMD

XI Jianhui①, XU Nian②

(Shenyang Aerospace University, Shenyang 110136, CHN)

Aimed at the problems in the process of acoustic emission signal transmission and acquisition, such as the diversity and the randomness of the interference noise, a combination methodology of the morphological filtering and the ensemble average empirical mode decomposition (EEMD) was studied, then the signal de-noising was carried out from different angles of spatial domain and time frequency domain. Firstly, use the weighted cascaded morphological filtering, the close-open and open-close operations of which were appropriately matched, to effectively filter the peak pulse interference of acoustic emission signal by the weight adjustment. Then the EEMD method was used to decompose the processed signal. According to the correlation coefficient method, the false components could be removed and the signal could be reconstructed for extracting signal feature information. Simulation results from both the simulated and the practically measured acoustic emission signals were presented to illustrate the effectiveness of the proposed method.

acoustic emission; morphological filtering; EEMD; de-noising

*国家自然科学基金青年基金资助项目(60804025)；辽宁省教育厅科学技术研究项目(L2014069)及(L2013070)；沈阳市科技创新团队项目(src201204)

TH806;TH113

A

10.19287/j.cnki.1005-2402.2016.12.013

席剑辉，女，1975年生，博士，副教授，硕士生导师，主要从事故障检测与诊断工作。

静) (

2016-06-07)

161221