Moran’s I指数与DEM网格大小关系的研究

郤建军，李新通

（福建师范大学 地理科学学院，福建 福州 350007）

Moran’s I指数与DEM网格大小关系的研究

郤建军，李新通*

（福建师范大学 地理科学学院，福建 福州 350007）

数字高程模型（Digital Elevation Model，简称DEM）作为真实地形的一种数字化模拟，网格间存在着某种空间自相关性.Moran’s I是一种常见的空间自相关程度量化指标.为了研究Moran’s I与DEM网格大小之间的关系，文章在分辨率为30 m×30 m的DEM上随机选取了35个采样点.又以每个采样点为中心，选取n×n（n=3，5，7，…，25）大小的DEM网格，计算并记录对应于每个网格的Moran’s I指数值，绘出各采样点的Moran’s I指数值随n变化的曲线.研究发现：大多数采样点的Moran’s I曲线呈现出一致的变化趋势；同时发现少数采样点的Moran’s I曲线出现局部的变化异常.对这些异常进行分析后发现，Moran’s I值随n变化的趋势与DEM网格高程值的离散程度（地形）有关.

DEM；Moran’s I指数；网格；空间自相关

Tobler W R[1]在1979年指出地理空间存在相关性，并在此基础上提出了地理学第一定律：地理事物总在不同程度上互相联系与制约，相距较近事物之间的影响通常大于相距较远事物之间的影响.地理事物或属性在空间分布上互为相关，存在集聚、随机、规则等几种分布.要了解地理事物分布、发展、变化的规律，就要考虑它们之间存在的空间相关性.空间自相关是空间统计学的重要组成部分，被广泛地应用在各种研究中.Cai X M和Wang D B[2]在水文流域地形特征值的空间自相关研究中，使用全局Mo⁃ ran’s I表示具体网格邻域内的空间自相关.以某个网格为中心，选取n×n（n取从3开始的奇数）大小的网格.依次计算10个流域地形特征值的Moran’s I，记录并绘出Moran’s I随邻域增大而变化的曲线图. Pogson M等人[3]引入一个gI/nI（n、g分别是聚合前、后的网格大小，I是Moran’s I值）因素，反映空间自相关性对空间数据不确定性的影响.该文章利用不同的栅格数据测试他们提出的公式的正确性.研究表明数据的空间自相关性会对空间分辨率引起的数据不确定性造成一定的影响.谷建立[4]等人通过计算各土地类型的全局Moran’s I研究谷城县县域整体的空间自相关性.对具体土地类型的Moran散点图分布和局部关联局域指标分布进行了解读.随后，基于DEM五个地形因子的统计数据对谷城县的土地利用自相关格局进行了剖析.张松林[5]等人研究了局部空间自相关指标Moran’s I和G系数两种方法之间的差异.首先随机生成一个规则网格模拟地震带，网格属性为震级，使用固定大小的区域从规则网格的一角向中心移动，探测低值与高值集聚情况，并对两种方法的结果进行了比较分析.陈彦光[6]简化了空间自相关分析过程，论述了计算Moran’s I指数的三种途径.最后，针对河南省鹤壁市人口进行了全局Mo⁃ran’s I、局部LISA、Moran散点图空间自相关分析.结合鹤壁市实际情况对Moran散点图结果进行了详细的分析.Zhu D和Dong Y F[7]根据黄土丘陵沟壑区的DEM数据，以局部Moran’s I量化DEM网格间的空间自相关，通过设置阈值来提取DEM的地形特征点，基于特征点构建不规则三角网，达到简化生成DEM的效果.

在多数研究中，DEM作为一种数据，Moran’s I作为一种量化空间自相关的方法被用在各种案例研究中.本文以DEM为研究对象，以Moran’s I为指标研究DEM的空间自相关性的变化趋势，更深入地探索DEM网格的空间自相关.研究结果可以对使用DEM的案例（尤其是涉及对空间自相关敏感的研究）起到参考作用.同时，结合本文还可以做一些进一步的研究：比如DEM有多种生成方法，不同方法生成的DEM网格表现在空间自相关变化趋势上是否具有差异性，在具体研究中会对研究结果产生什么样的影响；对于一些特殊的地形，例如断崖，研究DEM空间自相关变化趋势可以将地形异常性表现出来.在本文的研究中，使用Java程序计算DEM网格Mo⁃ran’s I，提升了数据处理的效率.

1 基本理论

1.1 空间权重矩阵

要揭示地理事物之间的关系，首先需要定义地理事物之间的邻接关系.空间权重矩阵是空间相邻关系的主要表现方式.与空间位置属性有关的、重要的空间概念有距离、邻接、交互、近邻.建立空间权重矩阵的关键在于空间位置的定义.空间权重矩阵主要有以下几种：左右相邻权重矩阵、上下相邻权重矩阵、Queen（后步）权重矩阵、Rook（车步）权重矩阵、K最近点权重矩阵、基于距离权重矩阵、阈值权重矩阵、Dacey权重矩阵、Cliff-Ord权重矩阵[8].空间权重矩阵的选择直接关系到空间自相关计算结果，所以一些学者建议采用与所研究的特定现象有更直接关系的权重矩阵[9].

空间权重矩阵用一个二维矩阵来表示，基本形式如下：

DEM网格空间邻接有两种：基于距离邻接和基于网格邻接[5].基于距离邻接是指网格A与网格B距离小于规定的距离阈值时权重为1，否则权重为0；基于网格邻接是指根据网格之间的邻接情况，相邻权重为1，否则权重为0.其中常用的有Rook空间权重矩阵、Queen空间权重矩阵.Rook空间权重矩阵易于理解且计算过程较为简单，本文采用的是Rook空间权重矩阵，步长为1.Rook空间权重矩阵的定义为：中心网格与其他网格是否有公共边，有公共边，权重为1，否则权重为0.

1.2 Moran’s I指数

量化空间自相关的指标主要有Moran’s I指数、Geary’s C.本文采用Moran’s I指数来计算DEM的空间自相关性.Moran’s I指数包括全局Moran’s I指数、局部Moran’s I指数.全局Moran’s I指数的计算公式为：

其中，xi是要素i的属性，n为要素的总数，i、j代表不同的要素，wij是要素i和j之间的空间权重.是对应属性的平均值，S2表示所有要素的方差：

全局Moran’s I取值范围为[-1，1].当I大于0时，表示区域内地理事物存在空间正相关；当I小于0时，表示区域内地理事物相对离散；当I接近0时，则表明区域内地理事物不存在空间自相关性，呈随机分布[10-11].

从全局Moran’s I的计算过程来看，所有局部贡献值之和除以全部连接数∑∑wij就是全局Mo⁃ran’s I.其中，每个局部贡献值为：

这些单个的要素Ii称为局部空间关联指标（Local In⁃dicators of Spatial Association，简称LISA），可以用于制图和显著性检验，以提供关于研究区内聚集格局的信息.

1.3 Moran散点图

Moran散点图也是一种局部空间自相关分析方法.能够具体区分区域单元和其邻接单元间的4种空间分布形式[12]，包括High-High、Low-High、Low-Low、High-Low.四个类型区对应Moran散点图的四个象限，每个象限所代表的含义如下[6]：

1）第一象限：为HH区域，即自身为高观测值的点或区域且其周围邻居也多是高值的点或区域，观测值之间具有相似性，呈正的空间自相关，这些点或区域之间在实际情况中呈高值集聚的空间关联模式；

2）第二象限：为LH区域，即低观测值的点或区域且被高观测值的点或区域所包围，观测值之间具有异质性，呈负的空间自相关，这些点或区域之间在实际情况中呈离散分布的空间关联模式；

3）第三象限：为LL区域，即低观测值的点或区域且被同为低观测值的点或区域所包围，观测值之间具有相似性，呈正的空间自相关，这些点或区域之间在实际情况中呈低值集聚分布的空间关联模式；

4）第四象限：为HL区域，即高观测值的点或区域且被低观测值的点或区域所包围，观测值之间具有异质性，呈负的空间自相关，这些点或区域之间在实际情况中呈离散分布的空间关联模式.

2 结果及分析

2.1 方法及结果

DEM矩阵的内容为以高程为属性值的栅格数据.本文目的是探究DEM网格大小对其网格间空间自相关性的影响，在一个空间分辨率为30 m*30 m的DEM中随机选取35个点，以每个点为中心又分别选取3*3、5*5、7*7、9*9、11*11、13*13、15*15、17*17、19*19、21*21、23*23、25*25共12个大小递增的DEM网格.图1是在ArcGIS 10.1中加载显示的样本点位置分布图（35个样本点是在ArcGIS中随机生成的），文章使用的DEM是山地地形，高程范围在438-4361 m之间.

在ArcGIS10.1中将每个采样点的DEM样本转为ASCII文件（*.txt），然后在Java编写的程序中读取ASCII文件，计算并记录样本网格对应的Moran’s I值.关于空间权重矩阵的具体细节请读者参考文后所附的程序源代码，见附录A.绘出Moran’s I值随n变化的曲线即可得到图2所示的结果.

图1 样本分布Fig.1 The distribution of samples

图2 所有采样点的Moran’s I指数变化曲线Fig.2 Moran’s I Index change curve of sample points

接下来，利用Geoda软件对所有的DEM样本进行显著性检验.图3为样本点15的3*3网格和25*25网格显著性检验结果.容易看到，这两种网格表现出一致的显著性规律：3*3网格出现了Low-Low的集聚，对应的区域出现了较高的显著性；随着DEM网格的扩大，25*25网格出现High-High、Low-Low集聚现象，相应的显著性更加明显.这些规律具体表现是：图2的全局Moran’s I曲线呈上升态势.

图3 点15的3*3、25*25网格的LISA集聚图及对应的LISA显著性图Fig.3 LISA cluster map and LISA significance map of grids 3*3 and 25*25 of point 15

2.2 结果分析

分析图2可以发现以下两个显著的规律：一、几乎所有曲线都表现出一致的变化趋势，即随着DEM网格的逐渐增大，Moran’s I数值逐渐增大，Moran’s I数值增长率逐渐减小；二、大多数样本点的3*3网格的Moran’s I值都在0.5左右，这是较高的小范围集聚性的表现.

同时，有少数样本点的Moran’s I曲线出现两种类型的异常.一、曲线走势异常，即整个Moran’s I曲线的走势存在异常，见图4.具体而言：随着DEM网格大小（n）的增加，在13-21区间内，样本点24的Moran’s I曲线呈现下降走势；在7-11、17-21两个区间内，样本点34的Moran’s I曲线也呈现出下降走势.二、曲线初始值异常：Moran’s I曲线的初始值偏小.如图5，对于最小的DEM网格（3*3），各异常样本点的Moran’s I值都小于0.3，小于正常样本点的相应值.

是什么原因导致这两种异常的发生？这些异常表现在DEM上又会是什么地形？本文通过计算DEM网格的方差来分析这个问题.这是因为：Mo⁃ran’s I的计算公式表明，DEM相邻网格之间的高程值的差值会直接影响Moran’s I数值，即，DEM相邻网格之间的高程值的差异影响它们的空间自相关性的高低.本文计算3*3和25*25两种DEM网格的方差.选择3*3网格的主要原因是：Moran’s I曲线的初始值对应于3*3的网格；选择25*25网格的主要原因是：通过计算结果来查看整个DEM网格的高程值的离散程度.两种尺寸DEM网格的方差从不同的角度说明Moran’s I曲线的异常.表1为35个样本点的3*3和25*25两种网格高程方差的计算结果.

图4和图5一共展示了7个异常采样点的Mo⁃ran’s I曲线.从表1可以看出，7个异常采样点的3*3网格方差值都较小（主要集中在0.00-20.00这一范围之内），远小于大部分正常采样点的对应值.这说明，对于3*3的DEM网格，所有异常点高程值都集中在某一个值左右.异常采样点9、24、34和35的25* 25网格方差分别为781.76、263.32、882.42和783.95，小于其他采样点的对应值；异常采样点22和26的25*25网格方差分别为1983.22和2544.05，同样小于大部分的正常采样点对应的值.

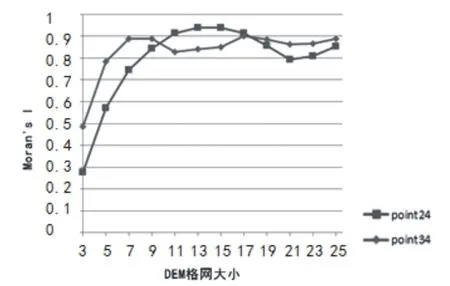
图4 曲线走势异常Fig.4The abnormal of curve trend

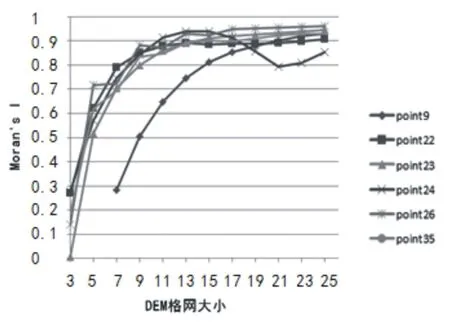
图5 曲线初始值异常Fig.5 The initial values of the abnormal curves

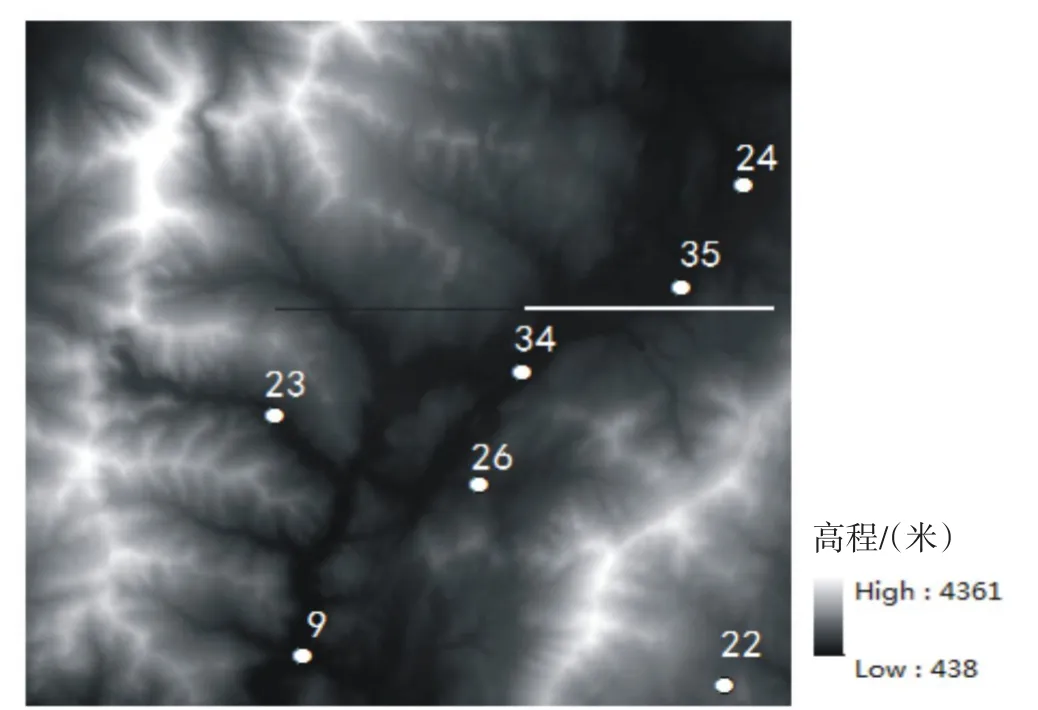
图6 异常点在整个DEM上的位置Fig.6 The distribution of abnormal sample points in DEM

表13 *3和25*25网格的高程方差值（单位：m2）Tab.1The elevation variances of 3*3 and 5*5 DEM’s grids（unit:m2）

结合本文研究区域的DEM高程图（见图6）和DEM坡度图（见图7），查看这些异常采样点的位置分布可知，异常采样点都位于地势相对平坦之处，其中采样点9、22、23、24、34、35位于坡度范围在0-17的位置，采样点26处于坡度范围在18-34的位置.结合7个异常采样点的3*3和25*25网格方差及其高程位置分布图、坡度位置分布图，可以推测，两种Mo⁃ran’s I曲线异常都与采样点所处位置的坡度有关，因为山谷的地势都较为平坦，而这些采样点大多分布在山谷中.（注：图6是对原DEM进行了高程分布渲染操作所得，图7是对原DEM进行了求取坡度操作所得.两幅图的操作都是在ArcGIS 10.1中进行的）.

接下来，通过Moran散点图分析异常采样点与正常采样点之间的区别.异常采样点9以及正常采样点1的25*25 DEM网格的散点图对比见图8和图9.空间自相关的散点与趋势线匹配的效果越好，则自相关性越强[6].从这两幅图的散点分布与直线匹配的情况看，采样点的25*25 DEM网格空间自相关性较高，这也印证了图2中Moran’s I曲线分布.从Mo⁃ran散点图还可以看出，在正常采样点的25*25 DEM网格中，HH、LL区域分布更为均衡，异常采样点则相对集聚.DEM高程值的变化呈现有序递增或递减趋势，没有出现High-Low、Low-High两种情况，相应地，无论是在异常采样点还是正常采样点的散点图中，散点的分布都没有出现在二、四象限.

3 结论与不足

DEM是一种真实地形的数字高程表现形式，一般情况下，DEM矩阵网格之间存在正的空间自相关；空间自相关量化指数Moran’s I同DEM网格大小之间存在关联性：DEM中以一点为中心逐渐向外延伸，随着DEM网格范围的扩大，空间集聚现象逐渐明显，Moran’s I值逐渐增大，Moran’s I值增长率逐渐减小，在DEM网格达到一定范围后，Moran’s I值趋于稳定；Moran’s I值随DEM网格的变化趋势同DEM网格高程值的分布（地形）有关；DEM的空间分辨率的大小决定着真实地形中细节的缺失与否，所以DEM空间分辨率的不同会影响Moran’s I的值.

从本文分析结果来看，异常采样点都出现在地势较为平坦，坡度较小的位置.但是并不是所有位于平坦地势的采样点都表现出异常.从表2中可以看出，正常采样点8、10、13、18、20、29、31的3*3和25*25网格方差都较小，但是这些采样点的Moran’s I曲线没有出现文中提到的两种异常.进一步的分析将在别的研究中进行.

图7 异常点在坡度图上的位置分布Fig.7 The distribution of abnormal sample points in slope DEM

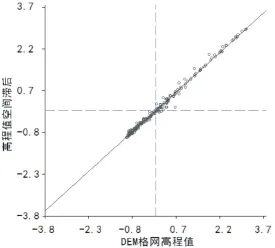
图8 采样点9的散点图分布Fig.8 The scatter diagram of sample point 9

图9 采样点1的散点图分布Fig.9 The scatter diagram of sample point 1

[1]Tobler W R.A computer movie simulating urban growth in the Detroit region[J].Economic geography，1970，46（2）：234-240.

[2]Cai X，Wang D.Spatial autocorrelation of topographic in⁃dex in catchments[J].Journal of Hydrology，2006，328（3）：581-591.

[3]Pogson M，Smith P.Effect of spatial data resolution on un⁃certainty[J].Environmental Modelling&Software，2015，63：87-96.

[4]谷建立，张海涛，陈家赢，等.基于DEM的县域土地利用空间自相关格局分析[J].农业工程学报，2012，28（23）：216-224.

[5]张松林，张昆.空间自相关局部指标Moran指数和G系数研究[J].大地测量与地球动力学，2007，27（3）：31-34.

[6]陈彦光.基于Moran统计量的空间自相关理论发展和方法改进[J].地理研究，2009，28（6）：1449-1463.

[7]Zhu D，Dong Y.Terrain simplification from grid DEMs based on spatial autocorrelation[C]//2013 21st International Conference on Geoinformatics.IEEE，2013：1-5.

[8]徐彬.空间权重矩阵对Moran’s I指数影响的模拟分析[D].南京：南京师范大学，2007.

[9]刘旭华，王劲峰.空间权重矩阵的生成方法分析与实验[ J].地球信息科学，2002，4（2）：38-44.

[10]吴孟泉，赵玉.中国奥运奖牌空间分布区域性差异的Moran’s I指数分析研究[J].中国体育科技，2012（5）：3-9.

[11]田力，张晓盼，袁艳斌.规则网格系统全局Moran指数计算的改进方法[J].测绘科学，2014，39（2）：110-113.

[12]王新成，王斌之，黄建毅.基于空间自相关的水污染空间聚类研究[J].环境工程技术学报，2014，4（4）：293-298.

附录A

车步空间权重矩阵代码

本附录给出空间权重矩阵的核心代码块，详细的介绍见正文第2.1节.

其中，DEM网格的高程值存放在一个二维数组array[row][column]中，row表示行索引值，column表示列索引值.从代码中可以看到有4个if判断语块，通过控制row、column的值，分别是对应中心网格同上、下、左、右网格的判断.

责任编辑：吴兴华

Study of the Relationship Between the Moran’s I Index and the DEM’s Grid Size

XI Jianjun，LI Xintong*
（School of Geography，Fujian Normal University，Fuzhou350007，China）

Digital Elevation Model（DEM）is a digital model of realistic terrain,and there exists spatial auto-correlation among DEM’s grids.The Moran’s I is a quantized index used to measure the spatial auto-correlation.To explore the rela⁃tionship between the Moran’s I index and the size of DEM’s grids,we compute and record the corresponding Moran’s I val⁃ues by selecting 35 samples in the DEM with a resolution of 30 m×30 m randomly and selectingn×n（n=3，5，7，…，25）DEM’s grids centering on each sample point.Finally,we plot the Moran’s I curves varying along withnfor all sample points.The results show that most Moran’s I curves have the same variation trend except for a few curves which have abnor⁃mal behaviors in somen-intervals.By analyzing these abnormal phenomena,we find that the variation trend of a Moran’s I curve along withnis related to the elevation dispersion degree of the corresponding DEM’s grids.

DEM；Moran’s I index；grid；spatial auto-correlation

P 282

：A

：1674-4942（2016）004-0418-07

10.12051/j.issn.1674-4942.2016.04.014

2016-08-28

*通讯作者