基于Logistic回归判别法对大学生挂科的预测
韦新星
(河池学院 数学与统计学院,广西 宜州 546300)
基于Logistic回归判别法对大学生挂科的预测
韦新星
(河池学院 数学与统计学院,广西 宜州 546300)
随着大学生考试挂科现象日益凸显,如何防预大学生挂科已成为高校教育面临的热点问题.文章将Logistic回归分析与判别分析相结合,对大学生挂科的预测问题进行研究.具体实例表明,运用Logistic回归判别法能很好地对大学生考试是否挂科进行预测,从而有利于学校及学生自身采取相应的措施来防止挂科的发生.
大学生挂科;Logistic回归判别法;预测
随着我国高校的不断扩招,我国的高等教育正处于由精英教育转向大众化教育的阶段,这使得众多求学者拥有了享受高等教育的机会.但是,高校扩招也不可避免地为教育质量的提高带来一些新的问题和挑战[1].尤其是大学生挂科方面的问题日益凸显[2].
挂科,即考试不及格.大学生的挂科会造成诸多方面的影响.对学校而言,普遍的学生挂科现象会损害学校的声誉,阻碍高校的发展;对学生而言,挂科不仅会影响其奖助学金、保研等资格的获取,还会影响其学位的获取及能否顺利毕业,甚至会对其心理健康及日常生活产生影响.
截止目前,已有不少学者对大学生的挂科现象进行了研究.张丽华等[2]在对内蒙古工业大学2007级理工科学生的数学考试成绩进行统计分析后发现:高考成绩与性别对该校学生数学挂科的影响较大,学生评教对其也有一定影响,而生源地与学生数学挂科则没有影响.李丹花[3]指出,影响大学生挂科的原因有:一是学习目标不明确;二是沉迷于网络;三是打工分散学习精力;四是为情所困,迷失自我.章瑜[4]在对大学生挂科影响因素的研究中指出:学生课余时间不知道做什么、课上没有归属感是学生挂科的主要原因.罗晨辉[5]指出:物质和精神诱惑、网络、恋爱、目标不明确、思想放松等因素是造成大学生挂科的主要原因.高朋敏[6]从环境变化、目标缺失等方面揭示大学生的挂科原因.黎安康[7]也对影响大学生挂科的因素进行研究.综合分析前人的研究,不难发现大多数的这些研究结论都是通过定性分析或初步的定量分析得到的.
为此,本文在前人研究的基础上,针对所收集到的数据,主要从定量分析的角度出发,尝试将Logistic回归分析与判别分析相结合(简称:Logistic回归判别法),对大学生挂科的预测问题进行研究.
1 Logistic回归判别法简介
对于响应变量y,令y取值1表示事件发生,取值0表示事件不发生,即响应变量y为二分类变量.在n个自变量x1,x2,…,xn的作用下,记事件发生的概率为P(y |x1,x2,…,xn)=p,则Logistic回归模型为[8-9]:

其中βi为Logistic回归模型的系数,β0为回归常数.于是,事件不发生的概率为:

显然,(1)式是一个非线性回归模型,对(1)式作logit变换,则得到Logistic回归模型的线性形式:


判别分析[9]是判别样品所属类型的一种统计方法,它是在已知观测对象的分类结果和若干表明观测对象特征变量值的情况下,通过建立判别函数来判别未知分类对象的归属问题的一种方法.
Logistic回归判别法则是Logistic回归分析和判别分析的结合.运用Logistic回归进行判别分析的基本原理是:用Logistic回归方程计算待判样品属于各类别的概率,当预测概率大于0.5时,就判定该事件发生,否则就判定其不发生[10].
2 大学生挂科实例分析
本节从定量分析的角度,运用Logistic回归判别法对大学生挂科的预测问题进行研究.本实例中的原始数据来自对某高校在校大学生挂科情况的调查问卷.其中y为因变量,10个自变量x1,x2,…,x10分别表示民族、籍贯、性别、年级、专业、是否处于恋爱状态、是否参加兼职工作、是否没有认真学习复习、上课是否经常玩手机、学习上是否不懂就问.具体的变量取值及其对应含义见表1.

表1 变量取值及其对应含义Tab.1Variable values and their corresponding meanings
剔除掉无效问卷后,最终得到300份有效问卷.为检验模型的有效性和模型对问题预测的准确性,随机抽取其中的250份作为训练集,而把剩余的50份作为测试集.
2.1 模型的建立
接下来,运用Logistic回归判别法对训练集进行处理.首先将作为训练集的250份数据导入SPSS软件中,通过“分析—回归—二元Logistic回归”,可得到Logistic回归方程,最后根据Logistic回归方程计算待判别学生属于“挂科”类还是“不挂科”类:当预测概率p大于0.5时,就判定该事件发生,即学生将挂科;否则就判定该事件不发生,即学生不挂科.
首先,进行模型系数的显著性检验.原假设和备择假设分别为:
H0:模型系数对因变量没有显著影响;
H1:模型系数对因变量有显著影响.
具体得到的结果见表2.在表2中,Chi-square表示卡方值,df表示自由度,Sig.则代表显著性检验的P值,通常将其与α进行比较,α常取0.05.而检验的P值是指在原假设成立的前提下,检验统计量等于这个实现值或更极端情况的概率.因此,若该值小于0.05,则表明小概率事件发生,于是拒绝原假设H0[11-12].由表2可知,模型系数的卡方值为69.328,自由度为4,而Sig.值为0.由于自由度为4,故查阅卡方分布表[11]可知,卡方临界值为9.488.由于69.328>9.488,且Sig.值为0<0.05,故拒绝原假设H0,即模型系数对因变量是有显著影响的.
其次,对模型整体性的显著性进行检验.原假设和备择假设分别为:
H0:模型的整体效果不显著;
H1:模型的整体效果是显著的.
表3给出的是模型整体性的拟合效果检验情况.在表3中,-2 Log likelihood为(-2)倍对数似然函数的值,通常要求NagelkerkeR2的值在0.3以上.由于257.381>卡方临界值9.488,所以拒绝原假设H0,即模型的整体效果是显著的.

表2 模型系数的综合检验Tab.2 Comprehensive test of model coefficients
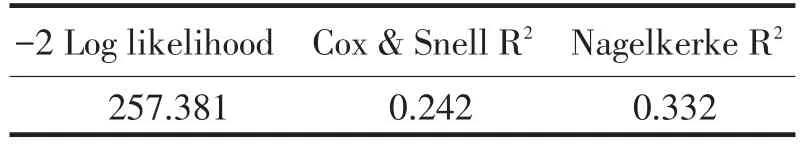
表3 模型汇总Tab.3Summary of models
接下来,对模型系数进行筛选.经过Logistic回归,从10个可能影响挂科的因素中筛选出了4个,分别为性别、是否没有认真学习复习、上课是否经常玩手机、学习上是否不懂就问,而其余变量对挂科的影响过小,模型系数接近于0,故没有筛选出来.表4是变量筛选的结果.

表4 模型系数Tab.4The Coefficients of Model
由表4可知:
①各变量回归系数βi(i=3,8,9,10)的Sig.值均小于0.05,再次表明各变量系数对因变量的影响是显著的.
②y与x3、x10呈负相关,而与x8、x9呈正相关.表明在其它因素不变的情况下,女生及不懂就问的学生比较偏向于不挂科;相反的,没有认真学习复习、上课经常玩手机的学生则更易挂科.而这与实际情况正好相符.
③结合公式(1),可得到大学生挂科情况的Logistic回归模型:

于是,通过Logistic回归方程(3)计算待判别学生的概率值,根据所得预测概率与0.5的关系,便可判定该学生属于挂科一类还是不挂科一类.
2.2 模型的检验
为检验所得模型的优劣,需要进行回代检验和预测检验[13].

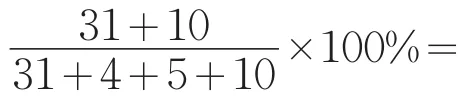

表5 回代检验结果Tab.5 The results of backing test

表6 预测检验结果Tab.6 The results of forecast test
2.3 模型的应用
假定需要对甲、乙两名学生进行预测,即需要预先判定其各自属于挂科一类还是不挂科一类,以便日后采取相应的措施对其进行防治.只需把相应的变量值代入(3)式,计算出待判学生的概率,并根据所得预测概率与0.5的关系,便可判定该学生是属于挂科一类还是不挂科一类.
例如,假设甲是不太认真学习复习、上课比较喜欢玩手机、学习上不懂的地方从来不问的女生,乙是有点认真学习复习、上课非常喜欢玩手机、学习上不懂的地方从来不问的男生,则利用公式(3),可算出甲属于挂科类的概率为0.788,而乙属于挂科类的概率为0.917,甲乙二人的概率均大于0.5,于是可判定该二人均属于挂科一类.此外,由于0.917>0.788,故需更关注乙的学习情况,以便及时采取适当措施防止其挂科的发生.
3 结论
本文将Logistic回归分析与判别分析相结合,运用Logistic回归判别法来处理大学生挂科的预测问题,得到了大学生挂科情况的Logistic回归模型.回代检验和预测检验表明该模型能较好地根据学生的一些特征,来预测学生的挂科情况发生概率,进而有利于学校及学生自身采取相应的措施来防止挂科的发生.值得一提的是,本文的结论是基于从某高校收集到的数据而言的,所以具有一定的针对性和局限性.然而,当样本容量足够大、涉及面足够广时,本文的研究仍具有一定的参考价值和指导价值.
[1]文菊,姚利民.高等教育大众化背景下提高高校教学质量的对策初探[J].高等教育研究学报,2005,28(4):87-90.
[2]张丽华,戴学芳,刘志强,等.基于Logistic模型的大学数学挂科原因实证分析[J].内蒙古师范大学学报,2014,27(9):135-138.
[3]李丹花.高校大学生挂科现象原因与对策研究[J].技术与市场,2015,22(10):168-169.
[4]章瑜.大学生挂科的对策研究[J].中国科教创新导刊,2009(23):14.
[5]罗晨辉.对大学生挂科现象的思考[J].中国校外教育,2010(18):37.
[6]高朋敏,齐艳萍.新形势下高校学生“挂科”原因初探及应对措施[J].社科纵横,2016,31(10):170-173.
[7]黎安康,梁永宏.日趋严重的大学生“挂科”现象原因探析[J].长春教育学院学报,2014,30(2):149-150.
[8]杜强,贾丽艳.SPSS统计分析从入门到精通[M].北京:人民邮电出版社,2011.
[9]李静萍,谢邦昌.多元统计分析方法与应用[M].北京:中国人民大学出版社,2008.
[10]马逢时,吴诚鸥,蔡霞.基于MINITAB的现代实用统计[M].北京:中国人民大学出版社,2009.
[11]叶慈南,曹伟丽.应用数理统计[M].北京:机械工业出版社,2013.
[12]吴喜之.统计学:从数据到结论[M].北京:中国统计出版社,2005.
[13]李春红,韦新星,刘胜臣.Cox模型在电信客户流失原因分析中的研究[J].海南师范大学学报,2013,26(4):368-371.
责任编辑:吴兴华
Prediction of College Students’Failing Exams Based on the Logistic Regression and Discriminant Method
WEI Xinxing
(School of Mathematics and Statistics,Hechi University,Yizhou546300,China)
Since college students’failure in exams is becoming more and more popular,how to solve the problem has be⁃come a hot topic in higher education.This article studies the prediction of students’failure in exams by combining the Logis⁃tic regression analysis and discriminant analysis.The specific examples show that the Logistic regression and discriminant method can make the prediction very well,and is helpful for schools and students to take steps beforehand.
college students’failing the exam;Logistic regression and discriminant method;prediction
O 212.1
:A
:1674-4942(2016)04-0379-04
10.12051/j.issn.1674-4942.2016.04.005
2016-09-03
广西高校中青年教师基础能力提升项目(KY2016LX279);广西大学生创新创业训练计划项目(201610605054);河池学院硕士专业学位建设基金课题(2016YT004)

