一类分段非线性映射的混沌边界分析
许宏飞,李群宏,宁 敏,商梦媛
(广西大学 数学与信息科学学院,广西 南宁 530004)
一类分段非线性映射的混沌边界分析
许宏飞,李群宏*,宁 敏,商梦媛
(广西大学 数学与信息科学学院,广西 南宁 530004)
文章研究了一类具有非线性分支的分段映射的动力学行为.该模型可能应用到物理科学、工程和医学方面,也有助于一些经济模型的研究.以μ为分岔参数得到系统的分岔图,发现在系统的不变吸引区间内,周期轨道的每个周期点都有一定的存在范围,这造成分岔结构中出现迭代禁区现象.通过理论推导确定了周期轨道周期点的存在范围和禁区边界,进一步通过禁区边界得到了混沌区域与周期n轨道区域的边界的表达式,应用Lyapunov指数对分析结果进行了验证.
分岔;禁区边界;混沌边界;分段非线性不连续映射;Lyapunov指数
近些年,分段不连续映射动力系统在物理科学、工程、经济和医学等方面已经有了大量的研究[1-8].但以往的研究大多只考虑系统的边界碰撞分岔,对系统的加周期现象和周期叠加现象进行理论分析和研究,对系统出现的混沌边界的研究不多,尤其是对混沌区域与周期性区域边界的研究较少.文献[6]研究了一类具有可变禁区系统的不同类型的加周期分岔现象,发现系统的周期性区域与混沌区域的边界线刚好处于左右边界碰撞分岔同时发生的区域.文献[9]建立了RC开关电路的一维分段映射模型,研究了系统参数变化诱导出的混沌吸引子的崩溃.现在已经证明,鲁棒混沌区接近由包含无数条分岔曲线的加周期结构组成的周期性区域,这些分岔曲线形成加波段现象,这些现象标志着多波段混沌吸引子的发生[10].文献[11]研究了TCP-RED离散反馈系统的周期稳态经过边界碰撞分岔转迁到混沌态的整个过程.文献[12]研究了分段不连续映射模型,利用分岔解释分段不连续映射诱导出的多波段混沌吸引子的结构.文献[13]分析了分段不连续映射系统的整个混沌域的分岔结构,发现系统的鲁棒混沌吸引子嵌在两个不同周期的周期性区域之间,给出了系统混沌吸引子的边界表达形式.文献[14]基于经济领域中的问题建立了一类分段不连续非线性映射模型,并分析了该系统的边界碰撞分岔,给出了混沌区间的范围.文献[15]对如下不连续映射模型
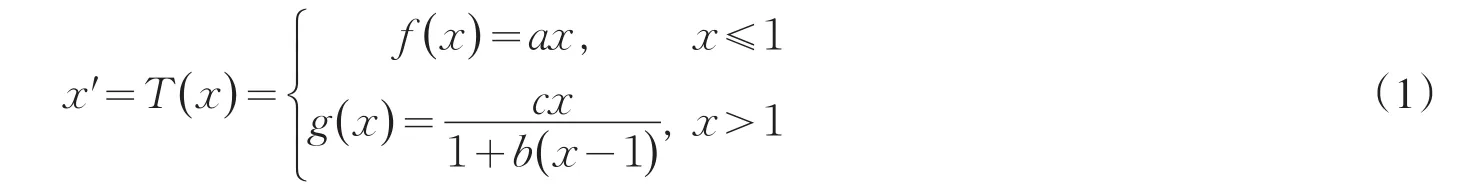
进行了讨论.研究结果表明,系统存在加周期现象和混沌现象.文献[16]将模型(1)的线性分支变为f(x)=ax+μ,主要讨论了常数项对系统边界碰撞分岔的影响,并对系统做了双参数和三参数的分岔分析,但对混沌边界没有作相关研究.
本文主要研究文献[16]中分段非线性映射系统分岔迭代结构的禁区和系统出现的混沌的边界.本文第1节通过理论分析系统的迭代表达式,得到系统的周期轨道中任意周期点的取值范围,从而得到系统迭代点的禁区边界曲线.第2节借助不连续映射的Lyapunov指数和分岔图确定系统混沌区域与周期n轨道区域的边界.在最后一节做出简要的结论.
1 周期点的禁区
本文主要研究的模型为分段非线性映射,即
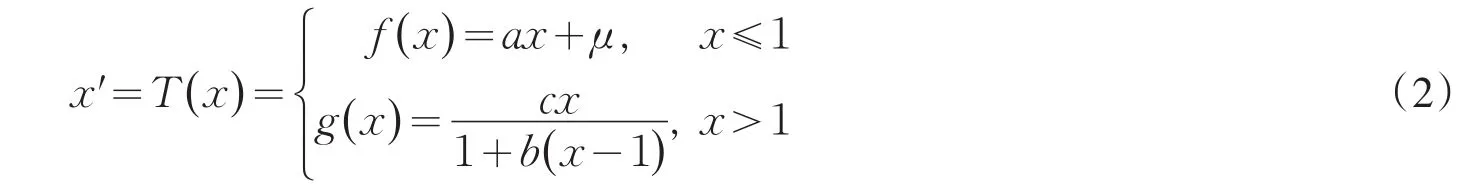
其中a>1,0<b<1,0<c<1,μ>-1.这里的x′代表映射的值,不代表x的导数.当a+μ=c时,系统(2)为连续非线性映射,当a+μ≠c时,系统(2)为不连续非线性映射.记所研究的参数空间为
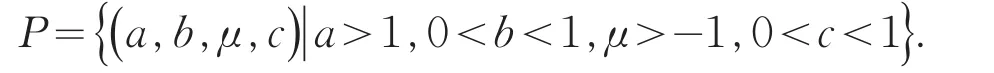
不连续点x=1将状态空间分割为两个区域
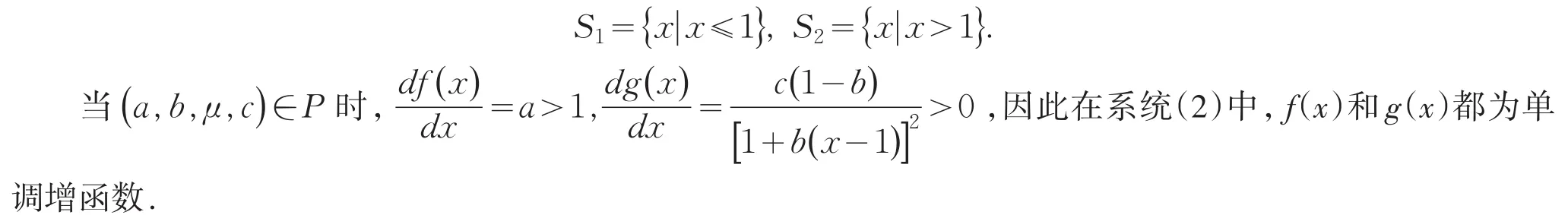
1.1 不动点分析
性质 当(a,b,μ,c)∈P时,系统(2)的迭代点在(-∞,]内随着迭代次数单调递减,在(,1]内随着迭代次数单调递增.
证明 设x0为迭代的初始点,在S1区域内迭代k次,则xk=f(xk-1),(k≥1),经递推可得
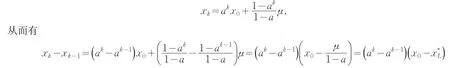
当(a,b,μ,c)∈P时,有a>1,由于为S1区域内容许不动点,所以当x0≤时,xk≤xk-1;当1≥x0>时,xk>xk-1;即系统(2)的迭代点在(-∞,]内单调递减,在(,1]内单调递增.因此,S1区域内的点经过有限次迭代一定会到达S2区域内.
1.2 禁区分析
周期点的禁区表示周期轨道的周期点不存在的区间.若用Rk表示非线性函数g(x)迭代k次,用L表示线性函数(fx)迭代一次,形成的周期k+1解的符号序列记为RkL.


选取参数a=1.6,b=0.1,c=0.8,-0.4≤μ≤1得到全局分岔图.图1为添加了迭代禁区边界线的全局分岔图.观察图1容易得到,在μ>-0.2区域存在周期3轨道区域,周期4轨道区域,且在周期3轨道区域与周期4轨道区域之间夹有周期7轨道区域,也存在更复杂的周期n轨道区域.还观察到在直线x=f(g(1))和直线x=g(f(1))之间没有迭代点,直线x=g(f(g(1)))和直线x=g2(f(1))之间也为空白区域;同时还发现这些禁区边界线将分岔结构分割为若干“长带”.若每一组禁区边界线都相交,即分岔结构的“长带”之间没有空白区域,迭代点铺满整个不变吸引区间,也就是说每一个μ所对应的这组参数,系统(2)有无数个迭代点,这是不可能形成周期轨道的,此时系统(2)应该出现混沌现象.由以上分析可得,系统(2)禁区边界线的交点应该落在周期n轨道区域与混沌区域的边界线上.下一节,通过Lyapunov指数谱来验证这个结论.
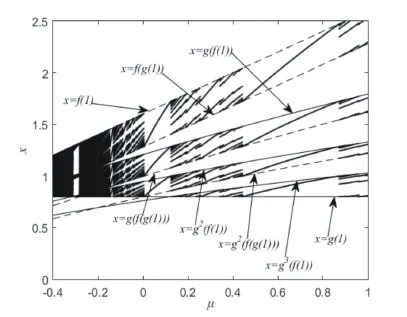
图1 全局分岔图Fig.1 Global bifurcation diagram
2 混沌边界
Lyapunov指数是判别一个动力系统做周期运动还是混沌运动的一个重要物理量.根据系统(2),其Ly⁃apunov指数λ为
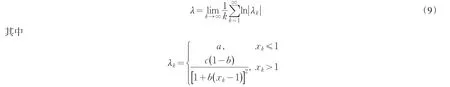
由(9)式可以得到系统(2)的Lyapunov指数图.为了便于比较,我们将两幅图绘制在同一坐标下,见图2(a).
图2(a)是禁区边界曲线与Lyapunov指数图合并图,图中最下方为Lyapunov指数曲线,图2(b)为图2(a)Lyapunov指数图的放大图.由图2(a)知,在直线μ=μ0的左侧,Lyapunov指数大于零,在右侧,Lyapunov指数小于零,因此竖直线μ=μ0即为混沌区域与周期n轨道区域的分界线.图2(a)的虚线由上到下分别是:
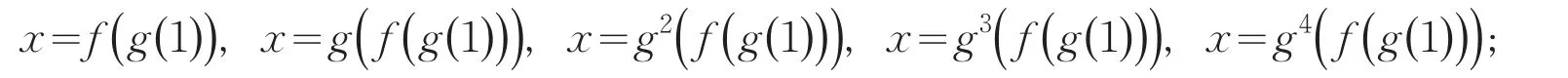
实线由上到下分别是:
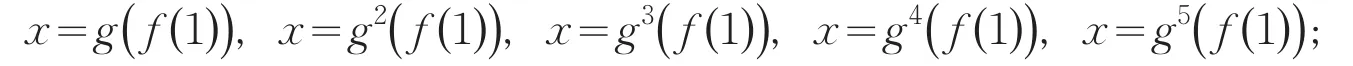
边界线x=f(g(1))与x=g(f(1))相交,x=g(f(g(1)))与x=g2(f(1))相交,等等.经过观察发现每一组禁区边界线gi(f(1))和gi-1(f(g(1))),i=1,2,…,k都相交且交点都落在直线μ=μ0上;因此,禁区边界线的交点可以确定直线μ=μ0.由式(8)可得:
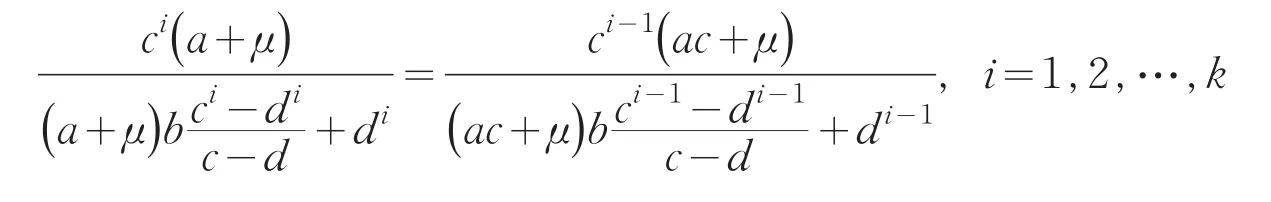
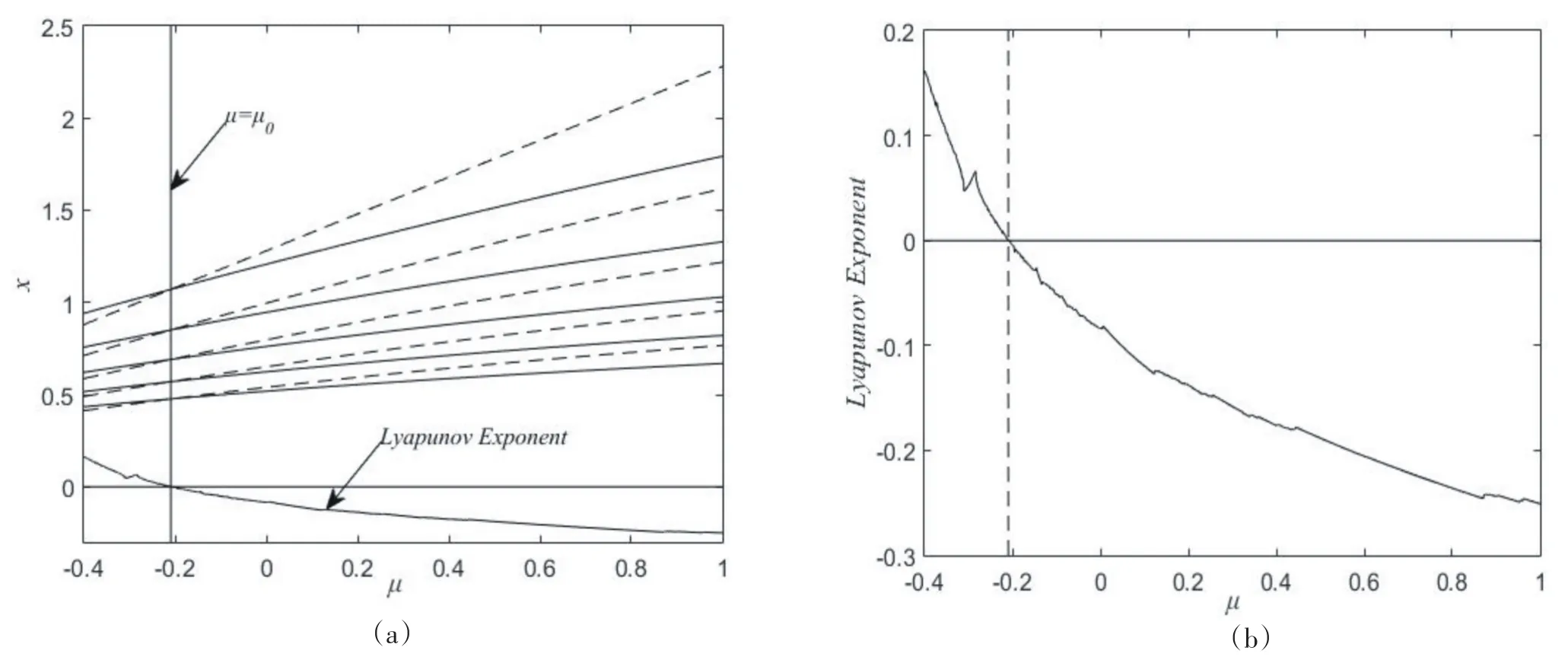
图2 (a)禁区边界曲线与Lyapunov指数图合并图,(b)Lyapunov指数图Fig.2(a)Combination of forbidden boundary curve and Lyapunov exponent diagram;(b)Lyapunov exponent diagram
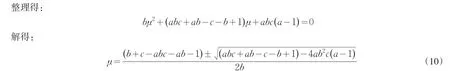
(10)式即为混沌区域与周期n轨道区域的分界线解析式,注意这里计算得到的是两个μ值,具体的选择需要参照做分岔图时μ所取的范围.因为选取的参数为a=1.6,b=0.1,c=0.8,-0.4≤μ≤1,所以图1中混沌区域与周期n轨道区域的边界线为μ=-0.2092.
3 结论
本文针对具有非线性右侧分支的分段一维映射模型(2)展开研究.在系统(2)的不变吸引区间内,讨论了周期轨道各周期点的存在范围.得到了分岔图中分岔结构的迭代禁区的边界线.对禁区边界线进行理论分析发现,分段映射系统的禁区边界线的交点落在混沌区域与周期n轨道区域的分界线上.进而给出了混沌区域边界线的解析表达式.采用Lyapunov指数谱验证了该结论的可靠性.
[1]沙金,包伯成,许建平,等.脉冲序列控制电流断续模式Buck变换器的动力学建模与边界碰撞分岔[J].物理学报,2012,61(12):120501-1-120501-13.
[2]谢帆,杨汝,张波.电流反馈型Buck变换器二维分段光滑系统边界碰撞和分岔研究[J].物理学报,2010,59(12):8393-8406.
[3]戴栋,马西奎,李小峰.一类具有两个边界的分段光滑系统中边界碰撞分岔现象及混沌[J].物理学报,2003,52(11):2729-2736.
[4]Qu Z,Shiferaw Y,Weiss J N.Nonlinear dynamics of cardiac excitation-contraction coupling:an iterated map study[J].Physical Review E,2007,75(1):112-118.
[5]Sushko I,Gardini L.Degenerate bifurcations and border collisions in piecewise smooth 1D and 2D maps[J].International Journal of Bifurcation&Chaos,2010,20(7):2045-2070.
[6]杨科利.一类可变禁区的不连续系统的加周期分岔[J].物理学报,2015,64(12):91-97.
[7]Gardini L,Tramontana F,Avrutin V.Border-collision bifurcations in 1D piecewise-linear maps and LEONOV's approach[J]. International Journal of Bifurcation&Chaos,2011,20(10):3085-3104.
[8]秦志英,李群宏.一类非光滑映射的边界碰撞分岔[J].力学学报,2013,45(1):25-29.
[9]Avrutin V,Clüver M,Mahout V,et al.Bandcount adding structure and collapse of chaotic attractors in a piecewise linear bimodal map[J].Physica D:Nonlinear Phenomena,2015,309:37-56.
[10]Avrutin V,Schanz M,Gardini L.Self-similarity of the bandcount adding structures:Calculation by map replacement[J].Regular &Chaotic Dynamics,2010,15(15):685-703.
[11]杨谈,金跃辉,程时端.TCP-RED离散反馈系统中的边界碰撞分岔及混沌控制[J].Acta Physica Sinica,2009,58(8):5224-5237.
[12]Avrutin V,Schanz M.On the fully developed bandcount adding scenario[J].Nonlinearity,2008,21(5):1077-1103.
[13]Avrutin V,Schanz M,Schenke B.Coexistence of the Bandcount-Adding and Bandcount-Increment Scenarios[J].Discrete Dy⁃namics in Nature&Society,2011,2011:701-716.
[14]Gardini L,Sushko I,Naimzada A K.Growing through chaotic intervals[J].Journal of Economic Theory,2008,143(1):541-557.
[15]Jain P,Banerjee S.Border-collision bifurcations in one-dimensional discontinuous maps[J].International Journal of Bifurcation &Chaos,2011,13(11):3341-3351.
[16]韦丽梅.分段映射的边界碰撞分岔及混沌控制[D].南宁:广西大学,2014.
[17]Bernardo M di,Budd C J,Champneys A R,et al.Piecewise-smooth Dynamical Systems:Theory and Applications[M].London: Springer-Verlag,2008.
责任编辑:吴兴华
Analysis of the Chaotic Boundary in a Class of Piecewise Nonlinear Mapping
XU Hongfei,LI Qunhong*,NING Min,SHANG Mengyuan
(School of Mathematics and Information Sciences,Guangxi University,Nanning530004,China)
In this paper the dynamical behaviors of a class of discontinuous one-dimensional mappings with a nonlinear branch are studied.This kind of models can be used in physical science,engineering,and medical science,and is also help⁃ful to the study of economics models.Takingμas a bifurcation parameter to draw the bifurcation diagram of the system,we find that in the invariant attracting region of the system there is an existence range for each point of the periodic orbit,and it leads to iteration forbidden region appearing in the bifurcation structure.By theoretical derivation,the article determines the existence ranges of the periodic orbits and the boundary of the forbidden region,obtains the boundary expression of the chaot⁃ic region and the period-norbits region by the boundary of the forbidden region,and finally verifies the analytic results by the Lyapunov exponents.
bifurcation;forbidden boundary;chaotic boundary;piecewise nonlinear mapping;Lyapunov exponent
O 317;O 193
:A
:1674-4942(2016)04-0363-06
10.12051/j.issn.1674-4942.2016.04.002
2016-09-17
广西自然科学基金(2013GXNSFAA019017,2014GXNSFBA118024)
*通讯作者

