使用浮标数据验证高频地波雷达反演涌浪频率*

王炜荔， 管长龙， Philippe Forget， 孙　建

(1.中国海洋大学物理海洋实验室, 山东 青岛 266100；

2.土伦大学 CNRS/INSU IRD 地中海海洋研究所(MIO) UM110, 法国 La Garde Cedex 83957；

3.艾克斯-马赛大学 CNRS/INSU IRD MIO UM110, 法国Marseille 13288)



使用浮标数据验证高频地波雷达反演涌浪频率*

王炜荔1,2,3， 管长龙1**， Philippe Forget2,3， 孙建1

(1.中国海洋大学物理海洋实验室, 山东 青岛 266100；

2.土伦大学 CNRS/INSU IRD 地中海海洋研究所(MIO) UM110, 法国 La Garde Cedex 83957；

3.艾克斯-马赛大学 CNRS/INSU IRD MIO UM110, 法国Marseille 13288)

摘要：涌浪在近海海洋环境中起到的重要影响受到了越来越多的关注。高频地波雷达提供了一种准实时观测涌浪的新手段。本文比较了法国Iroise海区2008年2—7月期间的涌浪频率的浮标观测结果和高频雷达反演结果。结果表明，雷达反演涌浪频率与浮标结果总体吻合良好，两种观测方式之间的相关系数为0.92，均方根偏差为0.0045Hz。雷达观测结果大部分集中在2—4月中低频涌浪发生的时期，而对5—7月期间的高频涌浪的观测能力显著降低。

关键词：涌浪频率；高频地波雷达；WERA；浮标

近十年来，涌浪在海洋环境中所起到的重要作用被越来越多地发现，如涌浪与大气边界层的相互作用，非线性波波相互作用等[1-2]。涌浪是由外海风暴产生经过长距离传播进入当地海域的海浪，通常位于当地海浪谱的低频部分。在近海，涌浪波高增加，能量集中破碎，对于当地的海面和海岸生活生产安全造成很大的影响。涌浪信息的获取对于人们的生产生活，研究波浪传播以及波浪之间相互作用等物理过程均具有积极意义。

然而，涌浪预报和研究往往受制于实测海洋资料的不足。目前，对海洋表面进行探测的方式大致可以分为传统观测手段，如锚定浮标，和新发展的卫星探测的方式，它们各自有其独特的观测优势。传统观测方式时间分辨率高、精度高，然而大多是定点观测，实施成本昂贵，获得资料相对较少。高度计和SAR等卫星遥感方式可以一次性获得大范围的海面信息，甚至可以达到较好的观测精度。然而卫星特定的运行轨迹决定了其对海面的观测只能在特定的时刻进行，而且无法对测点提供时间上连续的长时间观测记录。高频地波雷达(HFR)是发射频率在高频波段(3～30MHz)的无线电设备，通常安装在海岸开阔处，以掠射角扫描海面，其可探测海表面范围可达到上百公里。HFR同时具备了能耗低、连续全天候观测、测量区域广、采样频率高、时空分辨率高等优点。使用该技术反演涌浪可以实现涌浪大范围，多数量，低成本的准实时观测。

本文回顾了使用雷达测量涌浪频率的计算方法[3]，并使用2008年2—7月期间的浮标观测数据对由高频地波雷达多普勒回波谱的二阶谱段计算得到的涌浪的频率进行了验证。

1研究背景

HFR的海表面回波产生机制是Bragg共振散射[4]。海面上具有特定波长的表面波可以与入射电磁波发生作用而使得反射电磁波产生位相相关加强。产生共振的海浪是海面上波长为雷达发射电磁波波长一半的“Bragg波”。Bragg波在回波的多普勒谱中造成对称分布的两个显著尖峰，称为一阶谱峰。由一阶谱峰可以反演海流径向流速[5]。近年来，HFR反演海洋表面流的能力得到了比较充分的验证并被广范应用到近海海流矢量场的准实时观测中[6-8]。

由一阶谱的信息不仅可以计算海流，而且同时由Bragg共振关系可以确定海面上的Bragg波频率。但作为随机过程的海面由众多频率波动组成，如果单纯利用一阶谱信息则需要使用雷达在一个很大的发射频率范围进行扫描才能够获得海面上各个频率波浪的信息。在实际应用中，如此大范围电磁波频段的使用以及设备造价等方面的考虑限制了这种方法的发展。但是，海面波浪通过特定的组合形式可以对雷达波产生二级散射，它们的信息存在于雷达多普勒谱的高阶谱段中。因而，研究单一发射频率雷达的回波中高阶多普勒谱中的海浪信息提取方法具有重要意义。

围绕一阶多普勒谱峰的次显著连续谱部分称为二阶谱。二阶谱由海面上特定的波浪组合产生。随机导电海洋表面和其上的电磁波场可以表达为二维傅立叶级数。Hasselmann[9]指出，HFR回波多普勒谱与海浪谱之间的相关性，认为回波多普勒谱可以解释成海浪谱与一个权重函数的乘积。Barrick[10]给出了二阶谱和海浪谱之间的理论积分关系式。然而，二者之间的对应关系非常复杂。目前海浪谱反演大多采用半经验的模型，主要用于计算海面整体有效波高等整体积分参数[11-12]。

Broche[13]指出，对于海浪谱中的长周期波浪，这种对应关系相对简单。Forget等[14]对窄频单一方向涌浪的频率和雷达多普勒频率之间的关系进行了进一步探讨。Lipa等[15]在Barrick理论的基础上给出了涌浪参数的计算公式,并给出了有限的计算案例。涌浪在二阶回波谱中造成4个对应特定多普勒频率的尖峰。它们分别位于2个一阶Bragg峰周围。通过这些涌浪谱峰的位置和幅值可以计算涌浪参数。

2计算方法

雷达波长λ与造成回波散射的Bragg波波长L之间满足关系

λ=2Lcosθ0。

(1)

其中θ0是电磁波束与地面之间夹角。由于HFR以擦地角入射，θ0约为零，式中余弦函数约为1，因此相干条件决定了Bragg波波长约为雷达波长一半，

L=λ/2。

(2)

Bragg波在雷达多普勒谱中造成对称分布的两个尖峰，其谱峰位置频率称为Bragg频率，fB。由Bragg波的相速度V可知Bragg频率大小为

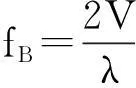
(3)

重力波的相速与波长满足

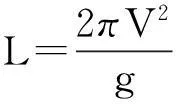
(4)

其中g为重力加速度。结合上面三式得

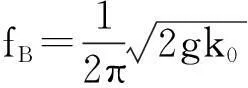
(5)

其中k0为雷达电磁波波数。由此可知，Bragg频率的大小仅由雷达发射频率决定，且与发射频率的均方根成正比。

基于平稳随机导电海表面的一阶散射解，Barrick[5]将相关分析进一步扩展到了移动表面的研究。Barrick[10]给出了在深水情形下，如果不考虑海洋表面流，以每单位面积及单位rad/s带宽的平均散射截面来表示的垂直极化的二阶雷达散射截面

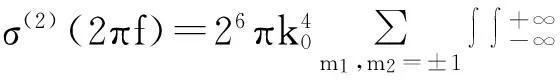
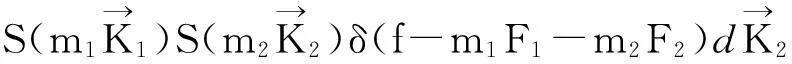
(6)

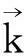
本文的计算基于Lipa等[15]提出的并由Forget[14]进行近似简化的涌浪计算方法。当海面上存在涌浪时，回波多普勒谱中出现4个对应的涌浪谱峰，由左向右依次为f1～f4。由此可以计算涌浪频率Fs和方向θs

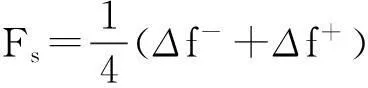
(7)

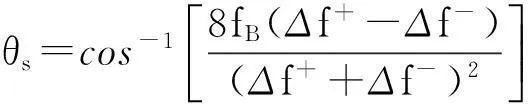
(8)

其中，Δf+和Δf-分别是正、负多普勒谱频段两个涌浪谱峰的多普勒频率差值，即Δf+=f4-f3，Δf-=f2-f1。由于雷达和浮标对波向的观测精度都较低，本文暂不探讨波向的计算结果及对比情形。

风浪被视作随机过程，而涌浪在时间上相对稳定。为突显涌浪特征，本文对雷达数据进行了每小时平均。质量控制和相关技术细节参见Wang等[3]给出的针对该雷达数据库的质量控制和时空平滑处理方法。平滑后的雷达数据径向空间分辨率为6km，角度分辨率为5°，时间分辨率为1h。图1展示了距浮标最近的R1雷达单元所接收信号的多普勒谱样本。由下而上分别是2008年3月2—3日期间的0、12点共4份多普勒谱样本。为了图示方便，由下至上人为逐级增加40dB间距。图中横轴是多普勒频率；竖轴是多普勒谱幅值；虚线代表了±Bragg频率的位置；点线划分出本文认定的二阶连续谱中涌浪谱峰的范围(对应涌浪频率0.045～0.126Hz)。

3研究区域

本文研究区域为法国西海岸以外的Iroise海区，该区域位于大西洋东部，大洋风暴产生的波浪很多经过长距离传输后进入该海域，造成了当地频繁的涌浪事件。雷达数据使用了法国西部布列塔尼地区由SHOM (Service Hydrographique et Océanographique de la Marine) 安装的雷达系统的单站(R1)数据。该系统已被充分验证可以有效进行高时空分辨率的准实时海流观测[16]。雷达为WERA系统，由Gurgel等[17]设计，德国Helzel Messtechnik GmbH制造。其发射频率约为12MHz。接受天线由16根均匀分布的天线组成，总长150m。该系统自2006年开始工作，每20min收集一次数据。空间覆盖范围为11～149km，覆盖面张开角度为120°。图2中大号蓝色圆点标示了雷达站的位置，呈扇形展开的小的蓝色圆点代表了覆盖面上划分的雷达单元，粗黑色曲线为岸线，细黑色曲线标示了30，50，80和100m等深线。

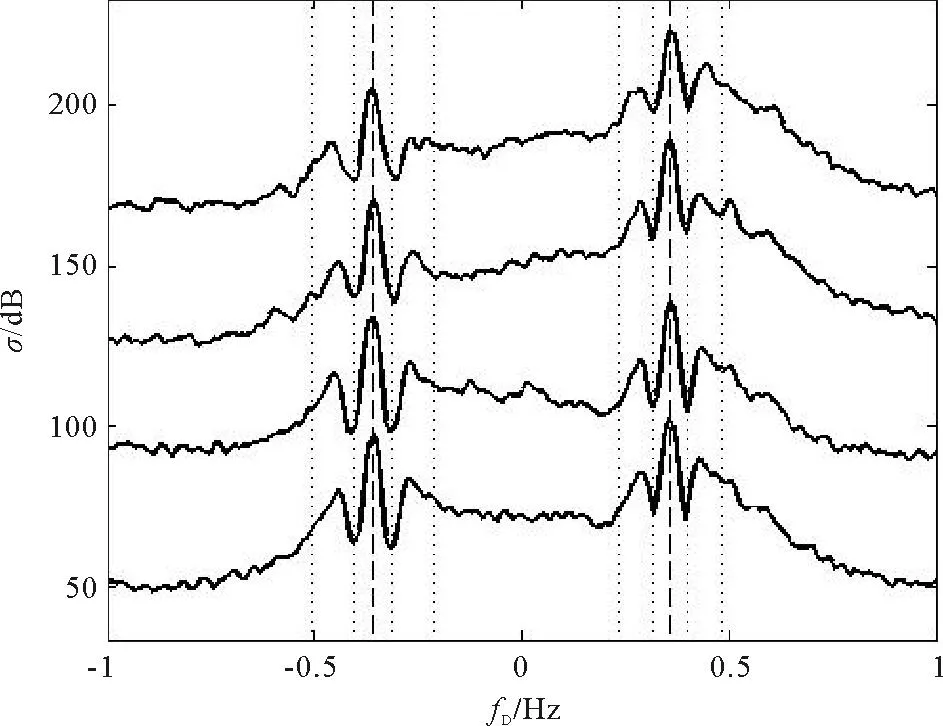
图1　1h平均后的雷达多普勒谱样本

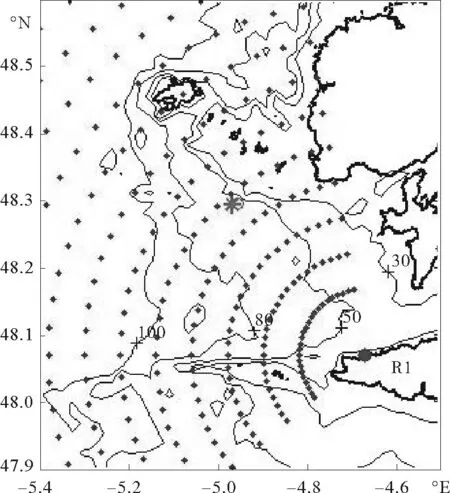
图2　雷达(大号蓝色圆点)和浮标(红色星号)位置示意图

浮标数据来自位于4°58′1″W，48°17′42″N的“Pierres Noires”锚定浮标。图2中红色星号标示出浮标所在位置,当地水深超过50m,浮标数据时长为2008年2—7月。距浮标最近的雷达单元位于距雷达站35km，距中心波束-30°位置处,浮标与该雷达元的直线距离为0.75km,浮标获取的海浪谱为每半小时一次。图3展示了由浮标数据获得的海浪谱的样本,图中红色竖线标示出了本文识别的涌浪谱峰的位置。图3(a)展示的涌浪频率展宽较窄，风浪位于高频部分较为显著;而图3(b)中的涌浪频率幅度较宽，与当地风浪的分界不非常明显。

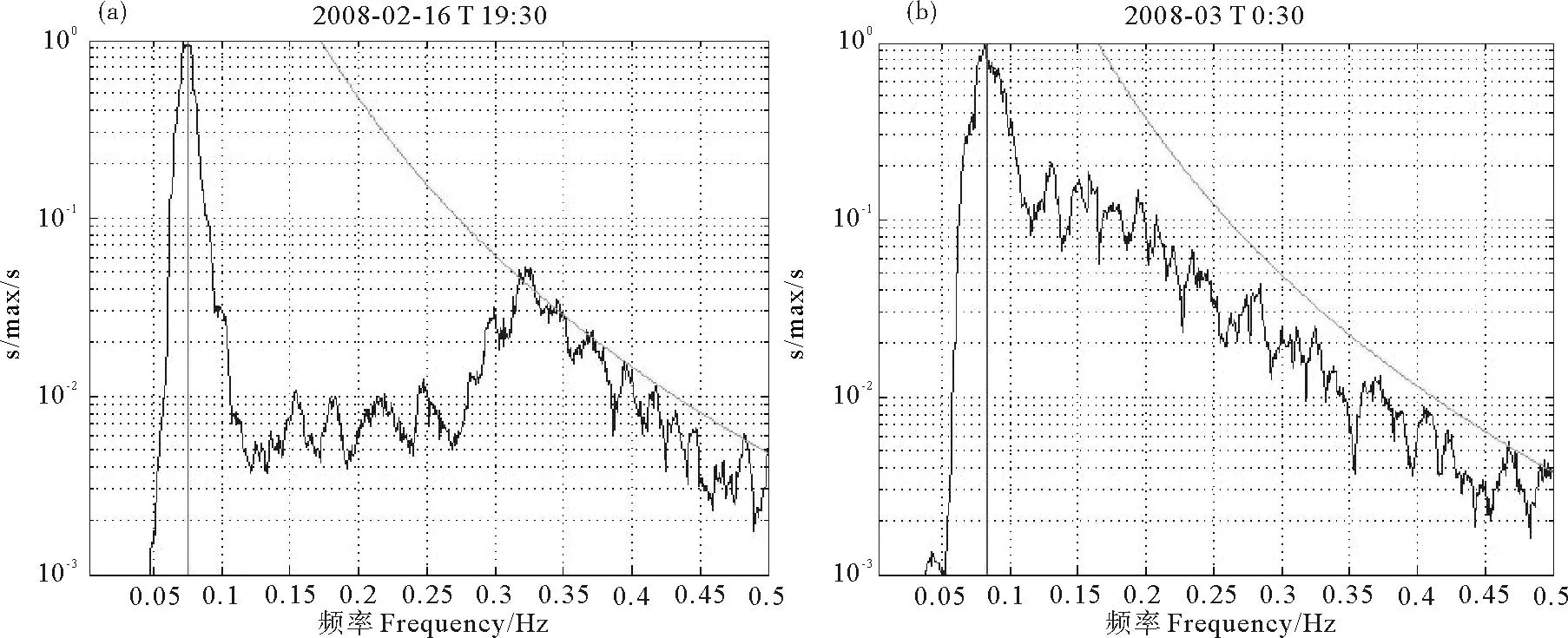
(纵轴坐标中S为谱密度；蓝色曲线为实测海浪功率谱；绿色曲线为采用PM无向谱拟合的参考线；红色直线标示出涌浪谱峰的位置。S in the y-label is the spectral density; Blue curve shows the measured ocean wave spectrum; Green curve shows the fitting curve using PM non-directional model; Red line indicates the identified swell peak.)

图3浮标测得的海面波浪谱样本

Fig.3Samples of ocean wave spectra measured by buoy

4结果和讨论

本文使用距离浮标最近的雷达单元上的涌浪频率计算结果(Fsr)与浮标结果(Fsb)进行比较。2008年2月26日—3月5日期间，雷达反演的涌浪频率(圆圈)与浮标测量结果(星号)对比的时间序列见图4。图中展示时间间隔为每3h一次。图中展出的两种数据对比的时间节点为获取到有效雷达观测的时刻点。由图可见，两种观测结果随时间的变动形态基本一致,这段时间序列包含了3个典型的涌浪事件,每一个涌浪事件对应于在该单元上观察到的涌浪频率准线性上升的过程,这个特点是由波浪传播的频散特性造成的。它们是由同一个远距离风暴中心所产生的涌浪，当远处风暴产生波浪后，低频波浪传播较快而高频波浪传播较慢[18]。浮标和雷达观测都较好地呈现了这3个涌浪事件的频率变化过程。在2月27日凌晨前，和2月28日零点之后，3月5日零点之后等几个时刻二者计算结果相差略大,总体二者吻合较好。

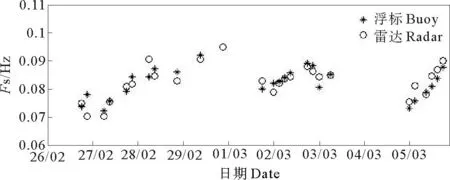
图4　雷达反演涌浪频率与浮标结果对比的

结合浮标数据测得的涌浪有效波高和图4中的频率结果，可以进一步观察频率和波高在这3次涌浪事件过程中的变化和关联(见图5)。由图可以观察到，对于第1次和第3次涌浪事件过程，在定点观测到频率上升的同时，大致伴随着波高的准线性降低，这可以由波浪传播过程中的频散特性来解释。但图中第2次的涌浪事件呈现的频率和波高的关系则略为杂乱。

使用全部浮标数据与雷达结果进行比较的情形见图 6，共统计到478个样本。5个月的时期内大部分观测到的涌浪频率位于0.07～ 0.1 Hz的频率区间。相对于特定频率的浮标测量值，雷达测量结果偏高的情形较少，偏低的情形较多。浮标数据值在0.105Hz左右的2个异常值，均为雷达结果偏低。在样本数较多的中间频率区间，二者吻合比较好，离散程度也较小。在低频频段，2种观测结果吻合也比较好，但是离散有所增加。而高频频段区间，二者吻合相对较差，离散程度也大大增加。图中红色直线是对2种结果进行简单线性回归分析的结果，回归分析的系数列于表 1中。系数a，b, 分别是线性回归方程的偏差和斜率项(y=a+bx)，Re是相关系数，RMSD是均方根偏差，STDL是y变量关于回归方程的偏差的标准差，n是样本总数，p1和p2分别是落入距线性回归线±STDL和±2STDL的样本数目比例。总体来看，2种观测结果的相关程度非常高，相关系数为0.92。但由回归斜率可知，雷达观测整体略偏低于浮标观测。2种观测结果之间的均方根偏差为0.0045Hz，是典型的涌浪频率0.08Hz的5.6%。

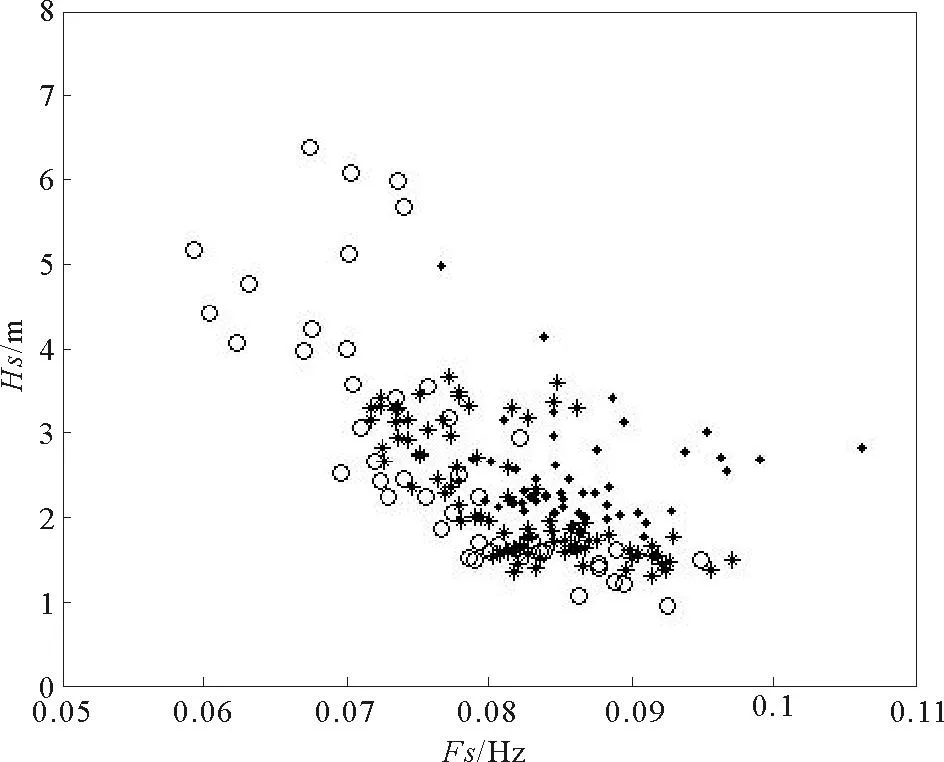
(圆圈、圆点、星号分别对应2月26—29日、3月1—3日、3月4—5日 3次涌浪事件。Circle: 2008-02-26—2008-02-29; Point: 2008-03-01—2008-03-03; Star: 2008-03-04—2008-03-05.)

图5涌浪频率与有效波高的关系图(2008-02-26—2008-03-05)

Fig.5Relationship between swell frequency and

significant waveheight

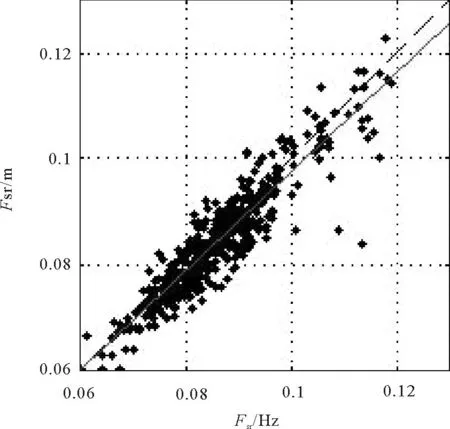
(红色直线为线性回归线。Red line is the linear regression lin.)

a/HzbReRMSD/HzSTDL/Hznp1p20.000.930.920.00450.004147873%96%

二者逐月进行对比的统计和回归分析结果列入表2。表中2—4月统计到的涌浪样本较多，而5—7月样本数较少。同时，由表中最后一列浮标观测结果在当月的均值可以观察到，从2—7月涌浪频率出现了整体上升的特点，这与冬季大西洋风暴的频发有着直接的关联。春季过后，伴随着大西洋中心的剧烈风暴减少，Iroise海区测量到的涌浪事件也显著减少。经过对数据时间序列的观察，本文证实了浮标的观测较为稳定，表中样本数的减少主要是由雷达观测数目的减少造成。由此可以推断，雷达对中低频涌浪的观测效能较高，而对于高频涌浪的探测能力显著降低，这进一步证实了图6中对该现象的分析。伴随着样本数的减少，2种观测结果之间的均方根偏差随之增大。各月份线性回归结果有一定的波动。图7展示了逐月的数据对比情形。各月份中3月的回归方程斜率为最优，而2和5月的回归方程斜率较其他月份有较大的差异。这一方面是由样本数的局限造成；另一方面，由散点图推断是由观测到的涌浪频率数据点较为集中造成。尤其是5月份，观测到的样本数非常少，而且数值非常集中。这也导致偶尔出现的偏差较大的数据点对线性回归分析结果影响较大。

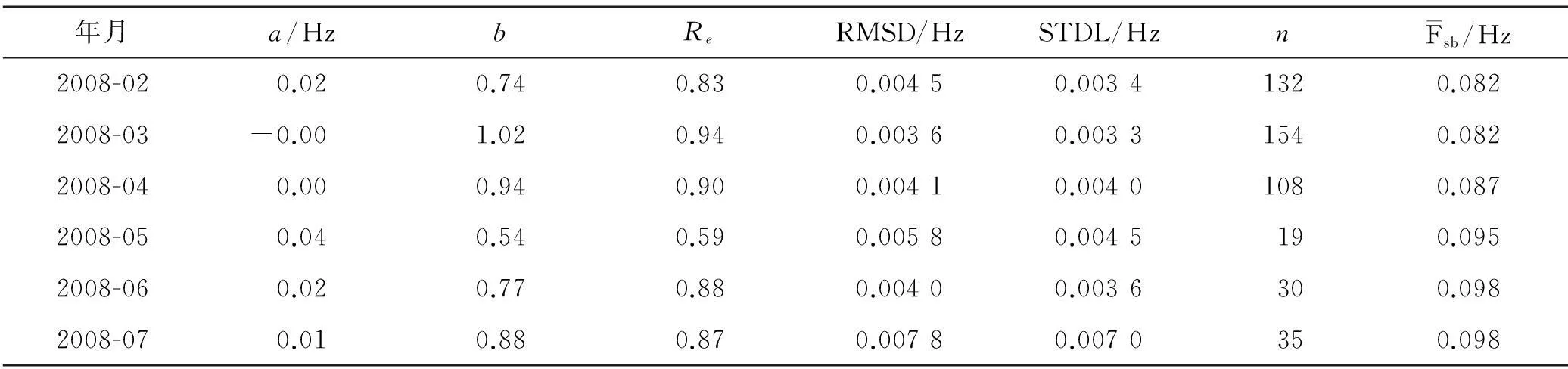
表2　雷达与浮标观测涌浪频率的线性回归分析

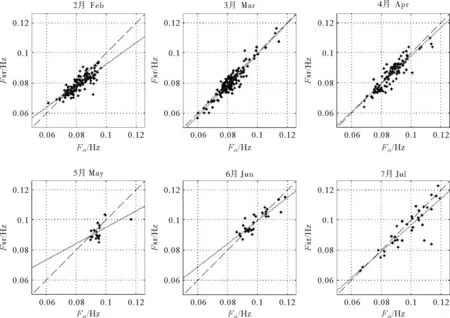
(红色直线为线性回归线。Red line is the linear regression line.)

需要指出的是，雷达本身对于海面的探测能力有波高限制。由于Barrick方程的提出基于摄动分析，其理论可探测的海面整体有效波高上限为4/k0。实际应用中，往往不采用理论极限，而是乘以系数0.3左右作为观测阈值。由此推断本文雷达的海面有效波高测量能力阈值为4.6m。因而对于实际海况超出此阈值的雷达结果，宜持以谨慎态度。

5结语

本文使用浮标数据对高频地波雷达反演涌浪频率参数的结果进行了验证。结果表明：在中低频频段，雷达计算涌浪频率结果与浮标数据吻合良好。但对于极低频涌浪，雷达测量结果的离散程度亦略有增加。雷达对高频涌浪的测量精度降低。在2—4月的冬春季节，雷达观测到的中低频率涌浪较多；而在5—7月的春夏季节，雷达观测到的涌浪数目显著减少，且多为高频成分。对于全部观测结果的统计分析表明，雷达反演结果与浮标数据相关程度较高，相关系数为0.92。二者均方根偏差为0.0045Hz，占典型涌浪频率大小的百分比为5.6%。

雷达二阶回波谱信噪比相对于一阶谱要低得多，其观测精度受到电离层、海况等外界因素影响较大。对信号更加精细化的质量控制可以进一步提高涌浪计算结果的精度。另外，雷达的测量能力与海况密切相关，恶劣海况对雷达信号造成的影响有待进一步探究。这些将是本文下一步的工作。

致谢：本文所用观测数据由法国SHOM(Service Hydrographique et Océanographique de la Marine)提供，作者对此表示诚挚谢意。

参考文献：

[1]Smedman A, Högström U, Sahleé E. Observational study of marine atmosphe ric boundary layer characteristics during swell [J]. J Atmos Sci, 2009, 66: 2747-2763.

[2]Zhang J, Wang W, Guan C. Analysis of the global swell distributions using ECMWF Re-analyses wind wave data [J]. J Ocean Univ China, 2011, 10: 325-330.

[3]Wang W, Forget P, Guan C. Inversion of swell frequency from a 1-year HF radar dataset collected in Brittany (France) [J]. Ocean Dynamics, 2014, doi:10.1007/s10236-014-0759-9.

[4]Crombie D D. Doppler spectrum of sea echo at 13.56 Mc./s [J]. Nature, 1955, 175: 681-682.

[5]Barrick D E. First-order theory and analysis of MF/HF/VHF scatter from the sea [J]. IEEE Trans Antennas Propag, 1972, 20: 2-10.

[6]Paduan J D, Cook M S. Mapping surface currents in Monterey Bay with CODAR type HF radar [J]. Oceanography, 1997, 1: 49-52.

[7]Kim S Y, Terrill E J, Cornuelle B D, et al. Mapping the U.S. west coast surface circulation: A multiyear analysis of high-frequency radar observations [J]. J Geoph Res, 2011, 116: C03011.

[8]Marmain J, Molcard A, Forget P, et al. Assimilation of HF radar surface currents to optimize forcing in the North Western Mediterranean sea [J]. Nonlinear Proc Geoph, 2014, 21: 659-675.

[9]Hasselmann K. Determination of ocean-wave spectra from Doppler radio return from the sea surface [J]. Nat Phys Sci, 1971, 229: 16-17.

[10]Barrick D E. Remote sensing of sea state by radar[M]. Derr VE ed. Remote Sensing of the Troposphere.Washington: US Government Printing Office, 1972.

[11]Lipa B, Nyden B. Directional wave information from the SeaSonde [J]. IEEE J Oceanic Eng, 2005, 30: 221-231.

[12]Gurgel K W, Essen H H, Schlic T. An empirical method to derive ocean waves from second-order Bragg scattering: prospects and limitations [J]. IEEE J Oceanic Eng, 2006, 31: 804-811.

[13]Broche P. Estimation du spectre directionnel des vagues par radar decametrique coherent [C]. Lisbon: AGARD Conference on Special Topics in HF Propagation Proc, 1979. AGARD-CP-263.

[14]Forget P, Broche P, de Maistre J C, et al. Sea state frequency features observed by ground wave HF Doppler radar [J]. Radio Sci, 1981, 16(5): 917-925.

[15]Lipa B J, Barrick D E, Maresca Jr J W. HF radar measurements of long ocean waves [J]. J Geoph Res, 1981, 86(C5): 4089-4102.

[16]Sentchev A, Forget P, Barbin Y, et al. Surface circulation in the Iroise Sea (W. Brittany) from high resolution HF radar mapping [J]. J Mar Syst, 2013, 109-110(Suppl.): 153-168.

[17]Gurgel K W, Antonischki G, Essen H H, et al. Wellen radar (WERA): a new ground-wave based HF radar for ocean remote sensing [J]. Coast Eng, 1999, 37: 219-234.

[18]Hanson J L, Phillips O M. Automated analysis of ocean surface directional wave spectra [J]. J Atmos Ocean Technol, 2001, 18: 277-293.

责任编辑庞旻

Validation of HF Radar Derived Swell Frequency Using Buoy Data

WANG Wei-Li1,2,3, GUAN Chang-Long1, Philippe Forget2,3, SUN Jian1

(1. Physical Oceanography Laboratory, Ocean University of China, Qingdao 266100, China； 2. Université de Toulon, CNRS/INSU, IRD, Mediterranean Institute of Oceanography(MIO), UM 110, 83957, La Garde Cedex, France； 3. Aix-Marseille Université, CNRS/INSU, IRD, MIO, UM 110, 13288 Marseille, France)

Abstract：The important role of swell in coastal ocean environment is being paid more and more attention. High-frequency (HF) radar provides a new way to give near-real-time observations of swell parameters. This paper compares buoy and radar derived swell frequencies during Feb-Jul, 2008 in the Iroise Sea, France. Results show that radar-inverted swell frequencies agree well with buoy measurements. The general comparison between the two measurements shows a correlation coefficient of 0.92 and a root-mean-square difference of 0.0045Hz. The majority of radar measurements are obtained from February to April with low- to moderate- frequency swell. The number of radar measurements decreases significantly for the period of May to July when swell cases have higher frequencies.

Key words:swell frequency; HF radar; WERA; buoy

中图法分类号：P731.22

文献标志码：A

文章编号：1672-5174(2016)01-001-07

作者简介：王炜荔(1987-)，女，博士生。E-mail:wangweiliee@hotmail.com

收稿日期：2015-03-16；

修订日期：2015-04-15

*基金项目：国家自然科学基金项目(41376010)；国家科技支撑计划项目(2011BAC03B01)资助

DOI：10.16441/j.cnki.hdxb.20150090

引用格式：王炜荔， 管长龙， Philippe Forget, 等. 使用浮标数据验证高频地波雷达反演涌浪频率[J]. 中国海洋大学(自然科学版)， 2016, 46(1)： 1-7.

WANG Wei-Li, GUAN Chang-Long, Philippe Forget, et al. Validation of HF Radar derived swell frequency using buoy data[J]. Periodical of Ocean University of China, 2016, 46(1): 1-7.

Supported by the National Natural Science Foundation of China(41376010); National Key Technologies R&D Program (2011BAC03B01)

**通讯作者： E-mail:clguan@ouc.edu.cn