求解最小比率旅行商问题的混合行为蚁群算法

倪郁东，赵　群，沈吟东，张玉洁（.合肥工业大学数学学院，安徽合肥　30009；.华中科技大学自动化学院，湖北武汉　430074）



求解最小比率旅行商问题的混合行为蚁群算法

倪郁东1，赵群1，沈吟东2，张玉洁1
（1.合肥工业大学数学学院，安徽合肥230009；2.华中科技大学自动化学院，湖北武汉430074）

摘要：为了快速并且有效地求解最小比率旅行商问题，文章提出了一种混合行为蚁群算法。通过对蚁群算法中转移概率以及信息素更新策略加以改进，使蚂蚁能够随机性地选择自己的行为规范，将蚁群进一步智能化；为防止陷入局部最优，算法中设计了交换策略与灾变策略。仿真实验结果表明，改进后的算法能够有效求解最小比率旅行商问题。

关键词：最小比率旅行商问题；蚁群算法；混合行为；优化

沈吟东（1965-），女，安徽合肥人，博士，华中科技大学教授，博士生导师.

旅行商问题（traveling salesman problem，TSP）是一类典型的组合优化问题，同时也是NP-Hard问题。通常可简单描述为：有一旅行商欲前往n个城市推销商品，从某一城市出发，经过各个城市一次后返回出发城市，问该旅行商应如何选择出行路线，使得总路程最短。最小比率旅行商问题（MRTSP）是从经典TSP中引申出来的一个变形问题，它在原TSP的基础上增加了收益假定，即旅行商从城市i走到城市j能获得一定收益pij，现在的问题变成：确定一条路线，使得总路程与总收益的比最小。这种思想类似于经济学中的费用效益，既考虑到了成本同时又考虑到了收益。相比于TSP中只考虑路程，研究MRTSP往往更具实际意义。

与标准TSP不同，MRTSP的目标函数是非线性的，这使得问题的求解变得更加困难。目前求解这类问题的方法主要有蚁群优化算法［1］、模拟退火算法［2］、竞争决策算法［3］以及大洪水算法［4］。蚁群算法是一类群体优化算法，虽然具有很强的全局搜索能力，但是算法的运行时间以及解的质量很难让人满意。模拟退火算法、竞争决策算法以及大洪水算法属于单点搜索优化算法，极易陷入局部最优。

本文提出的混合行为蚁群算法中，蚂蚁拥有自己的行为，能够按照自己的方式选择下一个城市。在设定信息素的更新策略时，采用了自适应蚁群算法［5］和最大-最小蚁群算法［6］各自的优点并将其混合使用。此外，为防止陷入局部最优，算法中加入了交换策略和灾变策略，最后经过算例测试对本文算法进行了验证。

1　问题模型

G（V，E）为给定的赋权完全图，V＝（1，2，…，n）表示顶点集，E＝{（i，j）| i，j∈V且i≠j}为边集。距离矩阵D＝［dij］n×n，当i≠j时，dij＝dji；当i ＝j时，dij＝＋∞。收益矩阵P＝［pij］n×n，当i≠j时，pij＝pji；当i＝j时，pij＝0。xij＝1表示边（i，j）在回路上，否则xij＝0。

MRTSP的数学模型描述如下：

其中，|S|表示集合S中含图G的顶点个数。前2条约束条件意味着每个顶点只有一条边进和一条边出，第3条约束条件说明没有产生子回路解。因此，同时满足以上3个约束条件的解能构成一条Hamilton回路。

2　混合行为蚁群算法

目前，混合行为蚁群算法已在求解车辆路径问题［7］、0-1背包问题［8］等一些领域上取得了良好的效果，能否适用于求解MRTSP是本文研究的重点。与经典TSP不同，在求解MRTSP时，启发式因子可以设定为ηij＝pij/dij。启发式因子的作用在于帮助蚂蚁以贪婪的方式选择那些收益更大、路程更短的城市。

2.1转移概率的改进

蚁群算法中，蚂蚁在经过的路径上会留下信息素，而信息素浓度的大小未必能反映出最优路径的方向，而且可能会使较差解所在路径上的信息素浓度得到不应有的加强，干扰了后续蚂蚁的寻优。因此，本文采用随机性选择的方式来改进转移概率，首先给出以下5个规则。

规则1蚂蚁k以贪婪的方式选择下一个要到达的城市j：

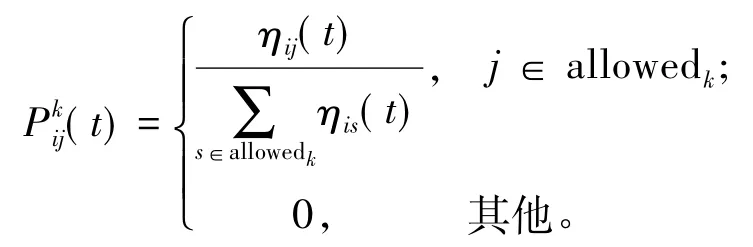
规则2选择方式只与路径上的信息素浓度有关：

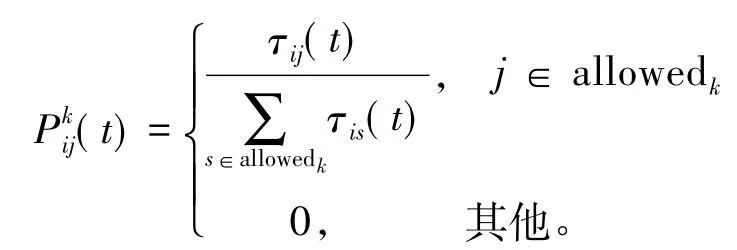
规则3采用ant-system中的转移概率：

规则4以蚂蚁自适应系统中的转移概率去选择下一个要到达的城市j：

规则5随机从allowedk中选择一个城市作为下一个要访问的城市。

蚂蚁k在进行下一个城市的选择时，从以上5个规则中随机选择一个作为自己的转移概率。

拥有混合行为的蚁群在搜索的过程中具有极强的随机性，当算法陷入局部最优时，仍有可能从局部最优中跳出，避免“早熟”现象的发生。

2.2信息素更新策略

在ant cycle system中，信息素更新策略为：

其中，ρ为信息素保留系数，取值在0～1之间；M为蚂蚁的个数；Q为蚂蚁在一个周期中携带的信息素量，通常为大于0的常数；Lk为蚂蚁k所走的路径；f（Lk）为蚂蚁k所走路径的总长度。

当问题的规模较大时，由于挥发系数（1-ρ）的存在，一些未被搜索到的路径或者很少被搜索到的路径上的信息素会一直减少甚至接近于0，从而降低了算法的搜索能力。另外，ρ过小会导致之前被搜索到的路径有更大的可能性会被再次搜索到，过大则会使算法的收敛速度降低。这里采用自适应改变ρ的值来解决以上问题，即ρ的初始值ρ（0）＝1，当算法求得的最优值在多次循环内没有变化时，ρ（t）改写为：

其中，ρmin为ρ的最小值。

2.3交换策略

在局部搜索算法中，2-opt是一类能够有效解决组合优化问题的方法。当用于解决MRTSP问题时，其基本原理为：对目前产生的最优解，随机交换2个城市点的位置，交换之后再将2个城市之间的路径反向。比如，对于n个城市的MRTSP问题，若目前的最优解为j1—j2—…—jn-1—jn—j1，其中j1，j2，…，jn为12，…，n的一个排列组合。随机交换2个城市点的位置，不妨设为ji和jk，则交换后的解为j1—j2…ji-1—jk-jk-1…—ji—jk＋1…jn—j1。若实行2-opt交换能够使目标函数变小，则进行交换，否则保持原最优路径不变。

2.4灾变策略

蚁群算法在拥有较快搜索速度的同时，也容易陷入局部最优。为此，考虑蚂蚁搜索到食物后，如果在搜索食物的路上遇到障碍，比如自然灾害，蚂蚁依然能够通过更换路径找到食物。因此，通过引入灾变算子来解决算法的“早熟”问题。

灾变算子的设计方法与遗传算法中的变异类似。当多次得到的是相同的结果、算法倾向于陷入局部最优时，引入灾变。在局部最优路径上选择一段或者若干段，让这些路径上的信息素大幅减少。于是蚂蚁在下次搜索的过程中，有更大概率放弃该段路径转而去寻找更好的路径。在发生灾变路径的选择上，与遗传算法类似，采用小随机概率来决定，因为如果发生灾变的路径过多，可能会导致蚂蚁的搜索过程往坏的方向发展。

2.5算法流程

（1）参数初始化。每条路径上的信息素τij（0）＝c，c为常数。迭代计数器N＝0，最大迭代次数Nmax＝max；

（2）将M只蚂蚁随机放到n个城市中，为每只蚂蚁建立禁忌表并把它们当前所在的第1个城市记录在禁忌表中。

（3）蚂蚁从所在的第一个城市出发，依照2.1中的转移概率选择下一个访问的城市并将该城市记录在对应的禁忌表中。

（4）重复步骤（3），直至访问完所有城市，这样就形成了M条闭合的回路，即L1，L2，…，LM。

（5）分别计算L1，L2，…，LM对应的目标函数值f（L1），f（L2），…，f（LM）。将最小目标函数值所对应的路径实施n次2-opt交换，保存此时的最优路径Llocal。

（6）按照2.2中的策略对路径上的信息素进行更新。更新完成后，采用MMAS算法与信息素平滑的思想，当τij＞τmax时，置τij＝τmax；当τij＜τmin时，置τij＝（τmax＋τmin）/2，便于蚂蚁发现新的路线。τmax＝Q/f（Llocal），τmin＝τmax/2M。

（7）判断是否连续m次迭代得到的是相同的最优路径。若是则以概率P对Llocal上的路径实行灾变策略，被灾变所影响的路径上的信息素为τmin。m＝Nmax/10，P＝0.1。

（8）比较本次迭代的最优路径Llocal与全局最优路径Lglobal，若f（Llocal）＜f（Lglobal），置Lglobal＝ Llocal。

（9）N＝N＋1，判断N＜Nmax，若是则重复步骤（2）至步骤（8），否则流程结束，输出Lglobal以及f （Lglobal）。

3　算例分析

运用文献［4］中的2个算例测试本文算法的性能。经Matlab实验调试，算法参数设置为：α＝1，β＝5，ρmin＝0.5，a＝0.1。算例1中Q＝0.7；算例2中Q＝0.5，各路径初始信息素c＝1。蚂蚁的个数M＝50，最大迭代次数Nmax＝300。

算例1设G（V，E）为给定的赋权完全图，距离矩阵D与收益矩阵P如下所示：

算例2设G（V，E）为给定的赋权完全图，距离矩阵D与收益矩阵P如下所示：

已知目前2个算例的最优解分别为0.639 10 和0.408 71。运用本文算法对2个算例分别运行10次，均获得了最优解。

算例1的最优路径为1—4—6—7—5—8—2—3—1，总路程为255，总收益为399。

算例2的最优路径为1—4—2—6—5—3—7—10—9—8—1，总路程为2 845，总收益为6 961。

为了便于比较，将算例分别在大洪水算法（great deluge algorithm，GDA）、竞争决策算法（competitive decision algorithm，CDA）、改进遗传算法［9］（improved genetic algorithm，IGA）以及改进蚁群算法［10］（improved ant colony algorithm，IACA）上运行10次，运行结果见表1所列。

通过比较5种算法得到的结果可以发现，无论是从获得最优解的次数还是解的整体质量上来看，本文算法要明显优于另外的4种算法。此外，从获得最优解的平均耗时来看，本文算法也略胜一筹。

表1　实验结果

4　结束语

作为从经典TSP引申出来的扩展问题，MRTSP在国内的研究还比较少。本文提出的混合行为蚁群算法可以在保证收敛速度的情况下提高解的质量，为求解MRTSP提供了新的思路。

［参考文献］

［1］Dorigo M，Maniezzo V，Colorni A.Ant system：optimization by a colony of cooperating agents［J］.IEEE Trans on Systems，Man and Cybernetics，1996，26（1）：29-41.

［2］马良.求解最小比率TSP的一个算法［J］.系统工程，1998，16（4）：62-65.

［3］宁爱兵，马良.最小比率旅行商（MRTSP）问题竞争决策算法［J］.计算机工程与应用，2005，41（11）：30-32.

［4］盛虹平.求解最小比率旅行商问题的大洪水算法［J］.杭州师范大学学报：自然科学版，2010，9（6）：401-405.

［5］王颖，谢剑英.一种自适应蚁群算法及其仿真研究［J］.系统仿真学报，2005（1）：31-33.

［6］St¨utzle T，Hoos H.MAX-MIN ant system and local search for the traveling salesman problem［C］//IEEE International Conference on Evolutionary Computation，1997.IEEE，1997：309 -314.

［7］何文玲，倪郁东，汪婷婷.基于混合行为蚁群算法的车辆路径问题［J］.合肥工业大学学报：自然科学版，2014，37（7）：883-887.

［8］潘夏福.混合蚁群算法求解0-1背包问题［D］.厦门：厦门大学，2008.

［9］周泽岩，张喜.基于改进遗传算法的TSP问题求解的研究［J］.物流技术，2012，31（9）：220-223.

［10］王忠英，白艳萍，岳利霞.经过改进的求解TSP问题的蚁群算法［J］.数学的实践与认识，2012，42（4）：133-140.

（责任编辑马国锋）

Mixing behavior ant colony algorithm for solving minimum ratio traveling salesman problem

NI Yu-dong1，ZHAO Qun1，SHEN Yin-dong2，ZHANG Yu-jie1
（1.School of Mathematics，Hefei University of Technology，Hefei 230009，China；2.School of Automation，Huazhong University of Science and Technology，Wuhan 430074，China）

Abstract：In order to optimize the minimum ratio traveling salesman problem（MRTSP）quickly and effectively，a kind of mixing behavior ant colony optimization（ACO）is proposed.By improving ACO’s transition probabilities and strategy of updating pheromone，every ant can select its behavior rules randomly，which makes the ant colony more intelligentialized.Exchange strategy and catastrophe strategy are designed in the algorithm to avoid falling into local optimum.The results of simulation experiment indicate that the modified algorithm can optimize MRTSP effectively.

Key words：minimum ratio traveling salesman problem（MRTSP）；ant colony optimization（ACO）；mixing behavior；optimization

作者简介：倪郁东（1963-），男，安徽合肥人，合肥工业大学副教授，硕士生导师；

基金项目：国家自然科学基金资助项目（71171087）；合肥工业大学教学研究资助项目（XJ2009005）

收稿日期：2014-12-26；修回日期：2015-03-23

Doi：10.3969/j.issn.1003-5060.2016.01.026

中图分类号：TP301.6

文献标识码：A

文章编号：1003-5060（2016）01-0140-05