基于PSO算法的定速风电机组三质块传动系统模型参数辨识

王　慧，潘学萍，鞠　平（河海大学能源与电气学院，江苏南京　211100）



基于PSO算法的定速风电机组三质块传动系统模型参数辨识

王慧，潘学萍，鞠平
（河海大学能源与电气学院，江苏南京211100）

摘要：为获得传动系统模型的准确参数，提出阵风激励下三质块传动系统模型的参数辨识方法。根据定速风电机组机械动态与电气动态解耦的特性，提出在辨识传动系统模型参数时可忽略电气动态，据此获得定速风电机组的简化模型。采用轨迹灵敏度方法，分析了传动系统各参数的可辨识性及辨识的难易程度。基于粒子群优化算法（PSO）对传动系统模型进行了参数辨识。辨识结果与轨迹灵敏度分析结论一致，验证了提出的参数辨识方法的可行性。

关键词：定速风电机组；三质块传动系统；阵风风速；轨迹灵敏度；参数辨识；粒子群优化算法

随着风力发电技术的快速发展，风电在电网中所占比例不断增加，对电力系统安全稳定的影响也日益显著。定速风电机组的发电机定子与电网直接相连［1］，传动系统对其动态特性具有明显影响，因此建立详细的传动系统模型并获得准确的模型参数，对分析并网风电机组的动态特性非常重要。

风电机组的传动系统由风力机、变速箱、大轴以及它们之间的连接部件组成，目前已有的传动系统模型包括六质块、三质块、两质块以及单质块模型［2］。当分别对风力机的三只叶片、轮毂、齿轮箱以及发电机转子这6个质量块建模时，便为六质块模型。该模型的精度高，但比较复杂，一般在分析风力机的气动特性时使用，而在研究风电机组并网后的动态特性时较少使用。目前在研究风电机组并网动态特性时，常采用两质块或单质块传动系统模型。两质块模型将风力机与传动齿轮箱等效成一个集中质量块，发电机转子为另一个质量块，忽略了风力机叶片与传动齿轮箱之间的扭振［2-3］。单质块模型将风力机、传动齿轮箱以及发电机转子等效成一个集中质量块，忽略了风力机与发电机转子之间的扭振，模型较为简单［4-5］。三质块模型将风力机、齿轮箱以及发电机转子分别等效为一个集中质量块，目前对于该模型的研究较少。

目前风电机组参数辨识研究方面大多侧重于发电机及控制器部分，如金宇清等［6］辨识了双馈感应风电机组的电气参数；王鸿山［7］研究了风电机组中控制器的参数辨识技术。在传动系统模型参数的辨识方面，潘学萍等［8］基于阶跃风速激励，辨识了两质块传动系统模型参数。笔者基于潘学萍等［8］的研究，提出采用阵风激励辨识风电机组的三质块传动系统模型参数。首先基于轨迹灵敏度方法分析了传动系统模型参数的可辨识性和辨识的难易度，然后采用粒子群优化算法对模型参数进行辨识。

1　传动系统模型

定速风电机组的发电机定子与电网直接相连，传动系统对风电机组的动态特性影响较大。风电机组传动系统主要由风力机叶片、轮毂、低速传动轴、齿轮箱、高速传动轴和发电机等构成［9-12］，见图1。

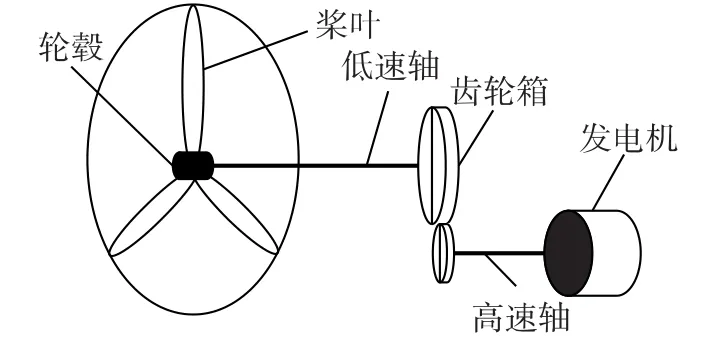
图1　风电机组传动系统结构Fig.1 Structure of drive-train system for wind turbine generators

1.1风能转化模型

风力机将捕获的风能转化成旋转的机械能，带动发电机转子转动产生电能。风力机从风能中捕获的机械功率Pm为

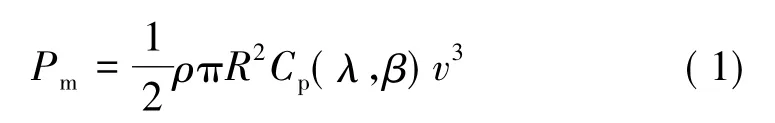
式中：ρ——空气密度；R——风轮叶片半径；Cp（λ，β）——风能利用系数；λ——叶尖速比；β——桨距角；v——风速。

根据式（1）可知，在风速一定的情况下机械功率主要取决于风能利用系数。风能利用系数常采用的经验计算公式见文献［10］。

图2　三质块传动系统模型结构Fig.2 Structure of three-mass drive-train model

1.2三质块传动系统模型

三质块传动系统模型将风力机、齿轮箱以及发电机转子等效为一个集中质量块，如图2［13-14］所示，图中Tw为风力机的机械转矩，Hbh、Hgb、Hg分别为风力机、齿轮箱和发电机转子的等效集中质量块的惯性常数，Dls、Dhs分别为风力机与齿轮箱、齿轮箱与发电机转子之间的阻尼系数，Kls为连接风力机和齿轮箱的低速轴的等效刚度系数，Khs为连接齿轮箱和发电机的高速轴的等效刚度系数。

动力学方程为［14］

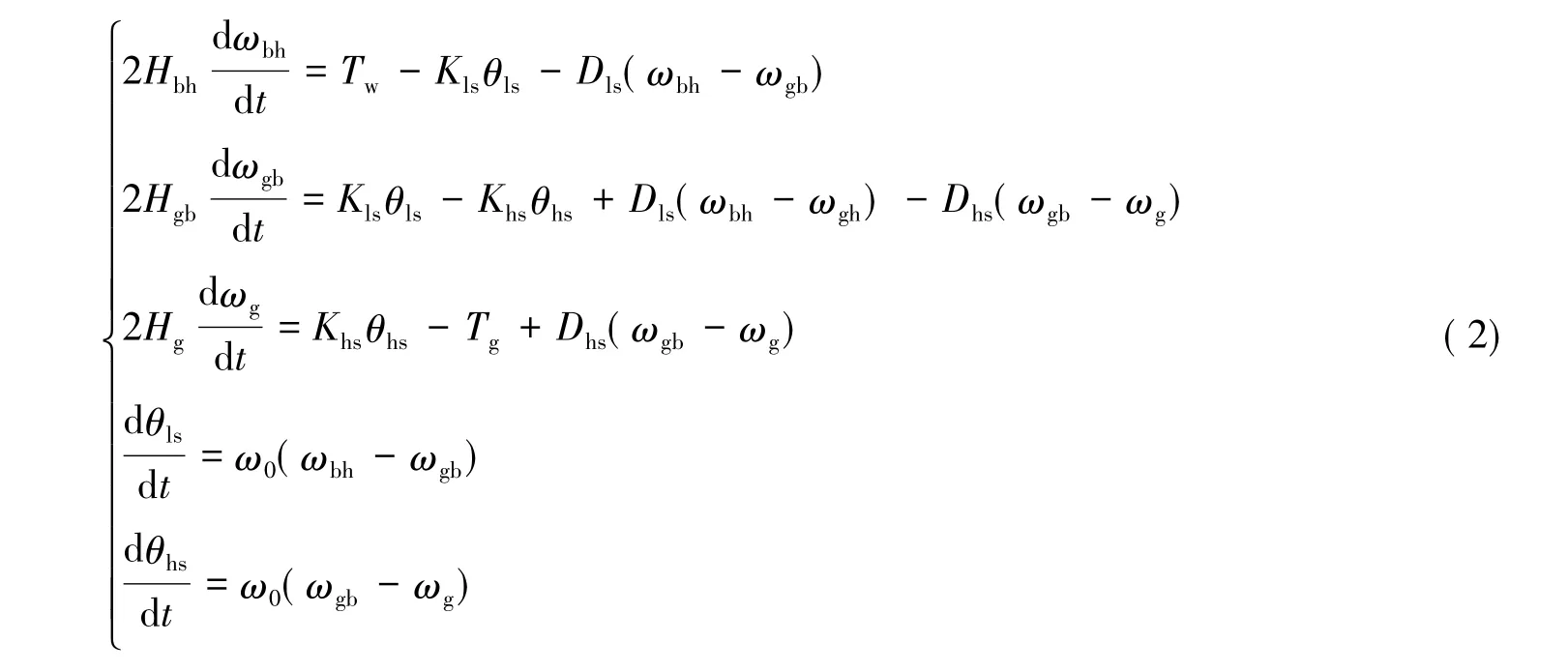
式中：ωbh、ωgb、ωg——风力机、齿轮箱和发电机转子的等效集中质量块的电角速度；ω0——系统电角速度的基值；θls、θhs——风力机相对于齿轮箱的角位移及齿轮箱相对于发电机转子的角位移；Tg——发电机输出的电磁转矩。

2　传动系统模型参数的可辨识性及辨识难易度分析

常采用轨迹灵敏度方法分析参数的可辨识性及参数辨识的难易度。如果若干个参数的轨迹灵敏度同时过零点，则可以判定这些参数相关，即不是唯一可辨识；如果所有参数的灵敏度都不同时过零，也不线性相关，则可以判定所有参数不相关，即唯一可辨识［15］。如果轨迹灵敏度曲线出现振荡，并且同时过零点，意味着振荡过程会同相或者反相。同时，参数轨迹灵敏度的大小反映了参数辨识的难易程度。

2.1阵风激励下发电机转速受扰轨线

以图3所示的单机无穷大系统（OMIB）为例，风电机组G通过升压变T，经双回输电线路L接入无穷大系统。其中，风力机参数如下：Hbh＝4.0s，Hgb＝0.3s，Hg＝0.5 s，Khs＝4.0pu/rad，Kls＝3.0pu/rad，Dhs＝1.0pu，Dls＝1.0pu。发电机参数如下：定子电阻Rs＝0.018pu，定子电抗Xs＝0.217 pu，转子电阻Rr＝0.014 pu，转子电抗Xr＝0.186 pu，激磁电抗Xm＝7.280 pu。风电机组出口升压变电抗Xt＝0.084 2 pu，补偿电路容抗Xc＝4.1701pu，线路电阻Rl＝0.00047pu，线路电抗Xl＝0.00190pu。

潘学萍等［8］指出：对于定速风电机组，由于机械动态与电气动态的耦合较弱，风速激励下风电机组由机械动态主导。因此在风速激励下辨识传动系统参数时，可忽略发电机动态，即将发电机采用准稳态模型表示，如图4所示，图中.U为无穷大母线电压，s为滑差。

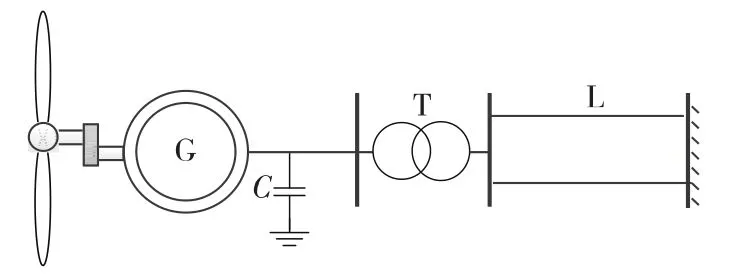
图3　含单台风电机组的单机无穷大系统Fig.3　 One-machine infinite-bus（OMIB）system with single wind turbine generator

图4　风电机组接入系统等效电路Fig.4 Equivalent circuit for wind turbine generator integrated with system

以图3所示系统为例，采用图5所示阵风作为激励，基本风速为7m/s，在t＝0.5 s出现阵风，持续3 s结束，阵风峰值为10m/s。以发电机转子转速作为观测量，阵风激励下的受扰轨线如图6所示。

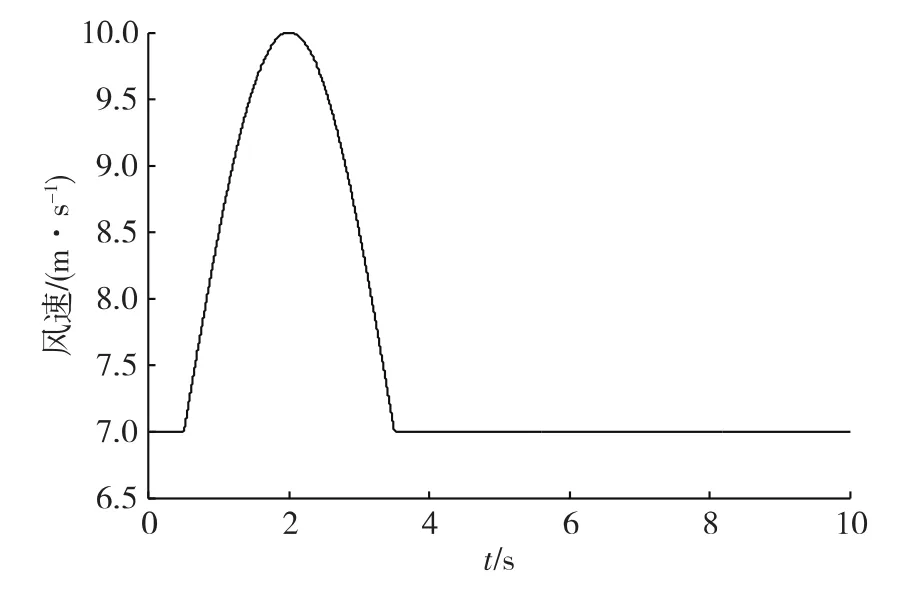
图5　阵风风速曲线Fig.5 Speed curve of gusty wind

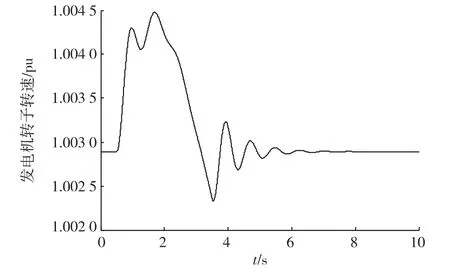
图6　发电机转子转速曲线Fig.6 Rotor speed curve of generator

2.2参数的轨迹灵敏度

依据轨迹灵敏度的定义［15］，以发电机的转速作为观测量，阵风激励下各参数的轨迹灵敏度曲线如图7所示。

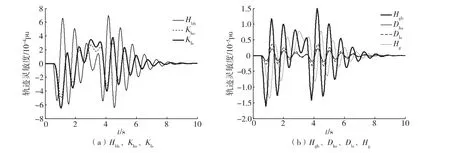
图7　参数的轨迹灵敏度曲线Fig.7 Trajectory sensitivities of parameters

从图7可以看出：参数Khs和Kls的轨迹灵敏度曲线同时过零，但其余各参数未出现该现象。根据参数的可辨识性理论可知参数中Khs和Kls不可区分辨识。因此在后续的参数辨识时，将Kls设为已知，辨识参数Khs（也可将Khs设为已知，辨识参数Kls）及其他5个参数。

也可根据轨迹灵敏度的大小分析参数辨识的难易度。在时间口0～10 s内，计算得到参数Hbh、Hgb、Hg、Khs、Kls、Dhs、Dls的灵敏度分别为4.60×10-4、1.44×10-5、4.21×10-6、2.00×10-4、2.44×10-4、1.52×10-6、2.41× 10-6。通过比较各个参数轨迹灵敏度的数值大小得出以下结论：Hbh、Hgb、Kls以及Khs轨迹灵敏度较大，容易辨识；Hg、Dls、Dhs的灵敏度较小，难以辨识。

3　传动系统模型参数的辨识

基于阵风激励，ωg为观测变量，采取粒子群优化算法辨识三质块传动系统模型的参数α＝［Hbh，Hgb，Hg，Khs，Dhs，Dls］。参数辨识的目标是寻找一组α，使得仿真轨线ωg_sim与真实轨线ωg_real之间的误差最小。目标函数为

PSO算法是基于群体的优化方法，它将每个粒子看作是D维搜索空间中的一个点，在搜索空间中以一定的速度飞行，这个速度根据它本身及同伴的飞行经验动态调整。第i粒子表示为Xi＝（xi1，xi2，…，xiD），它经历过的最好位置（有最好的适应度值）记为Pi＝（pi1，pi2，…，piD）。群体中所有粒子经历过的最好位置记为Pg＝（pg1，pg2，…，pgD）。第i粒子i的速度用Vi＝（vi1，vi2，…，viD）表示。对每个粒子，根据式（4）更新其速度和位置［16-17］。

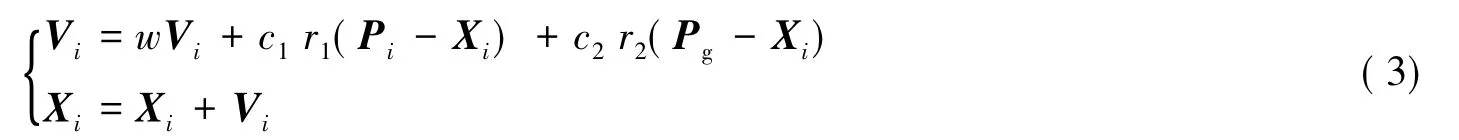
式中：w——惯性权重；c1、c2——学习因子；r1、r2——在［0，1］范围里变化的随机数。

根据经验值，取w＝0.6，c1＝c2＝2。搜索空间的维度D（待辨识参数个数）取为6。基于PSO算法辨识风电机组三质块传动系统模型参数的步骤如下：（a）仿真得到阵风激励下发电机转速的受扰轨线；（b）初始化一群粒子，设置种群的大小、初始位置和速度；（c）根据式（3）的目标函数评价每个粒子的适应度；（d）根据式（4）更新每个粒子的速度和位置；（e）重复步骤（c）和（d），直到满足收敛判据。

本文粒子的种群大小为50，待辨识参数的搜索区间在真值的［-30%，＋40%］范围内。待辨识参数的真实值如下：Hbh＝4.0s，Hgb＝0.3s，Hg＝0.5 s，Kls＝3.0 pu/rad，Dhs＝1.0 pu，Dls＝1.0 pu；辨识值如下：Hbh＝4.04 s，Hgb＝0.32s，Hg＝0.45s，Kls＝2.73pu/rad，Dhs＝0.83pu，Dls＝0.82pu。

从参数辨识的结果可以看出，Hbh、Hgb、Kls的辨识精度较高，Hg、Dhs、Dls的辨识精度稍差。参数辨识的结果与轨迹灵敏度分析的结论一致。

为了分析参数的辨识效果，将辨识结果代入算例模型进行仿真，得出辨识参数和真实参数2种情况下，风电机组在阵风激励下发电机转子转速的受扰轨线，如图8所示。由图8可知，两轨线的差异度很小，说明了本文方法的可行性。

4　结　　语

基于阵风激励下的发电机转速受扰轨线，采用轨迹灵敏度方法分析了风电机组三质块传动系统参数的可辨识性和辨识难易程度，得出以下结论：（a）参数Khs、Kls不可区分辨识；（b）Hbh、Hgb、Khs、Kls的轨迹灵敏度较大，容易辨识；Hg、Dhs、Dls的灵敏度很小，难以辨识。

采用粒子群优化算法，辨识了三质块传动系统模型的参数，参数的辨识精度与轨迹灵敏度结论一致，验证了本文提出的传动系统参数辨识方法的可行性。

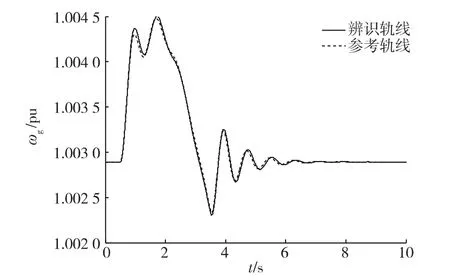
图8　辨识曲线和参考曲线对比Fig.8 Comparison of identified curve and reference curve

参考文献：

［1］AKHMATOV V.风力发电机用感应发电机［M］.风力发电机用感应发电机翻译组，译.北京：中国电力出版社，2010：15-21.

［2］MUYEEN S M，ALI M H，TAKAHASHI R，et al.Comparative study on transient stability analysis of wind turbine generator system using different drive train models［J］.IET Renewable Power Generation，2007，1（2）：131-141.

［3］刘其辉，韩贤岁.双馈风电机组模型简化的主要步骤和关键技术分析［J］.华东电力，2014，42（5）：839-845.（LIU Qihui，HAN Xiansui.Main steps and key technology of the simplified model for doubly-fed induction generator［J］.East China Electric Power，2014，42（5）：839-845.（in Chinese））

［4］陈爱.双馈风力发电仿真实验平台风机参数辨识［D］.哈尔滨：哈尔滨工业大学，2013.

［5］李辉，叶仁杰，高强，等.传动链模型参数对双馈风电机组暂态性能影响［J］.电机与控制学报，2010，14（3）：24-30.（LI Hui，YE Renjie，GAO Qiang，et al.Influence of models and parameters on transient performance of a wind turbine with DFIG［J］.Electric Machines and Control，2010，14（3）：24-30.（in Chinese））

［6］金宇清，赵泽，鞠平，等.双馈感应风力发电机的参数辨识分析［J］.高电压技术，2011，37（7）：1700-1705.（JIN Yuqing，ZHAO Ze，JU Ping，et al.Analysis on the identification of doubly fed induction generator［J］.High Voltage Engineering，2011，37（7）：1700-1705.（in Chinese））

［7］王鸿山.风力发电机控制中的参数辨识技术［D］.合肥：合肥工业大学，2010.

［8］潘学萍，高远，金宇清，等.风电机组驱动系统参数辨识［J］.电网技术，2013，37（7）：1990-1994.（PAN Xueping，GAO Yuan，JIN Yuqing，et al.Parameter identification of drive system for fixed-speed wind power generation units［J］.Power System Technology，2013，37（7）：1990-1994.（in Chinese））

［9］TRUDNOWSKI D J，KHAN J M，PETRITZ E M.Fixed-speed wind generator and wind park modeling for transient stability studies［J］.IEEE Transactions on Power Systems，2004，19（4）：1911-1917.

［10］王荷生.风电场等值建模及其暂态运行特性研究［D］.重庆：重庆大学，2010.

［11］SALMAN S K，TEO A L J.Windmill modeling consideration and factors influencing the stability of a grid-connected wind power based embedded generator［J］.IEEE Transactions on Power Systems，2003，18（2）：793-802.

［12］徐琼璟，徐政.PSS/E中的风电机组通用模型概述［J］.电网技术，2010，34（8）：176-182.（XU Qiongjing，XU Zheng.A survey on general models of wind turbine generators in PSS/E［J］.Power System Technology，2010，34（8）：176-182.（in Chinese））

［13］YE Renjie，LI Hui，CHEN Zhe，et al.Comparison of transient behaviors of wind turbines with DFIG considering the shaft flexible models［C］//GU C L，YANG K，WANG J.International Conference on Electrical Machines and Systems.Wuhan：IEEE，2008：2585-2590.

［14］丁明，王冬君，韩平平，等.风力发电传动系统通用化建模方法研究［J］.电网技术，2013，37（10）：2881-2887.（DING Ming，WANG Dongjun，HAN Pingping，et al.Research on generalized modeling method of wind power drive-train system［J］.Power System Technology，2013，37（10）：2881-2887.（in Chinese））

［15］鞠平.电力系统建模理论与方法［M］.北京：科学出版社，2010：215-300.

［16］刘永康，潘学萍，鞠平.基于改进粒子群算法的双馈感应发电机参数辨识［J］.河海大学学报（自然科学版），2014，42 （3）：273-277.（LIU Yongkang，PAN Xueping，JU Ping.Identification of DFIG parameters based on improved PSO algorithm［J］.Journal of Hohai University（Natural Sciences），2014，42（3）：273-277.（in Chinese））

［17］TRELEA I.The particle swarm optimization algorithm：convergence analysis and parameter selection［J］.Information Processing Letters，2003，85（6）：317-325.

Parameter identification of three-mass drive-train system for fixed-speed wind turbine generator based on PSO algorithm

WANG Hui，PAN Xueping，JU Ping
（College of Energy and Electrical Engineering，Hohai University，Nanjing211100，China）

Abstract：In order to obtain accurate parameters for a drive-train model，a method for parameter identification of a three-mass drive-train system with gusty wind excitation is proposed.According to the decoupling of the mechanical dynamics and electrical dynamics of fixed-speed wind turbine generators，the electrical dynamics can be neglected when identifying parameters of a drive-train model.Based on this，a simplified model for fixed-speed wind turbine generators was obtained.The identifiability of the parameters of the drive-train system and the difficulties in parameter identification were analyzed with the trajectory sensitivity analysis method.Finally，the parameters of the drive-train model were identified based on the particle swarm optimization（PSO）algorithm.The identified results are consistent with the trajectory sensitivity analysis results，verifying the feasibility of the proposed parameter identification method.

Key words：fixed-speed wind turbine generator；three-mass drive-train system；gusty wind speed；trajectory sensitivity；parameter identification；particle swarm optimization algorithm

通信作者：潘学萍，教授。E-mail：xueping_pan@163.com

作者简介：王慧（1990—），男，硕士研究生，主要从事风力发电机组建模等研究。E-mail：wangh09@sina.cn

基金项目：国家自然科学基金重大项目（51190102）；国家自然科学基金（51207045）

收稿日期：2015-03-02

DOI：10.3876/j.issn.1000-1980.2016.01.014

中图分类号：TM315

文献标志码：A

文章编号：1000-1980（2016）01-0084-05