规则波致剪切波的时空变化

季海嘉，任春平，2，蒋利君（.太原理工大学水利科学与工程学院，山西太原　030024；2.天津大学水利工程安全与仿真国家重点试验室，天津　300072）



规则波致剪切波的时空变化

季海嘉1，任春平1，2，蒋利君1
（1.太原理工大学水利科学与工程学院，山西太原030024；2.天津大学水利工程安全与仿真国家重点试验室，天津300072）

摘要：基于物理模型试验、小波变换理论及剪切不稳定理论等，研究入射波为规则波、地形为平直斜坡情况下的剪切波时空变化特性。通过对15个不同波况下的剪切波流速时间历程的小波谱进行分析，得出如下结论：入射波为规则波、地形为平直斜坡情况下可以观测到剪切波，但是时空变化不明显；剪切波产生后随时间的变化呈现连续性；剪切波在沿岸方向的能量谱中比在垂直岸线方向能量谱中占优势；地形坡度增加会使剪切波产生的区域减小；无论是1∶40坡还是1∶100坡，由剪切不稳定引起的剪切波频率都在约0.015 Hz左右变化。

关键词：剪切波时空变化；规则波；小波变换理论；剪切不稳定理论；小波谱

沿岸流［1］是波浪斜向传向海岸时在破裂过程当中发生的平行于海岸的单向水流。近些年来，人们研究发现沿岸流存在不稳定现象，Oltman-Shay等将这种现象称为剪切波［2］。剪切波最早是由Oltman-Shay等［3］于1989年通过SUPERDUCK现场沿岸流试验观测到，其数据分析表明观测到的沿岸流低频振荡与重力波（边缘波、漏失波）的特征不符。

1997年Reniers等［4-5］在实验室内利用谱分析方法对剪切波的频域特性进行了分析研究，结果表明在入射波为规则波、入射地形为有坝剖面的情况下，观测到了剪切波。但是他们只是在有坝地形上观测到了剪切波，在平直斜坡上并没有观测到。2004年Noyes等［6］对现场观测到的剪切波进行详细分析，同时也证明了观测到的低频振荡是剪切波。

目前，国内对剪切波的研究首先是由邹志利等［7］、金红等［8］进行的，他们研究发现入射地形为平直斜坡情况下沿岸流随时间是周期性变化的。任春平等［9］给出了在不规则波、入射地形为平直斜坡情况下剪切波的变化特性。

目前，关于规则波入射时是否能产生剪切波的相关研究还未见报道。Bowen等［10］认为剪切波产生的动力是时均沿岸流在垂直岸线方向的剪切力Vx（V为时均沿岸流，x为垂直岸线方向的坐标）。自该理论提出后，大部分学者都根据该理论来描述剪切波的特征，根据该理论只要时均沿岸流在垂直岸线方向上的Vx存在极值就可以产生剪切波。为了验证该理论，笔者通过试验研究规则波入射情况下是否会产生剪切波，以期验证并丰富该理论。

1　试验简介

试验在大连理工大学多功能综合水池进行，水池长55m、宽34m、深1.0m，试验布置如图1所示。试验地形采用1∶40和1∶100这2种不同坡度的平直海岸模型，海岸线与造波板成30°角，以增加海岸线的长度。流速仪垂直于海岸线排成2列，每列16个，间隔为0.5 m和1.0 m。详细试验介绍见文献［11］。

为了研究在规则波情况下剪切波的变换特性，沿岸流试验［11］设置了15个规则波波况（表1）。受篇幅所限，图2（a）和（b）为2个波况（波况6、13）在垂直岸方向和沿岸方向6个位置处的流速（垂直方向为u，沿岸方向为v）时程曲线，图中x代表流速仪距岸线的距离。这2个波况对应的入射波周期、入射波高基本相近。以这2个波况来研究坡度对剪切波的影响，并通过对其他波况进行分析，研究规则波情况下剪切波随时间、空间、地形的变化。

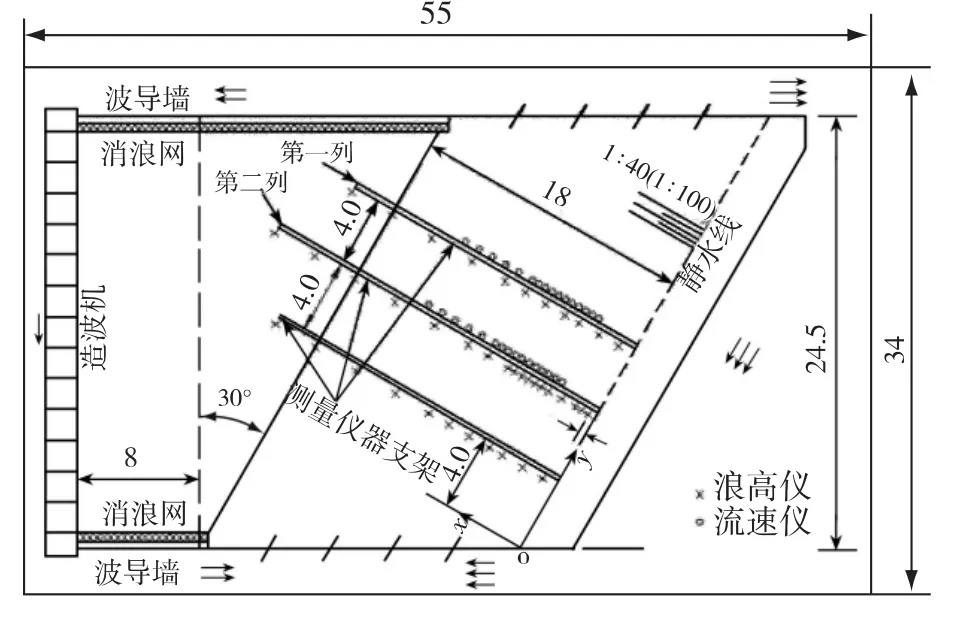
图1　沿岸流试验布置（尺寸单位：m）Fig.1 Experimental arrangement of along shore current

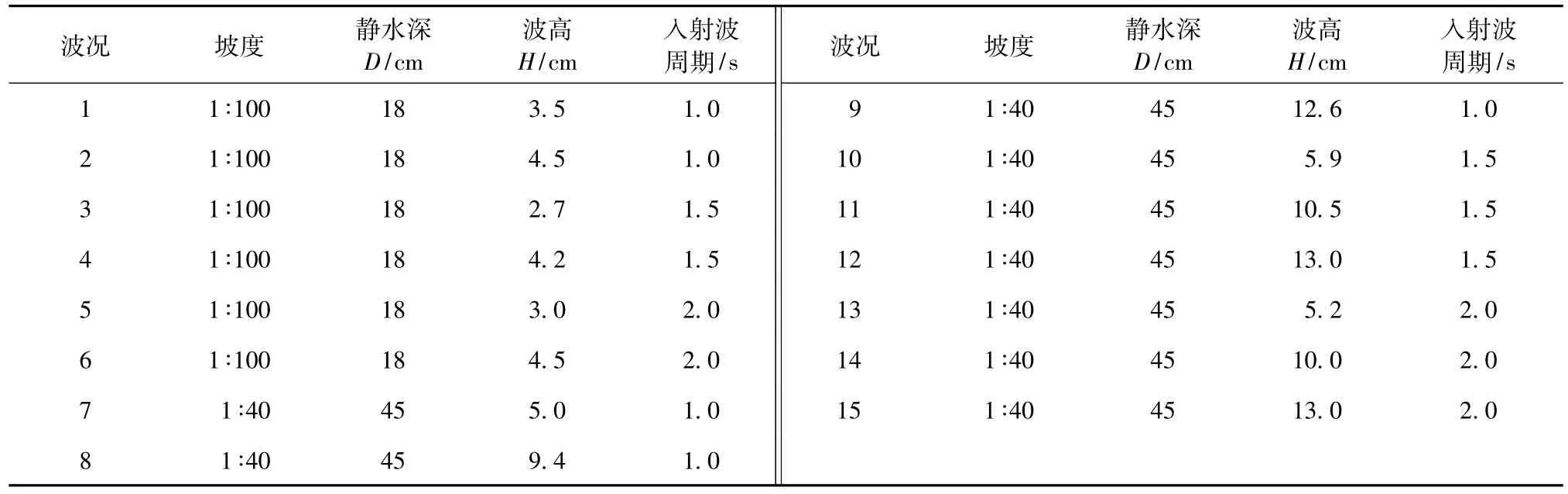
表1　波况参数Table 1 Wave parameters

2　小波变换基本理论

2.1小波变换

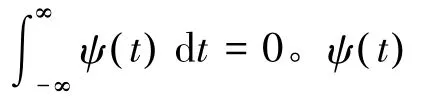
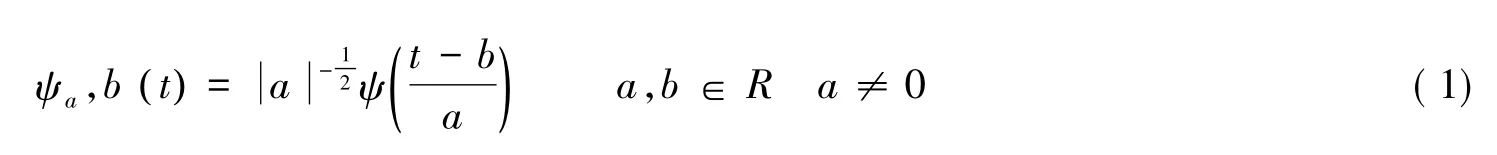
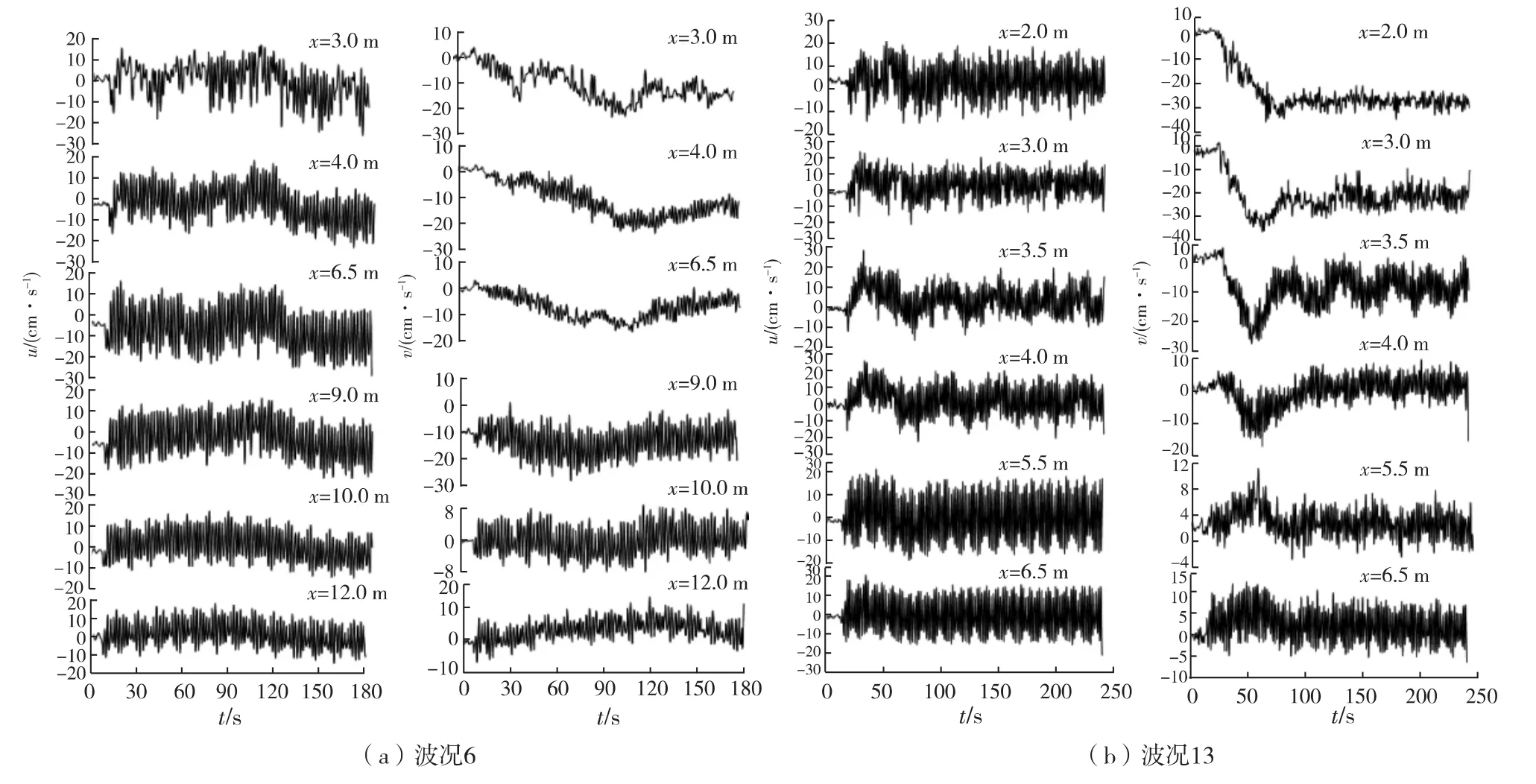
图2　波况6和波况13中6个位置处的流速时间历程Fig.2 Wave velocity time history at six locations of case 6 and case 13

小波变换包括连续小波变换和离散小波变换。对于信号f( t )∈L2(R )，其连续小波变换为

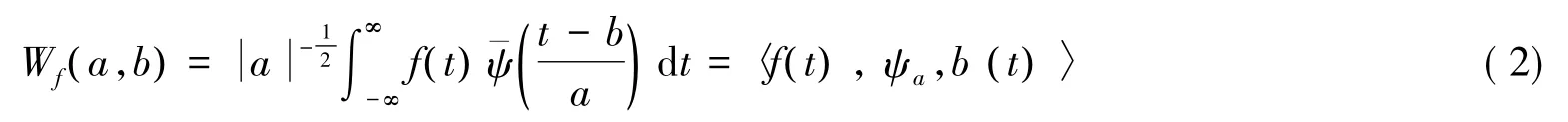
式（2）说明小波变换使用不同滤波器对信号进行滤波。在试验中得到的信号通常是离散的，所以使用离散小波变换的方法进行流速时间历程的小波变换，即时间序列f( iΔt )（i＝1，2，…，N；N为样本容量，Δt为采样时间间隔），则式（2）的离散表达形式为

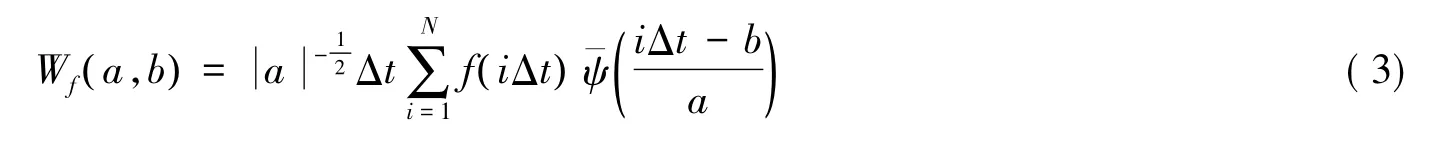
Wf(a，b )是时间序列f( iΔt )通过单位脉冲响应的滤波器输出，它包含了f( t )的信息和ψa，b（t）的信息，能同时反映时域参数b和频域参数a的特性。所以，小波变换具有时频局部化能力，可以实现信号的时频多分辨功能。

小波变换以选择合适的基本小波函数为前提，不同情况需要不同的小波函数。在实际应用中主要有2种方法选择合适的小波函数：（a）通过经验或连续的试验（对结果进行对比分析）来选择；（b）通过参照研究目标的分布形态来选取与待分析序列形态近似的小波函数［9］。本文中Morlet小波与所分析的沿岸流速时间历程形态近似，故选用Morlet复小波作为基本小波函数：

式中：ω0——中心圆频率，ω0＞5.5方可符合小波变换的允许性条件［12］。

2.2小波谱

小波谱［13-14］能够表征信号的局部时-频能量大小，从而分析并提取信号的特征。小波函数ψ0(t )一般是复函数，小波变换Wf(a，b )也是复函数，这样由式（2）能够得到小波变换的幅度和相位：

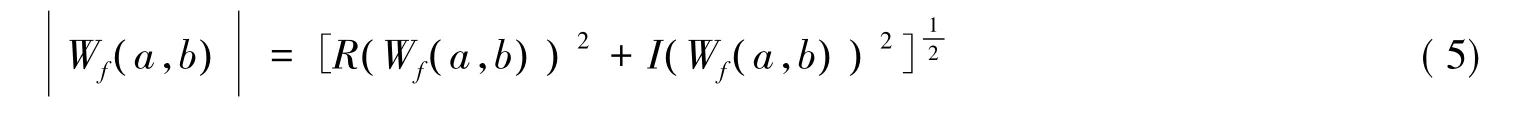
式中：R——取实部；I——取虚部。

定义f( t )的小波谱为

其单位为m2［15］。

图3给出了某人造信号的时间历程，横坐标表示时间，纵坐标表示振幅，通过小波变换得到如图4所示的小波能谱，谱能量S标识单位为m2s2。由图4可以看出，在t＝0～82 s存在频率f＝3.3 Hz的能量分布；t＝20～82s存在f＝0.6 Hz的能量分布；t＝40～82s存在f＝1.2 Hz的能量分布。由此看出小波分析的优点，它能够把时间、频率同时局部化，具有良好的时频分析特性。可见利用小波变换能够对信号进行特征提取和时频特性分析。

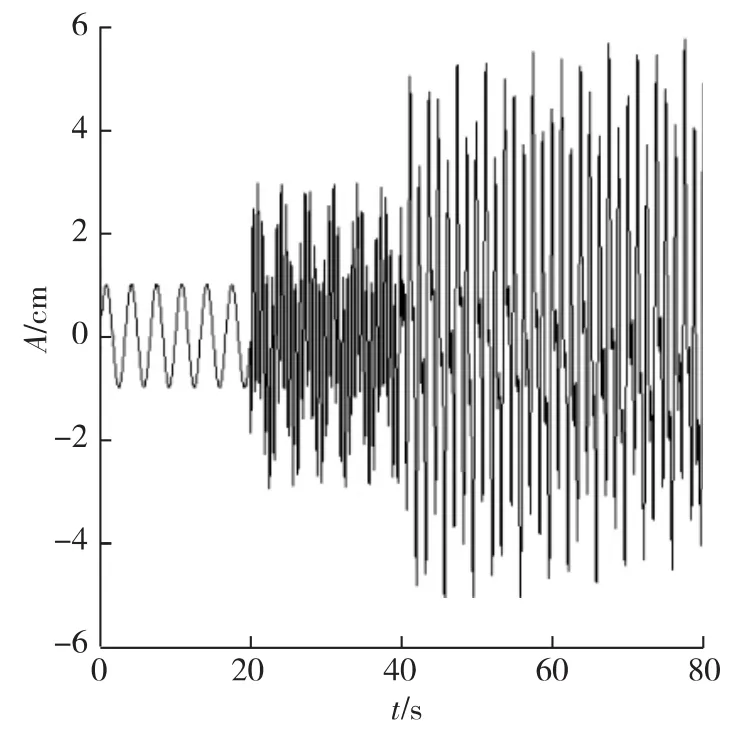
图3　人造信号的时间历程Fig.3 Time history of artificial signal

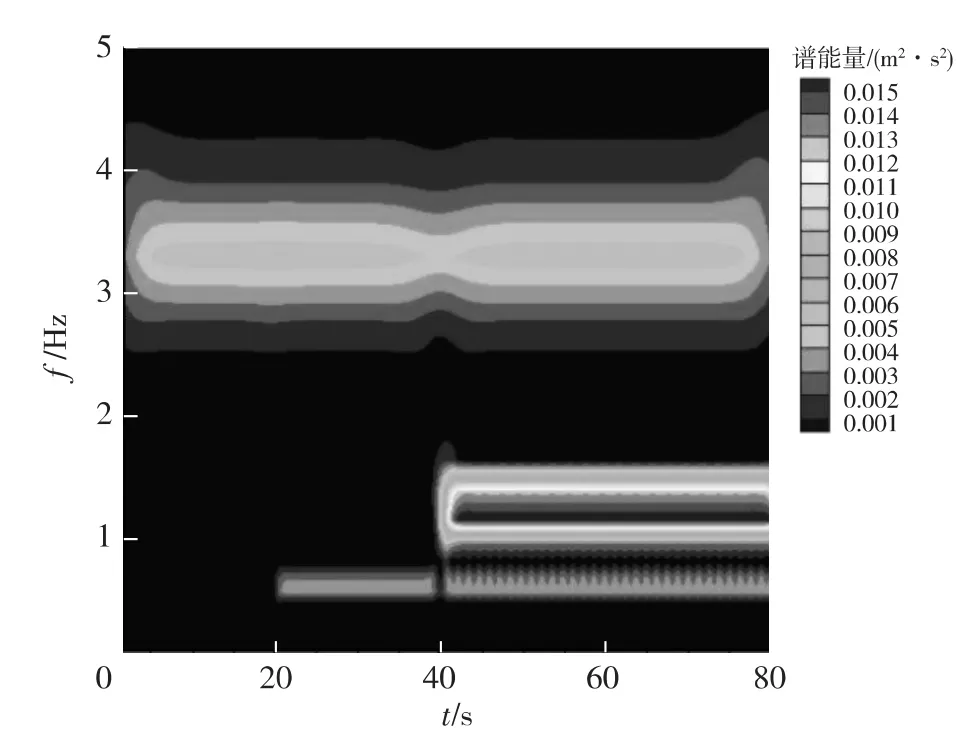
图4　小波能谱Fig.4 Wavelet spectrum

3　剪切不稳定理论

剪切不稳定模式采用Putrevu等［16］推导的计算模型，该模型采用了“刚盖”假定、流场内水平流速由稳定的沿岸流流速场和扰动流速组成的假定，并引入流函数，形式如下：

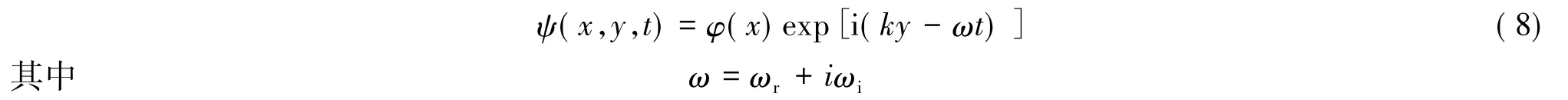
式中：φ（x）——流函数的幅值；k——波数；ωr——沿岸流波动的圆频率；ωi——剪切波的增长率。最后得到沿岸流波动模式模型：

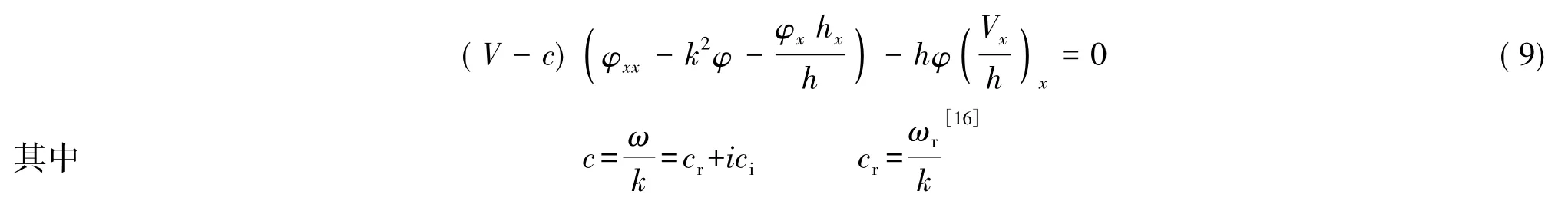
式中：cr——剪切波的相速度。其他变量意义见文献［11］、［16］。

剪切不稳定引起的扰动速度场（u'，v'）参见文献［11］，由扰动速度场可知扰动流速与时间t有关，时间越长扰动速度（u'，v'）越大，而剪切波的发展需要一个时间过程。

4　剪切波时空变化分析

4.1数据预处理

规则波采集时间：1∶100坡180s，1∶40坡240 s。对剪切波进行小波谱分析前要先进行数据预处理［11］，主要包括截取数据、中心化和消除趋势项。由图2可知1∶100坡（波况6）的剪切波在约50s后产生，1∶40坡（波况13）的剪切波在约100s后产生。因此，将规则波1∶100坡的采集时间历程前50s截去，将规则波1∶40坡的采集时间历程前100s截去。趋势项［17-18］是振动信号周期大于记录长度的频率成分，它的存在会使相关分析产生较大误差，所以在测试信号的频域分析中通常要消除趋势项。趋势项分为线性和非线性，而实际应用中趋势项大多数都是非线性的。在一般应用中，如果对信号精度要求不高，常使用线性趋势项来代替。如果需要对信号进行高精度分析，则必须使用非线性趋势项以达到很好的趋势项消除效果。本文使用线性趋势项来代替趋势项。

图5给出了不消除趋势项与消除趋势项的小波能谱。由图5（a）可以看出，由于趋势项的干扰（主要表现为T＝105s尺度的能量分布），使得剪切波的小波谱能量分布几乎失去真实性，影响对剪切波时空变化的研究。图5（b）消除趋势项后仍然存在T＝105s尺度的能量分布，这是由于线性趋势项消除精度不高所致，但已满足试验分析的需要。

图5　不消除趋势项和消除趋势项的小波谱（x＝10m）Fig.5 Wavelet spectrums with and without trend elimination

4.2剪切波时空变化分析

图6给出了对应图2（a）和（b）的小波谱，谱能量S的标识单位为m2，横坐标表示时间t（单位s），纵坐标表示周期T（单位s），表示谱能量，单位为m2小波能量谱反映了局部时-频域上信号能量的大小。基于物理模型试验，利用小波能量谱分析剪切波产生后的时空变化。

由图6（a）可知，随着x的增大，在u方向和v方向上始终存在着T＝105s和T＝2.5s这2个尺度的能量分布。T＝105s尺度的能量分布是由线性消除趋势项精度不高、信号采集长度较短造成的。T＝2.5 s尺度的能量分布由入射波引起，由于入射波是规则波，所以当远离破波带时T＝2.5 s尺度的能量分布呈现出连续性。u方向上，在x＝3～10 m之间的小波谱主要存在着T＝65 s尺度的能量分布；v方向上，在x＝3 m、4 m、6.5m、10m、12m处主要存在着T＝75s尺度的能量分布。

对于剪切波随时间的变化，从图6（a）可以看出，在u和v这2个方向整个时间轴上剪切波都存在连续的能量分布。但随着x增大，2个方向上的剪切波能量最大值都呈先增大、后减小的趋势：u方向为0.26m2—0.32m2—0.6m2—0.38m2—0.2m2，v方向为0.28m2—0.3m2—0.32m2—0.08m2—0.025m2。

对于剪切波随空间的变化，从图6（a）可以看出，在u方向上随着x的增大，剪切波获得最大能量（即剪切波能量分布随时间变化的中心）的时间变化为50 s—40 s—60 s—65 s—80 s，在v方向上是从60 s—65 s—66s—45s—5 s。这种变化趋势是由试验测量的时间历程相对较短、剪切波没有充分发展起来所致。但是可以看出剪切波在破波带附近表现得更明显。另外，u方向上，在x＝3m、4m、9m处还存在着T＝25s尺度的能量分布，v方向上在x＝4m和x＝9m处还存在着T＝35s尺度的能量分布，这种尺度与边缘波的周期特征更加接近［19］。

图6（b）给出了波况13的小波谱，其T＝105s和T＝2.5 s尺度的能量分布与波况6的分析一致。从图6（b）可以看出，v方向上主要存在T＝50s尺度的能量分布，而且v方向上的能量分布比u方向上的更加充分，说明观测到的剪切波主要集中在沿岸方向上。因此主要从沿岸方向分析剪切波的时空变化。

对于剪切波随时间的变化，从6（b）可以看出，除x＝6.5m外，其余各处在整个时间轴上剪切波都存在连续的能量分布。但随着x增大，剪切波能量最大值变化为0.035 m2—0.26 m2—0.38 m2—0.05 m2—0.02 m2，这种趋势与时均沿致，说明剪切波在破波带附近表现得更明显。

对于剪切波随空间的变化，从6（b）可以看出，在x＝2～5.5m处，随着x的增大，剪切波获得最大能量的时间有提前的趋势，从50s—45s—35s—80s—70s。这一方面是因为剪切波主要是由剪切力Vx引起［9］，在不同位置处剪切波所获得的Vx不同；另一方面是由于试验测量的时间历程相对较短，使得剪切波没有充分发展起来。在x＝6.5m处，只存在T＝2.5s尺度的能量分布，这是由于远离了破波带后入射波的作用开始变得明显。

图6　波况6、波况13对应图2的小波谱Fig.6 Wavelet spectrum of case 6 and case 13 corresponding to Fig.2

4.3不同水动力条件下剪切波的变化特性

对于不同地形、不同水动力条件下剪切波的变化特性，选取入射条件（主要指入射波高）［11］不同的波况6（波高4.5cm）和波况12（波高13.0cm）进行分析。受篇幅所限，没有给出波况12的小波能谱，但是其分析结果与波况6、13的基本一致。对于剪切波随时间的变化，与波况6相比，剪切波能量最大值产生的时间相对延后；对于剪切波随空间的变化，与波况6相比，剪切波产生的区域减小。

除上述波况外，对其他波况也做了近似的分析，结果与波况6和波况13基本一致。

5　结　　语

通过对不同波况下的小波谱进行分析，得出以下结论：（a）在入射波为规则波，地形为平直斜坡情况下也可以观测到剪切波。（b）剪切波产生后随时间的变化呈现连续性，但随着距岸线距离的增加，剪切波能量最大值的变化与时均沿岸流的分布基本吻合，而且观察到剪切波在沿岸方向的能量谱中比垂直岸线方向占优势。（c）考虑地形的影响，无论是在相同水动力条件下还是在不同水动力条件下，地形坡度增加都使得剪切波产生的区域减小。（d）无论是规则波1∶40坡还是1∶100坡，由剪切不稳定引起的剪切波频率都在约0.015 Hz（约为65s）左右变化。观测结果一方面可能是由近岸复杂的水动力环境引起，另一方面可能是由于试验测量的时间历程较短，使得剪切波还没有充分发展起来，以至于没有观测到明显的变化特征。

参考文献：

［1］张庆杰.沿岸流不稳定运动对物质输移的影响［D］.大连：大连理工大学，2007.

［2］任春平，邹志利.沿岸流不稳定运动研究进展［J］.海洋通报，2010，29（5）：588-589.（REN Chunping，ZOU Zhili.Research development of the shear instability of longshore currents［J］.Marine Science Bulletin，2010，29（5）：588-589.（in Chinese））

［3］OLTMAN-SHAY J，HOWD P A，BIRKEMEIER W A.Shear instabilities of The mean longshore current 2.field observations［J］.Journal of Geophysical Research，1989，94（C12）：18031-18042.

［4］RENIERS A，BATTJES J A，FALQUES A，et al.A laboratory study on the shear instability of longshore currents［J］.Journal of Geophysical Research，1997，102（C4）：8597-8609.

［5］RENIERS A，BATTJES J A.A laboratory study of longshore currents over barred and non-barred beaches［J］.Coastal Engineering，1997，30（1）：1-21.

［6］NOYES T J，GUZA R T，ELGAR S，et al.Field observations of shear waves in the surf zone［J］.Journal of Geophysical Research，2004，109（C0）：1031.

［7］邹志利，任春平，金红，等.沿岸流不稳定性运动试验研究［C］//佚名.第十二届中国海岸工程会议论文集.北京：海洋出版社，2005：334-338.

［8］金红，邹志利，邱大洪，等.波生流对海岸污染物输移的影响［J］.海洋学报，2006，28（6）：144-150.（JING Hong，ZOU Zhili，QIU Dahong，et al.The effects of wave-induced currents on the transport of pollutant outside and inside surf zone［J］.Acta Oceanologica Sinica，2006，28（6）：144-150.（in Chinese））

［9］任春平，蒋利君，邹志利.不规则波致沿岸流不稳定运动时空变化研究［J］.应用基础与工程科学学报，2012，20（6）：1099-1109.（REN Chunping，JIANG Lijun，ZOU Zhili.Variation of instabilities of irregular waves induced longshore currents in time and spatial domain［J］.Journal of Basic Science and Engineering，2012，20（6）：1099-1109.（in Chinese））

［10］BOWEN A J，HOLMAN R A.Shear instabilities of the mean longshore current 1：theory［J］.Journal of Geophysical Research，1989，94（C12）：18023-18030.

［11］任春平.沿岸流不稳定运动的试验研究及理论分析［D］.大连：大连理工大学，2009

［12］王文圣，丁晶，李跃清.水文小波分析［M］.北京：化学工业出版社，2005：3-26.

［13］李响，颜冰.小波谱在船舰地震波场分析中的应用［J］.振动与冲击，2008，27（4）：156-158.（LI Xiang，YAN Bing.Application of wavelet spectrum and wavelet coherence in ship's seism IC-wave field［J］.Journal of Vibration and Shock，2008，27（4）：156-158.（in Chinese））

［14］李强，王其申.小波谱及其在线性调频信号检测中的应用［J］.量子电子学报，2005，22（5）：686-689.（LI Qiang，WANG Qishen.Wavelet spectrum and its application to LFM signal detection［J］.Chinese Journal of Quantum Electronics，2005，22（5）：686-689.（in Chinese））

［15］TORRENCE C，COMPO G T P.A practical guide to wavelet analysis［J］.Bulletin of the American Meteorological Society，1998，79（1）：61-78.

［16］PUTREVU U，SVENDSEN I A.Shear instability of longshore currents：a numerical study［J］.Journal of Geophysical Research，1992，97（C5）：7283-7303.

［17］王广斌，刘义伦，金晓宏，等.基于最小二乘原理的趋势项处理及其MATLAB的实现［J］.有色设备，2004（5）：4-8.（WANG Guangbin，LIU Yilun，JIN Xiaohong，et al.Treatment of tendency part and its MATLAB accomplishment based on Least-Square principle［J］.Non-Ferrous Metallurgical Equipment，2004（5）：4-8.（in Chinese））

［18］高品贤.趋势项对时域参数识别的影响及消除［J］.振动、测试与诊断，1994，14（2）：21-26.（GAO Pingxian.Effect and removal of trends on parameters identification in time doman［J］.Journal of Vibration，Measurement＆Diagnosis，1994，14（2）：21-26.（in Chinese））

［19］GUZA R T.Laboratory simulation of edge wave［J］.Coastal Engineering，1997，16（1）：64-70.

Temporal and spatial variations of shear waves under regular waves

JI Haijia1，REN Chunping1，2，JIANG Lijun1
（1.College of Water Conservancy Science and Engineering，Taiyuan University of Technology，Taiyuan 030024，China；2.State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China）

Abstract：Based on a physical model experiment，the wavelet transform theory，and shear instability theory，temporal and spatial variation characteristics of shear waves were investigated under the conditions that the incident waves were regular waves and the topography was a flat slope.By analyzing the wavelet energy spectrum of the shear wave velocity time history under 15 wave conditions，results can be obtained and show that when the incident waves are regular waves and the topography is a flat slope，shear waves can be observed but the temporal and spatial variations are not significant；the variation of shear waves over time is continuous once it has been generated；shear waves are more dominant in the energy spectrum in the direction along the bank than in the spectrum vertical to the shoreline；an increase in the slope will reduce the generated area of shear waves；and the shear wave frequency，caused by the shear instability，changes around 0.015 Hz with a of gradient of 1∶40 or a gradient of 1∶100.

Key words：temporal and spatial variations of shear wave；regular wave；wavelet transform theory；shear instability theory；wavelet spectrum

通信作者：任春平，副教授。E-mail：chunpingren@163.com

作者简介：季海嘉（1988—），男，山西朔州人，硕士研究生，主要从事海岸水动力学研究。E-mail：jihaijiamv@sina.com

基金项目：中国博士后面上基金（2013M541179）；水利工程仿真与安全国家重点实验开放基金（HESS-1406）

收稿日期：2014-12-26

DOI：10.3876/j.issn.1000-1980.2016.01.009

中图分类号：P731.21

文献标志码：A

文章编号：1000-1980（2016）01-0051-07