基于对数线性流速分布的含沙量垂线分布

赵树林，诸裕良，邵宇阳（.河海大学港口海岸与近海工程学院，江苏南京　20098；2.浙江省电力设计院，浙江杭州　3002）



基于对数线性流速分布的含沙量垂线分布

赵树林1，2，诸裕良1，邵宇阳1
（1.河海大学港口海岸与近海工程学院，江苏南京210098；2.浙江省电力设计院，浙江杭州310012）

摘要：为解决河口海岸地区非恒定流条件下的流速剖面常偏离传统的对数流速分布问题，以对数线性流速分布为基础，推导出动量交换系数，并基于扩散理论得出含沙量垂线分布公式。利用长江口及杭州湾金山海域各层含沙量实测资料对含沙量垂线分布公式进行验证，结果表明，该公式不仅克服了Rouse公式表面水体含沙量为零的缺点，而且在整个水深上与实测含沙量吻合得更好，能够较好地反映河口海岸地区含沙量垂线分布特征。

关键词：对数线性模式；动量交换系数；扩散理论；含沙量垂线分布；长江口；杭州湾金山海域

悬移质含沙量垂线分布是泥沙研究的重要基础之一，其与污染物扩散、泥沙输运、岸滩演变、底床冲淤等问题密切相关。但是由于悬移质含沙量垂线分布的内在物理机理很复杂，因此目前尚未得到完善解决。河口海岸海域受风浪、潮流等多种复杂因子的影响，因此其含沙量垂线分布比河流中复杂。

目前，研究含沙量垂线分布的理论主要包括扩散理论、混合理论、能量理论、相似理论、随机理论和有限掺混长度理论等，其中应用最广泛的是扩散理论。众多学者基于不同的研究角度，得到多种含沙量垂线分布公式。Rouse［1］首先引入扩散理论，推导出悬移质泥沙浓度分布公式，开创了理论研究的先河；van Rijn［2-3］、钱宁等［4］、张瑞瑾［5］也为扩散理论做出了突出贡献，分别得出了含沙量的垂线分布公式；维利卡诺夫从能量平衡原理出发首创了重力理论，考虑了泥沙悬浮对水流的影响，得出悬移质含沙量的垂线分布［4］；Mctigue［6］假设流体和分散的悬浮固体颗粒可分别视为连续介质，得到了一个对应于分层模式的运动方程，从动力学上解释了扩散理论；蔡树棠［7］仿照涡量相似理论，得到了挟沙水流挟带泥沙的涡量涨落所满足的方程式，推导出悬沙分布公式；倪晋仁等［8］基于泥沙悬浮特征长度推导出含沙量垂线分布的统一公式；刘大有［9］基于二相流的双流体模型得到明渠含沙量垂线分布公式；Nielsen等［10］根据有限掺混长度理论得出含沙量垂线分布公式；Brown［11］假设垂向不平衡输沙完全由对流输运引起，提出了悬沙剖面的计算方法；此外，还有一些学者［12-21］也对含沙量分布作了一些研究，得出含沙量垂线分布公式。

倪晋仁等［22］从理论上揭示了采用扩散理论、能量理论、混合理论、相似理论及随机理论在求解悬移质浓度分布公式时都能归化为扩散方程的简单形式，主要的差别是泥沙扩散系数有所不同。因此，采用扩散理论研究含沙量垂线分布规律是合理的，此时求解一维扩散方程的关键是如何确定合理的泥沙扩散系数εs。通常认为εs与流体湍流扩散系数或动量交换系数相当，很大程度上受水流的垂直结构，尤其是近底水流的垂直结构及其相应的底床剪切应力的影响。在非恒定流条件下，尤其是河口海岸地区，水体呈往复流动，且风、波浪等外界动力因素的扰动较强，传统的对数流速分布模式不再适用。Soulsby等［23］指出在加速潮流中近底流速剖面偏离常用的对数流速剖面，通过引入加速长度得到新的流速分布。Kuo等［24］通过理论分析，得出了非恒定潮流模型底部剪切力边界条件的公式，使用常规摄动法求解非恒定流边界层方程得出临近边界层的对数线性流速分布。但Soulsby等［23］、Kuo等［24］引入的加速长度和摄动量缺乏明确的物理意义。Song等［25］、郝嘉凌等［26］利用Prandtl混合长度和von Karman自相似理论，建立了河口海岸近底层水流结构的对数线性流速分布和对数线性扩展流速分布模式，此对数线性流速分布更适用于河口海岸水域。本文以对数线性流速分布［25］为基础，推导出含沙量垂线分布公式。

1　含沙量垂线分布公式推导

1.1动量交换系数

对于二元恒定均匀流，根据掺混长度理论可得

式中：τ——水流紊动切应力（忽略黏性切应力）；ρ——清水密度；l——水体掺混长度；u——水流时均流速；y——垂向坐标；εm——动量交换系数。

研究表明，明渠流中无论是清水还是挟沙水流，紊动切应力都基本呈线性分布：

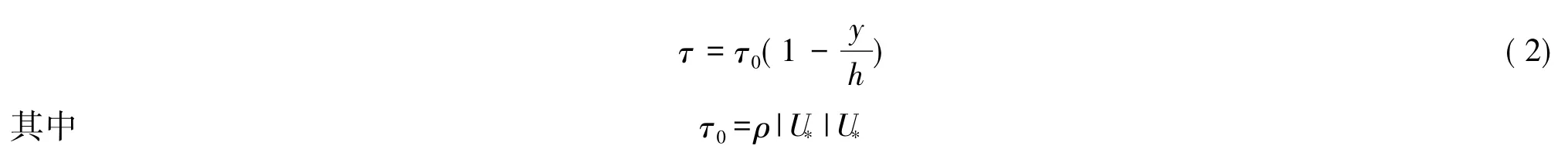
式中：τ0——作用在床面上的水流切应力；h——水深；U*——摩阻流速。

由式（1）、式（2）可得

她从头到尾见证了他们被屠杀的过程。人的残忍真是没有极限，没有止境。天下是没有公理的，否则一群人怎么跑到别人的国家如此撒野?把别人国家的人如此欺负?她哭还因为自己国家的人就这样软弱，从来都是受人欺负。书娟哭得那个痛啊，把冲天冤屈都要哭出来。

本文采用对数线性流速公式［21］：

式中：κ——卡门常数；y0——粗糙长度；C——参数，取决于水流结构。

选取长江口1号、2号测点大潮各层流速实测资料来验证式（4）及对数流速分布在河口海岸的适用性（其他测点结果相似），结果见图1（纵坐标η＝y/h）。其中，长江口1号测点坐标为（122°23' 10.08″E，31°07'14.13″N），2号测点坐标为（121°52'48.05″E，31°16'57.06″N），测量时间为2009年4月28日0：00-5：00。

图1　长江口1号、2号测点流速垂线分布Fig.1 Vertical distribution of velocity at No.1 and No.2 stations in Yangtze Estuary

从图1可以看出，多数情况下流速垂线分布偏离传统的对数流速分布，而与对数线性流速分布更为吻合。因此，笔者基于式（4）推导含沙量垂线分布是合理的。

对式（4）求导得

将式（5）代入式（3）得

将式（5）、式（6）代入εm表达式可得

将式（8）与Rouse公式、van Rijn公式的动量交换系数与Vanoni实测数据进行对比，如图2所示。由图2可知，Rouse公式采用的动量交换系数与实测数据在近底层吻合，但在中层以上出现差异；van Rijn公式采用的动量交换系数在近底层至中层与Rouse公式一致，但越接近表层其差异越大。式（8）较合理地反映了动量交换系数随水深的变化，与实测数据更吻合。因此，本文采用对数线性流速分布推导出的动量交换系数分布更合理。

1.2含沙量垂线分布

二维泥沙扩散方程为

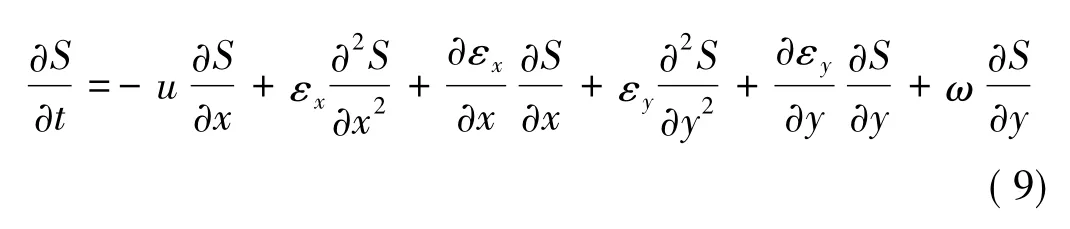
式中：S——含沙量（体积比）；ω——泥沙沉速；εx、εy——沿水流方向及与水流垂直方向的泥沙扩散系数。

当悬移质含沙量垂线分布达到平衡状态时，泥沙扩散问题成为一个均匀、恒定的问题，式（9）中对距离x和时间t的偏微分项均等于零，式（9）简化为

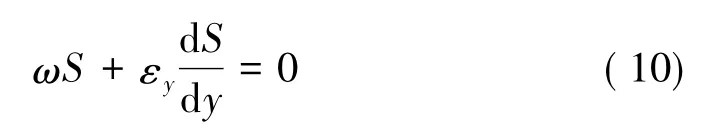
由于εy与εm尚无明确关系，且其差异很小，这里假设εy＝εm，将式（8）代入式（10）中并积分，设参考点y＝a处的含沙量为Sa，可得含沙量垂线分布规律为

式中：z——悬浮指标。

图2　式（8）和Rouse公式、van Rijn公式的动量交换系数与Vanoni实测数据对比Fig.2 Comparison of momentum exchange coefficients from Eq.（8），Rouse equation，and van Rijn equation with measured data obtained by Vanoni

2　实测资料验证分析

选取长江口及杭州湾金山海域大潮各层含沙量实测资料对式（11）进行验证，结果见图3～4。长江口测点含沙量的测量时间为2009年4月28日0：00～5：00，1号、2号测点坐标与前文相同；金山海域测点含沙量的测量时间为2011年9月29日4：00～9：00，1号测点坐标为（121°32'01.41″E，30°44'51.50″N），2号测点坐标为（121°23'42.20″E，30°41'55.77″N）。为更好地体现式（11）的精度，并鉴于Rouse公式在实际工程计算中应用广泛，在将式（11）的计算值与实测值进行比较的同时，引入Rouse公式的计算结果共同比较（取a＝0.05h）。

图3　长江口1号、2号测点大潮含沙量垂线分布Fig.3 Vertical distribution of sediment concentration during spring tide at No.1 and No.2 stations in Yangtze Estuary

由图3～4可以看出，Rouse公式计算结果在中层及底层与实测含沙量基本吻合，但当表层含沙量不为零时，Rouse公式上层计算结果与实测含沙量偏差较大。式（11）的计算结果在上层要明显优于Rouse公式，且很多时间里在中、下层也是优于Rouse公式的。从整个垂线分布看，式（11）的计算结果与实测数据吻合得更好，而且克服了Rouse公式水面处含沙量为零的缺点。总体上说，式（11）比Rouse方程更加合理地反映了整个水深的含沙量垂线分布规律。

但当含沙量垂线分布极不规律，如图3（a）中1：00时刻出现的S形，式（11）和Rouse公式都不能很好地反映实测含沙量垂线分布规律。这可能由涨落潮交替、盐淡水混合等多种因素造成，有待进一步研究。尽管如此，式（11）的计算结果还是比Rouse公式稍好一点。

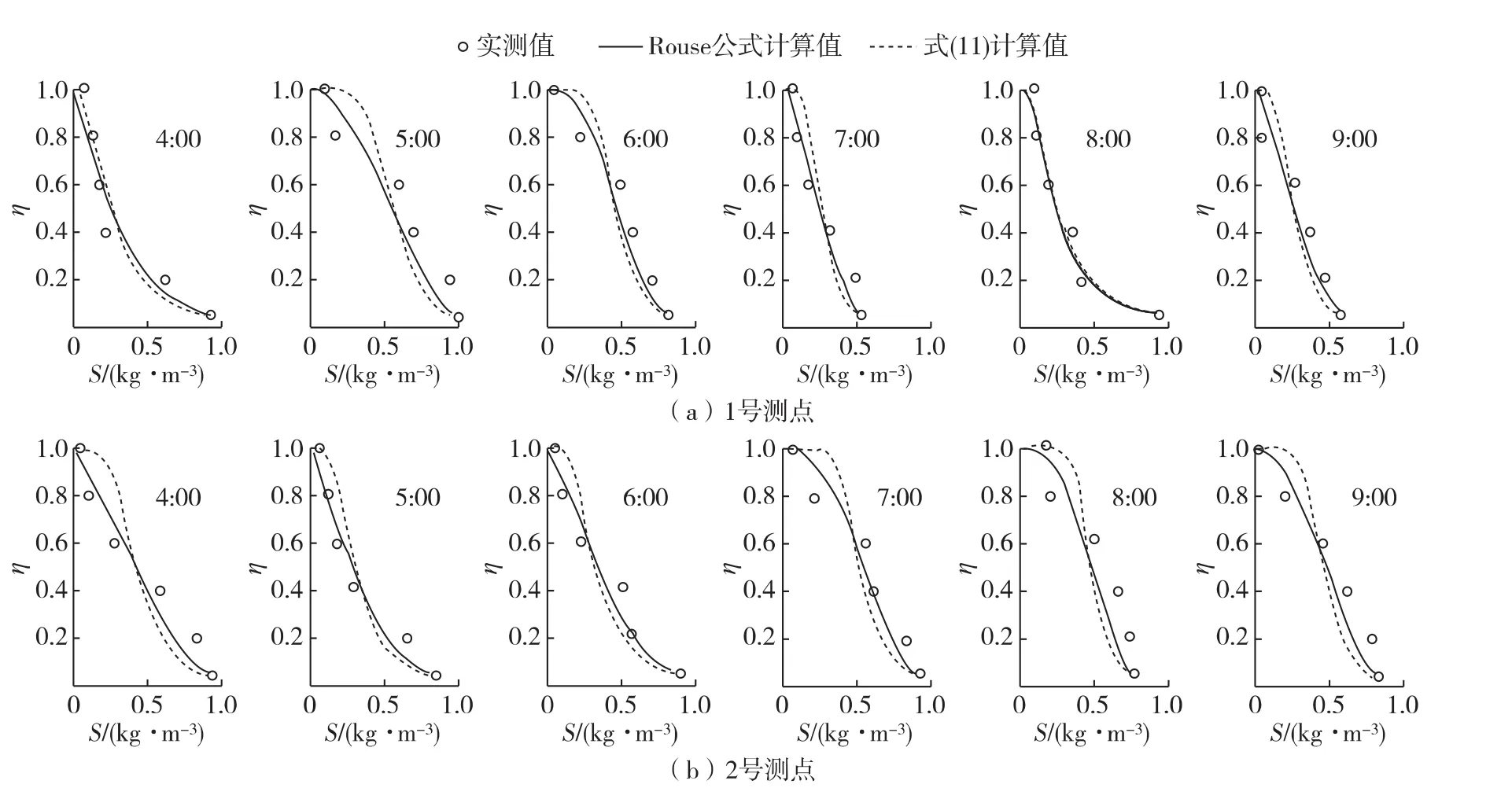
图4　金山海域1号、2号测点大潮含沙量垂线分布Fig.4 Vertical distribution of sediment concentration during spring tide at No.1 and No.2 stations in Jinshan sea area

3　结　　论

a.在非恒定流条件下，尤其是河口海岸地区，流速剖面常偏离传统的对数流速剖面，而对数线性流速分布模式更为适用。

b.以对数线性流速分布为基础推导出的动量交换系数分布，与实测数据吻合程度比前人结果更好。

c.本文含沙量垂线分布公式不仅克服了Rouse公式表面水体含沙量为零的缺点，而且其计算结果在整个垂线上与实测含沙量吻合得更好，能够较好地反映河口海岸地区含沙量垂线分布特征。

参考文献：

［1］ROUSE H.Modem conception of the mechanics of fluid turbulence［J］.Transactions of the American Society of Civil Engineers，1937，102（1）：463-505.

［2］van RIJN L C.Principles of sediment transport in rivers，estuaries and coastal seas［M］.Amsterdam：Aqua Publications，1993.

［3］van RIJN L C.Sediment transport，part II：suspended load transport［J］.Journal of Hydraulic Engineering-ASCE，1984，110 （11）：1613-1641.

［4］钱宁，万兆惠.泥沙运动力学［M］.北京：科学出版社，1983.

［5］张瑞瑾.河流泥沙动力学［M］.北京：水利电力出版社，1989.

［6］MCTIGUE D F.Mixture theory for suspended sediment transport［J］.Journal of the Hydraulics Division，1981，107（6）：659-673.

［7］蔡树棠.相似理论和泥沙的垂直分布［J］.应用数学和力学，1982，3（5）：605-612.（CAI Shutang.The theory of similarity and the profile of vertical distribution of concentration of sand particles［J］.Applied Mathematics and Mechanics，1982，3（5）：605-612.（in Chinese））

［8］倪晋仁，王光谦.泥沙悬浮的特征长度和悬移质浓度垂线分布［J］.水动力学研究与进展，1991，7（2）：167-175.（NIJinren，WANG Guangqian.Characteristic length and vertical concentration distribution of suspended sediment［J］.Journal of Hydrodynamics，1991，7（2）：167-175.（in Chinese））

［9］刘大有.从二相流方程出发研究平衡输沙：扩散理论和泥沙扩散系数的讨论［J］.水利学报，1995，26（4）：62-67.（LIU Dayou.A study of sediment transport from the equations of turbulent two-phase flows：a discussion on diffusion theory and diffusion coefficient of sediment［J］.Journal of Hydraulic Engineering，1995，26（4）：62-67.（in Chinese））

［10］NIELSEN P，TEAKLE I A L.Turbulent diffusion of momentum and suspended particles：a finite-mixing-length theory［J］.Physics of Fluids，2004，16（7）：2342-2348.

［11］BROWN G L.Approximate profile for nonequilibrium suspended sediment［J］.Journal of Hydraulic Engineering-ASCE，2008，134（7）：1010-1014.

［12］陈永宽.悬移质含沙量沿垂线分布［J］.泥沙研究，1984（1）：31-40.（CHEN Yongkuan.Vertical distribution of suspended sediment in open channel［J］.Journal of Sediment Research，1984（1）：31-40.（in Chinese））

［13］张小峰，陈志轩.关于悬移质含沙量沿垂线分布的几个问题［J］.水利学报，1990，21（10）：41-48.（ZHANG Xiaofeng，CHEN Zhixuan.On the distribution of sediment concentration［J］.Journal of Hydraulic Engineering，1990，21（10）：41-48.（in Chinese））

［14］曹志先，张效先，习和忠.基于湍流猝发的明渠流悬沙浓度分布［J］.水利学报，1997，28（2）：52-57.（CAO Zhixian，ZHANG Xiaoxian，XI Hezhong.Turbulent bursting-based concentration profiles of suspended sediment in open channel flows［J］.Journal of Hydraulic Engineering，1997，28（2）：52-57.（in Chinese））

［15］严冰，张庆河.基于有限掺混长度概念的悬沙浓度垂线分布研究［J］.泥沙研究，2008（1）：9-16.（YAN Bing，ZHANG Qinghe.Distribution of vertical suspended sediment concentration based on the finite mixing length conception［J］.Journal of Sediment Research，2008（1）：9-16.（in Chinese））

［16］HUANG Huiming，WANG Yigang，WEN Yuncheng，et al.Vertical distribution of momentum exchange coefficient and sediment concentration in estuarine and coastal waters［J］.China Ocean Engineering，2010，24（4）：677-692.

［17］李瑞杰，丰青，郑俊，等.近岸海域流速与含沙量垂线分布分析［J］.海洋通报，2012，31（6）：607-612.（LI Ruijie，FENG Qing，ZHENG Jun，et al.Analysis on vertical distribution of nearshore fluid velocity and sediment concentration［J］.Marine Science Bulletin，2012，31（6）：607-612.（in Chinese））

［18］朱文谨，潘锡山，孙杰.基于Rouse方程的河口海岸水域泥沙垂线浓度分析［J］.河海大学学报（自然科学版）2012，40（2）：215-219.（ZHU Wenjin，PAN Xishan，SUN Jie.Analysis of vertical distribution of sediment concentration in estuarine and coastal water areas based on Rouse equation［J］.Journal of Hohai University（Natural Sciences），2012，40（2）：215-219.（in Chinese））

［19］丰青，李瑞杰，江森汇，等.基于含沙紊动水流掺混长度的含沙量垂线分布［J］.河海大学学报：自然科学版，2012，40（5）：549-554.（FENG Qing，LI Ruijie，JIANG Senhui，et al.Vertical distribution of suspended sediment concentration based onmixing length of sediment-laden turbulent flow［J］.Journal of Hohai University（Natural Sciences），2012，40（5）：549-554.（in Chinese））

［20］郑俊，李瑞杰，丰青，等.近岸悬沙质量浓度垂线分布公式［J］.河海大学学报（自然科学版）2013，41（5）：452-455.（ZHENG Jun，LI Ruijie，FENG Qing，et al.Formula of vertical distribution of nearshore suspended sediment concentration［J］.Journal of Hohai University（Natural Sciences），2013，41（5）：452-455.（in Chinese））

［21］莫磊，李瑞杰，李佳芮，等.悬移质泥沙的垂线分布［J］.河海大学学报（自然科学版）2013，41（1）：90-94.（MO Lei，LI Ruijie，LI Jiarui.Research on vertical distribution of suspended sediment concentration［J］.Journal of Hohai University（Natural Sciences），2013，41（1）：90-94.（in Chinese））

［22］倪晋仁，惠遇甲.悬移质浓度垂线分布的各种理论及其间关系［J］.水利水运科学研究，1988（1）：83-97.（NI Jinren，HUI Yujia.The various theories of suspended load concentration vertical distribution and their relationships［J］.Hydro-Science and Engineering，1988（1）：83-97.（in Chinese））

［23］SOULSBY R L，DYER K R.The form of the near-bed velocity profile in a tidally accelerating flow［J］.Journal of Geophysical Research：Oceans，1981，86（C9）：8067-8074.

［24］KUO A Y，SHEN J，HAMRICK J M.Effect of acceleration on bottom shear stress in tidal estuaries［J］.Journal of Waterway，Port，Coastal，and Ocean Engineering，1996，122（2）：75-83.

［25］SONG Zhiyao，YAN Yixin，HAO Jialing，et al.Study on the log-linear velocity profile of near-bed tidal current in estuarine and coastal waters［J］.China Ocean Engineering，2006，20（4）：573-584.

［26］郝嘉凌，宋志尧，严以新，等.河口海岸潮流速分布模式研究［J］.泥沙研究，2007（4）：34-41.（HAO Jialing，SONG Zhiyao，YAN Yixin，et al.Study on the tidal velocity profile in the estuarine and coastal areas［J］.Journal of Sediment Research，2007（4）：34-41.（in Chinese））

Vertical distribution of sediment concentration based on log-linear velocity distribution

ZHAO Shulin1，2，ZHU Yuliang1，SHAO Yuyang1
（1.College of Harbor，Coastal and Offshore Engineering，Hohai University，Nanjing 210098，China；2.Zhejiang Electric Power Design Institute，Hangzhou 310012，China）

Abstract：In order to solve the problem of velocity profiles in estuarine and coastal areas often deviating from the traditional logarithmic velocity distribution，a momentum exchange coefficient is derived based on log-linear velocity distribution，and an equation describing the vertical distribution of sediment concentration is established based on the diffusion theory.Through validation using measured data regarding vertical stratified sediment concentration in the Yangtze Estuary and Jinshan sea area in Hangzhou Bay，it is found that the new equation describing the vertical distribution of sediment concentration not only overcomes the Rouse equation defect of the surface sediment concentration being zero，but also agrees with the measured sediment concentration along the vertical line，indicating that the equation objectively reflects the vertical distribution rule of sediment concentration in estuary and coastal areas.

Key words：log-linear distribution；momentum exchange coefficient；diffusion theory；vertical distribution of sediment concentration；Yangtze Estuary；Jinshan sea area in Hangzhou Bay

通信作者：诸裕良，教授。E-mail：zhuyl@hhu.edu.cn

作者简介：赵树林（1989—），男，山东烟台人，硕士研究生，主要从事河口海岸动力学研究。E-mail：zhaoshuln@163.com

基金项目：国家自然科学基金重点项目（51339005）；国家自然科学基金青年项目（51409081）；交通部河口海岸交通行业重点实验室开放课题（2010CB429000）

收稿日期：2014-09-03

DOI：10.3876/j.issn.1000-1980.2016.01.008

中图分类号：TV149

文献标志码：A

文章编号：1000-1980（2016）01-0045-06