将“类比”进行到底

周旋

分式知识对初中生是一个既熟悉又陌生的知识，说熟悉，因为学生认知中已有分数的知识储备，且在学习整式时有过浅显的比较；说陌生，因为学生对其表现形式并不清楚。因此本节课承担着由分数向分式过渡的重要任务。

备课时教师首先应思考的是如何设定教学目标，三维目标不是割裂的，而是一个有机整体，即过程与方法、情感态度与价值观的目标是依靠知识与技能的教学达成的，是在知识与技能的教学过程中逐步渗透的。笔者设置了如下教学目标。

知识与技能：一是了解分式的概念。

二是能确定分式有意义和分式值为0的条件。

过程与方法：一是经历从具体情境抽象出分式的过程，体会分式是反应现实问题的一种数学模型。

二是在探究分式概念的过程中，体会运用类比研究问题的思想方法。

情感态度与价值观：借助观察、归纳、类比等活动，在独立思考的基础上，积极参与讨论，敢于发表意见，体会合作的乐趣。

一、教学的引入及概念的形成

1.教学的引入

教学引入需要情境，对于本节课，情境的创设既要吸引学生眼球，又要与具体教学内容相结合；既要基于学生已有对分数的认知，又要将学生带入到分式这个新领域中，引发学生思考。笔者设置了如下的问题情境。

教师出示北京市朝阳区地图，标记两个位置，根据此情形设计相关教学问题。

（1）家到学校的路程是10km，如果骑自行车需3h，则骑车速度应该记多少km/h？如果步行需7 h，则步行速度应该记多少km/h？

（2）如果家到学校的路程为s，骑车所用时间为2 h，则车速为多少？

（3）如果家到学校的路程为s，骑车所用时间为t，则车速为多少？若步行所用时间比骑车多2 h，则步行速度为多少？

（4） 如果家到学校的路程为8km，步行所用时间为t，则速度为多少？

上述情境贴近学生生活，吸引学生，同时问题简单易懂，学生乐于参与其中，通过独立思考就得出了答案，分别是 。这样的问题情境，唤起学生的认知，为分式概念的提出作了铺垫。

2.概念的形成及理解

首先，学生通过观察，找出 是熟悉的分数，同时发现其它式子的异同，教师通过提问给予提示：类比分数，其它式子有哪些相同点和不同点？

然后，学生分小组进行讨论，在类比中寻找相同和不同之处，在类比中形成了分式的概念。在笔者的教学实践中，学生充分探讨后，小组汇报，互相补充，得出了分式是形如 且 中含有字母，但没有得出 中都含有字母這一条件，于是笔者通过引导学生类比分数的分子分母，发现它们都是整数，进一步得出分式的分子分母应都为整式，从而形成了完整的分式概念。

此外，笔者在教学中加入了学生独立创编分式、小组内检验的环节，学生热情高涨，编出很多形式的代数式，其中包含分式，也有整式，更有如 形式的分式，有同学提出质疑，最终小组同学提出了两种方法辨析，第一种方法是通过类比 ，虽能约分，但它是分数；第二种方法是通过分式定义得出了正确结论。这一环节在笔者的教学中是亮点，学生参与度高，虽然暴露出问题，但正好创造了理解分式概念的机会，同时学生各抒己见，激发了学生思考和表达的欲望，更能体现出类比学习的优势。。

二、分式有意义及分式值为0的条件

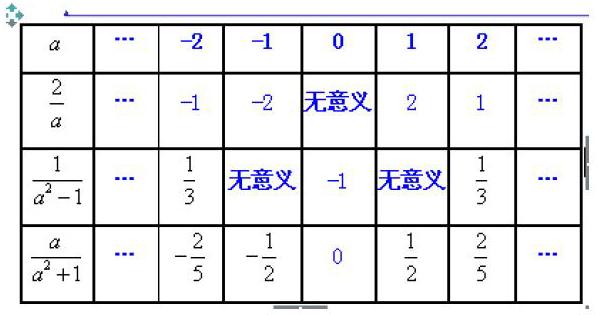
分式的形式与分数有相同之处，分式是将分数抽象化的结果，更能代表一般的分数。分式有意义的条件，即分母不为0；分式值为0的条件，即分母不为0且分子为0，是本节课教学的重点，更是学生对分式深入理解的重要部分。为了更明确的类比分数与分式，让学生深刻体会到分数向分式的过渡，笔者设计了一个表格进行教学。

教学中，除了3个填写无意义的空格，学生都能顺利完成，对于这3个格子，有的同学填写了0，我只是微笑。这时候，小组同学就开始疑惑并分析，比如 ，有同学说，当 时，这个分式就是 的意思，除数不能为0，所以这里 ；受他的启发，其余同学也纷纷重新思考其余空格是否正确。学生显然已经自发地将分式与分数进行类比学习，而正是表格为学生提供了这个机会。这种在类比中追根溯源解决问题的方法，既为学生提供了一种解决问题的办法，同时培养了学生合作的精神。

在学生充分研究讨论的基础上，教师经提炼总结，得出上述条件并板书。

三、巩固练习及课堂小结

巩固练习是对本节数学知识的深化，判断分式有意义及分式值为0的条件时分式学习中的重要习题，而且会联系其他知识。如 有意义的条件， 值为0的条件等，这里不再赘述。

对于课堂小结，除了知识点的梳理，更值得一提的是学习新知识的方法——类比，当遇到新知识，类比着熟悉的知识去学习去探索的方法，是初中数学非常常用的方法。在本节课的教学点滴中渗透给学生，更是为学生接下来学习分式运算等提供了基础，为学习其它知识提供了方法。

分式是初中数学中一个浅显的知识，但其中蕴含的类比的思想方法是深刻的，在本节数学教学中，应将类比的方法进行到底，使得处处有类比，处处有体会。这样不仅是对学生学习方法的指引，更提升了我们的数学教学的高度。