分数跳-扩散模型下具有交易费用的回望期权定价研究

王伟伟，韩　松（南京财经大学应用数学学院，江苏南京210046）



分数跳-扩散模型下具有交易费用的回望期权定价研究

王伟伟，韩松
（南京财经大学应用数学学院，江苏南京210046）

摘要：B-S模型成功解决了完全市场下欧式期权的定价问题.文章主要研究不完全市场下标的资产股票价格服从分数跳-扩散过程且具有交易费用的回望期权定价问题.利用无套利原理和证券组合技术，建立回望期权定价模型，并依此模型给出分数跳-扩散过程下具有交易费用的回望期权定价公式，推广已有的回望期权定价理论.

关键词：回望期权；分数跳-扩散模型；交易费用

近年来，国际金融衍生市场除交易人们广为熟悉的欧式、美式期权外，还涌现了大量由标准期权变化、组合及派生出的新品种，即新型期权，它们是由金融机构设计以满足市场特殊需求的产品.回望期权就是其中比较典型的新型期权，且又是强路径依赖型期权，它的收益依赖于整个“回望期”内的标的资产价格，期权持有者按照“买进按低价，卖出按高价”的原则进行投资.由于这类期权收益较高，所以价格十分昂贵.相对于欧式期权，回望期权价格涉及到价格路径，所以其定价要复杂得多.

对于回望期权的定价研究，文［1］利用修正的二叉树方法来研究货币回望期权.文［2］利用Fourier变换方法求出了带一般收益函数的欧式回望期权的定价公式.文［3］研究了利率为随机情况下的回望期权定价公式.钱丽丽等［4］讨论了标的资产价格服从标准布朗运动下具有交易费用的回望期权定价问题，并给出了回望期权的定价公式.为克服标准布朗运动不能完全反映股票价格变化过程的缺陷，孙玉东等［5］研究了分数跳-扩散过程下回望期权的定价.左岭等［6］在标的资产价格遵循跳跃扩散过程的假设下，运用风险中性定价法和Edgeworth级数逼近及条件期望等相关知识，推导出以离散算术平均资产为浮动执行价的回望买入期权的价格公式.

本文则在考虑交易费的基础上，结合分数跳-扩散模型，建立了分数跳-扩散过程下具有交易费的回望期权定价模型，由于回望期权具有强路径依赖性，推导过程中会添加一个路径因子，我们运用证券组合技术，并对交易时间进行离散化处理，建立了回望期权的定价模型，然后通过波动率修正求解偏微分方程，最终给出了分数跳-扩散模型下具有交易费的回望期权定价公式.

1　回望期权的定价模型

1.1模型假设

（i）允许卖空股票；

（ii）无套利机会；

（iii）标的股价遵循分数跳-扩散过程且具有红利支付，满足以下随机微分方程：

其中，r为无风险利率，q为红利率，σ为波动率，r,q,σ均为常数，为分数布朗运动，为与相互独立且参数为λ的泊松过程，为股价跳跃的相对高度，，且

（iv）投资策略每隔δt时间重新调整一次，且δt相对于T是一个固定，非无穷小的数；

（v）买卖股票需要按股价支付比例交易费κ|| v S，其中v表示股票交易份额，v＞0表示买进，v＜0表示卖出，κ为每单位股价应支付的交易费；

（vi）对冲的投资组合的期望回报率等于无风险利率.

1.2模型推导

在风险中性的假设条件下，我们利用Δ-对冲原理，推出分数跳-扩散过程下具有红利支付且有交易费用的回望期权价格所满足的偏微分方程.以下以欧式回望看跌期权为例进行讨论.

定理1在风险中性世界中，假定标的资产股票价格满足（1）式，到期日为T，则具有浮动执行价带有交易费的回望看跌期权在任意时刻t∈[0,T]的价格满足微分方程

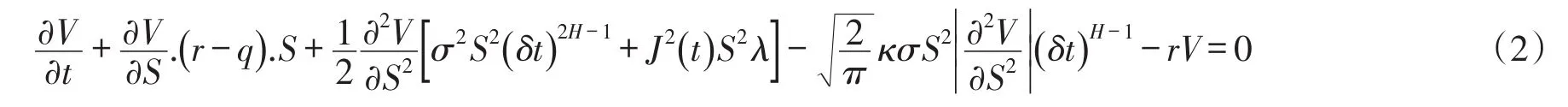
证明构造一投资组合，包括一份衍生证券V(S,t,J)和Δ份股票St，则在t时刻该资产组合的价值为Πt，可表示为

在时间段[t,t+δt]内，有

在离散时间段内，股票价格相应变化为

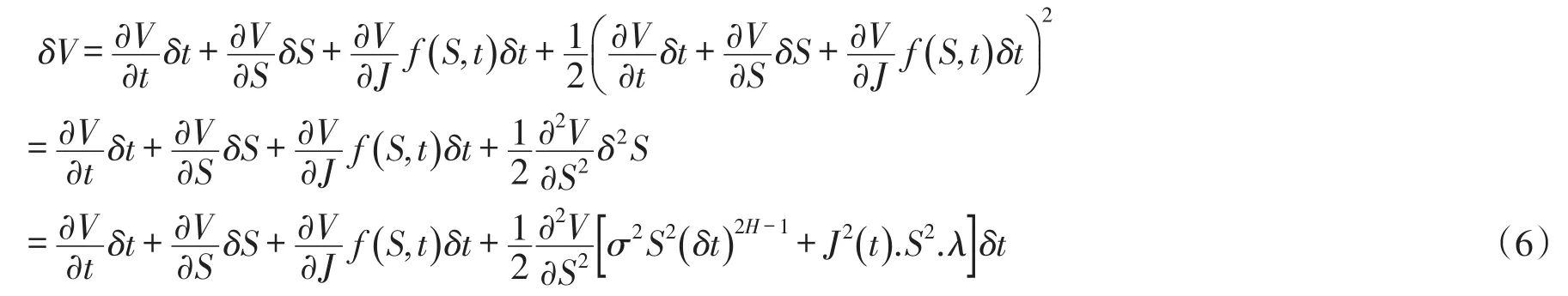
将（6）式代入（4）式，得

消去随机项，取

将（8）式代入（7）式，得到

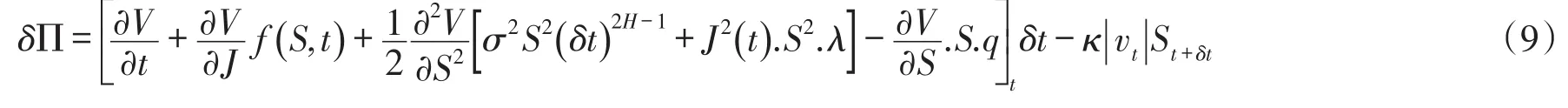
其中，

此外由方程（5）得

考虑交易费的条件数学期望值

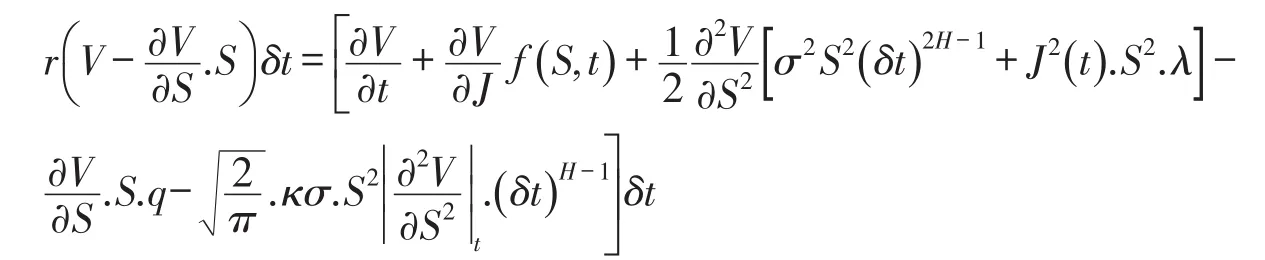
整理得

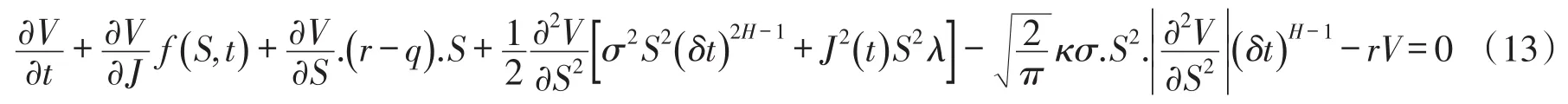
定义：

此边界条件的金融意义是指，当标的资产价格达到最大值时，回望看跌期权的价格对最大值的变化不再敏感.所以，当n→∞时，，即

将（16）式代入（13）式，最终我们得到了（2）式，定理证毕.

可以看出（2）式微分方程中并不包含路径因子J，路径变量仅是一个参量，只在边界条件和终值条件中出现.

2　模型求解

在给出分数跳-扩散模型下具有交易费用的回望看跌期权的定价公式之前，先引入以下引理.

引理1［7］标准布朗运动下的回望看跌期权定价模型为：

其解析解为

当r≠q时，

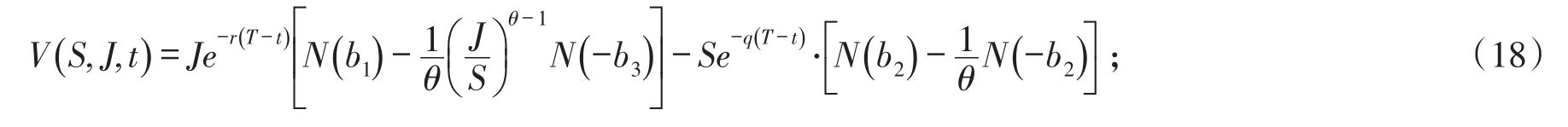
当r=q时，

定理2到期日为T，标的资产股票价格满足（1）式，则具有交易费用的回望看跌期权在任意时刻t的价值为：

当r≠q时，

当r=q时，

证明由定理1可得到分数跳-扩散过程下具有交易费用的回望看跌期权定价模型

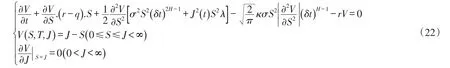
对于回望看跌期权的多头而言，到期日的收益为凸函数，因此保值因子，从而对于分数跳-扩散过程下具有交易费用的回望看跌期权，其定价模型与标准布朗运动下的回望看跌期权定价模型相比较，差别仅在于波动率，即：

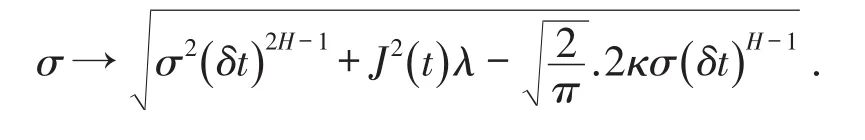
而对于回望看跌期权的空头而言，到期日的收益为凹函数，因此保值因子，从而相应于其定价模型，与标准布朗运动下做空的回望看跌期权定价模型相比较，差别也在于波动率，即：

下面以回望看跌期权的多头为例进行讨论.原方程（22）经过波动率修正，即

变换为方程：

由模型假设中的条件（iv）可知，在δt相当短的时间内，期权头寸只进行一次调整，因此δt是一个常数.而对于一个确定的期权而言，Hurst指数H与跳跃强度λ也都是常数，所以仅是依赖于σ的量，从而我们可通过引理1求出方程（24）的解析解.

3　结论

金融市场不仅存在长期记忆性以及突发性的“跳跃”情况，而且投资者还面临着不容忽视的交易成本，考虑带交易成本的期权定价问题更加贴近实际市场模型.本文通过引入分数跳-扩散过程，并结合带有交易费的情况，运用证券组合原理得到了回望期权的定价模型.其次利用波动率修正，将原有模型转化为标准布朗运动下的回望期权定价模型，从而得到了分数跳-扩散模型下具有交易费用的回望看跌期权定价公式.特别地，当我们得到的定价公式（20）和（21）即为标准布朗运动下带有交易费用和支付红利的回望看跌期权定价公式，而当时，得到的定价公式仅为标准布朗运动下的回望看跌期权定价公式.这表明了本文定价公式的普遍性，同时也说明了本文模型的正确性.

参考文献：

［1］DAI Min.A modified binomial tree method for currency lookback options［J］.Acta Mathematica Sinica，2000，16（3）：445-454.

［2］徐承龙，邬凯乐.带一般收益函数的欧式回望期权定价的Fourier方法［J］.同济大学学报，2005，33（7）：976-979.

［3］张艳秋，杜雪樵.随机利率下的回望期权的定价［J］.合肥工业大学学报，2007，30（4）：515-517.

［4］钱丽丽，柴俊.支付交易费的回望期权定价［J］.经济数学，2008，25（2）：143-147.

［5］孙玉东，薛红.分数跳-扩散过程下强路径依赖型期权定价模型［J］.西安工程大学学报,2010，24（1）：122-127.

［6］左玲，李时银，丁海燕.跳跃扩散型离散算术平均资产浮动执行价的回望买权定价［J］.厦门大学学报（自然科学版），2014，53（6）：774-779.

［7］姜礼尚.期权定价的数学模型和方法［M］.北京：高等教育出版社，2003：303-310.

Study of Pricing Lookback Options in the Fractional Jump-diffusion Model with Transaction Cost

WANG Weiwei，HAN Song
（Applied Mathematics Institute，Nanjing University of Finances and Economics，210046,Nanjing,Jiangsu,China）

Abstract：The Black-Scholes model has solved European option pricing in the efficient market successfully. This paper mainly studies the pricing of lookback options with transaction cost in the fractional jump-diffu⁃sion process under an inefficient market.Applying no-arbitrage principle and the securities combination tech⁃nology，we can establish options pricing model.And the pricing formulas for lookback options in the fractional jump-diffusion model with transaction cost are obtained through the model.The results in this paper extend and improve previously known results.

Key words：lookback option；fractional jump-diffusion model；transaction cost

作者简介：王伟伟（1990-），女，江苏盐城人，硕士生，研究方向：非线性分析与经济应用.

基金项目：国家自然科学基金资助项目（11071109）

收稿日期：2015-09-18

中图分类号：O 21

文献标识码：A

文章编号：2095-0691（2016）01-0004-05