钢管输送机构关键部件的强度校核及可靠性分析

郑 帅，柴晓艳，刘锡军，元 磊

(1．天津理工大学 天津市先进机电系统设计与智能控制重点实验室 天津 300384； 2.天津理工大学 机械工程学院，天津 300384)

钢管输送机构关键部件的强度校核及可靠性分析

郑 帅1,2，柴晓艳1,2，刘锡军1,2，元 磊1,2

(1．天津理工大学 天津市先进机电系统设计与智能控制重点实验室 天津 300384； 2.天津理工大学 机械工程学院，天津 300384)

运用ADAMS建立了钢管输送机构的动力学模型，通过仿真测量出机构关键部件的最大载荷，然后在ANSYS中求解出关键部件在最大载荷下的应力分布，从而根据第四强度理论进行关键部件的强度校核。根据ADAMS后处理模块中分析出载荷在正态分布下的均值和标准差，从而进一步对关键部件的可靠性进行分析，为关键部件的轻量化设计提供理论参考依据。

输送机构；关键部件；强度校核；可靠性

0 前言

近年来，钢管的产量迅速增加，在钢管的生产线中，钢管端面倒棱机是一种重要设备，钢管倒棱机由自动输送机构、铣头加工机构和夹紧装置三部分组成，自动输送机构周期性的将钢管送至夹紧装置，然后铣头加工机构对钢管两端进行平头、倒棱和去毛刺，从而提高了钢管的附加值，拓展了钢管的适应场合。本文研究的自动输送机构在运动过程中需要周期性的输送钢管，关键部件在运动中承受的载荷较大。因此有必要对机构的关键部件进行强度校核，本文利用ADAMS和ANSYS联合进行强度校核。在传统的零件设计中，认为零件的强度S和应力δ都是单值的，因此安全系数n=S/δ也是单值的，而这个安全系数是根据使用经验来确定的，它不能够说明所设计的零件在多大程度上是安全的，为此引入了可靠性设计。

在机械可靠性设计中，认为零件的应力和强度都是随机变量，载荷、零件的尺寸和其他设计参数也都是随机变量，它们服从一定的分布。在本文中，从可靠性的角度对关键部件进行分析，综合考虑关键部件的应力和强度在服从正态分布的情况下，用非线性概率来定量的说明关键部件到底有多可靠[1]，从而为后续的轻量化设计提供理论参考依据。

1 输送机构简介

输送机构简图如图1所示，杆1和杆3平行且长度相等，杆1、2、3在yoz面分为对称的两部分，如图2所示，在铰链点B和C处，各有一对滚子支撑工字钢，工字钢在两对滚子上作水平移动。该机构的运动过程分为四个行程，第一行程：活塞杆5驱动杆1、2、3和工字钢4上升，上升至工字钢4上的V型块接触钢管后，继续上升至杆1、3立直为止，则第一行程结束。第二行程：活塞杆8驱动杆7、6、工字钢4和钢管水平向右移动一个步进距离，即移动1 300 mm后机构停止运动，则第二行程结束[2]。第三行程是第一行程的逆运动过程，第四行程是第二行程的逆运动过程，机构通过升降运动和水平运动完成一个周期的输送运动，然后又开始下一周期的输送运动。

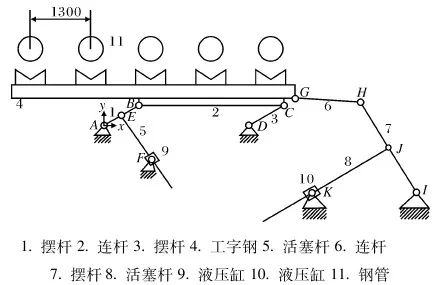
1.摆杆 2.连杆 3.摆杆 4.工字钢 5.活塞杆 6.连杆 7.摆杆8.活塞杆 9.液压缸 10.液压缸 11.钢管图1 钢管自动输送机构简图Fig.1 Pipe automatic conveying mechanism

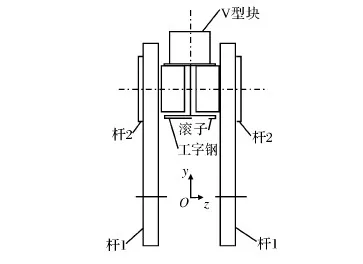
图2 输送机构摆杆1处左视图Fig.2 Left view of swinging rod 1 on conveying mechanism

2 传统的强度校核

本文首先在ADAMS中建立了输送机构的动力学模型，如图3所示，主要对机构中的关键部件摆杆1和摆杆7进行强度校核。通过前期的优化设计[3]，摆杆1在优化后铰链点E重合到铰链点B(见图1)，即在摆杆1上只有铰链孔A和B。在摆杆1的轴上还有并列的其他摆杆，考虑摆杆1处于最不利的情况下进行校核，即摆杆1处的液压缸没有顶起，摆杆1完全由轴驱动；对于摆杆7前期的优化设计后H、J、I孔都存在，没有发生摆杆1的重合现象，校核时要考虑两种受载情况，第一种最不利受载的情况，即液压缸没有顶起，完全由轴驱动；第二种正常受载情况。两种情况的驱动位置发生了变化。

为了进行在ANSYS中进行有限元分析，要求出各铰链点力的变化情况，对机构进行ADAMS动力学仿真后，在ADAMS后处理中即可获得载荷曲线[4]。图3、4和5为铰链点B、H和J在运动中的受力曲线。B点处的最大载荷为11302.3761，在x和y方向对应的分量分别为-7229.3627 N和8687.9239 N，H点处的最大载荷为3989.8496 N，在x和y方向对应的分量分别为3984.8844 N和198.9866 N，J点处的最大载荷为4346.2914 N，在x和y方向对应的分量分别为-1616.8035 N和-2438.7278 N，正负号只是代表力方向。

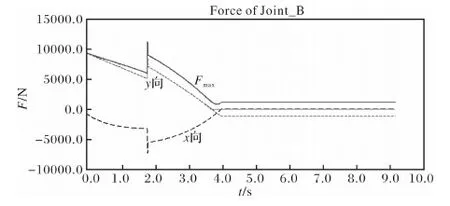
图3 铰链点B的受力曲线Fig.3 Stress curve of hinge point B

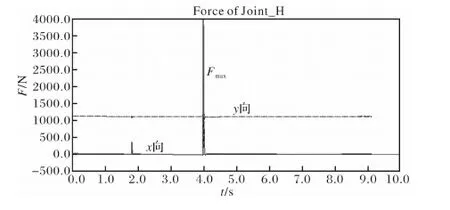
图4 铰链点H的受力曲线Fig.4 Stress curve of hinge point H

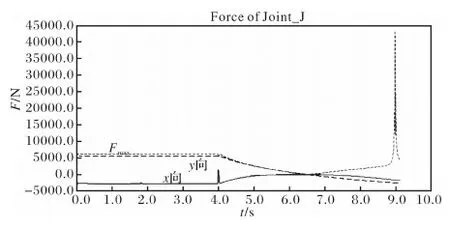
图5 铰链点J的受力曲线Fig.5 Stress curve of hinge point J

摆杆1和摆杆7通过solidworks按照实际尺寸进行三维建模，然后将摆杆1和摆杆7分别导入到ANSYS中，该机构所用材料为45号结构钢，在ANSYS中对零件定义材料属性、设置单元类型、划分网格，然后施加载荷，载荷值在ADAMS后处理中获取，求解结果如图6、图7和图8所示。

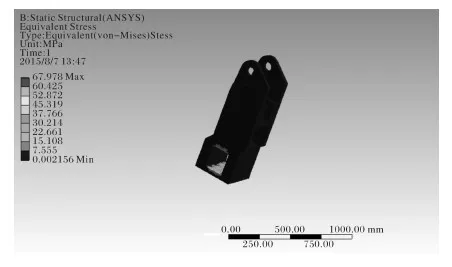
图6 摆杆1的应力分布Fig.6 Stress distribution of swinging rod 1

图7 摆杆7在第一种情况的应力分布Fig.7 Stress distribution of swinging rod 7 in the first case

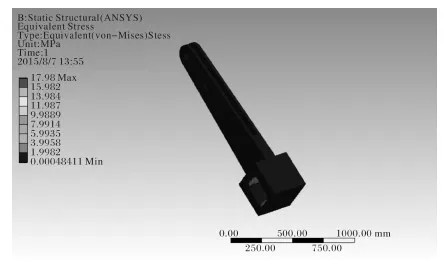
图8 摆杆7在第二种情况的应力分布Fig.8 Stress distribution of swinging rod 7 in the second case

根据第四强度理论对摆杆1和摆杆7进行强度校核，从图6中可以看出摆杆1的最大等效应力为67.978 MPa，该材料的屈服强度是350 MPa,故该零件是安全的，满足强度要求[5]。从图7中可以看出摆杆7第一种受载情况下的最大等效应力为59.69 MPa；从图8中可以看出，摆杆7第二种受载情况下的最大等效应力为17.98 Mpa，摆杆7在两种情况下最大等效应力都小于350 MPa,摆杆1和摆杆7的安全系数都较大，都是安全的。

3 可靠性分析

由于安全系数是根据使用经验来确定的，因此安全系数对于关键部件不能给出一个精确的度量，而在可靠性分析中，将应力和强度认为是服从某种分布的随机变量，可靠度能够定量地表示零件的安全可靠的程度，因此以概率论和数理统计为基础的可靠性分析方法比传统的安全系数法要更加合理[6]。图9为应力和强度的概率密度曲线，f(δ)为应力的概率密度曲线，f(S)为强度的概率密度曲线，μδ为应力的均值，μS为强度的均值。图9中阴影部分为强度和应力的干涉部分，表示零件的失效概率，即不可靠度，但是阴影部分的面积不能作为不可靠度的定量表示，因为在该干涉区内，强度大于应力的概率仍然是存在的。

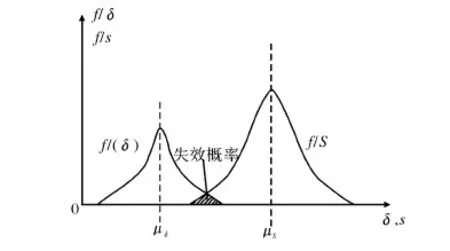
图9 应力和强度的概率密度曲线Fig.9 Probability density curve of stress and intensity

强度和应力在正态分布下的概率密度函数分别为

(1)

(2)

令y=S-δ,根据正态分布的加法定理，随机变量y也服从正态分布[7]，其均值和标准差分别为

μy=μS-μδ

(3)

(4)

随机变量y的概率密度函数为

(5)

可靠度为强度大于应力的概率，即

R=P[(S-δ)>0]=P(y>0)=

(6)

将式(6)标准化，令Z=(y-μy)/σy

(7)

则

dy=σydZ

(8)

Y=0时，Z的下限为

(9)

Y=+∞时，Z的上限也是+∞。

将式(7)、(8)代入式(6)中得

(10)

式中，R(t)表示可靠度；Z为服从标准正态分布的随机变量。

3.1 摆杆1的可靠性分析

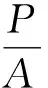
根据式(9)，Z的下限为

根据式(10)，摆杆1的可靠度为

根据标准正态分布的对称性，R(-22.0587)=F(22.0587)，其中F(t)表示不可靠度，通过查表得出F(10)>0.9999，而F(t)为关于t的增函数，故F(22.0587)>F(10)>0.9999,即R(-22.0587)>0.9999，说明摆杆1的可靠度在99.99%以上。

3.2 摆杆7的可靠性分析

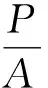
根据式(9)，Z的下限为

根据式(10)，摆杆7的可靠度为

根据标准正态分布的对称性，R(-22.2697)=F(22.2697)，其中F(t)表示不可靠度，通过查表得出F(10)>0.9999，而F(t)为关于t的增函数，故F(22.2697)>F(10)>0.9999,即R>0.9999，说明摆杆7的可靠度在99.99%以上。

通过对关键部件摆杆1和摆杆7进行可靠性分析，从概率论与数理统计的角度给出了关键部件的可靠程度，结果表明杆件很安全，为下一步进行关键部件的轻量化设计提供了参考依据。

4 结论

本文采用ADAMS和ANSYS联合求解的方法对自动输送机构的关键部件进行了传统上的强度校核和更加合理的可靠性分析，传统上的安全系数法将应力和强度看做单值，而可靠性分析将应力和强度看做随机变量。通过在ADAMS后处理程序PostPrecessor中求出最大载荷以及载荷的正态分布，然后在ANYS中求解应力分布，虽然摆杆1和摆杆7在传统的强度校核下是安全的，但是不能定量说明关键部件到底有多安全，而且根据安全系数法设计关键部件显得过于保守，会造成材料的浪费，因此对摆杆1和摆杆7进行了可靠性分析，结果表明二者的可靠度均在99.99%以上，是非常可靠的，这为后续的轻量化设计提供了重要的理论依据。

[1] 胡启国，刘元朋.机械可靠性设计及应用[M].电子工业出版社，2014:9-12.

[2] 柴晓艳，余小巧.φ406钢管端面铣头倒棱机自动送料机构的优化设计[J]. 重 型 机 械，2010(06)：41-46.

[3] 郑帅，柴晓艳，刘锡军，等.基于ADAMS的钢管端面倒棱机自动输送机构的优化设计[J].重型机械，2015(5).

[4] 陈德民，槐创锋，张克涛.精通ADAMS2005/2007虚拟样机技术[M].化学工业出版社，2010:188-191.

[5] 刘鸿文.材料力学[M].高等教育出版社，2010:243-248.

[6] 赵峰.基于响应面法的风力机叶片强度可靠性分析[D].华北电力大学，2009:26-27.

[7] 郝静如，米洁，李启光.机械可靠性工程[M].国防工业出版社，2008:48-49.

[8] 陈文华，贺青川，张旦闻. ADAMS2007机构设计与分析范例[M].机械工业出版社，2009:120-125.

[9] 邱宣怀.机械设计[M].高等教育出版社，2010:87.

Check of strength and reliability analysis of key parts for steel pipe conveying mechanism

ZHENG Shuai1,2，CHAI Xiao-yan1,2，LIU Xi-jun1,2，YUAN Lei1,2

(1.Tianjin Key Laboratory of the Design and Intelligent Control of the Advanced Mechatronical System,Tianjin University of Technology, Tianjin 300384, China；2. School of Mechanical Engineering, Tianjin University of Technology, Tianjin 300384,China)

Dynamic model of steel pipe conveying mechanism was established by ADAMS. The maximum loads of key components of the mechanism were measured by simulating, and then through ANSYS software the stress distribution of key parts are calculated under maximum load. According to the fourth strength theory, the strength check was completed for key parts. The mean and standard deviation on a load normal distribution were analyzed in ADAMS processing module. Then the key parts reliability were further analyzed to provide a theoretical reference for lightweight design.

conveying mechanism; key parts; strength check; reliability

2015-08-07；

2015-09-28

2014年天津市中小型创新基金项目(14ZXCXGX00334)

郑帅(1990-)，男，天津理工大学硕士研究生。

TH246

A

1001-196X(2016)03-0083-05