爆破对顺层岩质边坡稳定性的影响

王曙光，吁　燃

(贵州省交通规划勘察设计研究院股份有限公司， 贵阳　550001)



爆破对顺层岩质边坡稳定性的影响

王曙光，吁燃

(贵州省交通规划勘察设计研究院股份有限公司， 贵阳550001)

摘要：爆破作为边坡开挖的一种快速有效手段，广泛应用于土建施工中；而其爆炸冲击和爆轰气体对岩体节理面的锲入作用，对临近爆破区的边坡稳定性有负面影响。建立考虑爆破作用对边坡影响的计算模型，采用极限平衡法，从静力状态、爆破松动破坏、爆破振动3方面定量分析爆破作用对边坡的影响，并通过实际算例，对边坡稳定性进行分析计算，以验证爆破对边坡稳定性的影响。

关键词：稳定性分析；爆破作用；极限平衡法

顺层岩质边坡稳定性与岩体结构特征、产状，地下水位，岩体完整性及爆破振动等相关，其涉及到工程地质学、岩土工程学、爆炸力学以及地震工程学等学科的相关内容，其稳定性分析一直困扰着工程设计人员。边坡爆破开挖时，爆破振动会产生瞬时冲击作用，致使岩体产生质点振动加速度，质点振动加速度的传播会引起动荷载，造成局部岩体结构受损和岩石破碎脱落，削弱滑动面处的阻滑能力。同时，爆破振动惯性力的作用使得坡体整体下滑力增大，可能引起边坡动力失稳[1]。另外，爆破还会引起岩石应力重分布和地下水状态改变，形成一定范围的爆破松动区，从而进一步降低边坡的稳定性[2]。

顺层岩质边坡爆破开挖时，软弱夹层的存在对边坡稳定性有不利影响，主要表现在以下几方面：1) 软弱夹层的存在阻碍了爆破产生的应力波在岩体内部的传播，致使夹层带变成弱面，而应力波的拉伸易造成飞石危害[3]；2) 软弱夹层使得钻孔及装药较困难，易产生大块和根底，难以控制飞石；3) 由于岩体为低抗拉材料，故爆破振动产生的动荷载易引起软弱面松裂，使原有裂隙扩展延伸，造成岩体层裂，形成一定范围的爆破松动区，从而大大降低边坡的承载能力和稳定性[4]。文献[1]研究了高陡边坡爆破开挖技术和开挖爆破对特高陡边坡稳定性的影响，并提出了爆破振动灾害的有关控制技术。文献[4]通过含软弱夹层的顺层边坡深孔台阶爆破模型试验，推导了边坡潜在滑体的稳定系数与装药参数、岩体力学参数和边坡几何尺寸的定量关系，并通过实例研究，分析了爆破层裂效应对顺层岩质边坡动力稳定性的影响。文献[5]建立了爆破过程中软弱夹层的运动力学模型，应用爆轰流体动力学和气液两相流理论，导出了爆腔在爆轰气体作用下的运动速度、最终半径和扩腔时间与装药参数和软弱夹层力学参数的定量关系。文献[6]应用Mohr-Column准则，计算了在爆破振动作用下顺层岩质边坡的稳定安全系数，研究了安全系数随爆破拟静力系数变化的规律。目前，爆破动力作用下的边坡稳定性分析主要有拟静力法、有限滑移法和数值计算法。后2种方法由于难以确定边坡破坏时的变形、应力标准而很少单独使用，多采用拟静力法或拟静力法与数值计算相结合来分析动载荷作用下的边坡稳定性。本文考虑了爆破作用下岩体层间松动破坏和爆破振动影响，建立了爆破作用下顺层岩质边坡失稳模型，采用极限平衡法定量分析了爆破作用对顺层岩质边坡失稳的影响，并通过算例分析，验证了爆破对边坡稳定性的影响。

1边坡计算模型及稳定性分析

爆破作为岩质边坡的主要开挖手段，其对边坡的有害影响主要为爆炸应力波和爆破振动。顺层岩质边坡爆破开挖时，爆破振动会引起一定范围内的岩体层裂，导致层理面内摩擦角减小、内聚力降低，其振动惯性力使坡体下滑力增大。设计时，如何根据岩体内部条件和爆破施工外部参数正确确定层裂区的几何尺寸及层理面强度参数，是进行边坡稳定性分析、确定边坡设计方案的前提，也是边坡工程亟需解决的主要问题。本文下面将分析计算爆破振动对边坡稳定性的影响。为了便于计算，本文作如下假定：1) 由于本文研究对象为顺层边坡，假设滑动面为单一滑面，且视滑体为刚体；2) 滑动面破坏时其上的应力处于极限平衡状态，整个滑动面上边坡安全稳定系数相同；3) 不考虑地下水状态改变对于滑动面的粘聚力和内摩擦角的影响。

1.1不考虑爆破作用边坡稳定性分析

当不考虑爆破作用对边坡的影响时，假设岩层倾向垂直于路线走向，参照文献[7-8]的研究成果拟定路基边坡横断面，如图1所示。

图1中，H为坡高，α为边坡坡角，θ为岩层倾角，l为滑面长度，β为坡顶坡角，h为滑面上滑体高度，S为滑动分力，G为滑体重量，N为滑面上的支持力。按极限平衡法分析，边坡稳定性取决于由滑体重力产生的滑动分力S与滑面上的抗滑力R的比值大小。参考文献[7]，边坡稳定系数按下式计算：

图1　不考虑爆破影响的计算模型

(1)

式中：A为滑面面积，m2；V为滑体体积，m3； γ为岩体天然重度，kN/m3；c为滑面粘聚力，kPa；φ为滑面内摩擦角，(°)。

滑体体积和滑面面积为：

V=0.5 h·l·1·cosθ=0.5 hlcosθ

(2)

A=l·1=l

(3)

将式(2)、(3)代入式(1)，简化后得

(4)

由式(4)可知，如果不考虑爆破松动破坏影响，此时边坡稳定系数仅与滑体高度h、岩层倾角θ、粘聚力c、内摩擦角φ及岩体天然重度γ有关。

1.2考虑爆破作用边坡稳定性分析

1.2.1爆破松动破坏对顺层边坡稳定性的影响

爆破开挖边坡时，炸药爆炸后会产生剧烈的冲击波，而后冲击波衰减为应力波，而应力波的传播对于岩体的破碎具有非常重要的作用。由于岩体内部存在大量软弱结构面，如岩层层面、软弱夹层、节理裂隙等，因此，受爆破振动和爆破应力波传播的影响，边坡岩体结构面将出现松动。由于岩体结构面间咬合作用全部或部分丧失，导致其结构面抗剪强度降低。岩体结构面松动范围与岩体结构、岩石性质、爆破工艺及方法有关。深孔台阶爆破开挖边坡形成的松动带厚约10～15 m，而浅孔台阶爆破开挖和浅孔光面爆破开挖形成的松动带厚约1.5～2.5 m[7]。当考虑爆破松动破坏作用对边坡的影响时，对路基边坡横断面作了一些假定，如图2所示。

图2中，G1为未受爆破影响滑体重量，G2为受爆破影响层裂范围内滑体重量，S1为未受爆破影响下滑力，S2为受爆破影响层裂范围内下滑力，l1为爆破影响导致层间松动范围，l2为未受爆破影响长度。文献[7]提出，爆破后，岩层松动范围内的粘聚力降低了40%～60%，内摩擦角降低了10%～15%。

图2　考虑爆破松动破坏影响的计算模型

因此，当考虑爆破松动影响，抗滑力R1、R2由2部分组成，本文采用极限平衡法对边坡稳定性进行分析。此时，边坡稳定系数按下式计算：

(5)

式中：R1为未受爆破影响抗滑力，kN；R2为受爆破影响层裂范围内抗滑力，kN；c1为爆破层裂影响滑面的粘聚力，kPa；c2为未受爆破影响滑面的粘聚力，kPa；φ1为爆破层裂影响滑面的内摩擦角，(°)；φ2为未受爆破影响的内摩擦角，(°)。

受爆破层裂影响范围内的滑体重量为：

G1=0.5γl1h1cosθ·1=0.5γl1h1cosθ

(6)

未受爆破层裂影响范围内的滑体重量为：

G=0.5γlhcosθ·1=0.5γlhcosθ

(7)

G=G1+G2

(8)

l=l1+l2

(9)

将式(6)～(9)代入式(5)并化简，得

Ks=

(10)

比较式(4)和式(10)可知，如果不考虑爆破松动破坏影响，即c1=c2,l1=l2，此时式(10)即可简化成式(4)。但由于爆破应力波在结构面上产生透射和反射，当应力波到达层面反射时，使岩体受到拉伸作用，层面易松动破坏，此时安全系数受松动破坏长度和松动层面上的抗剪强度影响。

1.2.2爆破动力对顺层边坡稳定性的影响

顺层岩质路堑边坡爆破开挖过程中，爆破振动一方面使岩体的原有裂隙、层理等扩张、错动，致使岩体结构面的抗剪性能降低，摩擦阻力减小；另一方面，振动惯性力使得下滑力增加，对边坡稳定性产生不利影响。本文采用拟静力法来分析边坡稳定性。计算时，先将爆破振动荷载折算为等效静荷载，再对边坡进行静力分析。对路基边坡横断面作了假定，如图3所示。

图3　考虑爆破动力影响的计算模型

1.2.2.1水平振动加速度作用下的边坡安全系数

第i滑块所受的作用力如图4所示。图4中，Fi为爆破产生的水平动力，Ei与Ei+1为第i滑块左右相邻块作用于第i滑块的作用力，Gi为第i滑块滑体重量；Ni为第i滑块滑面上的支持力。

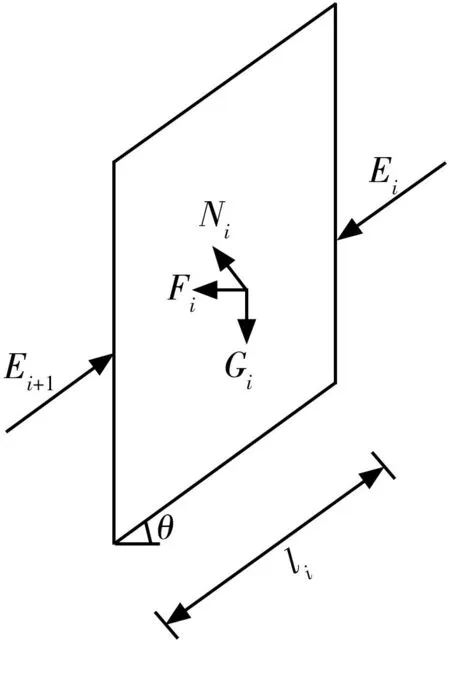
图4　受水平振动影响的第i滑块的作用力

由于第i滑块在垂直滑动面的法线方向无运动，故法向上受力平衡，即

Fisinθ+Ni=Gicosθ

(11)

则有

Ni=Gicosθ-Fisinθ

(12)

由于第i滑块的抗滑力为：

Ri=Nitanφi+cili=(Gicosθ-Fisinθ)tanφi+cili

(13)

第i滑块的下滑力为：

Si=Gisinθ+Ficosθ+Ei-Ei+1

(14)

故第i滑块的安全系数为：

(15)

则边坡安全系数为：

(16)

式(16)适合于复杂滑动面的边坡稳定性分析。由于本文研究对象为顺层边坡，前面假设边坡为单一滑面，不考虑地下水状态改变对于滑面粘聚力c和内摩擦角φ的影响，故可对式(16)进行简化，即

(17)

爆破动力的等效水平静力：

F=kma

(18)

式中：m为边坡滑体质量，kg；a为振动加速度，cm/s2；k为静力系数，一般为0.1～0.3。

振动加速度a与边坡有一定分布规律，根据实测值与距离的关系可得出线性回归方程，从而得出几何中心点处的加速度。

1.2.2.2竖直振动加速度作用下的边坡安全系数

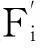
图5　受竖向振动影响的第i滑块的作用力

(19)

边坡安全系数为：

(20)

2算例分析

2.1工程概况

某1级公路横穿一斜坡，斜坡在自然条件下稳定性好。该公路路线走向为220°，岩层单斜产出，综合产状为316°∠31°，节理产状主要有265°∠85°、147°∠87°两组。强风化岩体节理很发育，岩体较破碎，胶结物为泥质，结合很差。下伏基岩为砂岩夹泥质粉砂岩，表层粉质粘土厚0～5 m，强风化层厚约5～7 m，岩层面结合很差。岩体类型为IV类，中风化岩体较破碎-较完整，结构面结合差，岩体类型为III类。工程地质横断面如图6所示。

赤平投影图如图7所示。图7中，节理J1为265°∠85°，节理J2为147°∠87°。分析图7可知，控制边坡稳定性的结构面为岩层层面(316°∠31°)，岩体易沿岩层面产生顺层滑塌失稳。

图7　赤平投影图

2.2计算采用的物理力学参数

根据工程地质调绘、钻探及取样试验，结合工程类比及文献[7]进行分析，确定各岩(土)层采用如下物理力学指标。

含碎石粉质粘土：γ=18 kN/m3，c=15 kPa，φ=10°，地基承载力基本容许值[fa0]=160 kPa。

强风化砂岩夹泥质粉砂岩：γ=21 kN/m3，[fa0]=500 kPa。

中风化砂岩夹泥质粉砂岩：γ=25 kN/m3，[fa0]=1 000 kPa。

强风化岩体层间软弱结构面：c=30 kPa，φ=15°。

中风化岩体层间软弱结构面：c=40 kPa，φ=21°。

2.3稳定性分析计算

边坡坡率采用1∶1～1∶1.25，计算不考虑爆破作用、考虑爆破松动破坏、考虑爆破振动作用3种情况对边坡的影响，并得到如下结果。

1) 不考虑爆破作用对边坡稳定性的影响时，岩层面的抗剪强度指标为：c=30 kPa、φ=15°，θ=29°，A=271.3 m2，l=65.8 m。代入式(1)计算得Ks=1.2。因此，当不考虑爆破作用对边坡层面影响时，边坡按1∶1～1∶1.25放坡开挖，边坡处于稳定状态。

2) 考虑爆破松动作用对边坡的影响时，由文献[7]的研究成果可知，层间抗剪强度受爆破作用影响，爆破松动后，考虑岩层层面上的粘聚力降低50%，内摩擦角降低10%。此时岩层面的抗剪强度指标变为：c2=15 kPa，φ2=13.5°，c1=30 kPa，φ1=15°，A1=158.5 m2，A2=112.8 m2，l1=36.3 m，l2=29.5 m。将上述参数代入式(5)计算，得Ks=1.02，表明边坡处于临界状态。

3) 考虑爆破振动作用对边坡的影响时，本文对水平爆破动力作用进行了稳定性分析。此时岩层面的抗剪强度指标变为：c=30 kPa，φ=15°，A=271.3 m2，l=65.8 m。爆破动力等效水平静力按式(18)计算，其中静力系数k取0.15，并根据爆破加速度实测值线性回归出振动加速度a沿边坡的分布规律，且估算出几何中心点的加速度为3.1g。将上述参数代入式(17)计算，得Ks=0.58，表明边坡处于不稳定状态。

由算例分析可知，当不考虑爆破作用对于边坡稳定性的影响时，边坡处于稳定状态；当考虑爆破松动破坏对于边坡稳定性影响时，边坡处于临界状态；当考虑爆破振动作用对边坡稳定性影响时，边坡处于不稳定状态。因此，对边坡稳定性进行计算时，必须考虑爆破作用对于边坡稳定性的影响，选择合适的爆破方法，且不合适的爆破方法可能导致边坡出现牵引式滑坡。由于岩体结构特征是影响边坡稳定的主要内部因素，而爆破开挖是诱发边坡稳定失稳的外在因素，因此，选择合适的爆破方法，控制爆炸应力波的破坏范围，尽量消除爆破振动的影响，是保证边坡稳定的关键[9]。

3结论与建议

本文建立了顺层边坡失稳模型，推导了考虑爆破振动对边坡稳定性影响的安全系数，得到以下结论及建议。

1) 爆破开挖是引发边坡产生滑坡的重大诱因，对边坡进行稳定性分析时，需考虑其对边坡稳定性的影响。不同的爆破方法和工艺将产生不同的后果，因此，对于高陡的硬质岩边坡，建议采用光面预裂爆破技术。

2) 爆破振动对顺层边坡稳定性的影响主要为松动破坏和爆破动力影响。爆破动力对含有软弱夹层的顺层边坡尤为显著，在边坡设计和边坡稳定性分析时不能忽视。

3) 由于拟静力法未包括爆破地震波的频谱结构差异、相位差等，因此，采用拟静力法计算边坡安全稳定系数时，仅考虑了某一条块的峰值加速度，加之测试仪器误差及环境因素影响，安全稳定系数结果很难反映爆破振动的实际情况。此外，由于计算时并未考虑岩体结构特征、几何尺寸和外来作用的随机性，因此采用单一的安全系数来评价边坡稳定性和可靠性不易达成共识，建议采用可靠性理论来评价工程结构的稳定性和可靠度[9]。

参 考 文 献

[1]刘美山.特高边坡开挖爆破技术及其对边坡稳定性的影响[D].合肥：中国科学技术大学，2005.

[2]杨聃.爆破震动对岩质高边坡的影响及控制措施研究[J].人民黄河，2006，28(10)：68-69.

[3]葛克水，陈庆寿.地质条件在爆破工程实践中的重要影响[J].西部探矿工程，2001(1)：90-91.

[4]宋小林.层状岩体爆破的层裂效应及其对顺层边坡稳定性的影响研究[D].成都：西南交通大学，2007.

[5]宋小林，张继春，郭学彬，等.钻孔爆破过程中顺层边坡软弱夹层的运动力学模型[J].应用力学学报，2010，27(3): 559-564.

[6]李维光，张继春.爆破振动作用下顺层岩质边坡稳定性研究[J].爆破与冲击，2007，5(27): 426-430.

[7]李安洪，周德培，冯君，等.顺层岩质边坡稳定性分析与支挡防护设计[M].北京：人民交通出版社，2011.

[8]交通部第二公路勘察设计院.路基[M].北京：人民交通出版社，1996.

[9]李维光.爆破振动作用下顺层岩质边坡稳定性研究[D].成都：西南交通大学，2008.

Influences of Blasting on Stability of Bedding Rock Slopes

WANG Shuguang, XU Ran

Abstract:As a rapid and effective way for excavation of side slopes, blasting is extensively applied in civil construction; while the mounting effect of its explosive impact and detonation gases to joint surface of rocks raises negative influences on stability of side slopes adjacent to blasting area. This paper establishes a computing model in consideration of influences of blasting effect on side slopes, and quantitatively analyzes influences of blasting effect on side slopes from 3 aspects including static states, blasting loosening damage and blasting vibration by means of the limit equilibrium method; and analyzes and calculates stability of side slopes via actual calculation examples to verify influences of blasting on stability of side slopes.

Keywords:stability analysis; blasting effect, limit equilibrium method

文章编号：1009-6477(2016)01-0017-05

中图分类号：U416.1+4

文献标识码：A

作者简介：王曙光(1983-)，男，湖南省娄底市人，硕士，工程师。

收稿日期：2015-10-21

基金项目：国家自然科学基金项目(51208522)；贵州省交通运输厅科技项目(2012122033)

DOI:10.13607/j.cnki.gljt.2016.01.005