横风作用下货物列车通过大跨度铁路斜拉桥的走行安全性研究

郭向荣,何　玮,朱志辉,何旭辉

(1.中南大学 土木工程学院，湖南 长沙　410075；2.中南大学 高速铁路建造技术国家工程实验室，湖南 长沙　410075)

铁路货运因其显著的经济效益而受到各国铁路部门的广泛重视，其桥上线路的运营安全一直备受学者们的关注。龙卫国等采用数值计算方法研究了重载列车通过简支梁桥时桥梁的垂向动力响应[1]；魏玉光等在考虑桥梁适应性的前提下研究了敞车最大合理轴重[2]；李奇等研究了轻重混编货物列车通过中小跨度桥梁时的车桥动力响应[3]。以往由于铁路桥梁跨度不大，且大多是刚度很大的简支梁桥，对风荷载不敏感，因此学者们在研究货物列车的车桥动力响应时大多未考虑风荷载因素的影响[4]。随着我国铁路运输的发展，铁路桥梁的跨度不断增加，大跨度铁路桥梁的车桥动力响应对风荷载愈加敏感，因此，在研究货物列车通过大跨度桥梁的走行安全性时，应综合考虑风荷载的影响。

本文以铁路专用洞庭湖特大桥和C80型敞车编组货物列车为研究对象，采用桥梁与列车三分力系数的风洞试验结果，将脉动风荷载作为外部激励、轨道不平顺作为系统的自激激励源，建立考虑风荷载作用的车桥系统耦合振动方程进行横风作用满载和空载2种工况下货物列车通过大跨度铁路斜拉桥时的走行安全性分析。

1　风—车—桥系统动力学模型的建立

1.1　列车计算模型

货物列车车辆的计算模型由车体、构架及轮对共7个刚体以及摇枕悬挂装置(又称第二系悬挂)组成。本文进行耦合振动分析时采用以下假定：①车体、构架和轮对均为刚体； ②不考虑轮对侧滚和点头的自由度；③不考虑列车纵向自由度；④弹簧、蠕滑力为线性关系，阻尼为黏滞阻尼；⑤轮对与桥上轨道竖向位移保持一致。由此确定车体及前后构架在空间上有侧摆、侧滚、点头、摇头以及浮沉等5个自由度，每个轮对有侧摆和摇头2个自由度，因此4轴机车车辆共有23个自由度[5]。

本文建立C80型敞车编组货物列车的计算模型，车体各部分尺寸如图1所示。C80型敞车主要技术参数为车辆长度12 m，车辆定距8.2 m，有效容积87 m3，轴重25 t，车轮直径0.84 m，正常运营速度100 km·h-1。

1-车钩缓冲装置；2-转向架；3-底架；4-侧墙；5-空气制动装置；6-下侧门；7-牵引杆缓冲装置；8-端墙；9-手制动装置；10-撑杆装置

1.2　桥梁计算模型

铁路桥主梁多采用桁架结构，本文建立的桥梁计算模型基于洞庭湖特大桥，该桥是新建荆岳铁路线上的1座大跨度三塔双索面钢箱钢桁叠合梁斜拉桥，西起君山岸、东至岳阳岸。作为1座铁路专用大跨度斜拉桥，该桥的主跨与边跨布置为98 m+140 m+406 m+406 m+140 m+98 m，桥梁全长1 290 m，桥面为正交异性整体钢桥面，主梁横断面形式为整体钢箱与钢桁叠合，如图2所示。其中，桁架结构为不带竖杆的华伦式桁架，钢箱结构外侧设有风嘴以提高结构的抗风性能。

图2　主梁断面图(单位：mm)

本文桥梁计算模型采用空间梁-板-索系有限元分析模型。桥塔、桥墩结构及桁架结构采用空间梁单元；箱梁结构采用空间板单元；斜拉索采用空间索单元。空间梁单元采用二节点空间直梁单元，考虑其竖向、横向受弯以及扭转变形，每个节点考虑3个线位移与3个转角位移，整个单元有12个自由度；空间板单元的节点数为4，每个节点考虑沿轴向的2个线位移，整个单元有8个自由度；空间索单元的节点数为2，节点自由度数为3。墩底处地基基础的刚度分别叠加于相应的节点上。由此建立的斜拉桥有限元模型如图3所示。

图3　桥梁有限元模型

1.3　脉动风场

在风—车—桥耦合系统中，可将脉动风场近似看做沿桥梁顺桥向若干点处随机风波的合成[6-8]，脉动风场可表示为一维多变量的平稳高斯随机过程，对于1个零均值的一维n变量高斯过程fj(t)，j=1, 2, …，n，其互谱密度矩阵S0(ω)可以分解为

S0(ω)=H(ω)HT(ω)

(1)

式中：H(ω)为S0(ω)矩阵Cholesky分解后的下三角矩阵；HT(ω)为H(ω)矩阵的共轭转置矩阵，各矩阵具体形式详见文献[9]。

参照Shinozuka的相关理论，随机过程的样本可以由下式模拟。

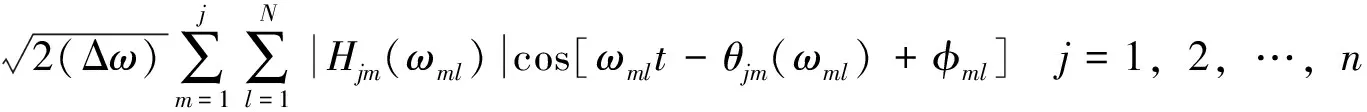
(2)

Gjm(ωml)=

式中：N为足够大的正整数；Δω为计算频率的增量；Φml为分布在[0,2π]之间的随机变量；ωml为双索引频率；Hjm(ωml)为H(ω)的元素；θjm(ωml)为Hjm(ωml)的复角；Sjm(ωml)为矩阵S0(ω)的元素；λ为无量纲的衰减因子，取值范围约为7～10；v(z)为桥面高度z处的平均风速；d为距离增量。

本文在模拟脉动风场时，考虑了桥址各点之间的空间相关性，采用20，22.5和25 m·s-1这3种风速，以桥址处君山岸桥头为起点，沿桥上线路共模拟了27个风速点，风速点的水平间距为50 m，2个风速模拟点之间的脉动风速时程曲线利用其相邻的2个模拟点进行线性内插求得。风速时程的计算时间步长取0.1 s，样本长度为180 s。图4给出了平均风速为20 m·s-1时第18个风速点(岳阳岸桥尾侧主跨跨中附近)处的脉动风速时程曲线。

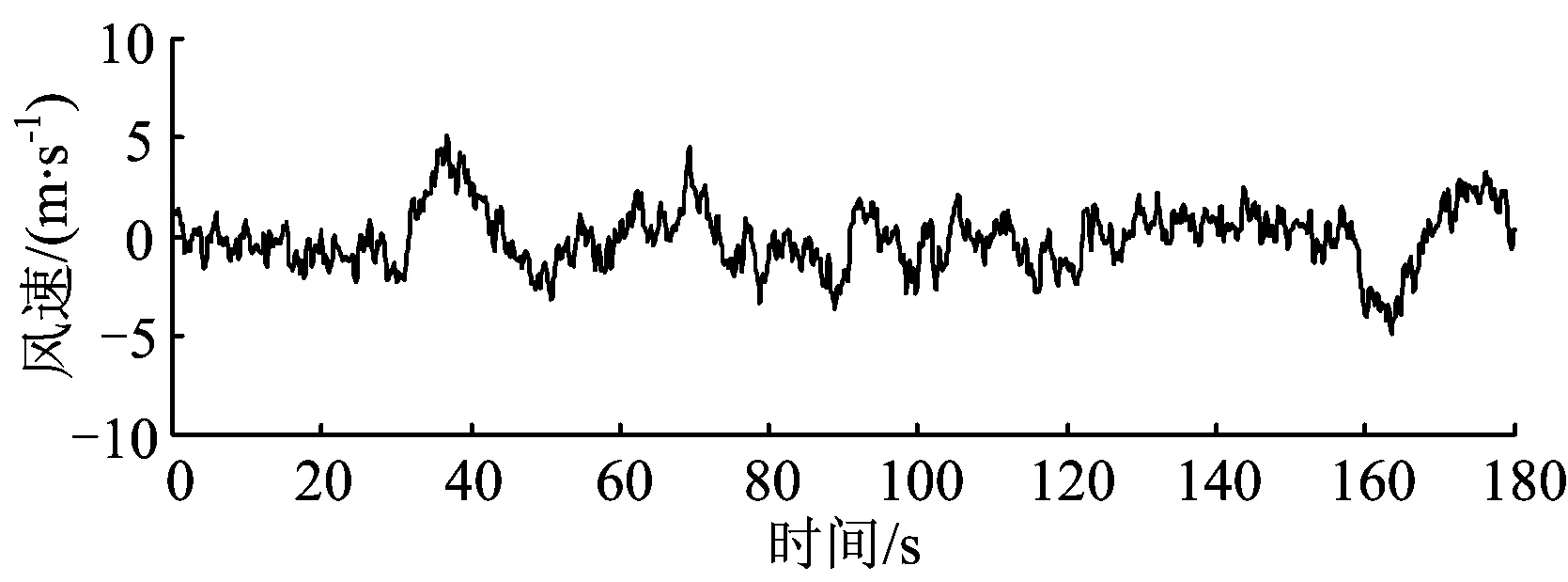
图4　沿主梁方向第18个风速点处的脉动风速时程曲线

1.4　风—车—桥系统动力学方程

根据弹性系统动力学总势能不变原理及形成矩阵的“对号入座”法则，本文将桥梁与桥上列车视为1个整体系统，其中，轨道不平顺作为系统的自激激励源，风荷载作为外部激励，建立的风—车—桥耦合系统非线性振动方程为

(3)

式中：Mb和Mt分别为桥梁和列车的质量矩阵；Cb，Ct，Kb和Kt分别为桥梁和列车的阻尼矩阵和刚度矩阵；Cbtb，Ctb，Kbtb和Ktb分别为车桥耦合系统中由桥梁振动速度引起的阻尼矩阵和刚度矩阵；Cbt，Ctt，Kbt和Ktt分别为车桥耦合系统中由列车振动速度引起的阻尼矩阵和刚度矩阵；Cbw和Kbw分别为由桥梁自身的自激风力所产生的阻尼矩阵和刚度矩阵；Fbe为作用在桥梁结构上的列车自重荷载向量；Fbw和Ftw分别为作用在桥梁和列车上的风荷载向量。

式(3)中各质量矩阵、阻尼矩阵和刚度矩阵的具体形式详见文献[5]和文献[10]，桥梁及桥上列车风荷载采用式(4)—式(6)计算。

阻力：FH=0.5ρv2HLCH

(4)

升力：FV=0.5ρv2BLCV

(5)

扭矩：M=0.5ρv2B2LCM

(6)

式中：ρ为空气密度，取1.225 kg·m-3；L为桥梁(或列车)的长度；H和B分别为桥梁(或列车)断面的高度和宽度；CH，CV和CM分别为体轴坐标系下桥梁(或列车)的阻力系数、升力系数和扭矩系数。

由于不同工况下列车与桥梁的气动力系数存在差异，因此各工况下列车与桥梁受到的风荷载也不同。在进行风—车—桥耦合计算时，平均风速作为定量提前施加在结构上，脉动风速作为对时间的变量参与时程计算。

2　计算工况

以往研究结果表明，货物列车在满载和空载2种工况下的气动性能有较为明显的差异[11]，因此本文考虑了货物列车分别在满载和空载2种工况下单线横向迎风及背风行车共4种工况。为了分别获取满载和空载工况下车—桥系统的三分力系数，风洞试验时在车体模型顶部加装盖板模拟满载工况，空载工况时则无盖板。表1为车桥耦合状态下风攻角为0°、满载和空载货物列车分别位于桥梁迎风侧和背风侧时列车和桥梁三分力系数的风洞试验结果。

表1　各工况三分力系数风洞试验结果

3　结果分析

本文采用朔黄线神池—肃宁段上行线路实测轨道不平顺谱作为系统自激激励，列车编组为2机车+25敞车。在进行数值计算时，采用Wilson-θ逐步积分法直接求解风—车—桥耦合系统振动方程。

3.1　满载工况

在横风作用下，车速为100 km·h-1的满载货物列车通过大跨度铁路斜拉桥时，桥梁和列车的动力响应最大值见表2和表3。从表2可以看出：随风速的增大，满载工况下桥梁跨中处桥面横向动力响应有增大趋势，而竖向动力响应变化不明显，其原因在于横桥向是风的来流方向，风速对桥梁横向动力响应的影响远大于竖向动力响应。从表3可以看出，满载货物列车以100 km·h-1通过大跨度铁路专用斜拉桥时，风速从20 m·s-1增大至25 m·s-1，列车脱轨系数和横向摇摆力增大较为明显，但脱轨系数与轮重减载率均未超标，背风工况的车桥系统动力响应大于迎风工况，其原因在于当列车行驶至桥梁跨中处时，跨中处桥面不仅受风荷载的作用，还受相对于桥面中轴线偏心列车荷载的作用，迎风工况下该偏心荷载使桥面产生与横向风反向的横向位移，而背风工况下该偏心荷载使桥面产生与横向风同向的横向位移。

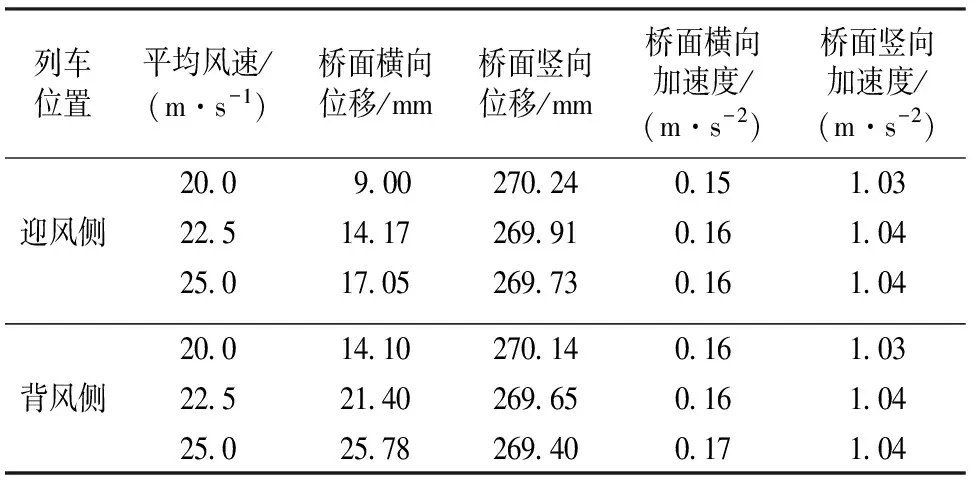
表2　满载工况桥梁响应最大值

表3　满载工况车辆响应最大值

满载迎风工况下，车速为100 km·h-1时，岳阳方向主跨跨中桥面横向位移时程曲线如图5所示，头车第1轮对相对于轨面位移时程曲线如图6所示。从图5可以看出，在时间为30 s时，岳阳方向主跨跨中桥面横向位移的波动明显增大，这是由于列车此时刚好到达岳阳方向主跨跨中处。从图6可以看出，在时间分别为16和30 s时，头车第1轮对相对于轨面位移的波动均明显增大，这是由于列车在16和30 s时刚好分别到达桥梁东西两侧主跨的跨中处。综合来看，桥面风速对满载货物列车经过桥梁跨中处时的车桥动力响应影响较大。

图5　满载迎风工况下岳阳方向主跨跨中桥面横向位移时程曲线

3.2　空载工况

在横风作用下，空载货物列车通过大跨度铁路斜拉桥时，不同车速和风速下桥梁与列车的动力响应最大值见表4和表5。从表4可以看出，随风速的增大，空载工况下桥梁跨中桥面横向动力响应有增大趋势，而竖向动力响应变化不明显，这与满载工况的计算结果一致。从表5可以看出，在车速为40 km·h-1、桥面风速为20 m·s-1时，列车脱轨系数和轮重减载率均能够满足安全行车的要求；在车速为40 km·h-1、桥面风速为25 m·s-1时，列车脱轨系数和轮重减载率均超标；在车速为60 km·h-1、桥面风速为20 m·s-1时，列车轮重减载率大于0.6，属于超标。从计算结果上看，风速和车速对空载货物列车通过大跨度铁路斜拉桥的行车安全影响均较大；迎风工况与背风工况的车桥系统动力响应差别不大，原因在于空载时列车质量较小，此时相对于桥面中轴线的偏心列车荷载与风荷载的叠加效应不明显。

表5　空载工况下列车响应最大值

空载迎风工况下，当车速为40 km·h-1时，岳阳方向主跨跨中桥面横向位移时程曲线如图7所示，头车第1轮对相对于轨面位移时程曲线如图8所示。从图7可以看出，在时间为76 s时，岳阳方向主跨跨中桥面横向位移的波动明显增大，这是由于此时列车刚好到达岳阳方向主跨跨中处。从图8可以看出，在时间分别为40和76 s时，头车第1轮对相对于轨面位移的波动均明显增大，这是由于列车在40和76 s时刚好分别到达桥梁东西两侧主跨的跨中处。由此可知，空载和满载工况下桥面风速对货物列车经过桥梁跨中处时车桥动力响应的影响均较大。

图7　空载迎风工况下岳阳方向主跨跨中桥面横向位移时程曲线

图8　空载迎风工况下头车第1轮对相对于轨面位移时程曲线

比较满载和空载工况下风—车—桥系统动力响应计算结果可知，空载货物列车通过大跨度铁路斜拉桥时列车响应明显大于满载时，这是由于空载货物列车的质量较小，而车体所受横向气动力较大。因此，当桥面风速相同时，横风作用下空载货物列车通过大跨度铁路斜拉桥时的行车安全问题更应受到重视。

4　结　论

(1)在桥面风速为25 m·s-1情况下，车速低于100 km·h-1时满载货物列车的脱轨系数与轮重减载率均未超标；当桥面风速由20 m·s-1增大至25 m·s-1时，满载货物的列车脱轨系数与轮重减载率变化不明显。

(2)在桥面风速为25 m·s-1情况下，车速高于40 km·h-1时空载货物列车的脱轨系数与轮重减载率均超标；相对于满载工况，空载工况下桥梁和列车动力响应受车速和桥面风速的影响均较大，而受列车处于桥面迎风及背风侧位置的影响较小。

(3)在横风作用下，空载货物列车通过大跨度铁路斜拉桥时的列车响应明显大于满载时，这是由于空载货物列车的自重较小，而车体所受横向气动力较大。因此本文建议空载货物列车通过大跨度铁路斜拉桥时应根据桥面风速合理降低车速。

[1]龙卫国, 蒋丽忠, 陈令坤. 重载列车过桥时桥梁的垂向动力分析[J]. 振动与冲击, 2013, 32(12): 140-149.

(LONG Weiguo, JIANG Lizhong, CHEN Lingkun. Vertical Dynamic Analysis of a Bridge during a Heavy Haul Train Passing Through[J]. Journal of Vibration and Shock, 2013, 32(12): 140-149. in Chinese)

[2]魏玉光, 韦俊峰, 于跃斌. 运煤专用敞车最大合理轴重研究[J]. 中国铁道科学, 2014, 35(3):97-101.

(WEI Yuguang, WEI Junfeng, YU Yuebin. Research on the Maximum Reasonable Axle Load of New Coal Open-Top Wagon[J]. China Railway Science, 2014, 35(3):97-101. in Chinese)

[3]李奇, 吴定俊, 李俊. 混编货车通过中小跨度桥梁时车桥振动分析[J]. 同济大学学报：自然科学版, 2007, 35(2): 171-175.

(LI Qi, WU Dingjun, LI Jun. Train-Bridge Vibration Analysis of Mix-Marshalling Freight Trains’ Traversing Medium and Small Span Bridges[J]. Journal of Tongji University：Natural Science, 2007, 35(2): 171-175. in Chinese)

[4]LIU K, REYNDERS E, DE-ROEEK G, et al. Experimental and Numerical Analysis of a Composite Bridge for High-Speed Trains[J]. Journal of Sound and Vibration， 2009, 320(1/2): 200-220.

[5]曾庆元, 郭向荣. 列车桥梁时变系统振动分析理论与应用[M]. 北京:中国铁道出版社, 1999.

[6]SCANLAN R H. The Action of Flexible Bridge under Wind II: Buffeting Theory[J]. Sound and Vibration, 1987, 60(2): 201-211.

[7]LI Y L, LIAO H L, QIANG S Z. Simplifying the Simulation of Stochastic Wind Velocity Fields for Long Cable-Stayed Bridges[J]. Computers and Structures, 2004，82(20): 1591-1598.

[8]李永乐, 强士中, 廖海黎. 风—车—桥系统非线性空间耦合振动研究[J]. 土木工程学报, 2005, 38(7): 61-70.

(LI Yongle, QIANG Shizhong, LIAO Haili. 3-D Coupled Vibration of Wind-Vehicle-Bridge System[J]. China Civil Engineering Journal, 2005, 38(7): 61-70. in Chinese)

[9]DEODATIS G. Simulation of Ergodic Multivariate Stochastic Processes[J]. Journal of Engineering Mechanics, 1996,122(8): 778-787.

[10]XU Youlin, ZHANG Nan, XIA He. Vibration of Coupled Train and Cable-Stayed Bridge System in Cross Winds[J]. Engineering Structures, 2004, 26(10): 1389-1406.

[11]何华, 田红旗, 熊小慧，等. 横风作用下敞车的气动性能研究[J]. 中国铁道科学, 2006, 27(3): 73-77.

(HE Hua, TIAN Hongqi, XIONG Xiaohui, et al. Study on the Aerodynamics Performance of Gondola Car under Cross Wind[J]. China Railway Science, 2006, 27(3): 73-77. in Chinese)

[12]XIA He, GUO Weiwei, ZHANG Nan, et al. Dynamic Analysis of a Train-Bridge System under Wind Action[J]. Computers and Structures, 2008，86(19): 1845-1855.

[13]HE X H, ZOU Y F, WANG H F, et al. Aerodynamic Characteristics of a Trailing Rail Vehicles on Viaduct Based on Still Wind Tunnel Experiments[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014，135(1): 22-33.

[14]张楠, 夏禾, 郭薇薇，等. 京沪高速铁路南京大胜关长江大桥风—车—桥耦合振动分析[J]. 中国铁道科学, 2009, 30(1): 41-47.

(ZHANG Nan, XIA He, GUO Weiwei, et al. Analysis on the Wind-Vehicle-Bridge Coupling Vibration for Nanjing Dashengguan Yangtze River Bridge of Beijing-Shanghai High-Speed Railway [J]. China Railway Science, 2009, 30(1): 41-47. in Chinese)