基于信息扩散理论的雷电灾害事故预测

吴安坤 曾 勇 张淑霞贵州省防雷减灾中心



基于信息扩散理论的雷电灾害事故预测

吴安坤 曾 勇 张淑霞
贵州省防雷减灾中心

【摘 要】基于信息扩散理论对雷电灾害事故频数进行预测，以贵州近12年历史雷灾样本为例，分别从特别重大、重大、较大、一般雷灾事故四个等级作风险预测，以弥补雷灾样本少、其概率分布难以确定等缺陷，为防雷减灾提供决策性建议。同时，对于此类自然灾害的风险预测有一定的借鉴作用。

【关键词】信息扩散模型；雷灾事故等级；灾害重现率

雷电灾害泛指雷击或雷电电磁脉冲入侵和影响造成人员伤亡或物体受损，其部分或全部功能丧失，酿成不良的社会和经济后果的事件。作为自然界中影响人类活动的最重要灾害之一，无时不刻的影响着人身安全、经济建设、信息、航天、军事、交通、生态及体育活动安全，已经被联合国列为“最严重的十种自然灾害之一”[1]。因此，对雷电灾害事故的预测研究分析显得尤为重要。但以往对雷电灾害的分析采取概率统计的方法较多，通常需要样本容量尽可能大，一般至少达到30个以上，样本容量小于30的情况下会导致分析结果波动性较大，存在大幅度偏离实际的情况。由于受地域、经济、社会关注度等因素的影响，雷电灾害统计资料存在样本小、容量低等特点。为解决此类问题，黄崇福教授提出基于信息扩散理论的灾害风险评估方法[2]，以解决小样本事件的缺陷。信息扩散模型是以历史灾情资料为依据, 将样本数据进行集值化的一类模糊数学方法。因该模型对概率分布未知、样本数量较少的自然灾害具有良好的适用性，从而成为模糊不确定性方法中运用最为广泛的模型之一。被广泛用于洪涝灾害[3-5]、气象灾害[6-8]、火灾[9]和地震[10]等特定灾害评估与预测中。为此，本文将信息扩散模型应用于雷电灾害事故的评估预测，以贵州历史雷灾资料为背景，预测不同强度等级雷灾事故发生的可能性，以期为全省防雷减灾提供决策建议。

1 资料处理及研究方法

1.1 资料处理

根据规范[11]划分标准：特别重大雷电灾害事故指因雷击造成4人以上身亡，或3人身亡并有5人以上受伤，或没有人员身亡但有10人以上受伤，或直接经济损失500万元以上的雷电灾害事故；重大雷电灾害事故指因雷击造成2-3人身亡，或1人身亡并有4人以上受伤，或没有人员身亡但有5-9人受伤，或直接经济损失100万元至500万元以下的雷电灾害事故；较大雷电灾害事故指因雷击造成1人身亡，或没有人员身亡但有2-4人受伤，或直接经济损失20万元以上100万元以下的雷电灾害事故；一般雷电灾害事故指因雷击造成1人受伤或直接经济损失20万元以下的雷电灾害事故。统计贵州近12年不同等级雷灾事故，作为进一步处理的分析样本。

1.2 信息扩散技术

在应用信息扩散模型中，扩散函数与扩散系数直接关系到结果准确与否的关键。本文选用的是最简单的正态扩散函数。黄崇福教授对不同扩散函数进行了验证。结果表明，在样本容量不大的情况下，简单正态分布要优于指数分布和对数正态分布。对于扩散系数，许多研究者也对此做了探讨与改进。

设xi为历史雷灾发生的样本，全省m年内实际记录为x1、x2、x3、...、 xm

则，Xi={x1、x2、x3、...、 xm}，X为记录样本集合，Xi为样本到实际观测值。

设研究样本指标论域为：

U={u1、u2、u3、...、 un}

单值观测样本点u将其所携带的信息按照式（1）依次扩散到集合U中，

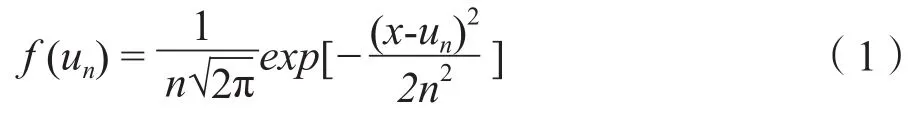
其中：

h—扩散系数。可根据样本最大值b和最小值a及样本点个数m来确定。公式为：

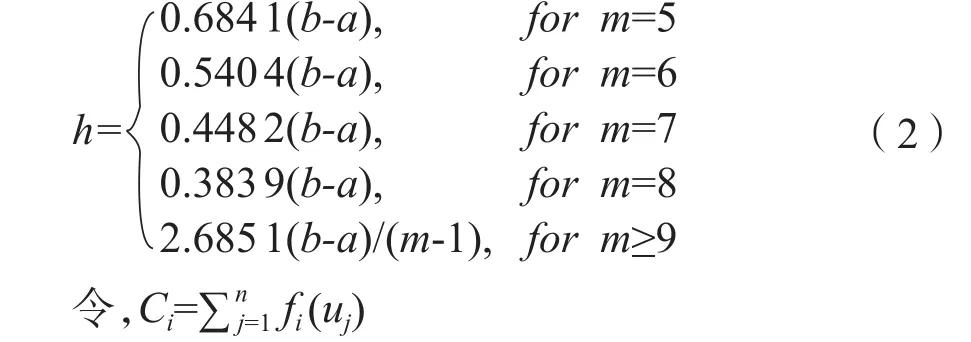
相应的模糊子集的隶属函数是 φxi(uj) =fi(uj) / Cj，称φxi(uj)为样本点Xi的归一化信息分布，对其进行处理，便可得到一种效果较好的风险评估结果。

令，ω(uj) =∑mi=1φxi(uj)

其物理意义是：由{x1、x2、x3、...、 xm}，经信息扩散推断出，如果灾害观测值只能取u1、u2、u3、...、 un中的一个，在将xj均看作是样本点代表时，观测值为φj的样本点个数ω(uj)。显然ω(uj)通常不是一个正整数，但一定是一个不小于零的数。

易知样本点落在uj处的频率值

p(uj) =ω(uj) / ∑nj=1ω(uj)，对于Xi={x1、x2、x3、...、xm}，xj取为论域U中的某一个元素uj。显然，超越uj的概率值应为p (u≥uj) =∑mk=jp(uk)。

2 实例分析

据不完全统计，贵州近12年发生雷电灾害事故1084起，月频分布集中在4~8月，占雷灾总数的85%以上；时频分布主要集中在14~23时，占75%以上。全省以一般雷电灾害事故为主，占历年雷灾总数的73.5%以上；较大、重大雷电灾害事故数相继次之，特别重大雷电灾害事故数为11次，不足1.1%。近12年不同等级雷灾事故数分布，如图1。

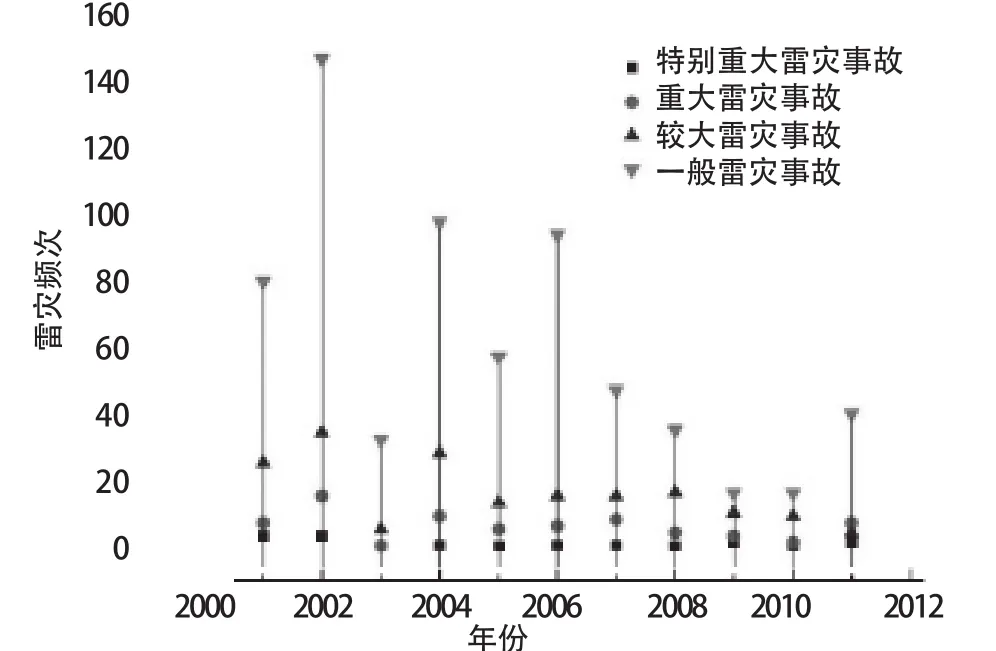
图1 全省近12年不同等级雷灾频数分布

根据全省近12年各等级雷灾频数变化范围，构建特别重大、重大、较大、一般雷电灾害事故的离散论域分别为{0，1，…，5}、{0，1，…，25}、{0，1，…，40}、{0，1，…，200}，按照式（2）确定扩散系数，并将样本按照式（1）扩散至不同等级的雷灾论域中，计算不同等级雷灾对应的不同频次出现的概率，其分布概率、累积概率曲线，如图2。

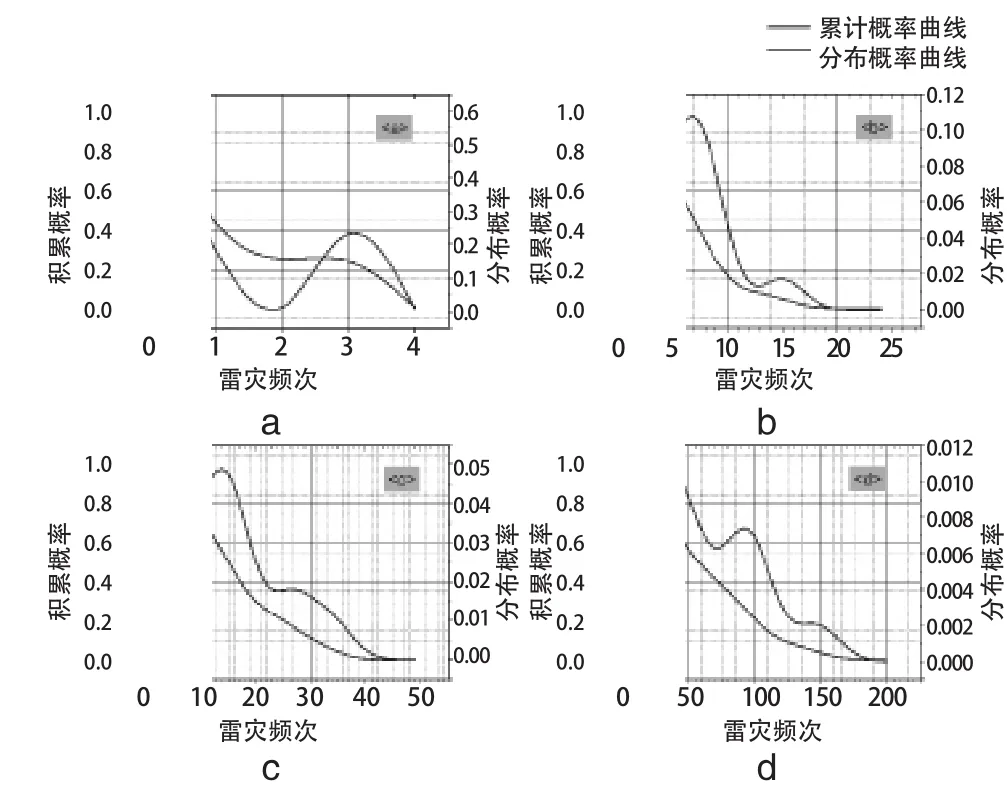
图2 雷灾事故发生概率

图2中的概率表示在各雷灾频次下今后每年中该频次发生的可能性，由分布概率曲线可知：特别重大、重大、较大、一般雷灾事故对应的事故频数集中分布在0-3次、1-7次、2-22次、10-103次，累积风险概率分别达99.2%、77.2%、73.8%、76.8%；峰值分别为0次、7次、14次、34次，发生的可能性分别为0.5687、0.1071、0.0487、0.0108；不发生（0次）的概率分别为0.5687、0.0558、0.0107、0.0037，分别约为2a、18a、90a、270a一遇。

由累积概率曲线，结合下表可知：全省每年特重大、重大、较大、一般雷灾事故数分别超过5次、22次、48次、200次的可能性几乎为零，按照表中的精度可以认为万年难遇。以特重大雷灾事故为例，其风险水平为1次，对应的风险估计值为0.4312，换言之，贵州特重大雷灾事故每年不小于1次的可能性约为2年一遇。

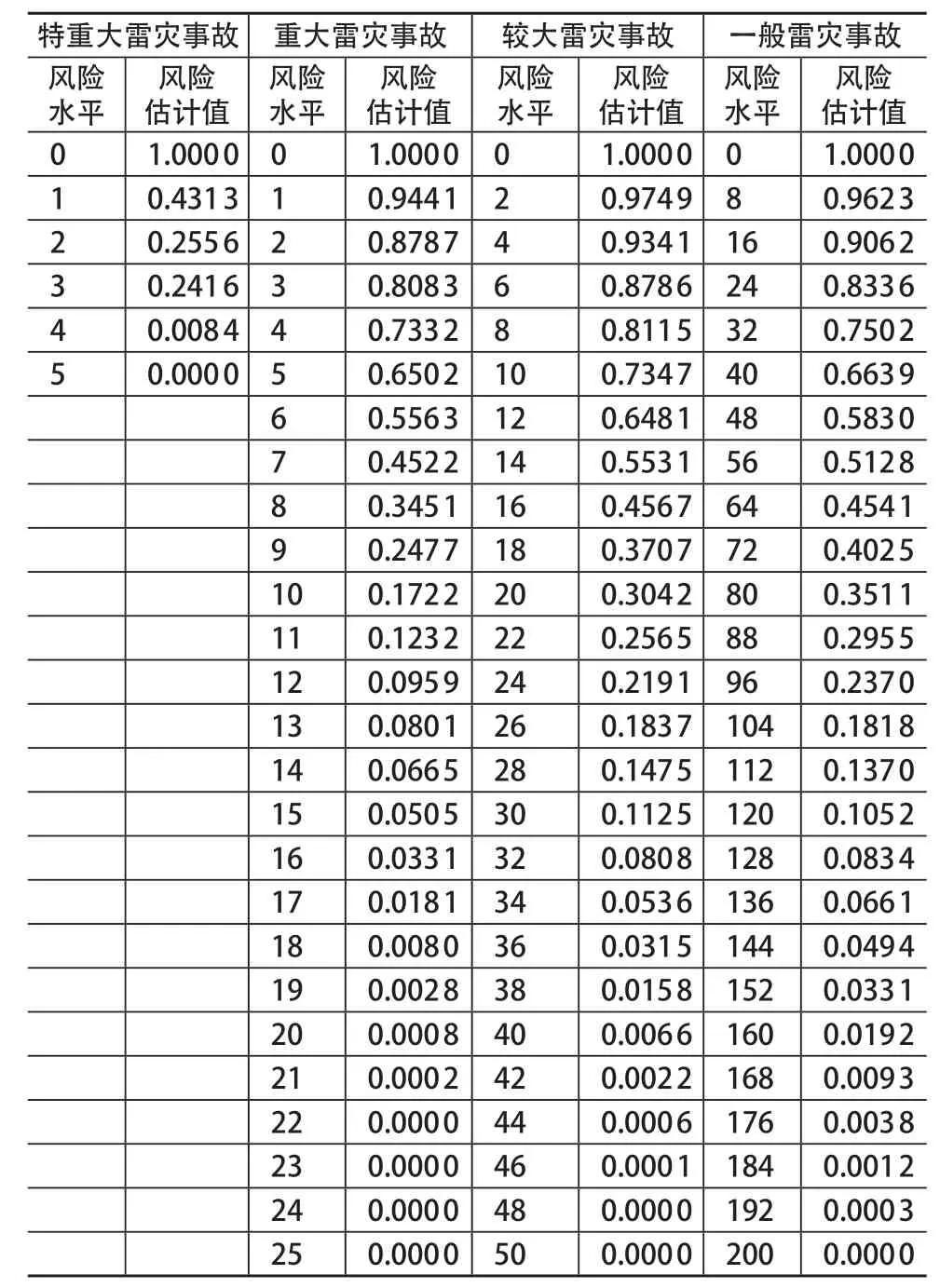
表 不同等级雷灾风险估计值

3 结束语

本文基于信息扩散理论，以贵州近12年历史雷灾资料为背景，预测不同强度等级雷灾事故发生的可能性。在信息缺失或不足的条件下，从样本出发,通过一定的扩散函数来估计母体的概率密度函数，将一个样本点发展成为多个样本点，以扩大样本容量，克服研究过程中面临的历史灾害资料较少、灾害概率分布未知等困难，以提升了结果的合理性。在信息扩散模型的具体运用过程中，对不同类型扩散函数的适用条件及相应的扩散系数的确定将是有待于进一步细化与分析。

参考文献

[1] 张义军,陶善昌,马明,等.雷电灾害[M].北京:气象出版社, 2009

[2] 黄崇福.自然灾害风险评价理论与实践[M].北京:科学出版社,2005

[3] 薛晔,黄崇福.自然灾害风险评估模型的研究进展[A].中国灾害防御协会风险分析专业委员会.中国灾害防御协会风险分析专业委员会第二届年会论文集（二）[C].中国灾害防御协会风险分析专业委员会,2006:10

[4] 刘家福,梁雨华.基于信息扩散理论的洪水灾害风险分析[J].吉林师范大学学报:自然科学版,2009,30(3):78-80

[5] 冯利华.基于信息扩散理论的洪水风险分析[J].信息与控制,2002,31(2):164-170

[6] 张俊香,李平日,黄光庆,等.基于信息扩散理论的中国沿海特大台风暴潮灾害风险分析[J].热带地理,2007,27(1):11-14

[7] 刘引鸽,缪启龙,高庆九.基于信息扩散理论的气象灾害风险评价方法[J].气象科学,2005,25(1):84-89

[8] 张丽娟,李文亮,张冬有.基于信息扩散理论的气象灾害风险评估方法[J].地理科学,2009,29(2):250-254

[9] 储昌超.基于信息扩散理论的区域森林火灾风险预测研究[D].湖南:中南林业科技大学,2014

[10] 全佺,王玲珍,黄成敏.基于信息扩散理论的云南省地震风险评估及管理研究[J].西北地震学报,2006,28(2):180-183

[11] 中国气象局.QX/T 245-2014 雷电灾害应急处置规范[S].北京:气象出版社,2015