标准特征因子的特点与应用分析

■俞立平 李守伟

贵州财经大学贵阳大数据金融学院，贵阳市花溪区花溪大学城 550025

2015年6月18日，汤森路透旗下的知识产权与科技事业部发布《期刊引证报告》（JCR2015），同时发布了两个新的文献计量学指标，一个是标准特征因子（Normalized Eigenfactor，NEI）），一个是期刊影响因子百分位（Journal Impact Factor Percentile，JIFP）。 标准特征因子是华盛顿大学特征因子（Eigenfactor）团队开发的经改进的期刊评价指标，是在特征因子基础上设计的，计算方法是用期刊的特征因子除以同学科其他期刊特征因子的均值。如果某一期刊的标准特征因子为2，这表示该期刊的影响力两倍于同学科领域的期刊[1]。对于标准特征因子的特点、与特征因子的区别以及与其他文献计量指标的关系等等，学术界目前还缺乏关注，因此有必要进行深入研究，以便更准确地应用该指标。

关于特征因子的特点学术界研究比较丰富。特征因子由华盛顿大学的Bergstrom、West等[2]提出，计算时通过构建文献引用网络，考虑到不同层次期刊的引用权重，对期刊的影响力进行评价。Massimo[3]提出了采用特征因子的10个理由，认为其具有立体的数学背景、公理性的理论基础、有趣的随机性解释、以及与其他文献计量指标的有趣关系等特点。Rousseau[4]通过对165种医学期刊的评价研究得出结论，认为H指数与特征因子相关性较强，它们之间的皮尔森系数达到0.951。Waltman等[5]对特征因子和受众因子（audience factor）、影响力（influence weight）进行了比较，研究显示三个指标对不同种类学科以及对影响力小的期刊具有不敏感性。Jacques[6]研究了2001—2008年间的医学类期刊，认为影响因子与论文影响力分值间有很强的相关性。任胜利[7]介绍了特征因子的概念及其原理，比较分析了中外期刊的特征因子分值与论文影响分值，并讨论了特征因子的不足之处。俞立平、隆新文等[8]基于面板数据实证研究发现特征因子和论文影响分值互为高度相关，特征因子与总被引频次正相关，但与即年指标及影响因子无关。郑雅妮、张丛[9]采用类似方法研究经济学期刊发现，影响因子与特征因子之间不存在相关性，二者有不同的侧重点。

从现有的研究看，关于特征因子原理、特点的研究比较成熟，研究视角主要放在特征因子与其他文献计量指标的关系特点以及特征因子的应用上。由于标准特征因子2015年刚刚推出，是个新的文献计量指标，对其进行的相关研究尚处于起步阶段。本文以JCR2015中期刊数量较多的数学与经济学期刊为例，重点比较标准特征因子与特征因子这两个指标的统计学特征，以及其与传统文献计量指标的关系差异，从而进一步了解标准特征因子的特点，并对其应用进行进一步讨论。

1 研究方法

由于特征因子与其他文献计量指标的关系研究比较成熟，标准特征因子是在特征因子基础上产生的，因此为了研究方便，本文重点研究标准特征因子与特征因子的统计学特征差异，以及与其他文献计量指标关系的差异。

从统计学角度，一般文献计量指标的分析视角主要基于区分度与数据分布特点，包括极小极大值比、中位数极大值比、离散系数、数据分布特点等。

从标准特征因子、特征因子两个文献计量指标与其他文献计量指标关系角度，研究方法主要采用回归分析法，鉴于很多文献计量指标的原理均建立在期刊影响力基础上，因此这些文献计量指标之间往往存在着较高的相关性，比如总被引频次、影响因子、5年影响因子、即年指标之间，均是影响力指标。这就容易产生多重共线性问题，使得回归时统计检验不易通过，甚至回归系数符号错误。鉴于研究目的是分析标准特征因子与其他文献计量指标的关系，因此删除相关度较高变量的方法是不合适的，采用面板数据模型也不合适，因为标准特征因子是2015年刚公布的新指标，根本就没有面板数据，所以最好的方法是采用岭回归进行分析。

Horel（1970）[10]提出了岭回归（Ridge Regression）估计方法，它本质上是对传统回归最小二乘法的改进，是一种适用于相关度较高数据回归的有偏的回归方法。岭回归放弃最小二乘的无偏性，以牺牲部分精度为代价来寻求效果稍差但更符合实际的回归结果。

传统的回归是计算：

问题是当存在多重共线性（Multicolinear）问题的时候，向量X′X几乎是奇异（Singular）的，会导致最终估计结果方差非常大。岭回归通过变换向量的特征值来规避这个问题：

这样的估计是有偏的，但是会减少估计方差，如果减少的方差远远大于增加的估计偏差，那么新的方法将是有效的。其实岭回归是一个惩罚回归，用最小化：

来代替最小化：

2 研究数据

本文所有数据均来自于2015 JCR数据库，以学科期刊数量较多的数学期刊为例进行研究，并辅以经济学期刊进行对比。2015年JCR公布的指标中，新指标有标准特征因子、期刊影响因子百分位，其他文献计量指标包括：总被引频次、影响因子、他引影响因子、5年影响因子、即年指标、被引半衰期、特征因子分值、论文影响分值、载文量、引用半衰期、文献选出率。

JCR 2015中数学期刊共312种，由于办刊历史较短和其他原因，部分期刊数据缺失，将其删除后，剩余281种期刊，指标的描述统计如表1所示。

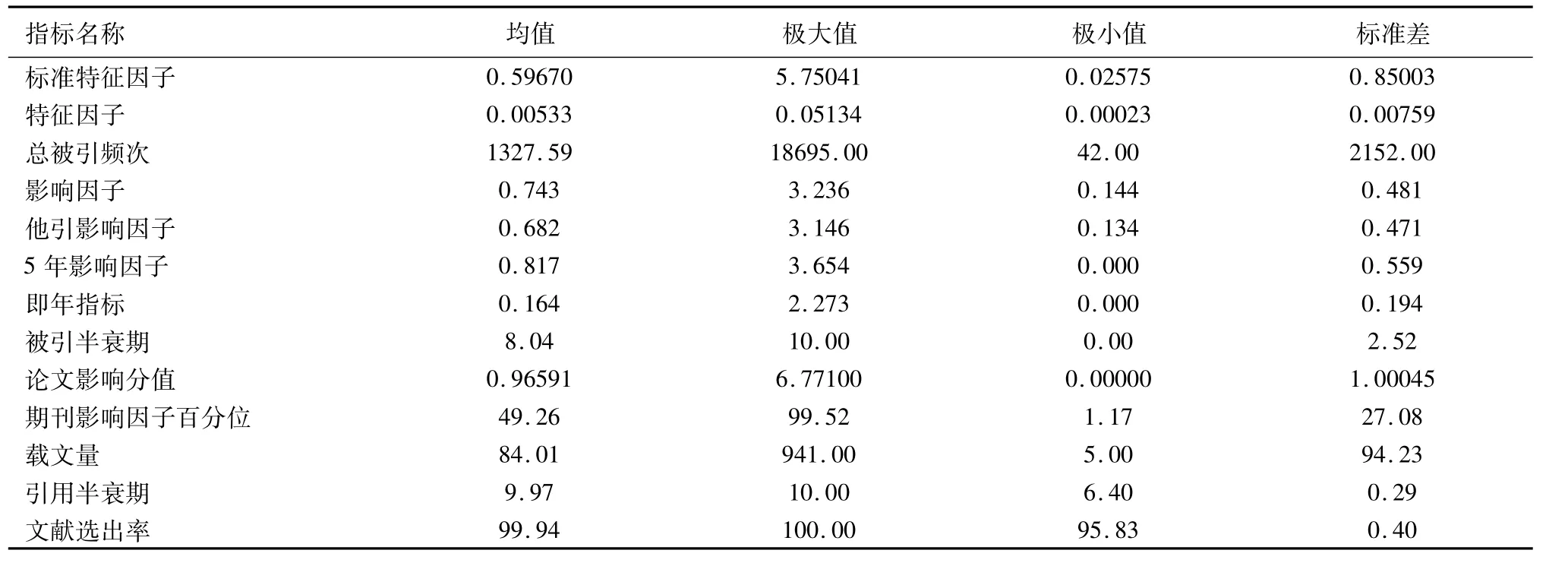
表1 数学学科（JCR2015）文献计量指标描述统计

3 实证结果

3.1 标准特征因子与特征因子的统计学特征分析

标准特征因子与特征因子的区分度与数据分布特点如表2所示。极小值极大值比、中位数极大值比、离散系数基本相同，从数据分布看，无论是偏度、峰度以及Jarque-Bera检验值也基本相同，所以标准特征因子与特征因子的区分度和数据分布基本相同，标准特征因子能够提供的新信息较少。

281种期刊根据标准特征因子的排序结果和根据特征因子的排序结果完全一致。这也进一步验证了标准特征因子与特征因子数据的同质性。

表2 标准特征因子与特征因子的统计学特征分析

3.2 标准特征因子、特征因子与其他指标的关系

标准特征因子与其他文献计量指标岭回归的结果，当岭参数为0.2时，回归基本稳定，回归系数如表3所示。继续进行特征因子与其他文献计量指标的岭回归，发现岭迹图特征几乎一样，岭参数也是在0.2时回归比较稳定，回归结果仍然见表3。

表3 标准特征因子、特征因子与其他文献计量指标岭回归结果

对比标准特征因子、特征因子与其他文献计量指标的岭回归结果，发现拟合优度R2均较高，为0.964，除了他引影响因子由于无法回避的多重共线性系数为负以外，其他回归系数均为正。标准特征因子、特征因子与其他文献计量指标岭回归结果的回归系数基本相同，其绝对值相差均小于15%，同样说明标准特征因子提供的新信息不多。

3.3 标准特征因子与特征因子趋同的原因分析

既然统计学分析与岭回归分析的结论基本相同，下面继续对标准特征因子的内涵特征进行分析。标准特征因子是对特征因子做的一种特殊的标准化，其均值为1，这样标准特征因子超过1的就说明超过了均值，比如标准特征因子为5，就说明该期刊5倍于平均值[11]。但是这种数据标准化并不是简单的线性变换，所以导致标准特征因子的统计学特征以及与其他文献计量指标的关系非常接近，但绝不相同。为了比较这种差异，本文用标准特征因子与特征因子的比值进行学科之间的比较分析，除了数学学科外，另外选取经济学期刊进行比较。也就是说，对特征因子转换为标准特征因子的参照系进行比较分析，结果如表4所示。

表4 数学与经济学标准特征因子/特征因子结果比较

数学学科与经济学学科相差较大，但作为“模拟”参照系的标准特征因子与特征因子的比值的均值非常接近，由于特征因子在一定程度上可以进行跨学科比较，以上研究表明，标准特征因子可以用来进行跨学科比较。

4 结论与讨论

第一，标准特征因子并没有提高指标的区分度。标准特征因子设计的初衷，是为了展现学科内某一期刊与其他期刊特征因子的差别，如果仅仅从数据大小本身看，标准特征因子差不多将特征因子放大了100倍，不像特征因子那样几乎永远小于0，给人的直接感觉是区分度较大。但是标准特征因子并没有提高评价指标的区分度，其极小值极大值比、中位数极大值比、离散系数与特征因子基本相同。

第二，标准特征因子与其他文献计量指标关系与特征因子相似。标准特征因子与其他文献计量学指标的回归系数与特征因子回归结果基本相同，并且期刊标准特征因子排序与特征因子的排序也基本一致，标准特征因子与特征因子正态分布检验结果也基本相同，说明其数据分布特点一致。

第三，特征因子转换为标准特征的非线性转换是导致以上现象的根本原因。由于这种非线性转换均值为1，从而使标准特征因子更容易被理解，总体上是值得肯定的。另外这种非线性转换总体上是一种数据标准化转换，因此没有破坏期刊的排序，是一种修补式的转换，从而导致标准特征因子与特征因子的特征比较接近。

第四，在期刊评价中建议尽量选取标准特征因子指标。由于标准特征因子与特征因子的统计学特征及与其他文献计量指标的关系比较接近，因此在期刊评价中不宜同时选取标准特征因子与特征因子，只能选取一个指标。标准特征因子因为具有较好的显示度更适合进行期刊评价。

[1] Eigenfactor and normalized Eigenfactor.http：//www.lib.vt.edu/research/metrics/journal/eigenfactor.htm l.[2016-3-12]

[2] Bergstrom C T，West JD，Wiseman MA.The Eigenfactor Metrics[J].The Journal of Neuroscience，2008，28（45）：11433-11434.

[3] Massimo Franceschet.Ten good reasons to use the Eigenfactor（TM） metrics[J].Information Processing and Management，2010，46（5）： 555-558.

[4] Ronald Rousseau.On the Relation between the WoS Impact Factor，the Eigenfactor，the SCImago Journal Rank，the Article Influence Score and the Journal h-index[J/OL].[2016-03-11].http：//eprints.rclis.org/13304/1/Rousseau_Nanjing_conference_contribution.pdf.

[5] Waltman L，van Eck N J.The Relation between Eigenfactor，Audience Factor，and Influence Weight[J].Journal of the American Society for Information Science and Technology，2010，61（7） ： 1476-1486.

[6] Jacques Rizkallah D D.Integrative Approach to Quality Assessment of Medical Journals Using Impact Factor，Eigenfactor，and Article Influence Scores[J].PLoS ONE，2010，5（4）： 10240.

[7] 任胜利.特征因子（Eigenfactor）：基于引证网络分析期刊和论文的重要性[J].中国科技期刊研究，2009，20（3）：415-418.

[8] 俞立平，隆新文，武夷山.特征因子与其他文献计量指标关系研究[J].科研管理，2012（8）：41-47.

[9] 郑雅妮，张丛.影响因子、特征因子与其他计量指标的相关性研究——基于经济学期刊面板数据的分析[J].情报杂志，2014，33（5）：96-100.

[10] Hoerl AE， Kennard RW.Ridge regression： biased estimation for nonorthogonal problems[J].Technometrics，1970，12（1） ：55-67.

[11] NORMALIZED EIGENFACTOR© SCORE.http：//ipsciencehelp.thomsonreuters.com/incitesLive/glossaryAZgroup/g16/9709-TRS.htm l.[2016-05-21]