科技期刊学术影响力综合评价模型与实证

■曾 伟 田时中 田家华

1）中国地质大学（武汉）公共管理学院，湖北省武汉市鲁磨路388号 430074

2）安徽大学经济学院，安徽省合肥市九龙路111号 230601

科技期刊具有独特的功能，是展示科技成果的重要窗口，也是评价科研人员研究能力的重要载体，在科研评价系统中发挥着不可替代的作用，重视期刊评价有利于进一步提高期刊学术影响力［1-2］。从现有研究成果来看，人们重点关注期刊评价指标的确立和评价方法的选择［3］，邱均平等［4］对期刊评价指标体系和定量评价方法进行初步探索，张弘［5］和董敏红［6-7］等运用主成分分析方法对期刊质量和学术影响力进行综合评价，俞立平［8］、何莉［9］、辛督强［10］和吴涛［11］等将因子分析方法运用到期刊影响力综合评价，并进行了实证研究，俞立平、刘莲花等运用TOPSIS方法对期刊质量进行实证评价［12-13］，此外，还有学者利用特征向量和非参数统计思维对期刊质量进行评价［14-16］。前人的成果为本文的研究提供了重要的理论参考，不过，现有的研究只是运用单一评价模型对期刊质量进行综合评价，由于单一评价模型适用范围具有一定的局限性，所得评价结果也有一定局限。如果对单一评价模型进行适当组合，运用组合评价模型进行综合分析，就可以最大限度地利用多种评价模型得出的有效信息，发挥单一评价模型的优点，弥补单一评价模型的不足，使得评价结果更为合理，具有一定的实用性。基于此，文章通过建立科技期刊学术影响力综合评价指标体系，选取18种科技期刊作为评价对象，利用《中国学术期刊影响因子年报（自然科学与工程技术）（2014版）》的数据，对评价结果进行Kendall检验，并建立组合评价模型进行综合评价，探讨组合评价模型在科技期刊学术影响力综合评价中的适用性，得出研究结论，为科技期刊进一步提高期刊学术影响力提供数据参考。

1 评价指标及数据

1.1 评价指标

依据《中国学术期刊影响因子年报（自然科学与工程技术）（2014版）》系列标准，依据简洁性、目的性、全面性和可操作性原则，对评价指标进行优选，剔除了与评价目的不相关的指标平均引文数、引用半衰期、引用期刊数，设立13个评价指标，分别是复合总被引Z1、复合影响因子Z2、复合他引影响因子Z3、复合即年指标Z4、可被引文献量Z5、可被引文献比Z6、基金论文比Z7、被引用半衰期Z8、被引期刊数Z9、他引总引比Z10、互引指数Z11，Web即年下载率（万次）Z12、总下载量（万次）Z13。

1.2 样本数据

依据《中国学术期刊影响因子年报（自然科学与工程技术）（2014版）》中的统计数据，综合考虑正交矩阵性质和评价需要，以自然地理类期刊（18种）为评价样本:地理学报A1、地理科学A2、地理研究A3、中国沙漠A4、地理科学进展A5、干旱区地理A6、湖泊科学 A7、地理与地理信息科学 A8、Journal of Geographical Sciences A9、热带地理 A10、山地学报 A11、Chinese Geographical Science A12、Journal of Arid Land A13、极地研究 A14、Journal of Mountain Science A15、云南地理环境研究A16、盐湖研究A17和Sciences in Cold and Arid Regions A18。指标值如表1所示。

2 单一评价模型及过程

在科技期刊学术影响力综合评价中，是否考虑指标权重对结果的影响以及采取何种方式对指标进行赋权是值得深入研究的命题。依据Gnansounou的研究［17］，均方根法可以用来计算评价目标指数，特点是可以不考虑指标权重对评价结果的影响，而是最大限度保留评价指标特征，进行评价与分析。熵值法是通过评价样本的离散程度进行客观赋权。主成分分析方法（PCA）和因子分析则是通过降维思想抽取主成分和主因子，最大限度地保留指标信息，以此进行综合评价。结合科技期刊学术影响力综合评价特点，选用均方根法、熵值法、PCA和因子分析方法对评价对象进行定量评价，运用Excel和IBMSPSSStatistics 19.0软件进行相关数据处理。

2.1 均方根法

（1）无量纲处理

由于评价指标都为正向指标，运用模糊隶属度函数的效益型指标处理公式对指标值进行无量纲处理，无量纲结果如表2所示。

式（1）中，A（Zij）表示无量纲化后的指标量化值，Zij表示指标原值，Zijmax和Zijmin分别表示指标极大值和极小值。

（2）运用均方根公式计算综合指数

公式（2）中，z′ij为标准化后的指标值，即 A（Zii），j为指标数量，i为期刊种类，计算结果如表12所示。

2.2 熵值法

熵值法是根据各项指标观测值所提供的信息的大小来确定指标权重，对评价指标值进行无量纲化处理，根据线性加权求和函数计算综合得分。由于原始数据皆为正值，无需非负化处理。

表1 自然地理学期刊学术影响力文献计量指标

（1）计算第j项指标下第i个方案占该指标的比重

（2）计算第j项指标的熵值

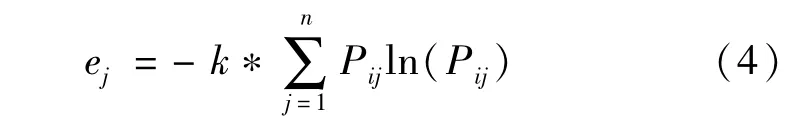
（3）计算差异系数

对差异系数进行归一化即可得到指标权重，结果如表3所示。

表2 指标无量纲结果

表3 评价指标的熵值、差异系数及权重

（4）运用模糊隶属度函数的效益型指标处理公式对指标值进行无量纲处理，无量纲结果如表2所示。依据权重和无量纲结果，按照公式 Fi=Wj*Z′ij（i=1，2，…18；j=1，2，…13） 计算期刊学术影响力综合得分，公式中，wj表示评价指标权重，Z′ij表示无量纲化后的指标量化值，计算结果及排序如表12所示。

2.3 主成分分析法

主成分分析法是利用降维思想把多个指标转化成少数几个指标的多元统计学方法。它能够在保证原始数据信息损失最小的情况下，以少数的主成分取代原有的多维指标变量，既能减小系统变量的数量复杂度，又能保留原系统绝大部分有用信息的特征，使数据结构得到较大程度简化，步骤如下:

（1）评价指标原始数据的无量纲处理，结果如表2所示。

（2）计算无量纲数据的相关系数矩阵R，进行KMO和Bartlett的检验，结果如表4所示。并求相关系数矩阵的特征根即方差贡献率，按照特征值大于1和总的方差贡献率大于80%提取主成分。由表5可以看出，前三个主成分的特征值均大于1，总的方差贡献率83.022%，可以进行主成分分析。

表4 KMO和Bartlett的检验结果

（3）求出主成分矩阵及特征向量。由表6可以看出，在主成分F1上有较高载荷的评价指标是Z1、Z2、Z3、Z4、Z5、Z9、Z12和 Z13，说明 F1基本反映了上述指标的信息。在 F2上指标 Z7、Z8和 Z10有较高载荷。F3上指标Z6和Z11有较高载荷，可以用三个主成分替代原来的13个指标进行综合评价。通过主成分矩阵、初始特征值即可计算主成分矩阵与初始特征值的平方根的比值，即主成分矩阵的特征向量，为了与成分矩阵做区分，特征向量计Ft。如表6所示。

（4）计算评价指标权数。以方差贡献率与总方差贡献率的比值为权数，对主成分矩阵与初始特征值的平方根的比值进行线性加权求和，然后进行归一化，即可得到评价指标的权重。计算求得主成分矩阵的权重系数，如表7所示。

2.4 因子分析法

因子分析是在提取主成分的基础上，通过研究变量之间的相关性，寻求观测数据的结构，并用主因子表示数据的基本结构。所假设的变量基本能够表示原理变量之间的大部分信息。因子分析的基本步骤如下:

（1）将评价指标原始数据进行无量纲处理，如表2所示。

（2）计算无量纲数据的相关系数矩阵R，进行KMO和Bartlett的检验，结果如表4所示。并求相关系数矩阵的特征根即方差贡献率，按照特征值大于1和总的方差贡献率大于80%提取主因子。提取了三个主因子（F1、F2和F3），方差分解及其累计贡献率如表8所示。

（3）求因子载荷矩阵。对3个主因子进行方差极大旋转，得到因子载荷矩阵，如表9所示。

表5 评价指标相关系数矩阵特征根及方差贡献率

表6 评价指标主成分矩阵及特征向量

表7 评价指标权重值

表8 评价指标方差分解及主因子提取分析

表9 正交旋转矩阵因子载荷矩阵及因子得分系数矩阵

由表9可以看出，在主成分F1上有较高载荷的评价指标是 Z1、Z2、Z3、Z5、Z9、Z12和 Z13，说明 F1基本反映了上述指标的信息。在F2上指标Z8、Z10和Z11有较高载荷。F3上指标 Z4、Z6和Z7有较高载荷，可以用3个主成分替代原来的13个指标进行综合评价。

（4）计算因子得分。通过旋转成分矩阵，计算科技期刊学术影响力主因子得分系数矩阵，Fd1、Fd2和Fd3如表9所示。每个科技期刊学术影响力综合得分F为3个主因子的方差贡献率与累计方差贡献率之比分别乘以Fd1、Fd2和Fd3的得分（为方便评价，其得分依然用F1、F2和 F3表示。）得出，表达式如下:

经计算，18种科技期刊学术影响力综合评价得分及排序结果如表12所示。

3 科技期刊学术影响力组合评价模型

3.1 Kendall检验

通过运用均方根法、熵值法、主成分分析方法和因子分析方法对18种科技期刊学术影响力进行综合评价，从结果来看，4种评价方法所得结果具有一定程度的差异。综合来看，可以采用非参数检验方法对评价结果进行一致性检验，如Spearman相关系数检验和Kendall协调系数W非参数检验。此处选择Kendall协调系数进行非参数检验，该方法是用于双因素设计资料的一致性检验方法。其基本原理是b个裁判员对k个观察对象或观察指标进行评分，然后检验b个裁判员的评价结果是否具有一致性。通过IBMSPSS Statistics 19.0软件输出检验结果，如表10和表11所示。

表10 Kendall检验秩均值

表11 Kendall检验统计量结果

表10中的数据表示评价对象的平均秩次。表11显示N为4，表示本次评价的四种方法，Kendall Wa的值为 0.980，卡方值为 66.614，P值（Asymp.sig）为0.000，表明评价结果具有较强的一致性。

3.2 组合模型评价

虽然4种不同评价模型测算的结果整体上比较一致，但也有一定差异，为减少排序差异，克服单项评价模型的不足，借鉴Broda方法对科技期刊学术影响力进行组合评价，该模型综合考虑得分和排序的差异，能够为评价目标服务，基本步骤如下:

（1）求隶属度

Aij表示第i个期刊在第j种评价方法下的得分，μij表示第i个期刊在第j种评价方法下属“优”的程度，即隶属度。

（2）求模糊频数

（3）通过对模糊频数进行归一化处理，得到模糊频率

（4）得分转换

Qhi-j表示第j种评价方法下期刊i排在 h位得分。

（5）求组合评价得分

并按照Fi大小对期刊学术影响力进行排序，其值越大，期刊影响力越大。具体排序及得分结果如表12所示。

4 结果分析

总体上看，单一评价模型得出的评价结果具有一定的差异，具体的说，均方根法与熵值法得出的评价结果差异较大，期刊A6的最大序差达到5。熵值法评价结果与主成分分析和因子分析的结果最大序差为3。主成分分析和因子分析法得出的结果基本一致，只有期刊 A6、A9、A12、A16、A17、A18 存在差异，序差为1。

表12 科技期刊学术影响力单项综合评价与组合评价得分及排序

从组合评价模型的结果来看，组合评价结果与均方根法相比较，有11个期刊排序不一致，最大序差为3。与熵值法比较，也有11个期刊排序不一致，最大序差为3。与主成分分析结果相比较，期刊A12、A16、A17、A18 排序不一致，最大序差为 1。 与因子分析结果比较接近，只有期刊A6和期刊A9排序不一致，序差为1。

与国际通行的总被引频次和复合影响因子评价指标排序比较，组合评价结果排序与复合影响因子排序比较接近，但与总被引频次排序差别较大。

5 讨论

（1）单一评价模型的评价结果均通过了非参数检验，表明四种单一评价模型具有一致性，可以为科技期刊学术影响力综合评价服务，但从模型的适用性上看，因子分析法最佳，主成分分析法次之，熵值法适用性较差，均方根法不太适合用来评价科技期刊学术影响力。

（2）模糊Borda组合评价模型综合考虑了各种评价方法的得分差异和排位次序的不同，使得评价结果与国际通用的复合影响因子评价指标较为接近，运用模糊Borda组合评价模型对科技期刊学术影响力进行综合评价能够得到科学可信的评价结果，该模型具有适用性。

（3）对科技期刊学术影响力进行综合评价，需要对评价指标进行客观赋权，使得评价结果更为科学可信。科技期刊学术影响力评价指标中，复合总被引、复合影响因子、复合他引影响因子、复合即年指标、被引期刊数、互引指数、Web即年下载率和总下载量对科技期刊的学术影响力综合得分影响较大，建议科技期刊着力提高上述评价指标的分值，扩大科技期刊的学术影响力。

（4）本文基于多层次多目标指标体系，运用单项评价模型和组合评价模型得出的结论还有待实践的进一步检验。选择合适的评价指标、建立科学的评价模型对科技期刊学术影响力进行综合评价，仍然是一个值得深入研究的课题，只有不断完善评价体系和评价模型，才能推动科技期刊可持续发展，促进科技期刊学术影响力的进一步提高。

［1］ 赖茂生，屈鹏，赵康.论期刊评价的起源和核心要素［J］.重庆大学学报（社会科学版），2009，15（3）:67-72.

［2］ 叶继元.学术期刊质量评价与核心期刊评价之异同［J］.图书情报工作，2009，53（18）:5-7+16.

［3］ 田昊，贾玉文.4种期刊评价工具的比较研究［J］.情报理论与实践，2007，30（6）:821-824.

［4］ 邱均平，张荣，赵蓉英.期刊评价指标体系及定量方法研究［J］.现代图书情报技术，2004（7）:23-26.

［5］ 张弘，赵惠祥，刘燕萍，陶文文.基于主成分分析法的科技期刊评价方法［J］.编辑学报，2008，20（1）:87-90.

［6］ 董敏红.基于主成分分析的图书情报类核心期刊评价指标有效性研究［J］.情报科学，2010，28（11）:1670-1672+1678.

［7］ 董敏红，杜子芳.主成分分析综合评价应该注意的问题［J］.统计研究，2013，30（08）:25-31.

［8］ 俞立平，刘爱军.主成分与因子分析在期刊评价中的改进研究［J］.情报杂志，2014，33（12）:94-98.

［9］ 何莉，董梅生，丁吉海，等.安徽省高校自然科学学报学术影响力综合评价分析——基于因子分析法［J］.中国科技期刊研究，2014，25（3）:427-431.

［10］ 辛督强，韩国秀.因子分析法在科技期刊综合评价中的应用［J］.数理统计与管理，2014，33（01）:116-121.

［11］ 吴涛，杨筠，陈晨，等.基于因子分析法的科技期刊引文综合评价指标研究［J］.中国科技期刊研究，2015，26（2）:205-209.

［12］ 俞立平，潘云涛，武夷山.TOPSIS在期刊评价中的应用及在高次幂下的推广［J］.统计研究，2012，29（12）:96-101.

［13］ 刘莲花.基于距离综合评价法的数学核心期刊评价［J］.中国科技期刊研究，2015，26（8）:871-874.

［14］ 许海云，方曙，付鑫金.基于特征向量中心度加权的期刊影响因子研究［J］.情报理论与实践，2011，34（11）:108-112.

［15］ 李超.引用质量加权影响因子评价学术期刊研究——以CSSCI图书情报学期刊评价为例［J］.大学图书馆学报，2012，30（1）:29-34.

［16］ 许海云，方曙.非参数统计的期刊影响力评价方法研究［J］.图书情报工作，2013，57（5）:107-113.

［17］ Gnansounou E.Assessing the energy vulnerability:Case of industrialised countries［J］.Energy Policy，2008，36 （7）:3734-3744.