我国股票与基金市场收益和风险的对比分析——基于CEEMDAN
林 达, 杨招军
(湖南大学 金融与统计学院,湖南 长沙 410079)
我国股票与基金市场收益和风险的对比分析
——基于CEEMDAN
林 达,杨招军
(湖南大学 金融与统计学院,湖南 长沙 410079)
摘要:本文基于完全自适应集合经验模态分解(CEEMDAN)和希尔伯特谱分析,对沪深300指数(000300.SH)和主动偏股型开放式基金指数(H11022.CSI)进行了趋势分解和不同时间尺度的波动分析,研究对比了我国股票和基金市场的收益和风险。结果表明:我国基金市场的期望收益率远比股票市场高,风险却小于股票市场。随后解释了出现这种现象的现实原因,并为我国投资者提供了操作上的建议。
关键词:完全自适应集合经验模态分解;希尔伯特谱分析;收益;风险
1引言
投资界通常把基金定义为相对于股票风险较低、收益也较低的稳健资产,它募集投资者的资金,交由专业的投资经理统一管理,是一种利益共享、风险共担的集合投资制度。自推出以来,因无需耗费投资者自身精力打理资金,以及基金经理高水平的投资和风险管理策略,广受普通投资者的欢迎。资深的投资界人士也往往推荐普通投资者通过购买优秀的基金经理所管理的基金间接进入股市,而非自行操作。
对此不少人持有异议,有人认为相比股票,基金虽然风险相对较小,但收益率很不理想、资产增值速度太慢,其中最为著名的是号称“股神”的沃伦·巴菲特,他极力反对投资于采用主动管理策略(包括杠杆和衍生品的使用)的对冲基金,主张普通投资者购买标普500指数型基金,享受股票市场的平均收益率,达到最终战胜绝大部分对冲基金的效果,并于2007年末与对冲基金总裁特德·塞德斯以100万美金为赌注,比较10年后谁的投资策略收益率更高;2015年2月12日,特德·塞德斯因收益率落后过多而提前认输。同时,近年我国频发的基金老鼠仓、利益输送事件,重挫了基金投资者的信心,令投资者不禁产生怀疑:所谓专业的基金经理,其投资策略是否真的高明?
然而,以上两种观点本质上都只是经验之谈,严谨的结论必须通过有代表性的数据和科学的分析工具得出。金融时间序列领域内建模方法有很多:Box和Jenkins[1]提出自回归滑动平均混合模型(ARIMA),预测经济运行短期趋势准确率较高,可以把非平稳序列平稳化;Engle[2]提出自回归条件异方差模型(ARCH),能较好地模拟时间序列变量的波动性变化,Bollerslev[3]将其拓展为广义自回归条件异方差模型(GARCH),以便对误差方差进一步建模;Harvey等[4]把资产定价理论中的扩散过程引入计量经济学,提出随机波动模型(SV),更好地拟合了金融市场的波动特征。但这些模型都建立在一定的假设前提之上,在真实时间序列的实际运用效果并不佳,容易遗漏某些重要现实特征,参数估计亦较为复杂,随后发展起来的上述模型的各种衍生改进模型(形如GARCH-M[5]、GJR[6]、EGARCH[7]、FIGARCH[8]),也治标不治本。此外,计量经济学者普遍采用的差分求对数收益率法,受到混沌经济学者[9]的批评,因为这种方法会破坏系统可能具有的混沌特性。
因此,本文决定使用一种专为非线性非平稳序列而生的时间序列分析方法——希尔伯特黄变换(Hilbert-Huang Transform,HHT),该方法的优点有:算法简单,延迟性低,保留了非平稳序列在不同时间尺度上的特性,能将真实时间序列自适应地分解为若干个本征模态函数(Intrinsic Mode Function,IMF)和一个趋势项,把一个复杂序列简化为几个简单序列分而治之。本文通过这种方法,结合2003年至2015年的实际数据,对我国基金市场和股票市场的收益和波动进行研究、对比,力图呈现与传统方法不同的另一视角,为投资者提供参考、借鉴。
2希尔伯特—黄变换
在本节,我们将介绍后文实证所要用到的分析工具:Hilbert-Huang Transform。

在黄锷提出Hilbert-Huang Transform(HHT)之后,希尔伯特变换的优势才真正开始体现。它发明了一种专门针对非线性、非平稳过程,自适应、后验的(即基于数据、源于数据)数据预处理方法——经验模态分解(Empirical Mode Decomposition,EMD)[10]:对于某个时间序列X(t),如果其过零点个数与极值点个数相等或只相差1,并且极大值包络线与极小值包络线的均值为0(实际操作时只需小于某个很小的正数即可),则X(t)是平稳的,被称为本征模态函数,否则,需要对X(t)进行EMD,具体步骤为:
第一步找出所有极大值点,用三次样条曲线连接起来形成包络线,极小值点同理。并且求出上下包络的均值,得到平均包络m1。
第二步将原序列减去m1,得到h1(t)=X(t)-m1,若h1(t)满足本征模态函数的特征,则得到第一个IMF(本征模态函数),否则,将h1(t)视作新序列重复第一、第二步,直到其满足,我们将第一个IMF记为c1(t)。
第三步用原始时间序列减去c1(t),得到留数r1(t)=X(t)-c1(t)。
第四步对r1(t)进行上述平稳化处理,得到第二个本征模态函数和留数r2(t),以此类推,直到无法从rn(t)继续提取本征模态函数为止。
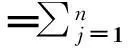
然而,这种方法在处理某些信号时,会出现模态混叠(Mode Fixing)问题,为了解决这个问题,黄锷于2009年提出了一个改进算法——集合经验模态分解(Ensemble EMD,EEMD)[11],其思想是重复对原始时间序列进行EMD,每次进行前加入不同的轻微白噪声,将多次实验的结果取平均数(在消除模态混叠问题的同时抵消引入的白噪声)得到最终结果。Colominas等[12]利用一种自适应的噪声生成算法,把EEMD改进成完全自适应集合经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise,CEEMDAN),并将其与EEMD进行了对比分析。实践表明,CEEMDAN能有效避免模态混叠效应,提高信号分解的准确度。
3实证分析
为了客观反映我国股票市场和基金市场的收益和波动,我们选取了沪深300指数(000300.SH)和主动偏股型开放式基金指数(H11022.CSI)分别代表股票和基金市场的整体情况,以便进一步衡量和研究我国股市的平均收益和基金管理者的平均水平。
3.1两大指数的完全自适应集合经验模态分解


由于股市的运动非常复杂,因此分解出的信号没有严格的周期,只能用引入近似性约化得到的准周期描述。从表1可以看出,无论是沪深300指数还是基金指数分解出来的IMF,其平均准周期越短,则振幅也越小,基金的振幅整体上低于股市(尤其是短期震荡)。振幅指物体振动时离开平衡位置最大位移的绝对值,是表示振动的范围和强度的物理量,与信号能量成正比关系,能量关系到信号的传递距离,具有越高能量、越低频率的信号,衰减过程越长,因此能传播到更远的距离,反之则传播距离有限;振幅越大,在本文中也就意味着金融资产的波动越剧烈,频率越低,则波形越长,意味着金融资产波动的持续性越强,对真实价格走势和投资结果的影响也越大。结合相关系数,可见长时间尺度的分量在股市和基金市场的波动分析中更为重要。值得注意的是,沪深300指数趋势项与真实指数的相关系数是0.47,而基金指数趋势项与原信号的相关系数是0.85,这从另一角度(以往的分析集中于心理层面,认为投资者很不理性)解释了价值投资理念在中国得不到广泛认可并执行的原因:即使从理性角度看,相比代表股市波动的IMF各分量,沪深300的趋势项与真实价格走势的相关系数并没有明显优势(甚至还低于IMF9),也就是说,把握长期趋势未必真地比把握阶段性波动行情重要,所以中国的股票投资者更加倾向于波段操作。相比之下,基金则是非常适合长期持有的投资品。接下来,我们分析沪深300指数和基金指数之间每一个IMF的相关性。
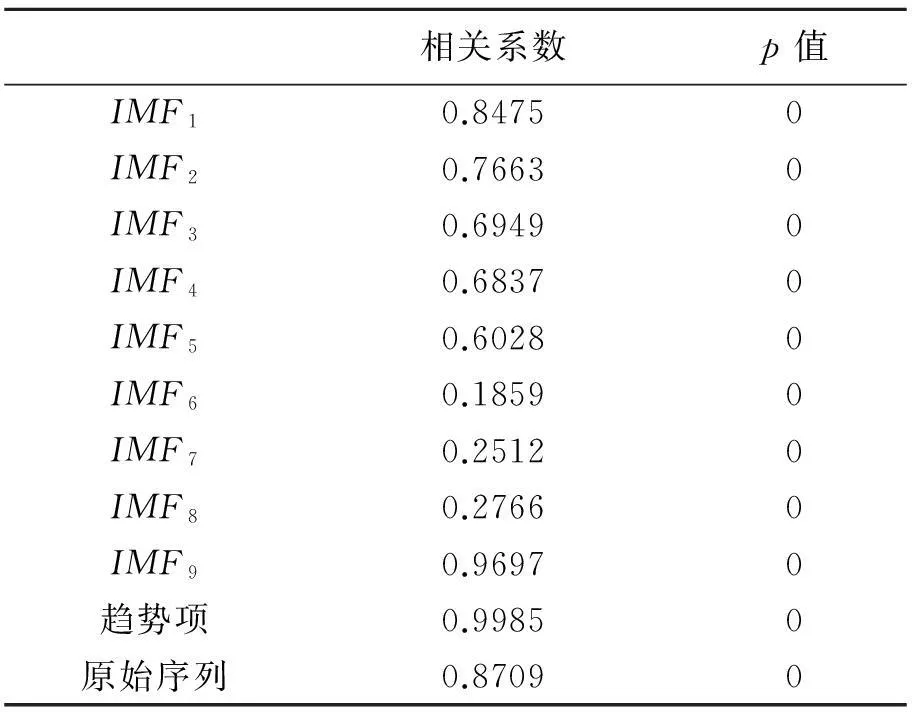
表2 沪深300指数与基金指数之间
根据表2,股市和基金市场之间各IMF的相关系数呈现这样一个特征:最高频和最低频部分相关系数都比较高,而中低频部分相关性则比较弱。就现实而言,从极长远的角度来看,沪深300指数和基金指数都是上涨的,并且股市指数的历史高点往往也是基金指数的历史高位,因此它们之间IMF9和趋势项的相关系数极高;而从短期的角度来看,大盘的短期震荡必然会造成基金净值的起伏(比如某天大盘涨了,基金普遍也会上涨),所以相应的相关系数也较高;至于IMF6~IMF8,由于在单边上涨的行情中,基金经理很难通过精选个股战胜大盘,甚至经常会出现因踏错板块轮动节奏而大盘涨基金跌的局面,而在系统性下跌中,基金受益于良好的纪律性和风险控制意识,通过回避被过度炒作的板块、降低权益投资的仓位、加大固定收益投资的比例,使基金净值的表现优于大盘。同时,我国股市沪深300指数和中小板、创业板指数在某些特定时间段内存在较为明显的“跷跷板效应”,而基金普遍持有较高比例的小盘股,降低了和大盘的同步性,因此造成了中低频部分相关系数较低的特点。
3.2希尔伯特谱分析
在得到沪深300指数和基金指数的本征模态函数后,便可画出时频谱和边际谱,进行希尔伯特谱分析[13],研究原始序列的波动规律。
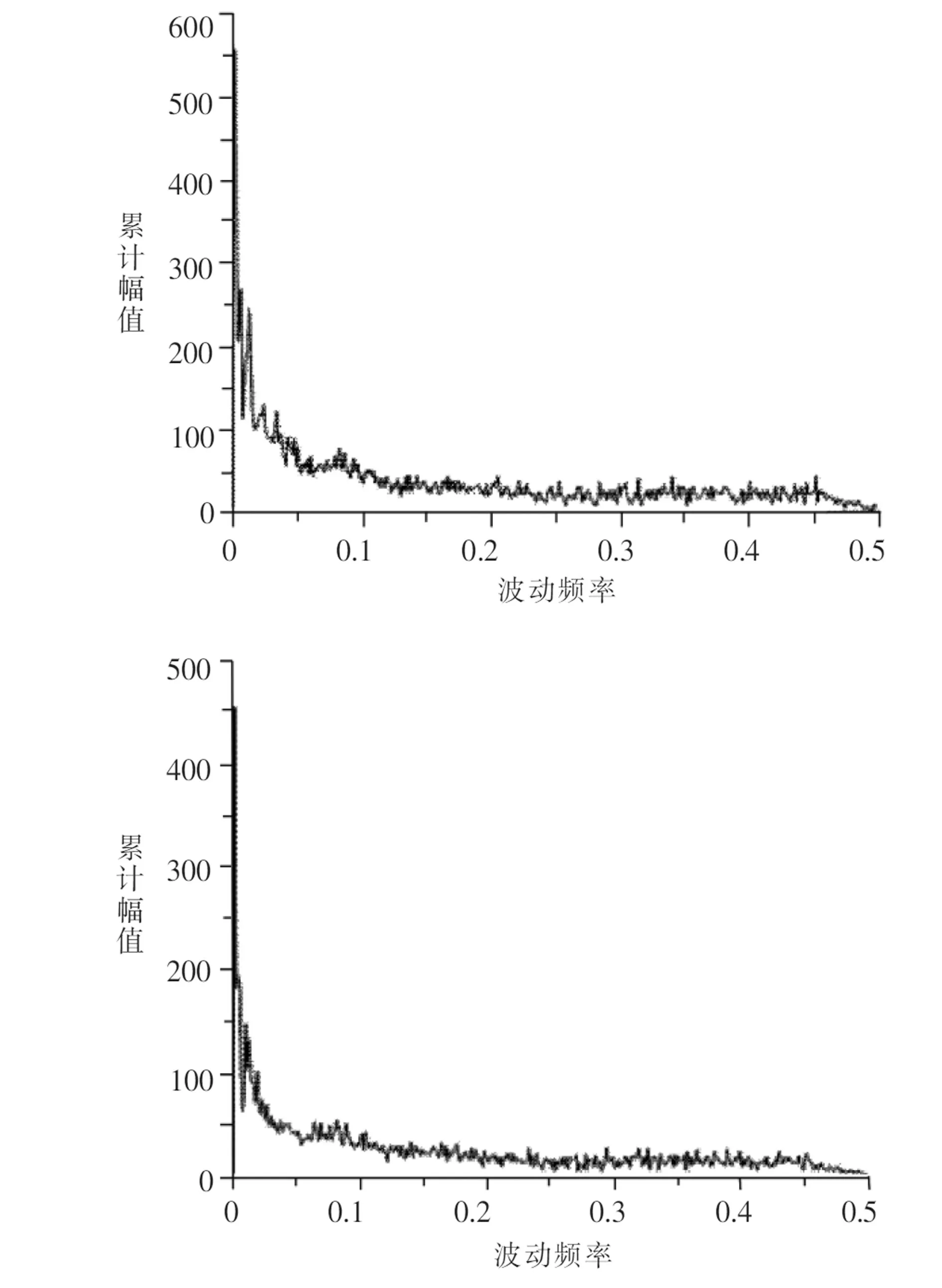
图1 两大指数的边际谱
(受篇幅限制,略去了时频谱)上图对应的是沪深300指数,下图对应的是基金指数,时频谱以颜色的深浅刻画信号能量的时频分布,颜色越深、信号点越密集,代表该频段的信号能量越高。而边际谱则从统计意义上表征了整个时间序列每个频率点的累积幅值分布。以频率为横轴,对应的幅值大小表示此频率波动在各个时刻能量之和的强弱(时频谱给出了该频率波动发生时刻的精确定位)。
根据时频谱,沪深300指数和基金指数的能量分布特征非常相似:能量基本上都散布在低频段,高频段的能量非常低,这一结论符合股市和基金市场的实际波动特征。我们不妨将它们的波动过程分为短期震荡(如短期题材利好、游资投机炒作、坊间传闻等对指数未来走势产生短暂影响、很快就会恢复正常的波动信号)和长期波动(如股权分置改革、四万亿救市等引起长期、深远影响的波动过程),那么短期震荡对未来的影响一般都小于长期波动,原因是频率较低的信号其波形更平稳,走势往往更难以改变,一旦长期波动过程的波形改变,必然是股市大环境的突变造成的,这些突变很可能会导致指数的剧烈震荡,并最终引发大牛市或金融危机。仔细观察边际谱,两指数对应的图形很相似,较明显的差别是在0~0.05频率区间幅值的衰减速度,基金指数大约在0.03(准周期约33个交易日)左右幅值已低于50,而沪深300指数在此处仍有接近100的幅值,到0.05(准周期约20个交易日)才衰减到50左右。这进一步证明了基金的长期投资价值,其波动能量随频率的增高衰减得极快,能量低意味着价格的起伏很小,且稍纵即逝、极难把握,再扣去申购和赎回的手续费,短线波段操作完全无利润可图。
3.3两大指数收益和波动小结
我们给出了沪深300和基金指数的CEEMDAN结果,并进行了相关性分析以及谱分析,得出以下结论:(1)基金的期望收益率高于股票;(2)基金的不同时间尺度的波动整体来说比股票小,走势更稳健,有效地平滑了收益;(3)基金极短期和极长期走势和大盘比较吻合,相应IMF之间的相关系数很高,但有可能因较大的牛市(熊市)而出现特定时间段大幅跑输(优于)大盘的情况;(4)由于基金指数的趋势项与真实走势的相关系数最高,且短期性波动的能量很小、无利润可图,所以操作基金的最佳方式是买入(也可以定投或分批建仓)并长期持有。
4相关现实探讨
从上文的分析结果可以得知,我国的主动偏股型开放式基金无论是期望收益率还是波动率的表现都优于沪深300指数(该指数代表我国股市的平均收益水平)。然而,巴菲特的确赢了这场“史上最昂贵赌局”,且领先优势很明显,那么,为什么本文的结论和此完全相反呢?这是因为我国股市、基金市场和美国的一些显著差异,其中最重要的有三点。
4.1管理费和投资分成的差异
在美国,投资于对冲基金的成本非常昂贵,每年至少要收取2%的管理费和20%的投资分成(部分历史业绩优秀的基金投资分成甚至高达30%、40%),大幅摊薄了基金投资者的利润。在我国,开放式基金每年仅收取1.5%的管理费,无需任何投资分成。我们可以列表分析在不同收费模式下我国主动型开放式基金每年的平均收益率。
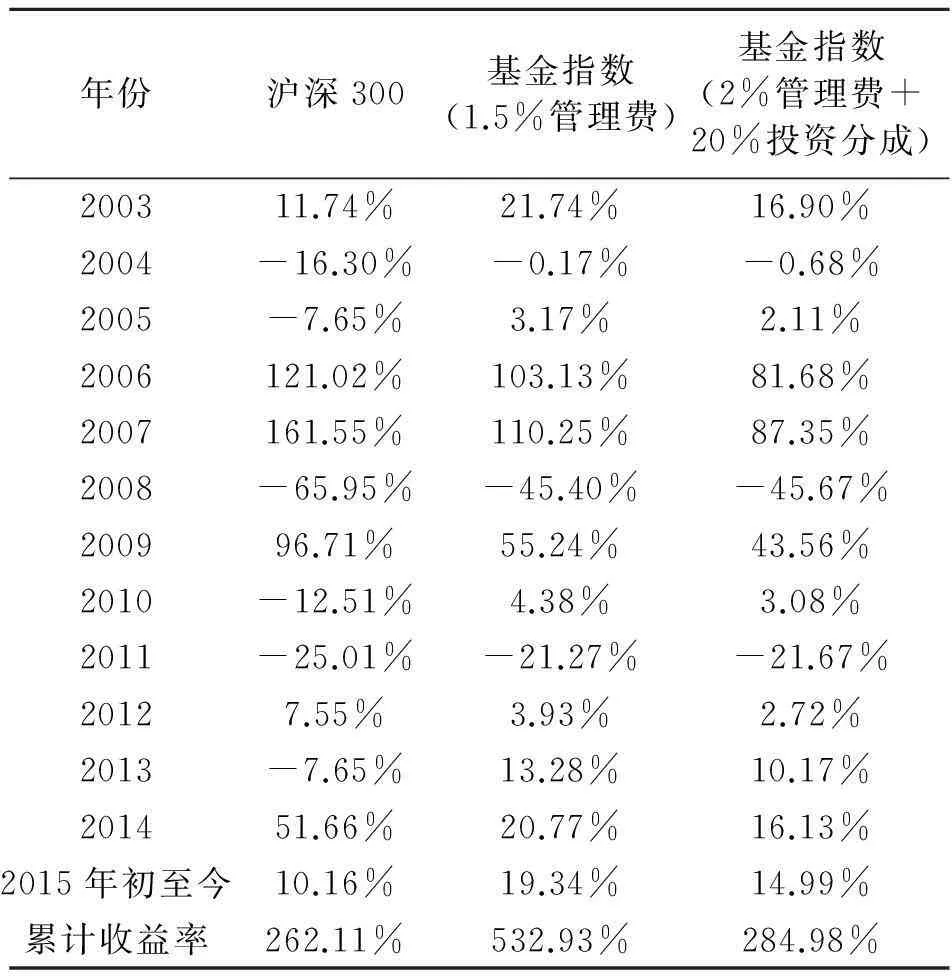
表3 我国主动管理偏股型开放式基金
根据表3,我国的主动管理型偏股基金在过去的12年里确实明显战胜了沪深300指数,假设某人在2003年初用1000元投资了一支未来表现处于平均水平的基金,那么他现在持有的基金价值将会变成6330元;如果当时他把这1000元投资于某支未来表现处于平均水平的股票,那么他现在持有的股票价值是3620元。然而,一旦我国基金采取美国的收费模式,则累计收益率大幅缩减至284.98%,与投资于沪深300指数型基金(被动化投资,旨在获取股市的平均收益)相比已无多少超额收益,基金经理的主动管理价值大大降低。
4.2大盘走势特征的差异
在美国,受益于真实利率的长期下降、企业利润占国民收入比重的持续上升,自1984年以来已经经历了长达30年的牛市,虽然偶尔也有诸如2000年科技股泡沫破裂、2008年金融危机的熊市出现,但每次危机过后反弹更为强劲,比如2009年以来已连续6年大涨。牛市投机氛围较为浓厚,市场风格切换粗暴,基金奉行长期投资,重视风险的控制,投资标的以业绩优秀、增长稳定的股票为主,在单边上涨的市场里容易错失非理性资金推动的行情,同时因为受制于基金契约,以及需留备现金应对赎回要求,所以不可能满仓,最终导致对冲基金多年跑输大盘,渐渐失宠于投资者,费用低廉的指数型基金越来越受到青睐。
相反,中国股市的表现被公认为熊多牛少,大盘走势常年横盘、震荡、下跌,牛市短暂且板块轮动迅猛。基金经理精选优秀个股、严格管理风险等组织性、纪律性的优点得以充分体现,有效地把回撤控制在较低水平,以优质个股创造出高于股市平均水平的收益。
4.3市场有效程度的差异
有效市场假说(EMH)由尤金·法玛(Eugene Fama)于1970年正式提出,法玛把有效市场分为三个等级,弱式有效市场(Weak-Form Market Efficiency)、半强式有效市场(Semi-Strong-Form Market Efficiency)、强式有效市场(Strong-Form Market Efficiency)。市场有效程度越高,能帮助投资者获得超额收益的信息和方法就越少。美国市场如今的制度较为完善,信息公开和金融监管都执行得较为严格,介于弱势有效市场和半强有效市场之间。而我国的市场制度仍很不完善,各方面都有待建设,可能还达不到弱有效市场的标准,机构投资者信息优势极大,内幕交易、股价操纵事件频发,还能参与暴利的一级市场,彻底拉开了与小额投资者(俗称散户)的距离,轻松攫取非正常利润。
以上三个主要原因和其它种种中国金融市场特征,共同造就了一个事实:基金市场期望收益率远高于股票市场,而风险与波动更低。
5结论与启示
本文通过沪深300指数和主动偏股型开放式基金指数的日收盘价数据,借助希尔伯特—黄变换,对我国的股票市场和基金市场的收益和波动特征进行了分析,得出以下结论:
第一,对于我国股票市场投资者(尤其是小额投资者,俗称散户)普遍偏好波段操作、价值投资理念得不到广泛认可并执行的原因,以往的分析一般是强调非理性因素,认为投资者对股市的波动太过敏感,为了股票价格的波动性变化忽视了更为重要的价值中枢长期增长趋势。然而,根据表1,本文认为,即便是从理性角度考虑,由于趋势项和沪深300指数真实走势的相关系数并不高(甚至略低于IMF9),所以长期趋势未必比波动(阶段性行情)重要,波段操作未必不符合理性。但是,基金指数的趋势项与真实走势的相关系数却很高,其长期持有价值凸显。
第二,对于股票和基金之间的比较,相当一部分投资者持有如下观点:基金净值每天的增长幅度很小,若干交易日累计增长幅度尚不如股票涨停一天的收益,所以基金收益率比股票低,增值速度比股票慢。这种观点混淆了极端情况与普遍情况、漂移与随机波动(投资界俗称“账面浮动盈亏”)的概念。衡量金融资产收益高低最科学的指标是期望收益率,但因现实中不易测量,投资界一般采用长期、平均的历史收益率来代替,从表3不难看出,基金市场的平均收益率长期高于股票市场。股票市场短期内可能获取的暴利实际上来源于波动项,而非漂移(漂移才是期望收益的反映),容易在未来的波动中损失殆尽。
第三,从波动率的角度而言,基金指数各个本征模态函数的振幅整体上低于沪深300指数,说明基金的波动率更低、风险更小,有效地平滑了收益流。无论是基金指数还是沪深300指数,其高频分量波动的信号能量都很小,与真实价格走势的相关系数极低,图形特征与白噪声相似。因此,即使是信奉波段操作的趋势投资者,也不宜过于频繁地进行交易,而应适当放弃难以把握的短期震荡价差,专注于更大更深远的波段。
第四,我国开放式基金收益率高于股票、风险却反而更低,这种与发达国家资本市场相悖的现象主要由以下原因产生:(1)我国开放式基金收费低廉;(2)我国股市牛市所占比例较低;(3)信息披露机制的不完善以及一级市场的门槛,导致某些机构投资者拥有轻松超越市场平均收益率的方法。
综上所述,对处于资本市场劣势地位的广大中小投资者而言,主动管理型的基金是股票的完美替代品,且最佳的操作方式是买入(包括定投、分步建仓)并长期持有。
参考文献:
[1] Box G E P, Jenkins G M. Time series analysis: forecasting and control[M]. San Francisco: Holden-Day Press, 1970. 1-15.
[2] Engle R F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation[J]. Econometrica, 1982, 50(4): 987-1007.
[3] Bollerslev T. Generalized autoregressive conditional heteroskedasticity[J]. Journal of Econometrics, 1986, 31(3): 307-327.
[4] Harvey A, Ruiz E, Shephard N. Multivariate stochastic variance models[J]. Review of Economic Studies, 1994, 61(2): 247-264.
[5] Chou R Y. Volatility persistence and stock valuations: some empirical evidence using GARCH[J]. Journal of Applied Econometrics, 1988, 3(4): 279-294.
[6] Glosten L R, Jagannathan R, Runkle D E. On the relation between the expected value and the volatility of the nominal excess return on stocks[J]. Journal of Finance, 1993, 48(5): 1779-1801.
[7] Nelson D B. Conditional heteroskedasticity in asset returns: a new approach[J]. Econometrica, 1991, 59(2): 347-370.
[8] Baillie R T, Bollersleve T, Mikkelsen H O. Fractionally integrated generalized autoregressive conditional heteroskedasticity[J]. Journal of Econometrics, 1996, 74(1): 3-30.
[9] Chen P. A random walk or color-chaos on the stock market? Time-frequency analysis of S&P indexes[J]. Studies in Nonlinear Dynamics and Econometrics, 1996, 1(2): 87-103.
[10] Huang N E, Shen Z, Long S R. et al.. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995.
[11] Wu Z H, Huang N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1- 41.
[12] Colominas M A, Schlotthauer G, Torres M E, et al.. Noise-assisted EMD methods in action[J]. Advances in Adaptive Data Analysis, 2012, 4(4): 1-11.
[13] Huang N E, Shen Z, Long S R. A new view of nonlinear water waves: the Hilbert spectrum[J]. Annual Review of Fluid Mechanics, 1999, 31(1): 417- 457.
A Comparative Analysis of the Risk and Return between Stocks and Funds——Based on CEEMDAN
LIN Da, YANG Zhao-jun
(SchoolofFinanceandStatistics,HunanUniversity,Changsha410079,China)
Abstract:Based on complete ensemble empirical mode decomposition with adaptive noise, combined with Hilbert spectrum, we decompose the csi 300 index and the open-ended funds index and then analyze their volatility of different cycles in order to compare their risk and return. The empirical results show that the expected return of funds is much higher than that of stocks, while the risk of funds is lower than that of stocks. Finally we explain the reason behind this phenomenon and offer some suggestions to the investors in China.
Key words:CEEMDAN; Hilbert spectrum; return; risk
中图分类号:F830.91
文献标识码:A
文章编号:1003-5192(2016)01- 0055- 07
doi:10.11847/fj.35.1.55
基金项目:国家自然科学基金资助项目(71171078,71371068,71221001)
收稿日期:2015- 04- 07

