资产定价核还原方法的算符表述及其应用——以中国股票市场泡沫诊断为例
林 黎
(华东理工大学 商学院,金融工程研究所,上海 200237)
资产定价核还原方法的算符表述及其应用
——以中国股票市场泡沫诊断为例
林 黎
(华东理工大学 商学院,金融工程研究所,上海 200237)
摘要:传统金融工程技术能够得到风险中性概率,但如果不还原出表征市场风险偏好结构的定价核,无法进一步得到真实概率。围绕定价核的还原研究,近年来出现两类不同的方法:Ross的矩阵法,Carr和Yu的微分方程法。前者求解矩阵最大特征值,后者求解方程最小特征值。本文通过引入状态转移定价算符,探讨这两种方法的内在联系,给出统一表述的还原法:求解定价算符特征方程, 其最大实特征值对应市场贴现率,而特征函数代表各状态下的基准风险溢价水平。作为应用,本文研究了我国2005~2007年股市泡沫下的定价核,估计出各行业的风险补偿和贴现要求,证实了泡沫过程中货币幻觉存在性。
关键词:风险中性概率;定价核还原;股市泡沫;算符特征方程
1引言
资产动态定价的核心问题之一是估计资产未来变化的真实概率。当前流行的方法是在定价核框架下研究此问题。定价核, 也称为随机折现因子[1],其倒数对应着所谓基准计价投资组合在未来的价值[2]。资产定价基本定理表明,对于任何无套利机会的金融市场,必然存在着定价核[3]。以定价核来计价的资产,期望收益率都一致地等于无风险利率,这是因为定价核平衡了各状态间风险溢价的差异[4]。本质上,定价核可视为市场潜在的唯一系统性变动因素,对资产收益与波动的预测也最终可划归为定价核动态性质的确定上。
然而,由于定价核本身不可观测,对定价核的量化在实际中很难操作。一种变通的做法是将其拆解为若干风险因子的线性叠加,通过对风险因子的度量来间接衡量定价核水平,比如Fama-French三因子模型[5]或Mark提出的四因子模型[6],但这样无法保证所选因子的完备性。另一种方法是干脆绕过定价核的确定,利用金融工程技术剥离出的状态价格,然后计算风险中性概率作为资产变化真实概率的预测。但中性概率仅度量了市场对各状态的风险对冲偏好。比如,算出市场下月下跌超过10%的风险中性概率为0.8,而下跌不超过10%的风险中性概率仅为0.01,这一事实仅表明, 相对于后一种情形,市场在整体上更多地愿意去对冲下月下跌10%的风险。此时,为进一步确定真实概率必须明确市场在各状态上的偏好结构,而这又回到定价核的确定上。实际上,用风险中性概率作为真实概率的预测隐含假设定价核与市场状态无关,这过于牵强。
最近,Ross找到了一种将定价核与真实概率从风险中性概率中分离出来的方法,称为“还原定 理”[7]。这一方法建立在离散状态的基础上,用矩阵运算来表达。主要思路是从状态转移价格矩阵解出其最大特征根和特征向量。假设投资者满足Von Neumann期望效用法则,且都运用时间可分、 状态间独立的效用函数来决策,Ross证明了,如果状态驱动因子为离散的齐时Markov链,那么最大特征根刚好就是市场贴现率,而特征向量的分量也恰好可以用来构造出状态转移定价核。由于状态转移价格矩阵为非负实方阵,Perron-Frobenius 定理在此可以保证其实值解的存在唯一性和定价核的非负性[8,9]。同时,Ross的方法还可进一步获得风险中性状态转移概率和真实的状态转移概率。另一方面,Carr和Yu[10]也给出了一套定价核的还原方法,但是此方法建立在连续状态的基础上,用微分方程来表达。该方法以风险中性概率测度下定价核满足的微分方程为基础,将定价核还原转化为求解Sturm-Liouville特征值问题。只要定价核有界,那么Sturm-Liouville方程的最小特征值刚好对应着定价核变动的时间趋势,而方程的特征函数就是定价核的倒数。此时Sturm-Liouville定理可以保证该问题有实值解[11]。该方法与 Ross还原方法非常类似,然而后者需要求解最大特征值,可前者则需要求解特征值,两种不同形式的方法之间的联系与区别尚有待进一步探寻。
本文研究发现,通过引入状态转移价格算符,建立定价核还原的算符表述,可将Ross,Carr和Yu的方法归纳为统一的形式。一方面,Ross的还原法等价于求解一个用有限维状态转移价格算符来表述的特征方程。另一方面,当状态转移过程为连续状态的齐时Markov过程时,状态转移价格算符自然变为微分算符。与此同时,Carr和Yu的微分方程也变形到统一表述法下的算符特征方程形式。由此可见,两种不同的方法仅是不同算符形式的特例,Ross的方法对应矩阵算符,而Carr和Yu的方法对应微分算符。不过,估测矩阵型状态价格转移算符需要首先估计状态定价密度,这通常采用交替最小二乘法 (Alternating Least Square),但估计结果非常不稳定[12]。而估测微分状态价格转移算符是去求解估计状态因子风险中性方程,这方面的方法则相对成熟许多,可参见文献[13~16]。另外,微分方程法的待估参数数量也显著小于矩阵算符的参数数量。因此,本文实证部分将采用微分算符的形式。
国内学者对于定价核的研究在早期多限于理论探讨的范畴,如肖辉和吴冲锋[17],临海和郑振龙[18]的研究。近年来,也出现了一些基于定价核的资产定价实证研究,吴鑫育等[19]的权证定价研究,邹高峰等[20]基于从前景理论的价值函数出发建立的PTCAPM模型,以及张玉龙和李怡宗[21]在分解出流动性特征和流动性风险基础上建立的SDF-LCAPM模型,但这些研究都事先假设好定价核所满足特定的动态行为,没能够用数据说明定价核为何取定为该形式。李仲飞和高金窑[22]在模型不确定的情形下通过一般均衡推导出了定价核的一个潜在形式,但并未见相应的实证结果。直接利用实际数据估计出市场中定价核大小及其行为的研究仍较为鲜见。
2定价核还原方法
2.1Ross的定价核还原方法
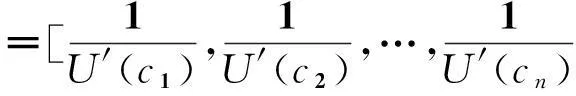
Gφ=δφ
(1)
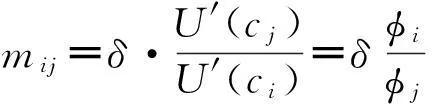
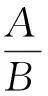
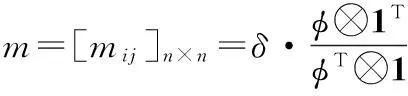
证明首先,从期望效用最优化出发,所解出的Euler方程组可在形式上规简,思路如下
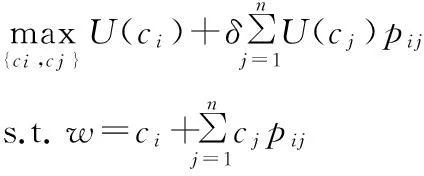
(2)
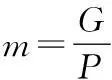
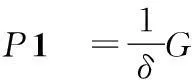
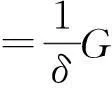
(3)
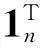
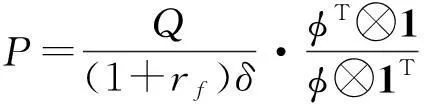
2.2Carr和Yu的定价核还原方法
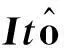
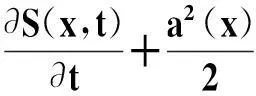
(4)
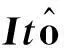
同时φ(x)满足微分方程
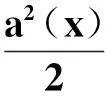
(5)
Carr和Yu发现,上述方程可变形为如下所谓的Sturm-Liouville方程
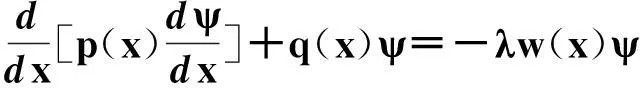
x∈(xmin,xmax),w(x)>0
(6)
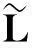
3状态转移价格算符与定价核还原方法的统一表述
由前述讨论可看出,Ross[7]的方法与Carr和Yu[10]的方法在形式上非常不同,前者须求解矩阵 特征值方程获得最大特征值,而后者须求解特征方程获取最小特征值。不仅如此,Carr的方法在推 导时并不事先要求设定投资者的偏好特征。本节将证明,在引入状态转移价格算符Gx后,两种方法实际上服从相同的算符方程,他们只是不同算符设定下的特例。
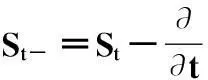
线性算符Gx的含义很明显,未来价格(可视为未来或有价值)通过它变换后恰好是当前的价格,因此它是齐时Markov过程下的定价算符,x对应市场状态。当市场完全且无套利机会时,算符存在且唯一。当市场不完全时,该算符可以有无限多个。
命题2[算符的具体形式]
(1)当x为有n个可选状态的离散Markov链时,算符Gx退化为矩阵[ηij]n×n;

证明根据命题的形式分情况证明,
(1)当x为离散可选状态的离散Markov链时,Hilbert空间变为有限维欧氏空间,St(x)退化为有 限维向量。同时令Gx中的分量ηij表示在t-1时市场处于状态i时能够提供出的状态证券ADij——当未来状态转移到j时就支付 1 元的价格,则算符Gx变为状态转移价格矩阵G。显然,G满足GSt=St-1=St-, 因此GxSt=St-;
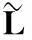
证明先分开讨论Ross的方法与Carr和Yu的方法,最后证明λmax≈1时,两种方法的结果近似相等。
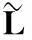
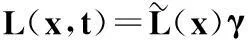
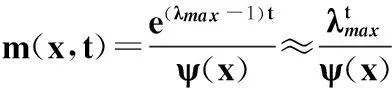
从命题3可以看出,Ross方法与Carr和Yu的还原方法仅是算符形式表述方法在市场不同Markov过程设定下的特例。只要算符为已知,求解算符特征方程即可得到市场内部要求的贴现率, 而特征向量(函数)则反映了状态间的风险调节关系。另外,虽然Carr和Yu的方法未引入效用, 其实风险偏好已隐含在算符Gx中a(x)和b(x)的形式设定上,因为这些参数决定了算符在不同状态上的相对比值,间接表征了市场对于不同状态的偏好程度。需要说明的是,算符形式的表述同样要求市场无套利机会,不过在实际应用时并无需保证市场的完全性,只要设定出驱动市场状态变化的因子即可。
4应用定价核还原法分析股市价格泡沫

我们基于上述提出的微分算符对中国2005~2007年股市泡沫进行了实证。统一选取2005年9月1日作为实证窗口起点,而窗口的终点选为其未来3年内的到达历史最高点交易日的前一天,由于我国此轮泡沫大致在2008年初破灭, 所以绝大多数的窗口终点都集中在2007年9月至2008年1月之间。实证时选取的资产组合为两支市场指数以及27支细分的行业板块指数。我们认为对于泡沫中的每一板块都存在着不同定价核,因为每个板块对应的临界时距演化不尽相同。rf选取为当时的一年期活期存款日利率,数值为0.0081/365≈2.2×10-5。
估计的结果在表1中显示。表中的第5列给出了估计结果所对应的对数极大似然值(相反数),第6列给出的是泡沫膨胀的幂指数,其数值越大表明资产的增值越快,结果显示,在此轮泡沫中的房地产、银行类、煤炭石油、机械、建材、农林牧渔、外贸及有色金属板块泡沫积累速度较高。第10列给出的μτ是τ在真实概率下的时间趋势,表明泡沫破灭的迫近趋势。可以看出,两市股指、房地产、机械指数中的泡沫更快地趋于破灭。表最后两列分别列出了所还原出的定价核φ(τ)的幂指数和市场要求的贴现率,幂指数的绝对值越大代表市场对于临界时点逼近越敏感,即单位临界时距变化上所要求的风险补偿越大。实证结果可见,两市场指数对于泡沫的破灭更为敏感,而行业板块中,较敏感的则是房地产、机械及有色金属板块。同时估计出的市场贴现率均为大于1。这揭示了泡沫中存在着货币幻觉——错置地认为未来的时间价值要更高,因为只要泡沫不破灭,资产增值就将远超无风险利率,交易者们因此会忽略潜在的崩盘损失风险,不急于抛售而更愿意骑行在泡沫上期待未来增值,因此整体上市场更愿意在将来实现变现,更为看重未来的价值。
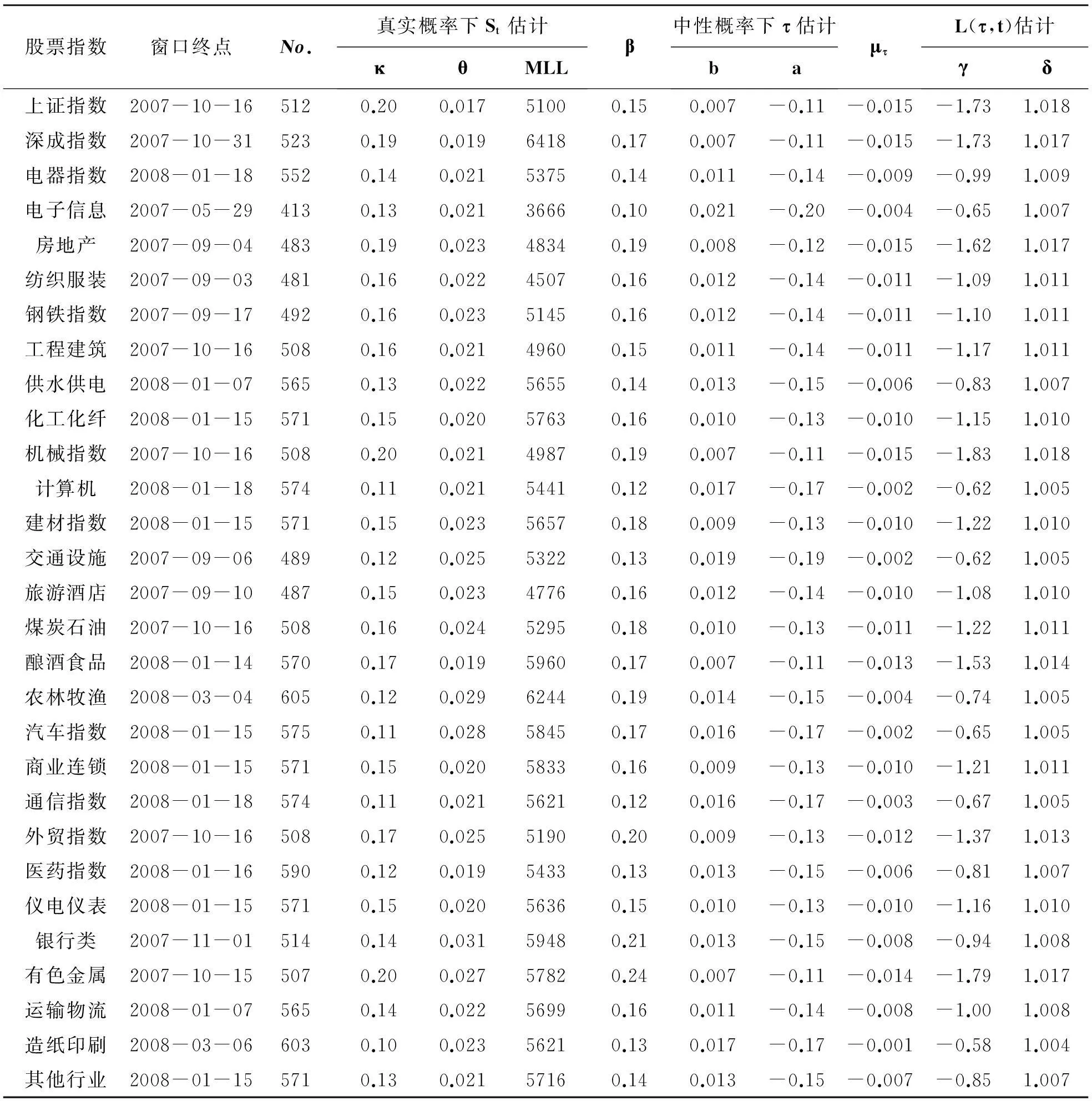
表1 2005~2007年股市泡沫中两市场指数及27个行业板块股指的定价核还原分析
5结论
对于定价核还原方法和技术的研究,在国际上才刚刚起步,本文在梳理和探讨Ross与Carr和Yu不同方法内在联系的基础上,通过引入状态转移价格算符,用算符方程统一了两种方法的表述形式。同时,我们给出了一个将统一表述应用于泡沫建模的例子,通过求解算符特征方程,不仅能够确定资产价格和定价核的运动形式,还可以分析泡沫的膨胀速度并对市场贴现率进行估测从而确定货币幻觉的存在性。
目前,定价核还原方法仅假设市场只由一个状态因子所驱动,从理论上讲,在算符中还可加入其他多个状态因子,此时需要界定每一个状态因子对应适应性条件,由此可得市场的贴现率是各因子对应贴现率的叠加,市场的定价核大小则可通过各因子对应定价核乘积来还原出。无论如何,定价核的还原方法研究还处于相当初步的阶段,很多问题尚待解决。比如,如何将鞅性(无套利)下的方法推广到半鞅甚至更一般的情形;中国市场缺乏充足的衍生工具,如何合理构建状态转移价格算符;如何将行为因素加入算符中,等等。这些问题给后续研究留下诸多机遇与挑战。
参考文献:
[1] Cochrane J H. Asset pricing[M]. Princeton: Princeton University Press, 2005. 1-22.
[2] Bajeux-Besnainou I, Prtait R. The numeraire portfolio: a new methodology for financial theory[J]. European Journal of Finance, 1997, 3(4): 291-309.
[3] Dybvig P H, Ross S A. Arbitrage, state prices and portfolio theory[J]. Handbook of the Economics of Finance, 2003, 1(1): 605- 637.
[4] Duffie D. Dynamic asset pricing theory[M]. Princeton: Princeton University Press, 2010.
[5] Fama E F, French K R. Common risk factors in the returns on stocks and bonds[J]. Journal of Financial Economics, 1993, 33(1): 3-56.
[6] Mark M. On persistence in mutual fund performance[J]. The Journal of Finance, 1997, 52(1): 57- 82.
[7] Ross S. The recovery theorem[J]. The Journal of Finance, 2015, 70(2): 615- 648.
[8] Perron O. Zur theorie der matrices[J]. Mathematische Annalen, 1907, 64(2): 248-263.
[9] Frobenius G. Uber matrizen aus nicht negativen elementen[A]. Sitzungsberichte der Kgl[C]. Preussischen Akademie der Wissenschaften zu Berlin, Berlin, 1912. 456- 465.
[10] Carr P, Yu J. Risk, return, and Ross recovery[J]. Journal of Derivatives, 2012, 20(1): 38-59.
[11] Al-Gwaiz M. Sturm-Liouville theory and its application[M]. Springer Undergraduate Mathematics Series, London: Springer Press, 2007. 67- 88.
[12] Spears T. On estimating the risk-neutral and real-world probability measures[D]. Oxford University MSc Thesis, Oxford, 2013.
[13] Vasicek O. An equilibrium characterization of the term structure[J]. Journal of Financial Economics, 1977, 5(2): 177-188.
[14] Eberlein E, Keller U. Hyperbolic distributions in finance[J]. Bernoulli, 1995, 1(3): 281-299.
[15] Kou S G. A jump-diffusion model for option pricing[J]. Management Science, 2002, 48(8): 1086-1101.
[16] Carr P, Nadtochiy S. Local variance gamma and explicit calibration to option prices[J]. Mathematical Finance, Forthcoming(Accepted), 2014.
[17] 肖辉,吴冲锋.随机折现因子分析[J].工业工程与管理,2004,(3):71-73,110.
[18] 林海,郑振龙.动态风险厌恶,随机贴现因子与资产定价[J].当代财经,2003,(9):5- 8.
[19] 吴鑫育,周海林,马超群,等.基于随机贴现因子方法的权证定价研究[J].中国管理科学,2012,20(4):1-7.
[20] 邹高峰,张维,张海峰,等.中国市场条件下的前景理论资本资产定价模型[J].系统工程学报,2013,28(3):355-361.
[21] 张玉龙,李怡宗.基于随机折现因子方法的流动性定价机制研究[J].管理世界,2013,(6):35- 48.
[22] 李仲飞,高金窑.模型不确定性条件下的一般均衡定价[J].系统工程理论与实践,2012,31(12):2272-2280.
[23] 林黎,任若恩.泡沫随机临界时点超指数膨胀模型:中国股市泡沫的检测与识别[J].系统工程理论与实践,2012,32(4):673- 684.
The Recovery Approach Based on State Transition Pricing Operator Application to the Diagnosing of Bubbles in China Stock Market
LIN Li
(InstituteofFinancialEngineering,BusinessSchool,EastChinaUniversityofScienceandTechnology,Shanghai200237,China)
Abstract:Conventional financial engineering technique only helps one to estimate risk-neutral probability. However, it is impossible to further obtain natural probability without recovering pricing kernel that reflecting the structure of risk aversion preference for the overall market. At present, two kinds of major approaches to recovery pricing kernel are presented, which are respectively matrix-based-method from Ross and differential equation method derived in Carr and Yu. The former relies on finding out the maximum eigenvalue, whereas the later works by searching the minimum eigenvalue. This paper discusses the internal relation-ship between these two kinds of approaches. By introducing the state transition pricing operator, the current two approaches can be uniformed to solve the operator eigenvalue equation, which eigenvalues and eigen-functions respectively indicate the inter-temporal discount rate and the required numeraire risk premium. As an application, the performance of stock bubbles for China between 2005 and 2007 is diagnosed. Except for estimating the risk compensation in different industry, we also confirm the presence of money illusion characterized by distorted discount rate.
Key words:risk-neutral probability; pricing-kernel recovery; stock bubbles; operator eigen-function
中图分类号:F830.9
文献标识码:A
文章编号:1003-5192(2016)01- 0068- 07
doi:10.11847/fj.35.1.68
基金项目:国家自然科学基金青年资助项目(71301051);中央高校基本科研业务费-探索研究基金资助项目(WN1323004)
收稿日期:2015- 01-22

