微型扑翼仿生“0”字和“8”字形扑动方式气动特性研究

张红梅，杨文青

(西北工业大学 航空学院，西安　710072)



微型扑翼仿生“0”字和“8”字形扑动方式气动特性研究

张红梅，杨文青

(西北工业大学 航空学院，西安710072)

摘要：微型扑翼飞行器的气动特性由扑翼的运动规律所决定，为了研究复杂翼梢轨迹对扑翼气动特性的影响，通过对上下扑动、弦向扭转和前后掠动三个自由度的运动设计不同的参数，运用数值模拟方法研究微型扑翼采用仿生“0”字形和“8”字形运动时的气动特性。结果表明：相比于传统的扑动运动，增加了扫掠运动的“0”字形和“8”字形扑动可有效增加升力，特别是“8”字形扑动的增升效果更加显著，但同时也会造成阻力略增，可以通过调整扭转角度来增加推力。本文的研究结果可为复杂运动规律下微型扑翼飞行器设计提供参考。

关键词：气动特性；微型扑翼；仿生扑动；数值模拟

0引言

飞鸟、飞行昆虫、蝙蝠等自然界的飞行生物均采用扑翼方式飞行，尺度缩小后，扑翼飞行是一种可有效提高气动性能的飞行方式。微型扑翼飞行器(Flapping-wing Micro Air Vehicle，简称FMAV)是一种仿生飞行器，但是目前人造的微型扑翼飞行器和飞行生物的飞行能力相比，还相差甚远。

近年来，FMAV受到广泛关注，包括美国、欧盟、日本以及中国在内的世界各国竞相对其展开研究，同时，也得到了诸多研究成果，涉及气动计算、风洞实验等多个方面，揭示了FMAV气动特性的产生机理。K.Viswanath等[1]研究发现下扑过程中若遭遇前向突风，会使升力和推力同时增加；P.Wu等[2]的研究表明某些变形模式可以使推力增加；D.D.J.Chandar等[3]研究发现推力是由对称涡街产生的；S.K.Chimakurth等[4]研究得出展向变形和前缘吸力均有利于增加推力的结论；S.A.Ansari等[5-6]认为较直的前缘有利于升力特性；Y.S.Hong等[7-8]研究表明翼尖涡和展向弯度会对升力产生显著影响。上述研究主要关注了FMAV在扑翼上下扑动情况下的气动特性，目前已有少量文献研究了在扑动运动中增加掠动角度对气动特性的影响。例如，J.A.Esfahani等[9]研究了二维翼型存在掠动运动情况下的气动特性；K.Viswanath等[10]研究了仿昆虫尺度的薄翼型在复杂运动情况下的气动特性，得到了运动与气动特性的对应关系。

微型扑翼飞行器的气动特性完全由扑翼的运动规律决定，自然界飞行生物为微型扑翼飞行器的设计提供了宝贵的借鉴，仿生研究是提高FMAV扑翼飞行能力的一个重要途径。自然界飞行生物的翼稍轨迹并非简单的往复扑动，而是带有一些掠动，使得翼稍轨迹形成不同的曲线。飞行生物的翼稍轨迹如图1所示[11]，常见的有“0”字形和“8”字形。

图1　不同飞行生物的翼稍运动轨迹

本文针对包含前后扫掠的扑动运动的气动特性展开研究，考虑到现有技术条件下仿鸟尺度飞行器具有更强的可实现性，选择仿鸟尺度的微型扑翼为研究对象，通过对其三个自由度的运动设计不同的参数，研究三维扑翼采用仿生“0”字形和“8”字形(为了研究方便，假设理想的“0”字形和“8”字形规律)运动时的气动特性。

1扑动方式定义

按照转轴的不同，扑翼的运动可分为：上下扑动、弦向扭转和前后掠动(以下简称扑动、扭转和掠动)，如图2所示，其中，扑动运动为绕x轴的转动，扭转运动为绕z轴的转动，掠动运动为绕y轴的转动。扑动与扭转被认为是基本运动方式，当加入不同的掠动频率后，扑翼翼稍轨迹将体现出不同的形态，本节将分别定义。

图2　扑翼运动示意图

1.1基本运动

基本运动包括扑动和扭转。扑动运动规律为

ψ(t)=ψmcos(ωt)

(1)

扭转运动规律为

α(z,t)=α0-αm(z)sin(ωt)

(2)

(3)

式中：ψ为在t时间步的扑动幅度；ψm为最大扑动幅度；ω为扑动频率；α为在t时间步的瞬时迎角，也称之为扭转角(包含扭转变形导致的迎角变化)；α0为初始迎角；αm为最大扭转角；z为展向站位；b为半展长。

扑翼按照基本运动规律的运动如图3所示，扭转与扑动的相位差为90°，该相位差下推进效率最高[12-14]。

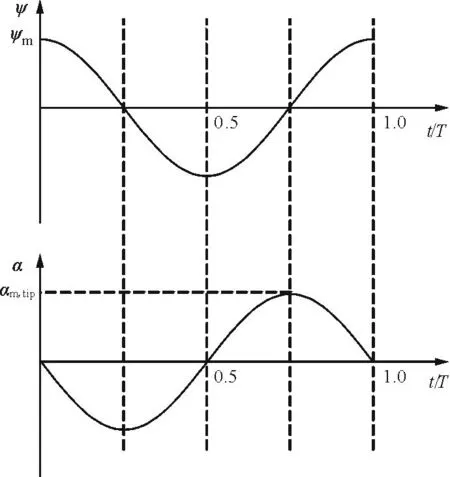
(a) 扑动和扭转的角度函数

(b) 扑动和扭转的运动规律

1.2“0”字形与“8”字形扑动

在基本运动规律上，增加一定的掠动规律，即可形成“0”字形或者“8”字形运动规律，这两种规律的区别在于掠动的频率不同。若掠动频率等于扑动频率，则翼尖轨迹体现为“0”字形；若掠动频率为扑动频率的两倍，则翼尖轨迹体现为“8”字形。当掠动频率更高时，翼尖轨迹则更为复杂，该扑动方式也比较少见，不具有代表性，本文不讨论其影响与规律。

“0”字形扑动运动情况下，掠动角度的变化规律为

β0(z,t)=β0,m(z)sin(ωt)

(4)

(5)

“8”字形扑动运动情况下，掠动角度的变化规律为

β8(z,t)=β8,m(z)sin(2ωt)

(6)

(7)

式中：β*(*为“0”或“8”)为“0”字形或“8”字形运动规律下，t时刻在展向站位z的瞬时掠动角度；β*,m为“0”字形或“8”字形运动规律下，在展向站位z的最大掠动角度；β*,m,tip为“0”字形或“8”字形运动规律下，翼稍最大掠动角度。

“0”字形掠动规律与翼运动示意图如图4所示。

(a) “0”字形掠动的角度函数

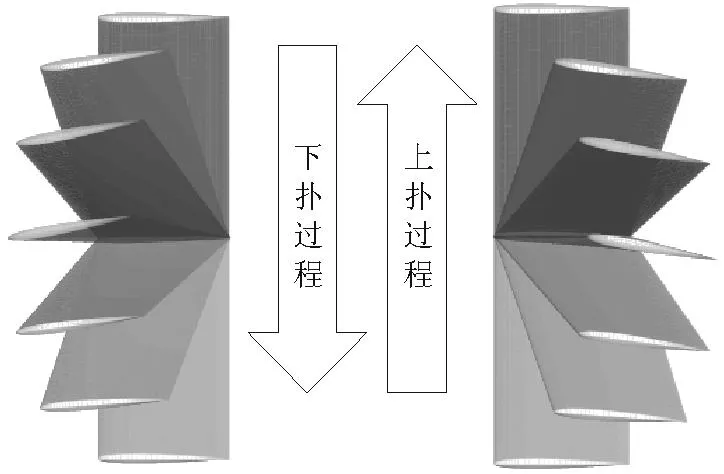
(b) “0”字形掠动的运动规律

“8”字形掠动规律与翼运动示意图如图5所示。

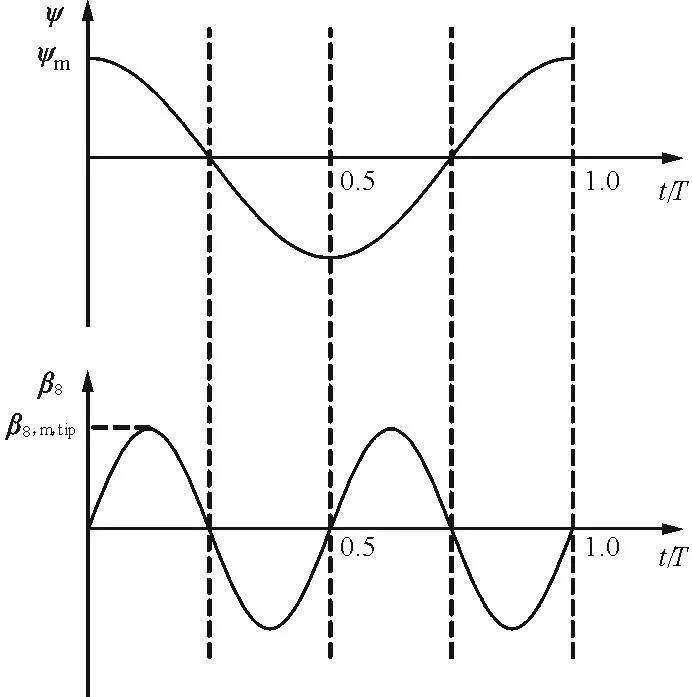
(a) “8”字形掠动的角度函数

(b) “8”字形掠动的运动规律

2数值方法

采用数值模拟方法研究微型扑翼仿生复杂扑动情况下的气动特性。微型扑翼飞行器速度低、尺度小，其绕流具有低马赫数、低雷诺数的特点，受空气粘性的影响很大，故采用雷诺平均N-S(Reynolds-Averaged Navier-Stokes，简称RANS)方程作为基本控制方程[15]。

在连续介质假设下，忽略彻体力和热源的三维非定常可压缩RANS方程可写为如下守恒形式

(8)

其中，

W=[ρ,ρu,ρv,ρw,ρE]T

E=[ρu,ρu2+p,ρuv,ρuw,(ρE+p)u]T

F=[ρv,ρuv,ρv2+p,ρvw,(ρE+p)v]T

G=[ρw,ρwu,ρwv,ρw2+p,(ρE+p)w]T

Ev=[0,τxx,τxy,τxz,βx]T

Fv=[0,τyx,τyy,τyz,βy]T

Gv=[0,τzx,τzy,τzz,βz]T

式中：ρ、(u,v,w)、p、E分别为流体的密度、速度在直角坐标系下的三个分量、压力、单位质量总能。

单位质量总能(E)和单位质量总焓(H)分别为

(9)

H=E+p/ρ

(10)

完全气体的压力和温度状态方程为

p=ρ(γ-1)e

(11)

T=p/(Rρ)

(12)

式中：e为单位质量内能；γ为比热比，对于空气取1.4；R为气体常数。

采用中心格式有限体积法求解积分形式的N-S方程，认为守恒流动变量在网格单元中心，时间推进方法采用显式Runge-Kutta混合多步法和隐式LU-SGS方法，非定常计算采用双时间法。采用预处理方法求解低马赫数下的收敛问题。湍流模型采用SSTk -ω二方程模型。

扑翼计算网格基于嵌套网格方法，该方法不要求各子域共享边界，可有效减轻各区自身网格生成的难度，避免了计算网格扭曲过大、网格疏密分布不合理的状况，非常适合复杂外形或者有相对运动的情况。各个重叠子域的流场解在内边界要求必须光滑，通常由插值来实现，从而得到整个流场的解。洞点识别和插值单元寻址是重叠网格的两个关键技术。本文采用“距离减缩法”[16]高效确定不同网格之间的对应单元，进而快速进行洞点识别，该方法效率高、易于实现，应用于插值单元寻址时，能够快速锁定插值贡献单元。本文所用的数值方法，已经过验证，其过程详见文献[16]。

计算网格如图6所示。

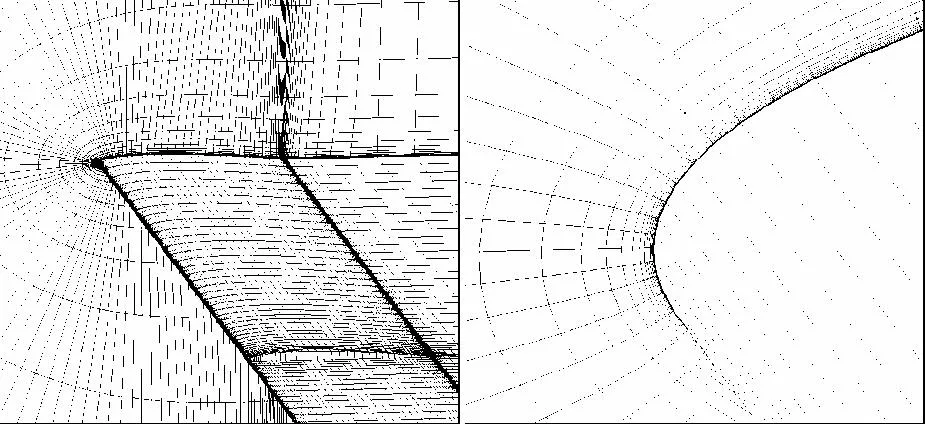
图6　扑翼计算使用的网格

3结果分析

作为基本规律研究，采用半展弦比为4的直机翼，翼型为NACA0008。考虑到仿鸟的研究范畴，取马赫数(Ma)为0.03，雷诺数(Re)为7×104，迎角(α0)为5°，扑动幅度(ψm)为20°，减缩频率(k)为0.2，其余参数详见各小节。

3.1升力和阻力特性

(1) 计算无掠动情况下的气动特性，扭转角变化范围为0°～25°，间隔3°。扭转角变化对升力系数和阻力系数的影响如图7所示。

图7　扭转角对升力和阻力的影响规律

从图7可以看出：当扭转角在18°范围内时，随着扭转角的增大，升力系数和推力系数均增加(即阻力系数减小，因为推力系数和阻力系数为相反数)；当扭转角大于18°时，推力减小。18°是个较大的数值，实际中的扭转角通常不会超过18°，因此，增加扑动时的扭转角可有效增加升力和推力，通过增加扭转角可改变飞行状态，例如改变飞行速度或高度等。

(2) 计算“0”字形扑动运动方式下的气动特性。掠动角度变化范围为0°～20°，间隔2°。“0”字形扑动方式下掠动角度对升力和阻力特性的影响规律如图8所示，可以看出：当掠动角度很小时(小于4°)，增加掠动角会减小升力，但却增加推力；当掠动角度在中等范围时(4°～6°)，增加掠动角会使升力和推力同时增大；当掠动角度继续增加时(大于6°)，增加掠动角度会增加升力，但却减小推力。

图8　“0”字形扑动时掠动角对升力和阻力的影响规律

在“0”字形扑动规律下，掠动角度对气动特性变化规律的影响比较复杂，小范围掠动角的增加对推力有利，而大范围掠动角的增加对升力有利。

(3) 计算“8”字形扑动运动方式下的气动特性。掠动角度变化范围为0°～20°，间隔2°。“8”字形扑动方式下掠动角度对升力和阻力特性的影响规律如图9所示。

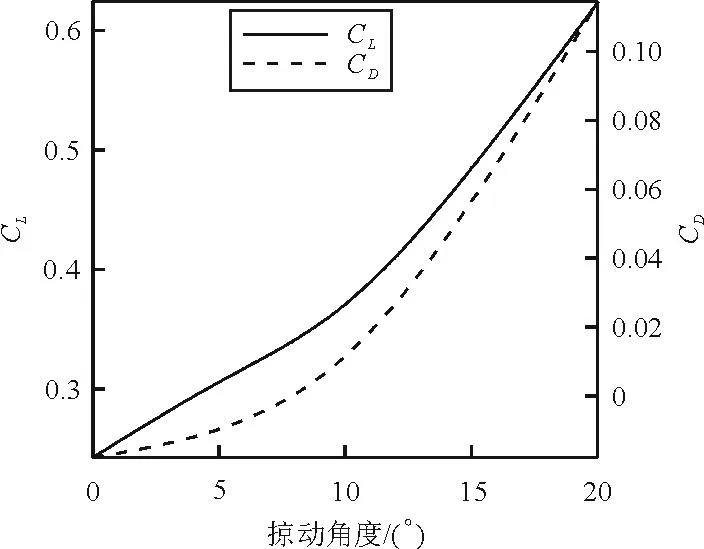
图9　“8”字形扑动时掠动角对升力和阻力的影响规律

从图9可以看出：“8”字形扑动规律下，随着掠动角的增加，升力增加但推力减小；当掠动角度在较小范围变化时(小于7°)，升力的增加比例大于推力的减小比例；当掠动角度在较大范围变化时(大于7°)，升力的增加比例小于推力的减小比例。

“8”字形扑动方式对升力有利，但却以降低推力为代价。

3.2流场分析

展向50%截面处的流场压力云图，如表1所示。

表1　不同扑动方式流场压力变化云图

从表1可以看出:“纯扑动”产生的压力波动范围最大，表明“纯扑动”产生的气动力波动范围也最大；在“纯扑动”过程中，有相当一部分气动力在上扑和下扑的过程中被抵消，造成运动的浪费；“扑动加扭转”的压力波动情况优于“纯扑动”，其压力变化范围减小，且后缘压力增大，有利于增加推力；“0”字形扑动方式在下扑过程中，由于有向前的掠动，增强了升力，但同时也增加了阻力；“8”字形扑动方式由于掠动时速度更快，对升力有较强的增加作用，但同时也显著增加了阻力。

4结论

(1) “纯扑动”的效果很差，“扑动加扭转”的运动方式对升力和推力均有益处，增加掠动运动后主要增加升力，“8”字形扑动方式比“0”字形扑动方式在增强升力方面效果更好。

(2) 从运动机理上讲，掠动运动其本质是在一定程度上改变了扑翼的合速度方向，从而影响了有效攻角，导致不同的气动特性。

(3) 增加扑动时的扭转角可有效增加升力和推力，从而改变飞行状态；通过利用掠动角也可达到增升的目的。

(4) 本文的研究结果可为复杂运动规律的微型扑翼飞行器设计提供了参考。

参考文献

[1]ViswanathK,TaftiDK.Effectoffrontalgustsonforwardflappingflight[J].AIAAJournal, 2010, 48(9): 2049-2062.

[2]WuP,IfjuP,StanfordB.Flappingwingstructuraldeformationandthrustcorrelationstudywithflexiblemembranewings[J].AIAAJournal, 2012, 48(9): 2111-2122.

[3]ChandarDDJ,DamodaranM.Computationofunsteadylowreynoldsnumberfree-flightaerodynamicsofflappingwings[J].JournalofAircraft, 2010, 47(1): 141-150.

[4]ChimakurthSK,TangJ,PalaciosR,etal.Computationalaeroelasticityframeworkforanalyzingflappingwingmicroairvehicles[J].AIAAJournal, 2009, 47(8): 1865-1878.

[5]AnsariSA,KnowlesK,ZbikowskiR.InsectlikeflappingwingsinthehoverpartⅠ:effectofwingkinematics[J].JournalofAircraft, 2008, 45(6): 1945-1954.

[6]AnsariSA,KnowlesK,ZbikowskiR.InsectlikeflappingwingsinthehoverpartⅡ:effectofwinggeometry[J].JournalofAircraft, 2008, 45(6): 1976-1990.

[7]HongYS,AltmanA.Streamwisevorticityinsimplemechanicalflappingwings[J].JournalofAircraft, 2007, 44(5): 1588-1597.

[8]HongYS,AltmanA.Liftfromspanwiseflowinsimpleflappingwings[J].JournalofAircraft, 2008, 45(4): 1206-1216.

[9]EsfahaniJA,BaratiE,KarbasianHR.Fluidstructuresofflappingairfoilwithellipticalmotiontrajectory[J].Computers&Fluids, 2014, 108: 142-155.

[10]ViswanathK,TaftiDK.Effectofstrokedeviationonforwardflappingflight[J].AIAAJournal, 2013, 51(1): 145-160.

[11]ShyyW,LianY,TangJ,etal.AerodynamicsoflowReynoldsnumberflyers[M].UK:CambridgeUniversityPress, 2008.

[12]JonesKD,PlatzerMF.Numericalcomputationofflapping-wingpropulsionandpowerextraction[C].AIAA-97-0826, 1997.

[13]TuncerIH,WalzR,PlatzerMF.Acomputationalstudyonthedynamicstallofaflappingairfoil[C].AIAA-98-2519, 1998.

[14]IsogaiK,ShinmotoY,WatanabeY.Effectsofdynamicstallonpropulsiveefficiencyandthrustofflappingairfoil[C].AIAA-97-1926, 1997.

[15] 韩忠华, 乔志德, 熊俊涛, 等.Navier-Stokes方程预处理方法及其对翼型绕流数值模拟的应用[J]. 西北工业大学学报, 2006, 24(3): 275-280.

HanZhonghua,QiaoZhide,XiongJuntao,etal.Developmentofanefficientviscouspreconditioningmethodanditsapplicationtonumericalsimulationofflowsoverairfoils[J].JournalofNorthwesternPolytechnicalUniversity, 2006, 24(3): 275-280.(inChinese)

[16] 杨文青, 宋笔锋, 宋文萍. 高效确定重叠网格对应关系的距离减缩法及其应用[J]. 航空学报, 2009, 30(2): 205-212.

YangWenqing,SongBifeng,SongWenping.Distancedecreasingmethodforconfirmingcorrespondingcellsofoversetgridsanditsapplication[J].ActaAeronauticaetAstronauticaSinica, 2009,30(2): 205-212.(inChinese)

张红梅(1969-)，女，助理工程师。主要研究方向：微型飞行器。

杨文青(1980-)，女，博士，副教授。主要研究方向：微型飞行器、非定常气动特性。

(编辑：马文静)

Investigation of “0”-Figure and “8”-Figures Wingtip Path Effect on Aerodynamic Performance of Micro Flapping-wing

Zhang Hongmei, Yang Wenqing

(School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China)

Abstract:The aerodynamic performance of flapping-wing micro air vehicle(FMAV) is determined completely by the motion of flapping wings. In order to study the complex wingtip trajectory influence on the aerodynamic characteristics, the “0” and “8” figures effects are investigated by numerical method. The movement is divided into three degrees of freedom: plunging, pitching and swing with different parameters setting. The numerical results show that, compared with the traditional flapping motion, the flapping manners in “0” and “8” figures can effectively increase the lift because of the added swing motion, especially in the “8” figure flapping. However, the drag increased slightly at the same time. The thrust can be increased by adjusting the pitching angle. This study can be provided as a reference for the FMAV design with a complex wingtip trajectory.

Key words:aerodynamic performance; micro flapping-wing; bionic flapping; numerical simulation

作者简介：

中图分类号：V211.3

文献标识码：A

DOI：10.16615/j.cnki.1674-8190.2016.01.007

文章编号:1674-8190(2016)01-044-07

通信作者：张红梅,zhm@nwpu.edu.cn

基金项目：国家自然科学基金(11402208)

收稿日期：2015-10-27；修回日期：2016-01-05

中央高校基本科研业务费专项资金(310201401JCQ01002)