基于贝叶斯统计方法的精细地面灌溉智能控制系统合理数据量研究
吴彩丽,许 迪,白美健,李益农(1.国家节水灌溉工程技术研究中心,北京 100048;2.中国水利水电科学研究院 水利研究所,北京 100048)
地面灌溉是目前我国应用最为广泛的田间灌水方法,但现有地面灌溉田间管理粗放,灌溉过程可控制性差,地面灌溉性能指标值普遍偏低,此问题已成为制约我国地面灌溉技术发展的瓶颈。加强对灌溉过程的控制和管理,对于提高地面灌溉田间管理水平,改进地面灌水质量具有重要的理论和实际意义。精细地面灌溉智能控制技术的原理是在灌溉过程中通过实时采集田块前一部分数据量的灌溉信息估算土壤入渗参数和田面糙率系数,再借助数值模拟手段对整个灌水过程进行预测,从而优化决策出灌溉性能最佳时所需的灌水时间或入畦流量,并根据优化决策方案对灌溉管理参数(灌水时间或入畦流量)实施控制。由于土壤入渗参数的空间变异性,若实时采集的灌溉信息数据量过少,则估算出的土壤入渗参数难以代表田块的整体状况,会给灌溉模拟和优化控制带来较大误差;实时采集的灌溉信息数据量越多,估算出的土壤入渗参数越能代表田块的整体状况,但若采集的灌溉信息数据量过多,则会错过最佳调节时机,难以达到最佳灌溉性能。因此,确定需要采集灌溉信息的合理数据量是根据已知灌溉信息准确预测未知灌溉过程,实现对灌溉全过程控制和管理的首要问题。国内外学者对此进行了一些研究,Clemmens等(1992年)通过对灌溉过程中0%、25%、40%、50%、75%和100%的水流推进数据量采用贝叶斯方法估算土壤入渗参数和田面糙率系数,并将得到的土壤入渗参数和田面糙率系数代入地面灌溉模拟模型,对整个水流运动过程进行预测模拟,将水流推进过程模拟值与实测值之间的平均相对误差进行比较,提出基于水流推进至75%时的数据量进行控制相对合理;董孟军(2010年)对于畦长200 m的田块选取推进距离60,70,80,…,200 m的15组灌溉信息,采用直接法估算土壤入渗参数,并将得到的15组土壤入渗参数代入地面灌溉模拟模型,对整个水流运动过程进行预测模拟,以水流推进过程模拟值与实测值之间的平均相对误差在15%以内,并且与利用全部水流推进数据的平均相对误差之差在10%以内的最短推进距离为原则,提出基于水流推进至60%时的数据量进行控制最为合理。上述学者提出的实施控制需采取的数据量均是根据某一些特定的试验数据得出的经验值,是否具有广适性不得而知,本文拟基于贝叶斯统计方法,从理论上论证精细地面灌溉智能控制系统需采用的能够准确估算入渗参数并预测灌溉全过程的合理数据量。
1 方法与试验
1.1 贝叶斯统计方法
在精细地面灌溉智能控制中,确定不同精度要求所需的合理数据量时用到了贝叶斯统计方法。基于贝叶斯统计方法,将先验信息、样本信息和似然函数相结合推导后验分布及置信区间,从理论上论证精细地面灌溉智能控制需采用的能够准确估算入渗参数并预测灌溉全过程的合理数据量。贝叶斯公式包含了归纳推理的一种思想,贝叶斯统计方法的基本观点是由贝叶斯公式引申而来的。贝叶斯公式是概率论中的一个著名公式,是由英国学者贝叶斯(T.Bayes)在1763年提出来的:设试验E的样本空间为S,A为E的事件,B1,B2,…,Bn为S的一个划分,即某个过程的若干可能的前提,且P(A)>0,P(Bi)>0 (i=1,2,…,n),则:
(1)
式中:P(Bi)是人们事先对各前提条件出现可能性大小的估计,称之为先验概率;P(Bi∣A)既是对以A为前提下Bi的出现概率的重新认识,称P(Bi∣A)为后验概率。
1.2 灌溉模拟模型
采用基于混合数值解法的一维全水动力学畦灌模型(章少辉,2012年)对畦灌水流运动过程进行模拟。所谓混合数值解法,即基于隐-显混合时间格式,利用有限差分法、矢通量分裂与通量差分混合格式(AUSM)有限体积法和有限单元法分别对全水动力学畦灌模型中各矢量项进行空间离散,对形成的3对角矩阵型控制方程代数方程组进行数值求解。
基于混合数值解法的一维全水动力学畦灌模型中采用地表水入渗经验公式中应用最为广泛的是Kostiakov(1932年)入渗公式(z=kta,z为累积入渗水深,mm;k为入渗参数,mm/sα;a为入渗指数,主要取决于土壤质地与结构;t为土壤入渗受水时间,s)描述土壤入渗特性。
模型输入参数为:畦田规格、田面微地形、单宽流量、关口时间、Kostiakov入渗参数及糙率系数。模型输出参数为:灌水效率、灌水均匀度及储水效率等。
一维全水动力学模型方程:
(3)
式中:x为水平向坐标,m;t为水流运动时间,s;h为地表水深,m;g为重力加速度,m/s2;U为沿x水平坐标向的垂向均布流速,m/s;Q为沿x水平坐标向的单宽流量,m3/(s·m);ic为地表水入渗率,m3/(s· m2);b为畦面高程,m;n为曼宁糙率系数,m/s1/3。
1.3 试验田块基本信息
1.3.1先验信息
设先验信息来自按畦长不同选取的大兴(12个田块冬灌、春灌)、河北鹿泉(10个田块冬灌)和山东无棣(8个田块冬灌、春灌)3个试验区的50组典型田块的历史灌溉资料,典型田块基本信息见表1。实测灌溉资料主要包括田块规格、田面微地形、灌溉开始和关口时间、灌溉水流推进过程、入畦流量等,田面微地形和水流推进消退时间的测点间距为5 m。

表1 先验信息田块灌溉基本资料
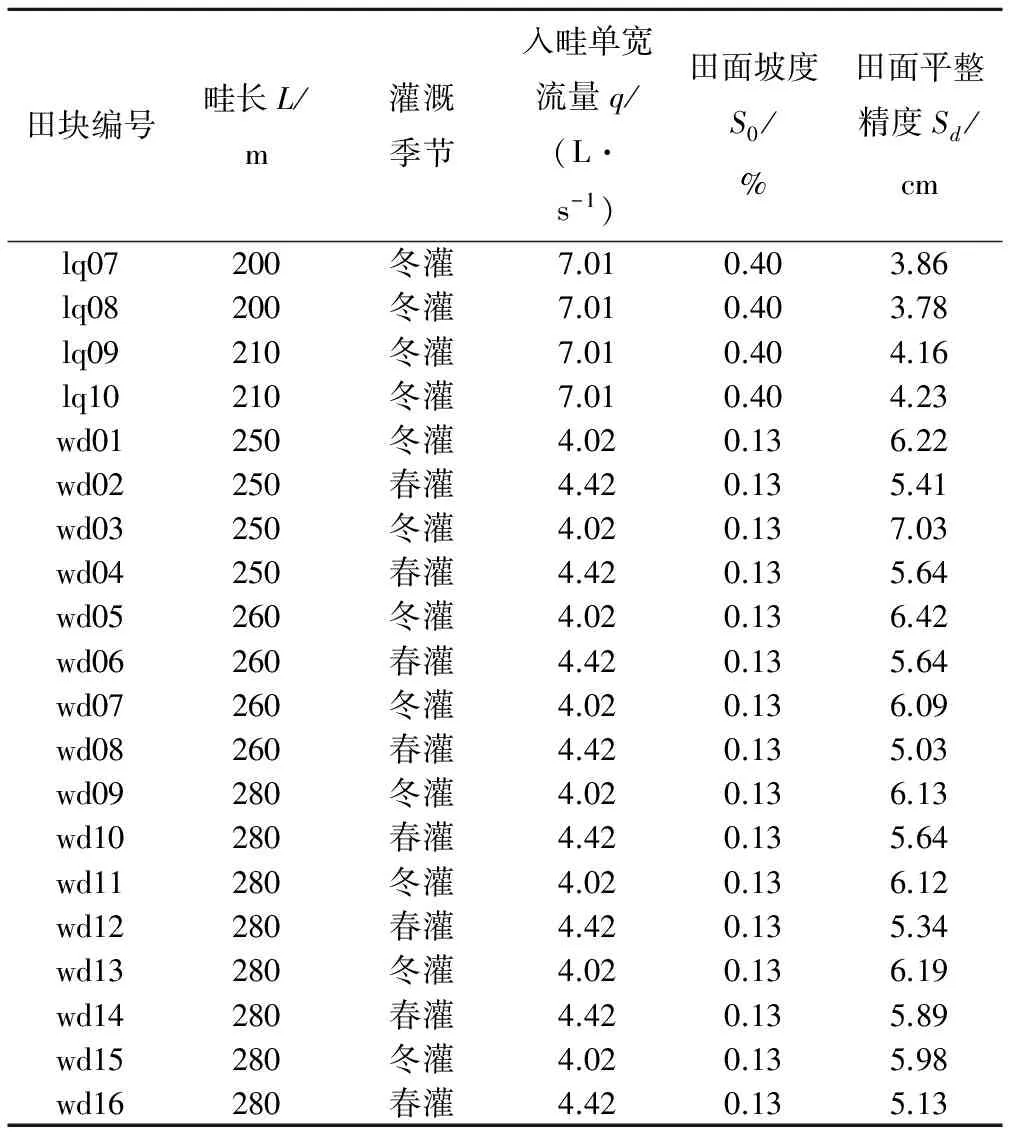
续表1 先验信息田块灌溉基本资料
1.3.2样本信息
取样本信息为来自新疆222兵团典型田块的20组灌溉资料,X=(X1,X2,…,X20),典型田块基本信息见表2。实测灌溉资料也包括田块规格、田面微地形、灌溉开始和关口时间、灌溉水流推进过程、入畦流量等,田面微地形和水流推进消退时间的测点间距为5 m。
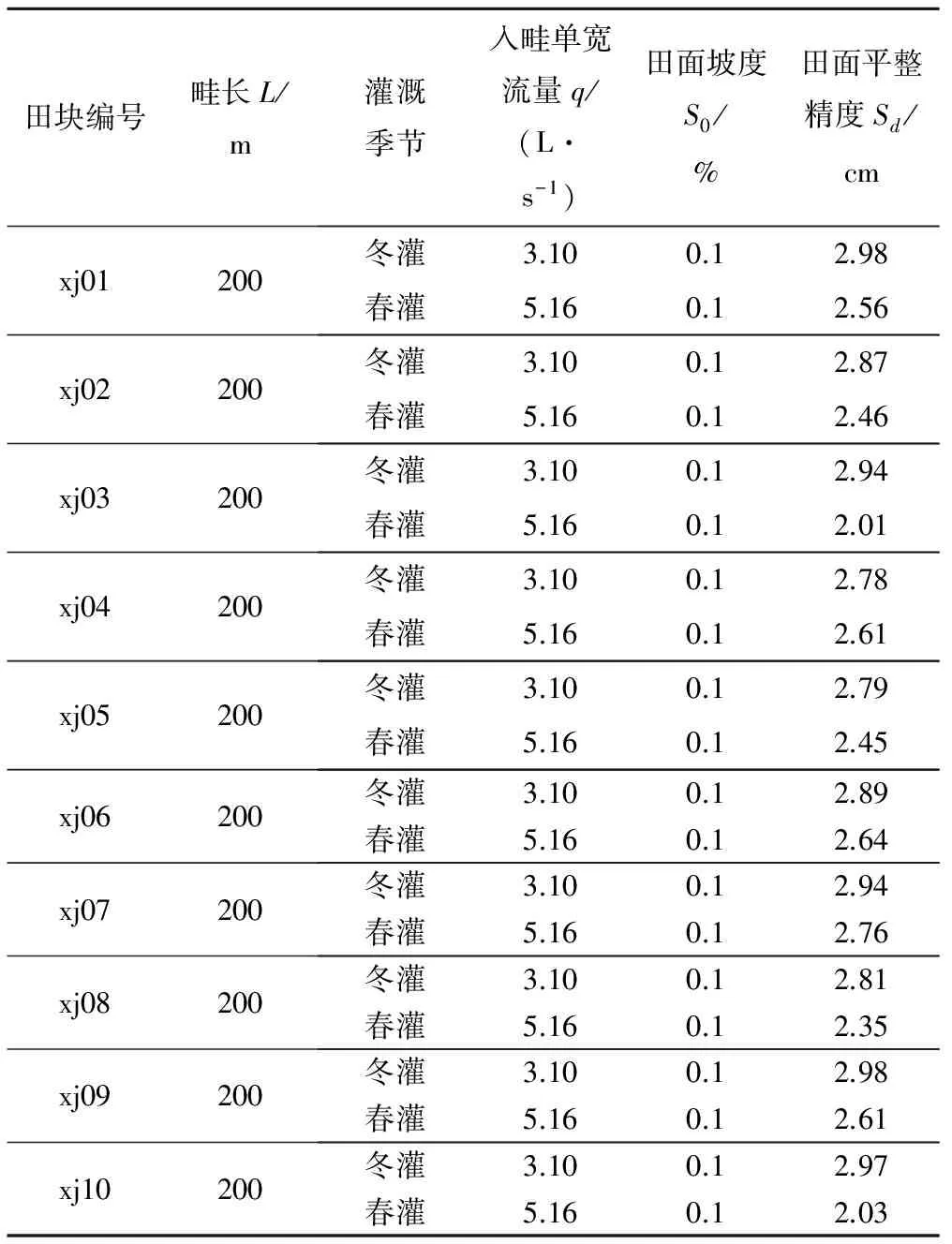
表2 样本信息田块灌溉基本资料
2 结果与分析
2.1 确定先验分布函数
因水流推进时间影响相对较大,选定灌溉水流推进过程模拟值与实测值之间的平均相对误差(AREadv)为随机变量。贝叶斯方法的一个主要问题是如何利用先验信息确定先验分布,因为先验分布有很大的主观性、随意性。采用常用的直方图法推断其先验分布,估计先验分布密度函数。
现以选取60%数据量为例,确定水流推进过程模拟值与实测值之间的平均相对误差的先验分布,并分析根据先验灌溉信息准确预测控制后验灌溉过程所需的合理数据量。对于50组先验数据,根据60%的实测水流推进数据采用反求法计算入渗参数k和a,并将得到的土壤入渗参数代入地面灌溉模拟模型(田面糙率系数取经验值:冬灌取0.08,春灌取0.1,且经过验证不同的经验取值对本文结论影响不大),对整个水流运动过程进行预测模拟,计算整个水流推进过程模拟值与实测值之间的平均相对误差。
采用基于混合数值解法的一维全水动力学畦灌模型对畦灌水流运动过程进行模拟,水流推进过程模拟值与实测值之间的平均相对误差如下(该误差值为连续型随机变量AREadv,则π(AREadv)为AREadv的先验分布,π(AREadv|x)为AREadv的后验分布)。
(4)
式中:t0i-adv是水流推进过程中点i处的实测值;tsi-adv是点i处的水流推进模拟值;n′为测点数。
计算出50组水流推进过程模拟值与实测值之间的平均相对误差最小值、最大值分别为2.18% 、27.46%,即所有数据落在区间[2.18,27.46]上,现取能覆盖区间[2.18,27.46]的区间[0,28],将区间[0,28]等分为7个小区间,小区间的长度记为Δ,Δ=(上限-下限)/7=4。数出落在每个小区间内的数据的频数fi,计算出频率fi/n(n=50,i=1,2,…,7)见表3。
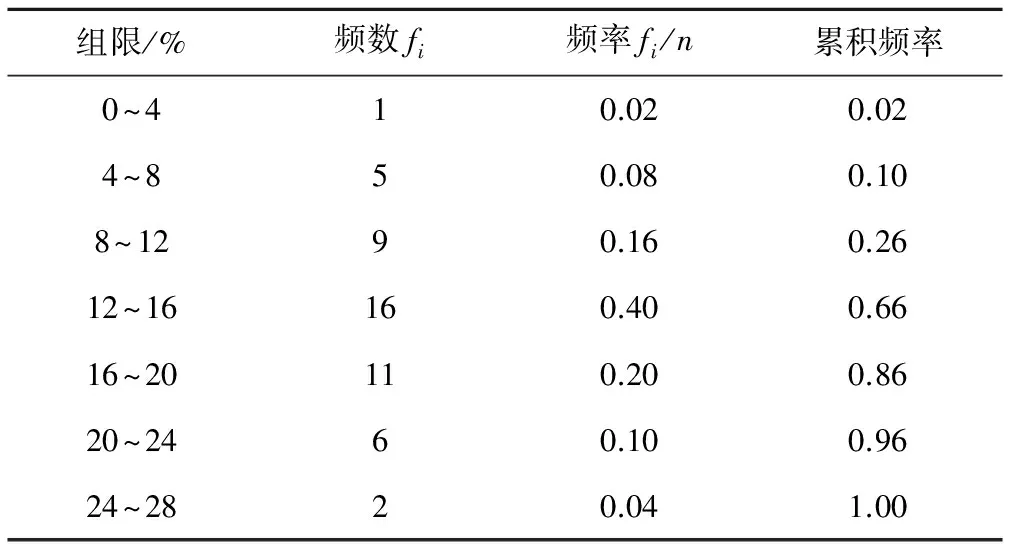
表3 平均相对误差频率计算
根据表3中数据自左向右依次在各个小区间上作以fi/n/Δ为高的小矩形,见直方图1。小矩形的面积就等于数据落在该小区间的频率fi/n。从图1中看出,直方图的外廓曲线中间高,两头低,有一个峰,类似正态分布曲线。
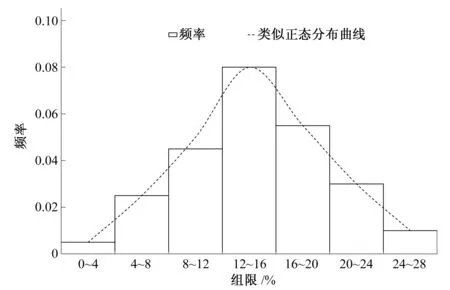
图1 先验分布频率直方图
为进一步确认先验分布是否服从正态分布,作χ2拟合检验如下。
H0:AREadv的概率密度为:
AREadv<+∞
(5)
由极大似然估计法得μ,τ2的估计值分别为14.7和5.02,在H0下将θ可能取值的区间(-∞,+∞)分为7个小区间,并取事件Ai(见表3中第1列所示)。若H0为真,则θ的概率密度函数的估计为:
(6)
按式(5)查正态分布的分布函数表可得概率P(Ai)的估计,计算见表4。

表4 检验计算
现χ2=52.33-50=2.33, 因为χ20.1(k-r-1)=χ20.1(7-2-1)=7.779>2.33,故在0.1水平下接受H0,由此可从理论上证明水流推进过程模拟值与实测值之间的平均相对误差的先验分布服从正态分布。正态分布(Normal distribution)又名高斯分布(Gaussian distribution),是一个在数学物理及工程领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。在自然现象和社会现象中,大量随机变量都服从或近似服从正态分布。
2.2 根据先验地表水流推进数据控制畦灌过程的适宜数据量
由水流推进过程模拟值与实测值之间的平均相对误差的先验分布π(AREadv)~N(14.7,52),结合样本信息推断后验分布π(AREadv|x)及置信区间。
(8)
由此可以获得θ的1-α置信区间。令:

同理,可以根据灌溉信息采集数据量为40%,50%,60%,70%,80%的计算数据,分析部分数据推求整个水流运动过程的模拟值与实测值的平均相对误差(AREadv)随灌溉信息采集数据量x的变化规律,作散点图并画出趋势线见图2。

图2 AREadv随灌溉信息采集数据量x的变化趋势散点与拟合曲线
由图2可知,AREadv随灌溉信息采集数据量x呈幂函数变化趋势,其幂指数为负数的减函数,拟合方程为:
AREadv(x)=0.041 8x-2.50≤AREadv≤1
(9)
由此可得,针对由先验灌溉信息准确预测控制后验灌溉过程所需的合理数据量研究,根据贝叶斯统计方法可论证出如下结论:对于一般的田块(即与本文试验田块的灌溉技术要素相近),当采用灌溉信息采集数据量分别为40%、50%、60%、70%和80%的实测水流推进数据时,水流推进过程模拟值与实测值之间的平均相对误差为40%、25%、15%、10%和7%,在精细地面灌溉智能控制技术实际应用中,可以根据需要的精度要求选择相应的灌溉信息数据量。
前人曾通过实测数据对灌水技术要素与灌溉信息数据量的影响进行研究,结果表明灌溉信息数据量受入畦单宽流量、田面纵坡、畦长等灌溉要素的影响,随入畦单宽流量、田面纵坡、畦长的增大而减小,随微地形的增大而增大(董孟军,2010年)。因此,对于灌水技术要素比较特殊的田块,需要根据实际情况选择适宜的灌溉信息数据量。
3 结 论
本文基于贝叶斯统计方法,根据先验信息、样本信息和似然函数,推导后验分布及置信区间,从理论上证明精细地面灌溉智能控制需采用的能够准确估算入渗参数并预测灌溉全过程的合理数据量。综合分析得出以下结论:
(1)采用60%的实测水流推进数据估算土壤入渗参数并预测灌溉全过程产生的平均相对误差落入[12.96,17.38]区间的概率为95%,即采用60%已经数据量推断未知灌溉过程是相对准确与合理的。
(2) 要使部分数据推求整个水流运动过程的模拟值与实测值的平均相对误差控制在40%、25%、15%、10%和7%左右,所需的合理数据量为40%、50%、60%、70%和80%。在精细地面灌溉智能控制技术实际应用中,可以根据需要的精度要求选择相应的灌溉信息数据量。本研究成果为精细地面灌溉智能控制系统中适用条件和合理数据量的确定提供了理论依据。
□
[1] 李益农. 我国地面灌溉技术评价及其发展趋势[C]∥ 中国水利学会首届青年科技论坛论文集. 北京:中国水利水电出版社,2004:201-207.
[2] Clemmens A J, Keats J B. Bayesian inference for feedback controlⅠ:theory[J]. Journal of Irrigation and Drainage Engineering,1992,118(3): 397-415.
[3] Clemmens A J, Keats J B. Bayesian inference for feedback control.Ⅱ:surface irrigation example[J]. Journal of Irrigation and Drainage Engineering,1992,18(3):416-432.
[4] Clemmens A J. Feedback control of basin irrigation system [J], Journal of Irrigation and Drainage Engineering, 1992,118(3):480-496.
[5] 董孟军. 基于推进距离的一维畦灌反馈控制方法研究[D].北京:中国水利水电科学研究院,2010.
[6] 白美健,李益农,许 迪,等. 精细地面灌溉实时反馈控制技术适应性分析[C]∥中国农业工程学会2014年学术年会论文集.
[7] 章少辉,许 迪,李益农. 基于混合数值解法的一维全水动力学畦灌模型[J]. 农业工程学报,2009,(9):7-14.
[8] 盛 骤,谢式千,潘承毅. 概率论与数理统计[M]. 北京:高等教育出版社,2001.
[9] 韦来生,张伟平. 贝叶斯分析[M]. 合肥:中国科学技术大学出版社,2013.
[10] 茆诗松,汤银才. 贝叶斯统计[M]. 北京:中国统计出版社,2012.
[11] Clemmens A J. Roughness or infiltration from surface irrigation advance [C]∥ ASCE. Proc. Irrigation and Drainage, 1990:46-53.
[12] Walker W R, Busman J D. Real-time estimation of furrow infiltration [J]. Journal of Irrigation and Drainage Engineering, 1990,116(3):299-318.
[13] Burt C M,Clemmens A J, Strelkoff T S, etal. Irrigation performance measure: efficiency and uniformity[J]. Journal of Irrigation and Drainage Engineering, 1997,123(6):423-442.
[14] Kanya L, Khatri, R J Smith. Toward a simple real-time control system for efficient management of furrow irrigation[J]. Journal of Irrigation and Drainage Engineering, 2007,56(4):463-475.
[15] R K Koech, R J Smith, M H Gillies. A real-time optimisation system for automation of furrow irrigation[J]. Journal of Irrigation and Science, 2014,32:319-327.
[16] 许 迪, 李益农. 精细地面灌溉技术体系及其研究的进展[J]. 水利学报, 2007,38(5):529-536.
[17] 白美健. 微地形和入渗空间变异及其对畦灌系统影响的二维模拟评价[D]. 北京:中国水利水电科学研究院,2007.
[18] 许 迪,蔡林根,茆 智,等. 引黄灌区节水决策技术应用研究[M]. 北京:中国农业出版社,2004.
[19] 章少辉. 土壤入渗参数和糙率系数的优化反求方法及应用[D]. 北京:中国水利水电科学研究院,2005.
[20] 王占军. 地面灌溉参数与灌水技术要素优化研究[D]. 西安:西安理工大学,2009.

