土壤水高矿化度对粉质黏土水力特性的影响

栗现文，周金龙，周念清，贾瑞亮

(1. 同济大学水利工程系，上海 200092；2. 新疆农业大学水利与土木工程学院，乌鲁木齐 830052)

0 引 言

在非饱和带水盐运移计算中，土壤水分特征曲线的测定及水力参数的获取是基础性工作，是研究土壤水分入渗、蒸发、土壤侵蚀及溶质运移过程的关键[1-3]。关于土壤水力特性的影响因素及参数拟合，国内外学者也开展了大量研究。刘建立等[4]将确定土壤水力性质的各种直接方法和间接方法(如土壤转换函数、分形方法、数值反演方法和经验公式法等)进行了系统总结。查元源等[5]提出了一种利用剖面土壤含水率推求土壤水力参数的方法。Thakur等[6]以粉土和高岭土为对象，在高吸力段干密度对土壤水分特征参数和土壤吸力影响较小。不同耕作和灌溉施肥方式也对土壤结构产生作用，进而影响土壤水力特性[7-9]。

在极端干旱潜水蒸发强烈区域，潜水埋深较浅，矿化度一般为3～10 g/L，局部为10～30 g/L，最大可达100 g/L以上，如在新疆内陆盆地中央冲积平原或湖积平原三角洲地带，地下水径流滞缓，潜水埋深浅且通过蒸发消耗，使得地下水中盐分积累，高矿化度潜水水化学类型为Cl·SO4型或Cl型[10]。高矿化度条件下的潜水蒸发规律[11-13]、毛细水上升高度[14]、土壤孔隙结构[15]等均与淡水条件下有显著差异，若将传统淡水条件下获取的土壤水力特征参数直接用于高矿化度潜水蒸发数值计算，其结果令人质疑，因此，探讨土壤水高矿化度对水力特性的影响具有重要意义。

本文通过实验获取不同土壤水矿化度处理(淡水、30、100及250 g/L)粉质黏土脱湿过程土壤水分特征曲线，利用RETC软件选取通用模型拟合各组曲线，进而分析比较不同矿化度处理下的土壤水力特征参数，为深入开展高矿化度潜水蒸发数值计算提供支持。

1 材料与方法

1.1 土壤水分特征曲线的测定

Cl-Na型水是干旱区较常见的高矿化度潜水水化学类型，试验设置4种矿化度的NaCl溶液与之对应，分别为淡水(1 g/L)、30、100、250 g/L。试验用土样取自新疆南部典型干旱区，风干磨细去杂后，过2 mm孔径标准筛，并通过比重计法测定土壤粒径组成(如表1)。将混合均匀的土样，按干容重1.755 g/cm3装填4组，以不同矿化度溶液对其作饱水处理。采用土壤水分特征曲线仪测定不同土壤水矿化度处理(以下简写为TDS-F、TDS-30、TDS-100和TDS-250)土样脱湿过程水分特征曲线，即测定土壤体积含水率及相对应土壤水吸力值(土壤负压绝对值)。

表1 试验土样颗粒分析组成Tab.1 Soil particles of the experiment

1.2 土壤水分特征曲线模型

由于尚不能根据土壤基本性质从理论上得出土壤水的基质势与含水率的关系，为了分析应用的方便，常用实测结果拟合出经验关系[16]。有多种经验函数模型用来描述土壤水分特征曲线[17-20]，在这些模型中，最为常用的是van Genuchten模型(简称VG模型)[18]：

(1)

式中：θs为土壤饱和体积含水率，cm3/cm3；θr为残余土壤体积含水率，cm3/cm3；h为土壤负压，cm；α、m、n为待定系数。

用经验公式估计土壤水力性质需要大量的土壤水分含量和与之对应的压力水头实测数据，然后通过非线性最小二乘法优化求得经验模型参数。美国国家盐改中心(US Salinity Laboratory)提供的RETC软件[21]，专门用于确定土壤水分特征曲线，包含了多种土壤水分模型(经验公式)用以拟合实测试验数据，以分析或预测非饱和土壤的水力性质，在选择水分特征曲线模型时，也要选择不同的求解K(土壤非饱和水力传导度)、D(扩散率)的Mualem或Burdine模型(本文中对模型采用组合写法，如van Genuchten-Mualem)。

2 结果分析

2.1 不同土壤水矿化度处理水分特征曲线

根据试验实测数据绘制不同土壤水矿化度处理水分特征曲线如图1所示。在监测过程中发现，同一含水率可对应一定取值范围的土壤水吸力，为比较不同处理间差异，此处取均值绘制各组土壤水分特征曲线。笔者曾对不同矿化度土壤水分特征曲线形态及孔隙结构影响进行过分析[15]，各处理水分曲线比水容量相近，但局部存在差异，表现为TDS-100及TDS-250处理对水分的吸持能力明显小于TDS-30及TDS-F处理。分析当量孔径变化可推知，TDS-30处理使土体中等孔隙体积变小；TDS-100处理使土体较小孔隙体积变小；TDS-250处理使土体较大孔隙体积变小。

注：θ1、θ2为土壤水分特征曲线上任意两点对应的含水率(θ1>θ2)，d1、d2为与之对应的土壤当量孔径。图1 不同矿化度土壤水分特征曲线[15]Fig.1 Soil water characteristics curves under different TDS treatments[15]

2.2 拟合模型

如前所述，RETC软件包含拟合土壤水分特征曲线的多种模型，通过对实测土壤水分特征曲线的拟合，可确定模型中包含的各项参数。但某种模型并非对所有的土壤水分特征曲线都适用，为比较4组不同土壤水矿化度处理对水分特征参数的影响，最好建立通用的同种拟合模型。通过建模试算发现，只有van Genuchten-Burdine模型可以同时拟合各处理土壤水分特征曲线，如图2所示。TDS-F、TDS-30、TDS-100和TDS-250处理拟合精度均较高，R2分别达到0.995 8、0.994 3、0.995 9和0.986 0。

值得注意的是，对于各组实测土壤水分特征曲线，土样开始脱水后，土壤水吸力与含水率间并不服从严格意义上的单调对应关系；尤其在土壤含水率较小时，每一含水率都对应一定的土壤水吸力变化区间，即只有当土壤水吸力增大到一定程度后，土壤含水率才发生变化而使水分特征曲线形态表现为阶梯状。因此，准确描述各组土壤水分特征曲线变化的拟合模型，严格意义上讲也应是多值函数的形式，对此需做更深入研究。

2.3 土壤水矿化度对水分特征参数的影响

基于上节拟合模型可识别出模型中各参数值(表2)，并可比较各处理对同一参数的差异性表现。不同处理拟合参数与RETC软件中的神经网络预测(NNP)结果对比均有明显差异。不同矿化度处理间差异表明，同一土质在不同土壤水矿化度作用下，对土壤水分特征参数产生明显影响。而神经网络预测结果与各处理间的差异性，推测为实际监测所得土壤水吸力与含水率间的多值对应关系，对曲线形态产生影响，进而造成RETC软件拟合失真所致。同一参数各处理间的差异性对比则相对表明矿化度对各土壤水力参数的影响。

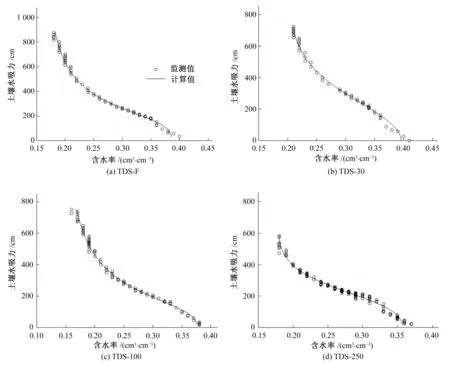
图2 不同土壤水矿化度处理水分特征曲线拟合效果Fig.2 Comparison of the measured and calculated of the soil water retention curves under different TDS treatments

处理TDSFTDS30TDS100TDS250NNP各处理差异θr0.15660.20110.13840.17730.0397TDS30>TDS250>TDSF>TDS100>NNPθs0.38600.39560.37650.35690.3134TDS30>TDSF>TDS100>TDS250>NNPθs*0.40000.41000.38440.3719-TDS30>TDSF>TDS100>TDS250α0.00430.00120.00510.00200.0247NNP>TDS100>TDSF>TDS250>TDS30n3.12632.00502.64642.57921.2882TDSF>TDS100>TDS250>TDS30>NNP

注：θs*为实测饱和体积含水率；NNP为RETC软件神经网络预测结果(Neural Network Prediction)；参数m一般可由n值计算推定，未在此列出。

TDS-30处理对应的残余体积含水率θr最大，是其持水能力较强的体现。各处理残余体积含水率拟合值均相对较大，是因试验较难测得完全脱水状态的土壤水分特征曲线，而后期阶梯状的含水率与土壤水吸力间的多值对应关系使van Genuchten-Burdine模型产生拟合失真。模型拟合结果对应的饱和含水率θs均小于实测值，其在接近饱和含水率处的拟合效果相对较差；各土壤水矿化度处理饱和含水率θs接近，总体上表现为土壤水矿化度越大饱和含水率越小。TDS-30>TDS-F处理可能为测量误差所致，因从理论上讲，矿化度越大，土壤完全失水后，盐分所占空间越大，总的孔隙体积则相对变小，因此饱和含水率也相应较小。由VG模型表达式可知，α、n值对拟合模型曲线形态有重要影响，相比其他土壤水矿化度处理，TDS-30处理对应的α、n值均最小。各矿化度处理水分特征曲线拟合模型具体形式为：

TDS-F处理：

(2)

TDS-30处理：

(3)

TDS-100处理：

(4)

TDS-250处理：

(5)

非饱和水力传导度K是描述土壤水力特性的一个重要参数[22]，是土壤含水率或负压的非线性函数。RETC软件拟合的不同土壤水矿化度处理非饱和水力传导度随含水率变化如图3所示。各处理均表现为随含水率减小K值迅速衰减，TDS-30处理衰减最快，TDS-100处理衰减速率大于TDS-F处理。体积含水率小于0.23时，各处理K值差异不明显；而当体积含水率介于0.23～0.36(TDS-250处理饱和含水率)时，同一含水率对应的K值表现为TDS-250>TDS-F>TDS-100>TDS-30。土壤孔隙分布对K有重要影响，笔者前期研究表明，在此粉质黏土条件下，随着土壤水分散失，盐分积累，TDS-30处理使土体中等孔隙体积变为小孔隙[15]，进而影响K值。由此推知，中等大小孔隙的变化对该岩性土壤非饱和水力传导度影响较为显著。

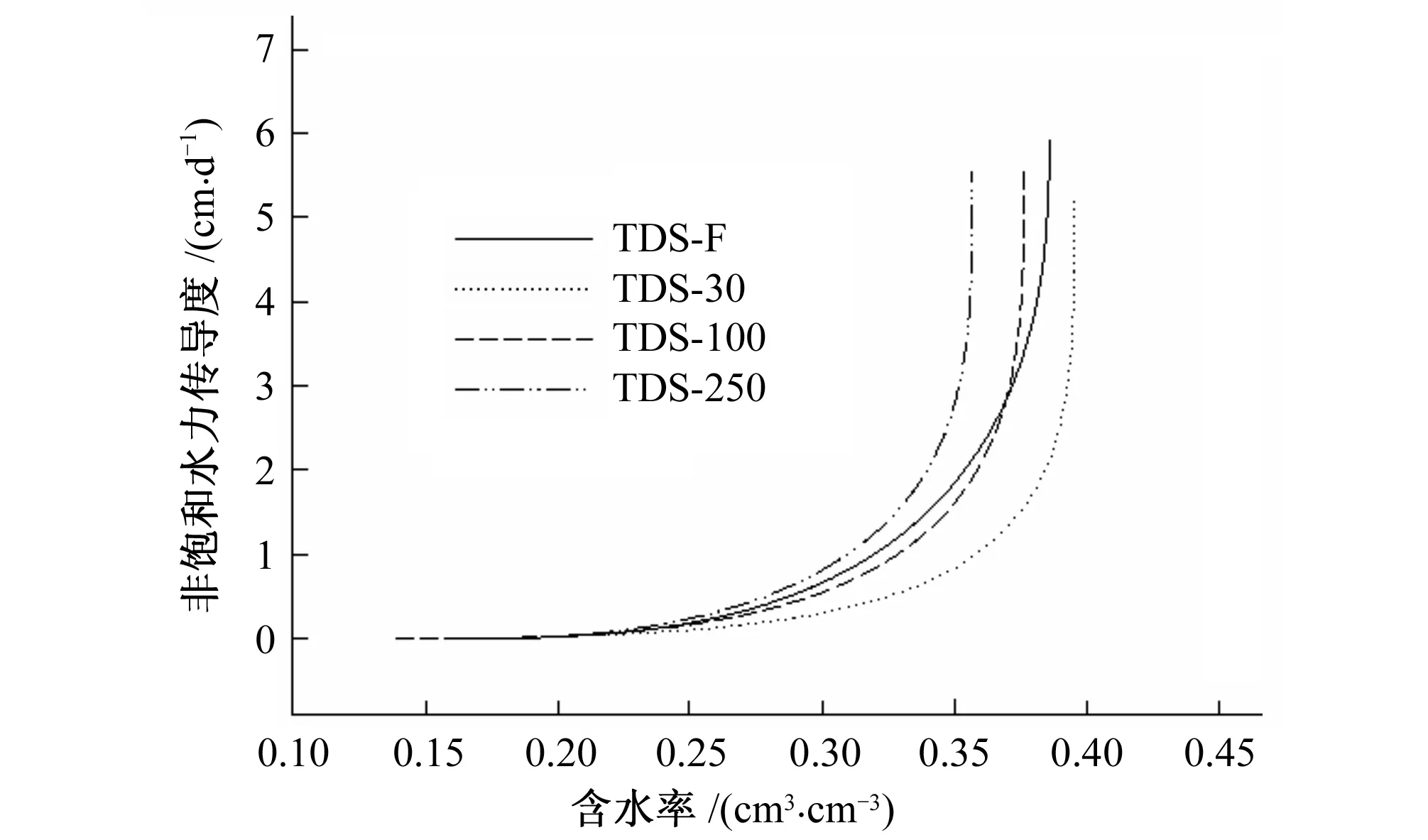
图3 不同矿化度处理水力传导度随含水率变化Fig.3 Hydraulic conductivity of different TDS treatments with the variation of water content

3 结 语

(1)Van Genuchten-Burdine模型是拟合淡水及30、100 、250 g/L土壤水矿化度处理水分特征曲线的通用模型，R2分别达到0.9958，0.994 3，0.995 9和0.986 0，拟合精度较高。

(2)不同矿化度处理脱湿过程土壤水分特征曲线形态显示，土样开始脱水后，土壤水吸力与土壤含水率间并不服从严格意义上的单调对应关系。在吸力较大阶段，当土壤水吸力增大到一定程度时土壤含水率才发生变化，曲线形态呈阶梯状。

(3)粉质黏土条件下，土壤水矿化度对水分特征参数产生明显作用，TDS-30处理对应的残余体积含水率θr最大，α、n值最小；其他处理总体上表现为矿化度越大饱和含水率θs越小。

(4)TDS-30处理对应的非饱和水力传导度K衰减最快。体积含水率介于0.23～0.36(TDS-250处理饱和含水率)时，各处理K值表现为TDS-250>TDS-F> TDS-100>TDS-30；中等大小孔隙的变化对粉质黏土非饱和水力传导度影响较为显著。

[1] 程冬兵，蔡崇法. 室内基于土壤水分再分布过程推求紫色土导水参数[J]. 农业工程学报, 2008,24(7):7-12.

[2] Hwang S I, Powers S E. Estimating unique soil hydraulic parameters for sandy media from multi-step outflow experiments[J]. Advances in water resources, 2003,26(4):445-456.

[3] 邵明安，王全九，黄明斌. 土壤物理学[M]. 北京: 高等教育出版社, 2006.

[4] 徐绍辉，刘建立. 土壤水力性质确定方法研究进展[J]. 水科学进展, 2003,14(4):394-401.

[5] 查元源，周发超，杨金忠. 一种由土壤剖面含水率估算土壤水力参数的方法[J]. 水利学报, 2011,42(8):883-891.

[6] Thakur V K S, Sreedeep S, Singh D N. Parameters affecting soil-water characteristic curves of fine-grained soils[J]. Journal of Geotechnical and Geoenvironmental Engineering. 2005,131(4):521-524.

[7] 王志超，李仙岳，史海滨，等. 农膜残留对土壤水动力参数及土壤结构的影响[J]. 农业机械学报, 2015,46(5):101-106.

[8] Naveed M, Moldrup P, Vogel H, et al. Impact of long-term fertilization practice on soil structure evolution [J]. Geoderma. 2014, 217-218:181-189.

[9] Blanco-Canqui H, Lal R. Impacts of long-term wheat straw management on soil hydraulic properties under no-tillage[J]. Soil Science Society of America Journal, 2007,71(4):1 166-1 173.

[10] 栗现文，周金龙. 高盐度潜水蒸发试验研究现状及展望[J]. 地下水, 2011,33(2):11-14.

[11] 贾瑞亮，周金龙，高业新，等. 干旱区高盐度潜水蒸发溶解性总固体折算系数分析[J]. 水文地质工程地质, 2015,42(3):19-26.

[12] 贾瑞亮，周金龙，高业新，等. 干旱区高盐度潜水蒸发规律初步分析[J]. 水科学进展, 2015,26(1):44-50.

[13] 栗现文，周金龙，靳孟贵，等. 干旱区高盐度潜水蒸发试验研究[J]. 水资源与水工程学报, 2012,23(5):6-10.

[14] 栗现文，周金龙，赵玉杰，等. 高矿化度对砂性土毛细水上升影响[J]. 农业工程学报, 2011,27(8):84-89.

[15] 栗现文，周金龙，靳孟贵，等. 高矿化度土壤水分特征曲线及拟合模型适宜性[J]. 农业工程学报, 2012,28(13):135-141.

[16] 杨诗秀，雷志栋. 田间土壤水分通量确定方法的研究[J]. 水利学报, 1993,(7):1-9.

[17] Durner W. Hydraulic conductivity estimation for soils with heterogeneous pore structure[J]. Water Resources Research, 1994,30(2):211-223.

[18] Van Genuchten M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal. 1980,44(5):892-898.

[19] Kosugi K. lognormal distribution model for unsaturated soil hydraulic properties[J]. Water Resources Research, 1996,32(9):2 697-2 703.

[20] Brooks R H, Corey A H. Hydraulic properties of porous media[R]. Fort Collins: Colorado State University, 1964.

[21] Yates S R, Van Genuchten M T, Leij F J, et al. Analysis of measured, predicted, and estimated hydraulic conductivity using the RETC computer program [J]. Soil Science Society of America Journal, 1992,56(2):347-354.

[22] 王 康，张仁铎，王富庆. 基于连续分形理论的土壤非饱和水力传导度的研究[J]. 水科学进展, 2004,15(2):206-210.