工业流体系统风介质水力、热力耦合特性研究

赵 鑫 李琦芬 上海电力学院能源与机械工程学院陈 池 唐永东 上海宝钢节能技术有限公司

工业流体系统风介质水力、热力耦合特性研究

赵 鑫 李琦芬 上海电力学院能源与机械工程学院
陈 池 唐永东 上海宝钢节能技术有限公司

利用连续性方程、动量方程和状态方程建立了稳定流动时管道压降的计算模型，并简化求解得出了压降计算公式，建立了热交换器水力模型，同时通过给出等效长度的计算方法使得其阻力计算与管道一致，进而将其加入管网水力计算，建立了管网各组件热力计算的数学模型；同时给出管网水力计算、节点温度计算及节点压力计算的数学解法，通过反复迭代校正管段流量、管段平均密度和定压比热的方式使得水力和热力计算耦合，并以实际管网为例，对管网水力、热力工况进行了计算，计算结果与实际运行结果比较表明，该方法可用于指导工程实践，将有助于提升流体系统的设计精度与节能挖掘深度。

工业流体系统；水力计算；热力计算；耦合特性

Fund Item: Shanghai Municipal Science and Technology Commission Plan Project （13dz1201700）

由流体机械组成的系统称为流体系统，工业流体系统遍及电力、冶金、石化、钢铁等各个行业，其运行的质量直接关系到生产装置和设备安全，关系到产品的产率和质量。工业流体系统是决定企业产能是否实现长期稳定的重要因素，是工业流程中重要的流程。由于流体机械量大面广，其电能的消耗量十分巨大，其中较大的三类为水泵、风机和压缩机。据中国流体工程学会的调查，在20世纪80年代初，仅水泵、风机和压缩机等三类流体机械，其年用电量可达全国年电力消费的40%以上，其中水泵占21%，全国拥有量达1 300万台以上；风机占10%，全国拥有量达230万台以上[1]。深入挖掘工业流体系统的节能潜力中，精准的工业流体系统能耗分析研究是关键问题，水力计算和热力计算的耦合研究是深入挖掘流体系统节能潜力的的基础问题。

在对流体管网作热力特性分析时，重点研究的流体介质应为气相流体（风），此时管网水力和热力工况是通过密度、定压比热等状态参数相互影响的。精确的耦合方法将有助于提升系统的流体系统设计精度与节能挖掘深度。

本文将求解管道的压降方程，并通过求解热交换器的等效长度，使得热交换器的阻力计算方法与管道一致，进而将其加入管网模型中参与水力计算；建立管网各组件热力计算的数学模型，提出管网水力、热力计算的数学解法，通过管网水力计算、节点温度计算、节点压力计算3个模块将水力计算和热力计算耦合起来，实现了水力和热力计算的同步进行，并对计算方法进行了实例验证。

1管网各组件水力计算数学模型

1.1 稳定流动时管道压降的计算模型

取管道中的一个微小流体段为控制体[2]，运用动量守恒定律、质量守恒定律以及能量守恒定律对其进行分析后可推导出流体稳定流动的数学模型，去掉模型中各能量项后可得管网水力计算数学模型，如下：

式中：x——管内轴向长度，m；

θ——管道与水平方向的夹角；

λ——摩阻系数。

为了对式（1）用解析法进行求解，必须将其简化，如下[3]：

（1） 在动量方程中，左边第一项为对流项，第三项为重力项。对流项只有在流速极大（接近声速）时才有意义，而无论流体管网中的介质是水还是蒸汽、空气，在管道中的流速都远远小于声速，故可以忽略对流项。

（2）考虑到管网中管段两端的高程差一般较小，故略去重力项。

模型简化如下：

由连续方程可推知：

将式（3）代入到式（2）中的第一式，可得：

考虑λ和T均为常数，当p从p1变化到p2、x1从0变化到L时积分可得：

式（5）即为忽略温度和密度变化时流体管道进行水力计算的基本公式。

无论流体管网中介质是气态还是液态，两者的摩擦阻力系数在本质上没有区别[4]。它的数值与其流动状态、管道内壁的粗糙度、连接方法、安装质量以及介质的性质有关，可依据流体力学相关手册得到。

1.2 热交换器的水力模型

由于间壁式热交换器的生产经验、分析研究和计算方法比较丰富和完整，所以在工程上使用较多。本节针对其中的板式热交换器建立水力模型。

无相变换热时板式热交换器的压力降可由下式推导计算得到[5]：

式中的系数b和指数d随板式热交换器的具体结构而定，指数d应为负值。

由于Eu=∆p /( ρω2)，可求得多程时压降为：

式中，m为流程数；v为工质在流道中的流速，m/s。

对于本文后续水力、热力耦合计算实例中所采用的BR0.23型板式换热器，其中压降—速度的曲线，如图1所示：

图1 BR0.23型板式换热器的压降—速度曲线

1.3 热交换器等效长度的计算

根据公式计算出热交换器的流动阻力后，进而可以将热交换器等效为长度为l的管道，参与水力计算。

将沿程阻力计算式写成以压降形式表现的等效长度方程，可得热交换管道等效长度l的计算式：

计算得出热交换器的等效长度后，记为管段的长度，则热交换器阻力的计算与管段一致，这样就把热交换器加入到管网模型中。

2 管网各组件热力计算的数学模型

2.1 管道的热力模型

（1）管道散热损失的计算[6,7]

式中

Qj——管段j沿途散热损失，kJ；

qjl——管段j单位长度热损，W/m；

Lj——管段j的长度，m；

1）管道架空或管沟敷设

此时可近似看作单层圆筒壁。圆筒壁的导热系数λ为常数，同时已知r=r1，一侧流体的温度为tf1，对流换热系数的表面传热系数为hl；r=r2一侧流体的温度为tf2，表面传热系数为h2，稳态传热过程中，。

单位管长的热流量可用传热系数k来表示：

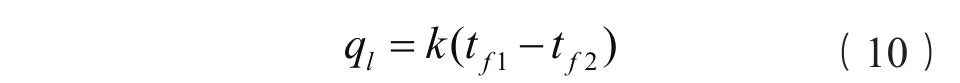
2）管道直埋敷设

此时管道内表面为第三类边界条件，而管道外表面则为第一类边界条件，即管道埋设土壤温度tw4已知，据此有直埋敷设的管道单位长度热损失计算公式：

（2）总传热系数的计算

实际的气体管道是由n层不同材料叠在一起组成的，由串联热阻叠加原则可知多层圆筒壁的总热阻等于各层热阻之和。传热系数的表达式如下：

式中：h1——流体对工作钢管内壁的换热系数，W/(㎡·k)；

λi——管道各层材料的导热系数，可由相应管道手册查得，W/(m·k)；

di——管道各层材料到管道中心的距离，m；

α——管道对土壤的换热系数（直埋）；管道与空气间的对流换热系数（架空或管沟），可由相应技术手册查得，W/(㎡·k)。

（3）管段温度降方程

管段温度降方程

式中：Δtj——管段 j 的温度降，℃；

Qj——管段j的有效热量损失，kJ；

Cpj——管段j内流体的平均定压比热，Cpj= ( Cpm+ Cpn)/ 2 ， kJ/( kg/K)，其中m，n为j=管段起点、终点号；

Gj——j管段的管段流量，kg/s。

tjm——管段j起点温度，K；

tjn——管段j终点温度，K。

2.2 热交换器热力模型

热计算是热交换器模拟运行的基础，传热方程式和平均温差公式参见文献[5]。

不同热交换器的传热系数不同，可以通过查对应的表取值。对于本文后续水力、热力耦合计算实例中所使用的BR0.23型板式换热器，厂家在其产品说明书中给出了传热系数—速度的曲线图，如图2。

3 管网水力、热力计算的数学解法

3.1 管网水力计算解法

运用管网水力计算基本方程进行水力计算的方法有解节点方程法、解环方程法、解管段方程法、梯度算法等。在众多的水力算法中，梯度算法有着显著的优点，例如方程结构可以使用紧凑稳定的稀疏矩阵解法，不需要处理初始流量分配以及多水源管网的管段共环等问题，可解环状管网和树状管网等。而线性化梯度算法，是在梯度算法的基础上，根据牛顿——拉夫森方法把管段水头损失方程线性化，推导出节点水头迭代方程和管段流量迭代方程。这种算法不但具有梯度法的优点，还能把管网管件如水泵、阀门等属性方程引入管网模型，简化了基本方程组，且计算收敛快、不发散。

对于一个含有p个未知流量G的管段，m个未知水头 的节点， 个已知水头或者固定水头节点，每个未知水头节点的需水量为的管网而言，由线性化梯度算法推导出的节点水头迭代方程和管段流量迭代方程如下所示[8]：

式中A1=(aij)m×p，当管段j流入节点i时为-1，当管段j流出节点i时为+1，当管段j不与节点i连接时为0；A2=(afj)NF×p，当管段j流入节点f时为-1，当管段j流出节点f时为+1，当管段j不与节点f连接时为0；固定节点水头值组成的矩阵为；M是由riGi组成的斜对角p阶矩阵， 为综合阻力系数。

图2 BR0.23型板式换热器的传热系数—速度曲线

3.2 节点温度计算解法

节点温度计算中，满足三个方程组：节点流量连续性方程组 AGj+ G0= 0；管段温度降方程组 ATT=∆ t；以温降形式表现的管段流量方程组Ct*∆ t= G。由以上三式可得求解节点温度的方程组：

式中，G0是指节点输入或输出的流量矩阵，为m×1阶矩阵，当节点无输入或输出的流量时，此项为0，单位m³/s。

Ct*是对节点温度方程组（14）进行线性化处理时的线性化因子，为节点对角p×p阶矩阵，其计算式如下：

其中， Cpj——管段j内流体的定压比热，Cpj= ( Cpm+ Cpn)/ 2 ，其中m，n为j管段起点、终点号，kJ/( kg·K)；

Gj——j管段的管段流量，各管段流量可在水力计算平衡后得到，kg/s；

Qj——管段j的有效热量损失，对管网系统而言，吸收热量时为负，释放热量时为正，各管段有效热量损失的计算依赖管网各组件热力计算数学模型的建立，kJ。

方程组（17）中仅有温度向量T未知，给定温度边界条件后可通过迭代求解得到管网中各节点温度。

3.3 节点压力计算解法

节点压力计算中，满足：节点流量连续性方程组 AG+ G = 0；管段压力降方程组 ATp=∆ p；j0以压降形式表现的管段流量方程组。由以上三式可得求解节点压力的方程组：

Cp*是对节点压力方程组（5）进行线性化处理时的线性化因子，为节点对角p×p阶矩阵，其计算式如下：

其中，Dj——管段j的内径，m；

λj——管段j摩阻系数；

Gj——j管段的管段流量，各管段流量可在水力计算平衡后得到，kg/s；

Lj——管段j的长度，m。

方程组（19）中仅有压力向量p未知，给定压力边界条件后可通过迭代求解得到管网中各节点压力。

4 管网水力、热力特性耦合计算方案

水力和热力耦合计算是通过对管段密度ρj、动力粘度μj、定压比热Cpj反复迭代来实现的。具体方法是以汽源点的温度、压力为初始值，初始各管段流速可任意假设，根据温度和压力求得各节点密度ρi，动力粘度μi，定压比热值Cpi，各管段的密度ρj、动力粘度μj、定压比热Cpj，取管段前后节点的平均值。得到管段的物性参数后，计算各管段雷诺数Rej以及对应的阻力系数λj，然后计算水力迭代矩阵M及热力线性化因子Ctj*，进而通过水力迭代公式和热力迭代公式得到各管段流量Gj(1)，各节点压力Pi(1)和温度Ti(1)。当前后两次管段流量的差值和前后两次节点温度的差值不满足允许精度时，令Gj(0)= Gj(1)，Ti(0)= Ti(1)，Pi(0)= Pi(1)进行迭代计算，直到满足精度要求为止。

管网水力 、热力耦合计算流程如图3所示。

5 实例验证

以上海市某电厂锅炉的入炉风系统为例，进行管网水力、热力耦合计算。简化后的锅炉入炉风系统管网图如图7所示，该管网中有1台风机，1个热交换器，2条管道，其中风机选用山东淄博冠博风机有限公司生产的GY4-68型锅炉离心通风机，其处理风量为22 000 m³/h时，全压为2 000 Pa；热交换器采用山东淄博泰勒换热设备股份有限公司生产的BR0.23型板式换热器，其额定换热量为2 000 kJ；管道P1长度20 m，直径500 mm，管道P3长度15 m，直径500 mm，节点2、3的需气量为0，节点1、4的需气量分别为-6 100 L/s 和6 100 L/s，风机出口端气体温度T1=20℃。

图3 管网水力、热力耦合计算流程

管网水力、热力耦合计算分为以下水力计算、温度计算、压力计算三个模块。水力计算模块中，根据线性化梯度算法进行迭代计算，其中精度eps1取0.1，第一次试算时的管段流速为1 m/s，当绝对流量变化之和相对于所有管段的总流量的绝对值小于0.1时水力计算结束，得到各管段流量和流速。温度计算模块中，管道单位长度换热量qjl采用工程算法，根据《城市供热工程》中表格取管道最大允许热损失为50 W/㎡，各节点温度在第一次试算时取20℃，节点温度差的容许精度eps2取0.1，满足条件时的各节点温度值为T1(1)=20℃，T2( 1 )= 1 9 . 7 4 ℃，T3(1)=373.49℃，T4(1)= 343.30℃。压力计算模块中，以温度计算最后得到的各节点温度Ti(1)及压力边界条件为准，本实例中p10= p20= p30= p40=103 325 Pa，节点压力差的容许精度eps3取0.1，满足条件时的各节点压力值为p1(1)=103 325 Pa，p2(1)=78 465.79 Pa，p3(1)=42 559.28 Pa，p4(1)=23 952.68 Pa。

将管网水力、热力耦合计算得到的结果与单纯水力计算得到的结果以及运行数据进行比较，水力、热力耦合计算、单纯水力计算以及运行工况下各节点压力值如表1所示。

图4 简化后得到的系统管网图

表1 各节点压力值对比

图5 节点压力对比曲线

由表1以及图5可以看出，本实例水力、热力耦合计算时节点压力的相对误差最大为7.35%，最大相对误差处，节点压力的绝对偏差为1 899.32 Pa，综合分析时认为管网水力、热力耦合计算结果满足工程精度要求，而采用单纯水力计算的结果与实际运行数据相比较，误差较大。

管网水力、热力耦合计算比单纯的水力计算的结果更符合管网实际运行数据，从而标明对工作介质为气相流体的流体系统进行分析计算时考虑温度对工作介质的影响是非常重要的。

6 结语

1）从合理分析流体系统设备动力与阻力特性的角度出发，建立了管道和热交换器的水力计算数学模型，给出了求解管段的压降计算公式，以及热交换器的等效长度的计算方法，使得热交换器的阻力计算与管段计算方法一致；

2）从管道的传热特性出发，建立了流体介质为气相流体时管道的热力计算数学模型，对管道进行了较为准确的热力计算，同时通过热交换器对数平均温差、整体的热交换系数及热交换面积的计算，建立了其传热方程式；

3）建立了管网水力、热力计算的数学解法，通过水力计算、节点温度计算和压力计算三个模块，实现了管网水力、热力特性的耦合计算，同时对上海市某电厂的入炉风系统进行计算，将耦合计算得到的结果与单纯水力计算得到的结果以及运行数据进行对比分析，耦合计算时节点压力的相对误差最大为7.35%，最大相对误差处，节点压力的绝对偏差为1 899.32Pa，综合分析时认为管网水力、热力耦合计算结果满足工程精度要求，而采用单纯水力计算的结果与实际运行数据相比较，误差较大，标明该耦合计算模型可用于指导实际工程的设计及运行调节计算。

本文的工作是工业流体系统水力、热力耦合计算的核心算法研究，精确的耦合方法将有助于提升系统的流体系统设计精度与节能挖掘深度。

[1] 渠时远.流体机械节能减排现状、任务和对策[J].通用机械,2012,(10):34~36

[2] 周游.天然气长输管线末段与城市高压外环不稳定流动及末段储气的研究[D].济南: 山东建筑工程学院硕士学位论文,2004

[3] 哈尔滨建筑工程学院,北京建筑工程学院,同济大学等.燃气输配(第二版)[M].北京：中国建筑工业出版社,1995,92~96

[4] 付祥钊,王岳人.流体输配管网[M].北京:中国建筑工业出版社,2001,112~115

[5] 史美中,王中铮编.热交换器原理与设计[M].南京:东南大学出版社,2009,112~115

[6] 张增刚.蒸汽管网水力热力耦合计算理论及应用研究[D].北京:中国石油大学博士学位论文,2008

[7] 李国俊.宝钢蒸汽系统运行参数优化研究[D].上海:上海理工大学硕士学位论文,2008

[8] Lewis A. Rsssman. Epanet2 Users Manual[M]. Supply and Water Resources Division National Risk Management Research Laboratory.2000

Research on Wind Medium Hydraulic and Thermal Coupling Characteristics in Industrial Fluid System

Zhao Xin, Li Qifeng
Shanghai Electric Power University
Energy and Mechanical Engineering College
Chen Chi, Tang Yongdong
Shanghai BaoSteel Energy Saving Technology Co.,Ltd

The article uses continuous equation, momentum equation and state equation to establish steady flow pipeline pressure drop calculation model and obtains simplified calculation formula of pressure drop, builds up hydraulic model of heat exchanger, meanwhile it shows resistance calculation is consistent with pipeline calculation through providing calculation method of equivalent length, which is integrated into hydraulic calculation of pipe network to establish of thermodynamic calculation mathematical model for each component of pipe network. It also puts forward mathematical solution of pipe network hydraulic calculation, node temperature calculation and node pressure calculation. Through repeated iteration to correct flow rate, average density and specific heat constant pressure method, it finishes coupling of hydraulic and thermal calculation. Based on the existing example, the author conducts calculation of pipe network hydraulic and thermal conditions and the comparison of the calculated results with the practical operation shows that this method can be used to guide the engineering practice, which will help improve fluid system design accuracy and energy conservation depth.

Industrial Fluid System, Hydraulic Calculation, Thermal Calculation, Coupling Characteristics

上海市科委科研计划项目（13dz1201700）

10.13770/j.cnki.issn2095-705x.2016.01.006