泗水县农业水资源高效利用分析
周振民,刘兆旋(华北水利水电大学,郑州 450011)
1 研究区概况
山东省泗水县位于山东省中南部泰沂山区南麓,系泰沂蒙余脉低山丘陵区,多年平均径流深在240.9~263.1 mm,降水保证率50%时径流深203~230.2 mm;降水保证率75%时径流深117.0~145.7 mm。泗水县总面积11.18万hm2,其中耕地面积5.58万hm2,占总土地面积的49.89%,粮食作物主要有冬小麦、夏玉米等,经济作物主要有花生、蔬菜、瓜类等。现状年全县耕地控制灌溉面积2.15万hm2;有效灌溉面积1.89万hm2,复种指数为1.86。现状年灌溉水利用系数为0.50左右,规划到2020年项目区内的节水灌溉工程全部完成,农业灌溉水利用系数将获得极大提高。
2 柯布-道格拉斯生产函数及非充分灌溉理论
2.1 柯布-道格拉斯生产函数模型
柯布-道格拉斯生产函数(Cobb-Douglas Production Function)是用来求解一定社会生产力发展水平下劳动力、资金、物质等生产要素投入和产出的关系的数学函数,在经济学上使用非常广泛,通常简称为C-D生产函数[1]。最常用的柯布-道格拉斯生产函数是荷兰经济学者丁伯根改进的函数形式,其表现形式为:
Yt=AtKαLβ
(1)
式中:Yt是指特定时期的社会生产力发展水平;At是指特定时期研究领域相关技术发展水平;K是指在相应的社会生产力发展水平及技术水平下的资金投入量;L是指在相应的社会生产力发展水平及技术水平下劳动力投入量;α、β分别为资金和劳动力投入量对社会生产力发展水平提高的影响程度[2]。
国内学者晏庆国对丁伯根改进的函数做了进一步的论述:比较常用的改进的柯布-道格拉斯生产函数的表现形式为:
Y=AtKαLβ
(2)
式中:Y表示产出量;K表示资金的投入;L表示劳动的投入;At表示技术水平;α、β分别为资金、劳动投入的产出弹性[3]。
若对柯布-道格拉斯生产函数两边取对数,可以得到lnY=lnA+αlnK+βlnL。这样将上述的柯布道格拉斯生产函数转化成一个普通的多元线性回归模型,并建立回归方程对其进行回归分析。
在建立的回归方程中,α、β的大小分别决定了资金和劳动投入对产出量的影响程度,α、β值越大,产出量受其对应的投入要素的影响程度越大,反之,产出量受其对应的投入要素的影响程度越小。
2.2 非充分灌溉理论
非充分灌溉不同于传统的节水灌溉,它是在农业灌溉用水量不足的情况下,通过实验研究建立作物灌水量与作物产量之间的函数关系,实现有限水量最优分配[4]。非充分灌溉允许作物产量有一定程度的减少,在农业灌溉可用水量无法满足农作物整个生育期的需水量的情况下,以单方水产生的经济效益最大或单方水产出产量最大为目标,以农作物自身具有一系列对水分亏缺的自适应机制和有限缺水效应为基本理论,实行作物某个生育阶段缺水灌溉处理[5]。非充分灌溉理论的发展整体上可以概括为以下两个阶段:
(1)定性的概念阶段。通过研究农作物不同生育期对水量的敏感程度,制定一定的灌溉制度,在作物敏感程度较大阶段进行充分灌溉,减少敏感程度较低阶段的灌水量。本阶段并无法明确在不同阶段如何控制灌水量。
(2)定量的研究阶段。根据研究区气象、土壤、农业技术措等基本条件,充分研究有效灌溉水量与作物产量之间的关系,建立灌溉水量与作物产量函数关系式,根据实际降水、土壤含水率等情况对有限的水资源在农作物不同生育期进行定量分配,实现农作物灌溉“以产定水”。
3 研究区水资源供需平衡分析
3.1 水资源总量及可供水量预测分析
水资源量是指境内地表产流量及境外地表入流量与降水入渗地下水补给量之和,计算方式为地表、地下水资源量总和减去二者重复计算的河川基流量。泗水县境外地表径流量为县内的3座中型水库拦蓄的境外244.2 km2的来水。泗水县现有地表水可利用量中包括:4座中型水库可利用量、小型水库及塘坝可利用量、河道提引水可利用量等。全县地下水源供水工程主要包括机电井取水工程和引泉工程。
根据泗水县现存水利工程及在建或已规划水利工程情况,对规划水平年不同降水保证率下全县可供水总量进行预测,详见表1。

表1 泗水县水资源总量及规划水平年可供水量汇总表 万m3Tab.1 The summary sheet of gross amount of water resources and available water in plan year
3.2 需水量预测分析
根据本县经济社会发展需求,参照水利部门及其他相关部门所做专项规划成果,按照各行业及生活用水定额(充分考虑各行业用水以及土地利用变化情况,对用水定额进行相应的修订),依据本地农作物种植制度和灌溉制度,分别预测规划水平年2020年各行业及生活用水在不同降水保证率下的需水量。见表2。

表2 规划水平年用水需求预测表 万m3Tab.2 the prediction table of water demand in plan year
注:其他指林、牧、渔业需水量。
3.3 水资源供需平衡分析
通过对规划水平年可供水资源量和水资源需求量预测结果对比,进行水资源供需平衡分析。规划水平年水资源供需平衡情况见表3。

表3 规划水平年水资源供需平衡情况表Tab.3 Status table of the balance of supply and demand of water resources in the plan year
由表3可知,规划水平年降水保证率为50%、75%、90%时,全县余缺水量分别为8 223、-120、-7 951 万m3,当降水保证率为75%、90%时出现缺水情况,且降水保证率为90%时缺水较为严重。
由规划水平年用水需求预测表可知,各行业中农业需水量占据总用水量绝大部分。目前泗水县农业灌溉仍为漫灌,水资源浪费严重。为节约水资源,应首先从农业下手,对灌溉设施进行改进,对农作物生长阶段灌水量进行优化配置,提高用水效率,以满足未来农业灌溉水量需求。
4 泗水县农业水资源高效利用分析
4.1 柯布-道格拉斯生产函数模型实例应用
本次研究对泗水县154个农户农田种植情况进行了调查,其中种植粮食作物、经济作物的分别为l32户、113户。粮食作物采用渠道防渗(包括土渠)和低压管道输水灌溉方式分别占样本的58.2%和41.8%。经济作物采用渠道防渗(包括土渠)、低压管道输水和喷、微灌技术分别占样本的34.2%、57.3%和8.5%。
本次研究选择粮食(经济)作物的单位面积化肥和农药投入金额(K)、单位面积投工量(L)、单位面积水费(M)、粮食(经济)作物经济效益单位面积产值(N)等作为C-D生产函数模型中的变量,求出其产出弹性,并且分别在粮食(经济)作物生产函数模型中引入灌溉技术虚变量(J)以反映不同灌溉技术对作物产值的影响[6]。最终建立C-D生产函数模型,建立如下方程:
N=AtKηLθMγJλ
(3)
式中:At代表当前的社会生产水平;η、θ、γ、λ分别为单位化肥和农药投入金额、单位投工量、单位水费、灌溉技术虚变量对于作物单位产值的产出弹性。
通过对数和回归分析处理,最终得出所建回归方程中各变量产出弹性,对比如表4。
从表4可以看出,两种模型中粮食作物水费投入对粮食作物单位面积产值提升的贡献率远小于化肥和农药、劳动投入;经济作物水费投入对经济作物单位面积产值提升的贡献率大于化肥和农药投入,而小于劳动投入;粮食作物水费的产出弹性为经济作物的1/10左右,即灌溉水量对粮食作物单位面积产值提升的贡献率远小于经济作物。通过模型1与模型2的对比发现,粮食作物采用管道输水技术会使作物单位面积产值较渠道防渗技术有所下降,经济作物采用喷、微灌技术和管道输水技术会使作物单位面积产值较渠道防渗技术有所提高,且喷、微灌技术高于管道输水技术。

表4 各变量产出弹性对比表Tab.4 Comparison of output elasticity of each variable
注:表中模型1为采用渠道防渗技术,作为模型2中管道输水技术和喷、微灌技术的参照。
在不考虑所添加的虚拟变量时,粮食作物其他投入要素的产出弹性之和小于经济作物,即各要素投入的增加对粮食单位面积产值增加程度的影响低于对经济作物单位面积产值增加程度的影响。
通过对各要素的产出弹性和不同节水灌溉技术对农作物单位面积产值影响的实例研究可知,在研究区内资金和水资源投入到经济作物获得的产出效益高于粮食作物,应优先考虑经济作物节水灌溉技术资金和物质投入。
4.2 非充分灌溉理论的应用
在用水量及技术资金优先考虑经济作物的情况下,粮食作物用水需求将无法得到满足,因此需要利用非充分灌溉理论对粮食作物灌溉进行水量合理利用研究。
为了充分利用非充分灌溉理论,达到节水及灌溉用水利用效率最高的目的,应对农作物的需水特性及各阶段对缺水的敏感程度进行充分了解。泗水县粮食作物主要为冬小麦和夏玉米,根据以往其他学者的实验研究,冬小麦和夏玉米各生长阶段需水特性及不同灌溉处理情况下粮食产量情况分别如表5、表6。
由表6可知,冬小麦在拔节孕穗、抽穗(雄)开花、乳熟3个阶段进行轻旱处理减产率较低,夏玉米在拔节孕穗轻旱、乳熟期轻旱、拔节孕穗及抽穗开花连旱3种情况下减产率较低。因此,在枯水年份,可根据实际降雨量及供水情况在冬小麦和夏玉米减产率较低的生育期适当减少灌水量,以节约用水保证其他生育阶段充分灌水,使灌溉水量利用效率得到提高。
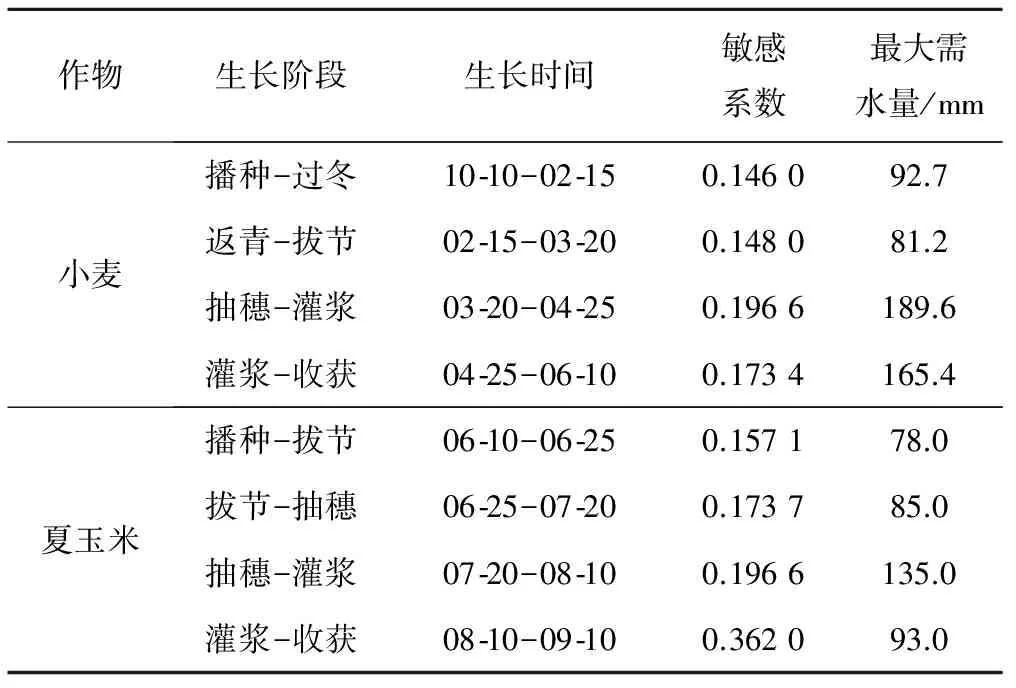
表5 冬小麦和夏玉米各生长阶段需水特性表Tab.5 Characteristics of each growths tage for winter wheat and summer maize
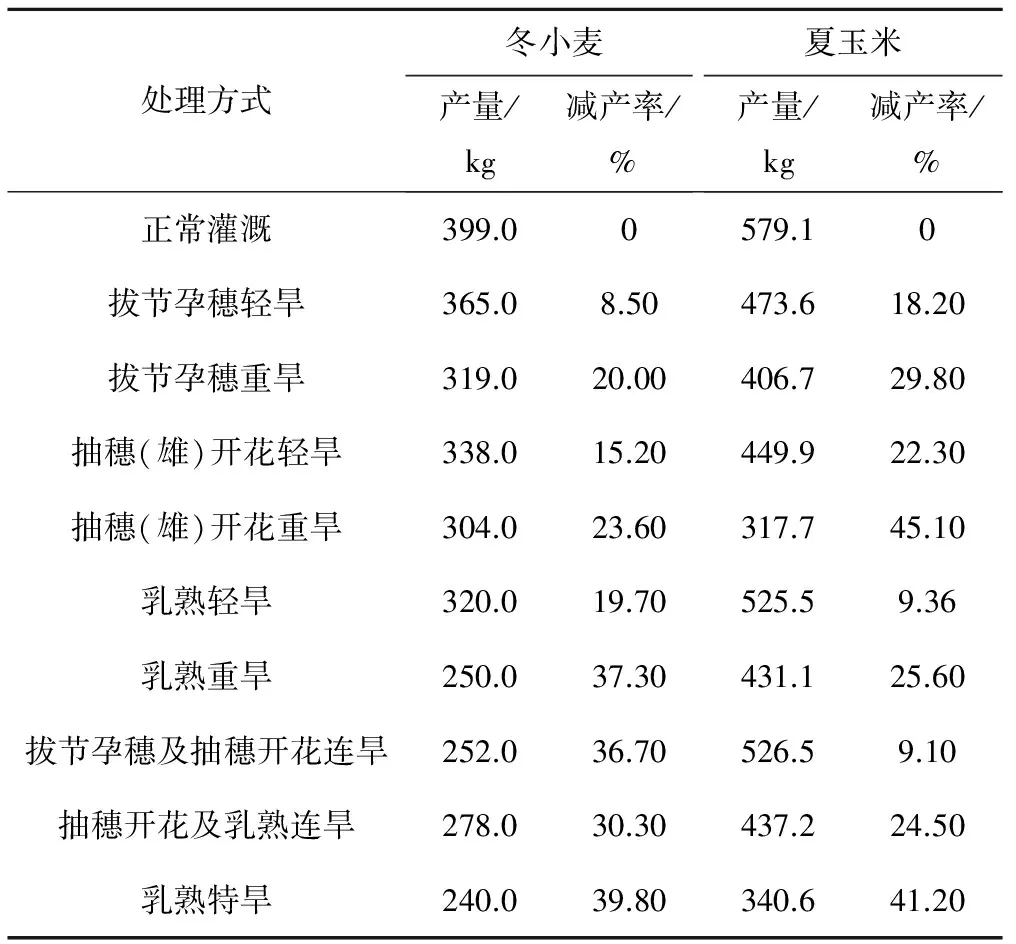
表6 不同灌溉处理情况下冬小麦和夏玉米产量变化情况表Tab.6 The changes of yield of winter wheat and summer maize under different irrigation treatments
本次研究缺乏足够的实验分析,根据现有资料无法求出粮食作物灌水量与作物产量或经济效益之间的函数关系式,因此在非充分灌溉理论的应用中仅能定性的描述,无法在不同降水保证率情况下对粮食作物各生育阶段灌水量做出定量分析,相关研究有待进一步加强。
5 节水灌溉工程总体分布
根据泗水县小型农田水利重点县建设“系统化、规模化、高标准、新技术”的基本原则,结合当地土地及水资源基本情况对泗水县节水灌溉工程总体布局做出了一些规划。工程总体布局如图1。
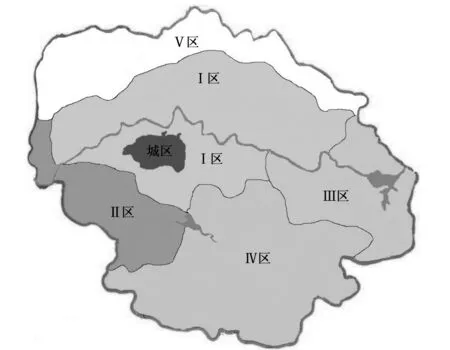
图1 泗水县节水灌溉工程总体布局图Fig.1 General layout of water saving irrigation project in Surabaya County
图1中,Ⅰ区地势平坦,地下水丰富,该区域粮食作物、经济作物相间分布,是泗水县重要的粮食及经济作物产区,该区域内粮田采用高标准管道灌溉技术,果树采用小管出流技术,蔬菜采用膜下滴灌技术;Ⅱ区属于山地丘陵区,土壤瘠薄,作物产量低,主要进行土地治理,提高土壤肥力;Ⅲ区地下水丰富,蔬菜等经济作物种植规模大,该区应发展蔬菜膜下滴灌项目和建设旱作物农业示范基地;Ⅳ区内山地丘陵较多,地表水源分散,利用困难,田间主要种植果树,产量较低,因此该区域适合发展果树微灌项目;Ⅴ区为山地,不适合农业发展,为未规划区。
6 结 语
(1)在未来规划年份降水量偏低的情况下可供水量无法满足各方面的需求,在优先满足生活用水和工业用水需求且农业用水需求占总需水量绝大部分的前提下,农业应实行节水灌溉。
(2)资金和水资源投入到经济作物获得的产出效益高于粮食作物,应优先考虑经济作物节水灌溉资金和物质投入。
(3)根据非充分灌溉理论及其他学者的研究成果可知,在降水较少的情况下,应根据实际降雨量并以粮食作物需水特性和不同生育阶段缺水情况下减产率为参照,对粮食作物进行非充分灌溉,以提高灌溉水量利用效率。
(4)根据泗水县土地利用及水资源基本情况,本文做出了节水灌溉工程总体布局规划,为泗水县节水灌溉项目顺利实施提供了一些建议。
□
[1] 王忠静,马真臻,廖四辉,等. 洪水资源利用经济适度性研究——以海河流域为例[J]. 水力发电学报,2013,(1):11-18.
[2] 王立波. 要素资本结构与企业成长性分析[D]. 山东青岛:中国海洋大学,2010.
[3] 李 晶. 新疆农业增长的技术进步技术效率分析[D]. 乌鲁木齐:新疆大学,2007.
[4] 贺 城,廖 娜. 我国节水灌溉技术体系概述[J]. 农业工程,2014,(2):39-44.
[5] 陈玉民,肖俊夫,王宪杰,等. 非充分灌溉研究进展及展望[J]. 灌溉排水,2001,(2):73-75.
[6] 韩 青. 农业节水灌溉技术应用的经济分析[D]. 北京:中国农业大学,2004.

