基于信息扩散和可变模糊集的石林县旱灾风险评价

张 强，陈志明,2，张 雪(.河海大学商学院，南京 20098；2.河海大学水文水资源与水利工程科学国家重点实验室， 南京 20098)

0 引 言

旱灾是世界上最严重的自然灾害之一，它在持续时间、影响范围、灾害影响等方面位列自然灾害之首[1]。2010-2012 年中国西南地区连续三年特大春旱等都预示着未来的干旱威胁将更大[2]。随着中国经济不断发展，生态环境的易损性和脆弱性增大，导致干旱成灾率和旱灾损失呈明显增加的趋势。

干旱的风险评价已成为国内外学者们研究的热点问题。Tsakiris[3]等在区域干旱评价中采用了一种全新的侦查指数，它包含了除降水外其他的气象参数、潜在蒸散等因素，更适用不断变化的环境。李文亮[4]等采用信息扩散理论对黑龙江省气象干旱灾害进行了风险评估与区划研究分析。陈晓楠[5]等建立了神经网络模型对农业干旱程度进行量化计算，详细地研究了农业干旱的概率分布，并以河南省濮阳市渠村灌区作为实例，计算出该区域的农业干旱程度概率分布。陈家金[6]等利用正态 信息扩散的计算方法，结合东南沿海三省历年的作物干旱受灾面积和成灾面积资料，对该区域进行农业干旱风险评估。杨奇勇[7]等基于干旱风险管理的稳定性、脆弱性和恢复性，同时考虑到区域的应急抗旱水平，以湖南省的14个地州市为研究对象，利用灰色关联聚类法、层次分析法等方法建立评价模型，对湖南农业干旱风险进行了分析。张星[8]等以农业气象自然灾害为研究对象，采用灰色分析方法对其进行评估，根据关联度对灾害轻重程度进行排序，运用GM模型预测了灾害严重年份。

国内外关于干旱风险评估已经取得了非常丰富的研究成果，考虑到干旱灾害的不确定性和随机性，以及小样本和模糊性问题，引入模糊数学领域的信息扩散和可变模糊集理论建立干旱灾害风险评价模型，该模型具有可操作性强、数据需求小等特点。通过对云南省石林县的调研实际情况，从干旱灾害的危险性、敏感性和受损性3个方面出发，选取相应的农业干旱灾害风险评价指标，建立指标体系，将可变模糊评价与信息扩散相结合的模型运用到石林县旱灾风险评估中，为该县应对农业干旱灾害提供了决策依据。

1 干旱风险评价指标体系

1.1 研究区简介

本文以云南省石林县的农业旱灾为研究对象，时间跨度为2000-2010年共11年。2008 年以来，石林县出现了自有气象记录以来最严重的干旱灾害，旱灾发生范围之广、干旱程度之重、持续时间之长、损失之重都是历史罕见的。对农业生产造成了很大的危害，严重制约了农业生产和社会经济的发展，造成全县5.1 万人、2.6 万头大牲畜饮水困难，农作物受灾面积13 717.9 hm2，成灾面积7 282.9 hm2，绝收面积2 560 hm2。

1.2 干旱风险评价指标体系

在进行干旱灾害风险评价时，指标体系的选取尤为重要。一般来说，合理的干旱评价指标不仅应能准确地描述干旱的程度、范围和起止时间，而且应包含明确的物理机制，充分考虑到降水、蒸发、土壤等因素的影响。根据自然灾害系统理论，干旱灾害风险取决于致灾因子的危险性、孕灾环境的敏感性和承灾体的受损性。本文从这三方面出发，选取相应的干旱风险评价指标，如图1所示。

图1 农业干旱灾害风险评价指标体系Fig.1 Agricultural drought disaster risk evaluation system

1.3 干旱灾害风险评数据来源

通过实地调研及查阅《云南统计年鉴》、《云南省水利统计年鉴》、《云南省水资源公报》、《云南省旱情简报》、《抗旱规划初稿》等资料，获得了2000-2010年11年间石林县的评价指标特征值。由于篇幅所限，表1只列出部分指标数据。

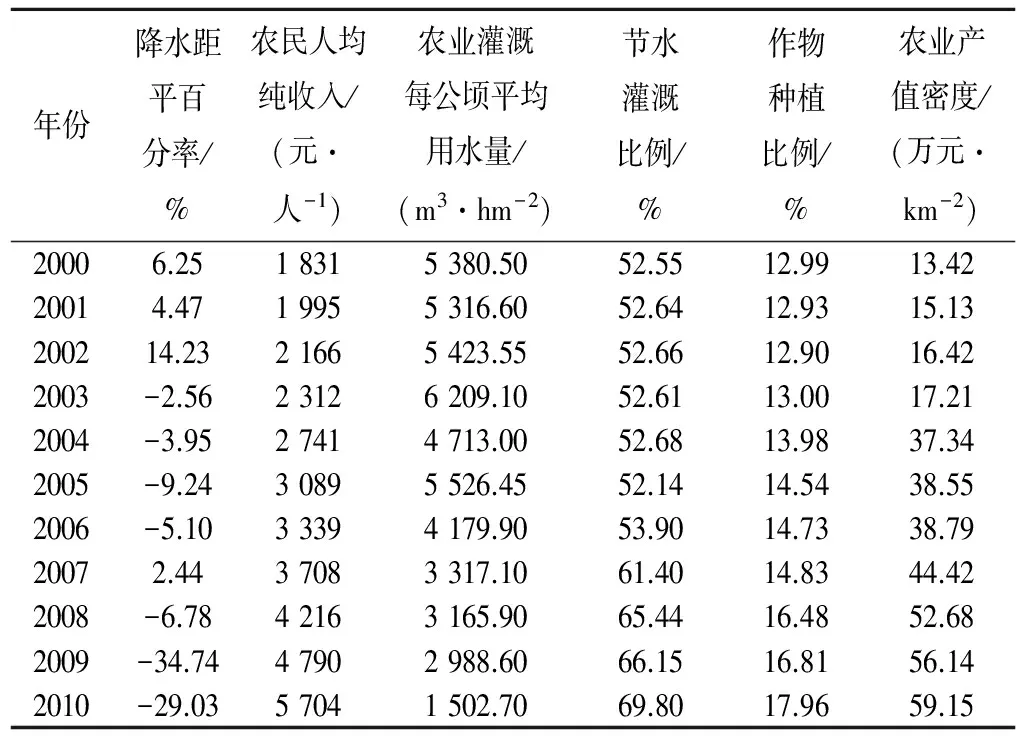
表1 云南省石林县2000-2010年的农业旱灾风险评价指标特征值Tab.1 Agricultural drought risk assessment eigenvalues of Yunnan Shilin County during 2000-2010 years

2 模型构建

基于干旱灾害风险评价随机性和不确定性等特点，引入模糊信息处理中的信息扩散方法[9](Information Diffusion Method)和模糊数学领域的可变模糊集理论[10](Variable Fuzzy Sets，VFS)建立基于信息扩散-可变模糊(IDM-VFS)耦合的干旱灾害风险评价模型，有效解决风险评价中的小样本、信息不足和模糊性等问题，其建模主要过程如下。

2.1 信息扩散的计算步骤

信息扩散是一种通过适当的扩散模型将样本集值化的模糊数学处理方法，它能够优化利用样本的模糊信息。本文选用正态扩散模型，其基本计算步骤如下：

设某一评价指标的离散点为X={x1,x2,…,xn}，xi(i=1,2,…,n)为样本点的观测值，其论域U为U={u1,u2,…,um}，uj(j=1,2,…,m)为论域内的某个取值。

通过正态扩散函数fi，将样本点xi所携带的信息扩散给论域U中的每一个取值uj：

(1)

(i=1,2,…,n,j=1,2,…,m)

式中h为扩散系数，计算公式如下：

(2)

式中：a、b分别为样本中的最小值、最大值。

为了使每个集值样本地位相同，对扩散函数fi(uj)进行归一化处理，令：

(3)

则归一化后的扩散函数gi为：

(4)

在所有样本都经过以上处理后，计算经信息扩散后推断出的观测值为uj的样本个数q(uj)和各uj上的样本总数Q：

(6)

则样本落在uj处的频率为：p(ui)=q(uj)/Q，也就是灾情为uj的概率，而指标值超过uj的超越概率为：

(7)

计算出各评价指标xi在其论域内的取值uj出的超越概率P(uj)，按照旱情等级的超越概率分级标准，求出各评价指标对应旱情等级的临界值，得到旱情等级划分标准。

2.2 模糊可变评价法的步骤

基于可变模糊集理论的模糊可变评价法通过模型并变化其参数组合，科学地计算出干旱评价等级，提高干旱风险评价结果的可信度。模糊可变评价法主要包括以下几个步骤：

(1)生成指标特征值矩阵。设有n个自然灾害样本组成的样本集，X=(x1,x2,…,xi,…,xn)，依据r个指标特征值对样本进行识别。第i个样本的特征用r个指标特征值表示：xi=(x1i,x2i,…,xsi,…,xri)T，则样本集可以用r×n阶指标特征值矩阵表示：X=(xsi)r×n，其中：xsi为第i个样本的第s个指标特征值，s=1,2,…,r，i=1,2,…,n。

(2)建立指标标准特征值矩阵。样本集根据r个指标按c个级别的指标标准特征值进行识别，则有r×c阶指标标准特征值矩阵：Y=(ysh)r×c，ysh为级别h关于指标s的标准特征值，h=1,2,…,c。

(3)确定吸引域、范围域及点值矩阵。参照指标标准值矩阵和待评价地区的实际情况确定干旱灾害可变集合的吸引域矩阵与范围域矩阵，Iab=([ash,bsh])和Icd=([csh,dsh])。根据干旱灾害风险度分为c个级别的实际情况确定吸引域[ash,bsh]中DA(xsi)h=1的点值Msh的矩阵M=(Msh)。

(4)计算指标分级相对隶属度矩阵。判断样本特征值xsi在Msh点的左侧还是右侧，根据如下公式计算差异度DA(xsi)h：

x落入M点左侧时的相对差异函数模型为：

(8)

x落入M点右侧时的相对差异函数模型为：

(9)

D(u)=-1x∉[c,d]

(10)

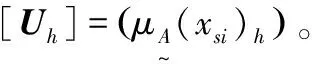
(5)确定各指标权重。

ω=(ω1,ω2,…,ωr)

(6)计算综合相对隶属度。

(11)

式中：iu′h为非归一化的综合相对隶属度；α为模型优化准则参数；ωs为指标权重；r为识别指标数；p为距离参数，p=1为海明距离，p=2为欧氏距离。

α与p可采用不同的组合参数，即α=1,p=1；α=1,p=2；α=2,p=1；α=2,p=2 4种取值。

(7)计算级别特征值进行分级评价。根据模糊概念在分级条件下最大隶属度原则的不适应性，计算级别特征值对样本进行级别评价，如下式。

H=(1,2,…,c)·U

(12)

3 云南省石林县农业旱灾风险评价

将建立的IDM-VFS模型运用到云南省石林县的农业干旱灾害风险评价中。首先利用信息扩散模型确定各风险评价指标的分级标准。以干旱评估通用的分级方法，将干旱等级划分为五个等级，分别是无旱、轻旱、中旱、重旱和特旱。各评价指标等级划分标准确定后，采用可变模糊评价法对云南省石林县进行农业干旱灾害风险评价。石林县农业干旱风险评价指标等级划分标准见表2。

目前，确定指标权重的方法主要包括客观赋权法和主观赋权法两大类。客观赋权法根据实际问题的样本数据，采用一定方法对指标权重进行计算；而主观赋权法主要取决于决策人的主观判断，评判者根据自身经验确定各指标的重要程度。两类方法各有利弊，因此，文章将两种方法结合起来确定各评价指标的权重，首先采用熵权法计算出各指标的数学权重，然后利用网络分析法(ANP)确定指标的经验权重，最终将两套权重进行加权组合，从而求得每个指标的权重值。计算求出的农业干旱灾害评价各指标权重值如表3所示。

表2 干旱风险评价指标等级划分标准Tab.2 Drought risk assessment classification standard

表3 基于熵权法和ANP法的云南省石林县农业旱灾风险评价指标权重Tab.3 The agricultural drought risk assessment index weight of Yunnan Shilin County based on entropy and ANP method

根据表2建立石林县可变集合的吸引域矩阵Iab与范围域矩阵Icd以及点值Msh的矩阵。判断样本值与点值的位置关系，计算相对差异度D(xsi)h、指标对风险等级的相对隶属度μA(xsi)h。采用第3节确定的各指标权重，根据公式采用不同的参数组合，可以计算得到非归一化的综合相对隶属度向量iu′h，归一化后得到综合相对隶属度矩阵U。石林县各风险子系统评价指标相对隶属度矩阵如表4所示。

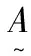
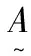
最后通过变换参数α、p的取值，进行级别特征值的计算，可得各区县干旱风险危险性、敏感性和受损性3个子系统的平均级别特征值。石林县各年的农业干旱风险值如表5所示。

由表5可见，石林县2009年干旱灾害的危险性最高，其次为2010年、2005年。2009年以来，南盘江流域部分地区降雨较正常水平严重偏少，且气温持续偏高，土壤和植被含水量低，水库塘坝蓄水得不到有效补充，从而导致干旱难以缓解。干旱灾害的脆弱性总体为逐渐减弱的趋势，这是由于农民收入、农业灌溉设施、抗旱投入水平以及应对旱灾能力均逐渐增强，从而降低了干旱灾害的脆弱性。2010年的易损性最高，石林县的作物受旱率达到35.19%，因旱成灾率达31.74%，是11年中最为严重的一年；其次是2002年，作物受旱率达到34.21%，因旱成灾率达29.28%。2000-2011年平均来看，石林县的危险性风险值为2.19，敏感性为3.42，受损性为3.04。

根据计算出云南省石林县的干旱灾害子系统的风险特征值，利用各子系统的综合权重值可以得到区域的农业干旱灾害综合风险等级，即：

表4 石林县各子系统评价指标的相对隶属度矩阵Tab.4 Each relative membership degree matrix of subsystem index in Shilin County

R=W×H

(13)

式中：R为区域旱灾综合风险值；W表示各子系统综合权重向量；H就是各区县的子系统风险特征值向量，最终得到石林县最终的综合风险等级为3级。

4 结 语

本文综合考虑其危险性、脆弱性和易损性3个因子，构建了干旱灾害风险评价指标体系，形成干旱灾害风险评估系统。基于信息扩散方法，确定评价指标的风险等级划分标准。利用可变模糊评价模型，对干旱灾害进行风险评

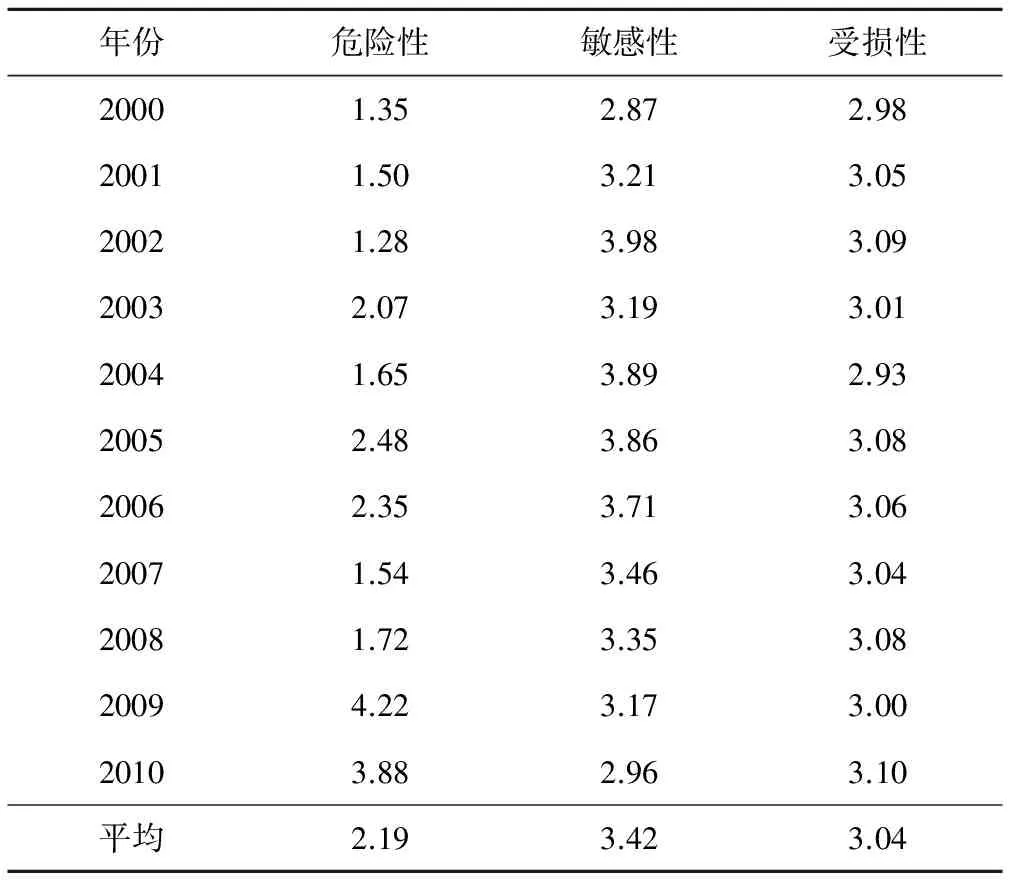
表5 石林县农业旱灾风险评价系统的干旱风险值Tab.5 The drought risk value of Shilin County about agricultural drought risk assessment system

价，建立基于信息扩散——可变模糊集理论的旱灾风险评价模型。以云南省石林县进行实证研究，采用IDM-VFS模型计算出该县2000年-2010年的农业干旱风险水平，分别对危险性、脆弱性和易损性进行子系统风险分析，最后得到综合风险等级。

□

[1] Sam Lake P. Drought and aquatic ecosystems: effects and responses[M]. Oxford, UK: John Wiley and Sons Ltd, 2011.

[2] 吴 迪,裴源生,赵 勇,等.湄公河流域农业干旱主要影响因素分析和预估[J]. 农业工程学报,2012,28(8):1-10.

[3] Tsakiris G, Pangalou D, Vangelis H. Regional drought assessment based on the Reconnaissance Drought Index (RDI)[J]. Water Resources Management, 2007, 21(5): 821-833.

[4] 李文亮, 张冬有, 张丽娟. 黑龙江省气象灾害风险评估与区划[J]. 干旱区地理, 2009,32(5):754-760.

[5] 陈晓楠,黄 强,邱 林,等.基于混沌优化神经网络的农业干旱评估模型[J].水利学报,2006,37(2):247-252.

[6] 陈家金,王加义,林 晶,等. 基于信息扩散理论的东南沿海三省农业干旱风险评估[J]. 干旱地区农业研究, 2010,28(6):248-251.

[7] 杨奇勇, 毛德华. 湖南省农业干旱水资源风险评价[J]. 湖南师范大学自然科学学报, 2008,31(1):125-129.

[8] 张 星,陈 惠,周乐照. 福建省农业气象灾害灰色评价与预测[J]. 灾害学, 2007,22(4):43-45.

[9] 欧阳蔚,于艳青,金菊良,等. 基于信息扩散与自助法的旱灾风险评估模型——以安徽为例[J].灾害学, 2015,30(1):228-234.

[10] 陆志强,李吉鹏,章耕耘,等. 基于可变模糊评价模型的东山湾生态系统健康评价[J].生态学报, 2015,35 (14):1-17.