底端约束对封闭式坝体防渗墙应力计算的影响
高 江 林
(江西省水利科学研究院,江西省水工安全技术研究中心,南昌 330029)
0 引 言
混凝土防渗墙具有适用地层条件强、防渗性能可靠等特点,在各类防渗处理工程中得到了大量应用[1-4],尤其是在我国新一轮实施的病险水库除险加固工程建设中,已成为堤坝防渗加固的主要措施[5-7]。随着土石坝和堤防加固工程建设的不断深入以及除险加固工程建设的周期化实施,混凝土防渗墙在水利工程建设中的应用也将日益增多。
防渗墙是堤坝防渗体系的关键所在,防渗墙的应力变形直接关系到防渗墙结构本身的安全,从而影响整体防渗和工程安全。因此,准确计算防渗墙的应力变形对于安全、合理地设计使用混凝土防渗墙具有重要意义。有限元法能够较好实现各种复杂因素的相互影响及复杂边界条件的模拟,是土石坝及防渗墙应力变形计算的主要方法之一,并为规范[8]所推荐。同时,有限元法也具有计算结果受所选用本构模型、计算参数、边界条件、计算方法等因素影响较为明显的特点[9,10]。因此,了解和掌握不同因素对计算结果影响的大小和规律,并根据具体工程条件选择合理的模拟方法非常重要。
土石坝坝体防渗加固工程中,除具有深厚覆盖层的情况外,大多采用封闭式坝体防渗墙直接嵌入基岩,然而目前针对此类防渗墙的研究较少。加固工程中的大坝多为运行几十年的老坝,增设坝体防渗墙时大坝需先后经历库水位放空(或降低)-坝体成槽-墙体施工-完工蓄水等过程。由于土体固结程度、荷载、边界条件及施工过程的不同,防渗墙的承载性状与一般新建土石围堰或坝基中的防渗墙存在一定差异。因此,进行土石坝加固工程中封闭式坝体防渗墙的有限元应力变形计算,关键是选择符合实际工程条件的数值模拟方法和计算参数,墙体底端约束方式的选择就是其中的一个重要问题。
本文针对土石坝加固工程中增建的封闭式坝体防渗墙,分别采用固定约束和接触约束两种墙底端约束形式对防渗墙的应力变形进行有限元计算,分析两种约束形式对计算结果的影响与规律情况。
1 计算内容
1.1 计算模型与计算参数
图1为一般地基上建设有封闭式坝体防渗墙的均质土坝,墙厚0.6 m,正常蓄水位25.0 m。具体计算条件如图1所示,有限元网格划分如图2所示。
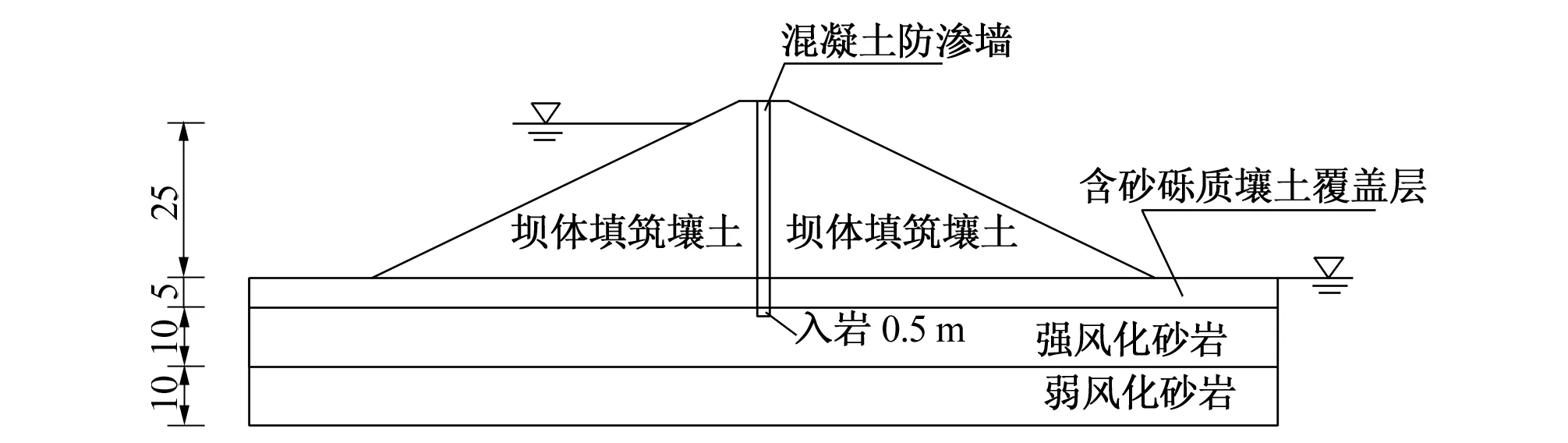
图1 计算模型(单位:m)Fig.1 Computation model
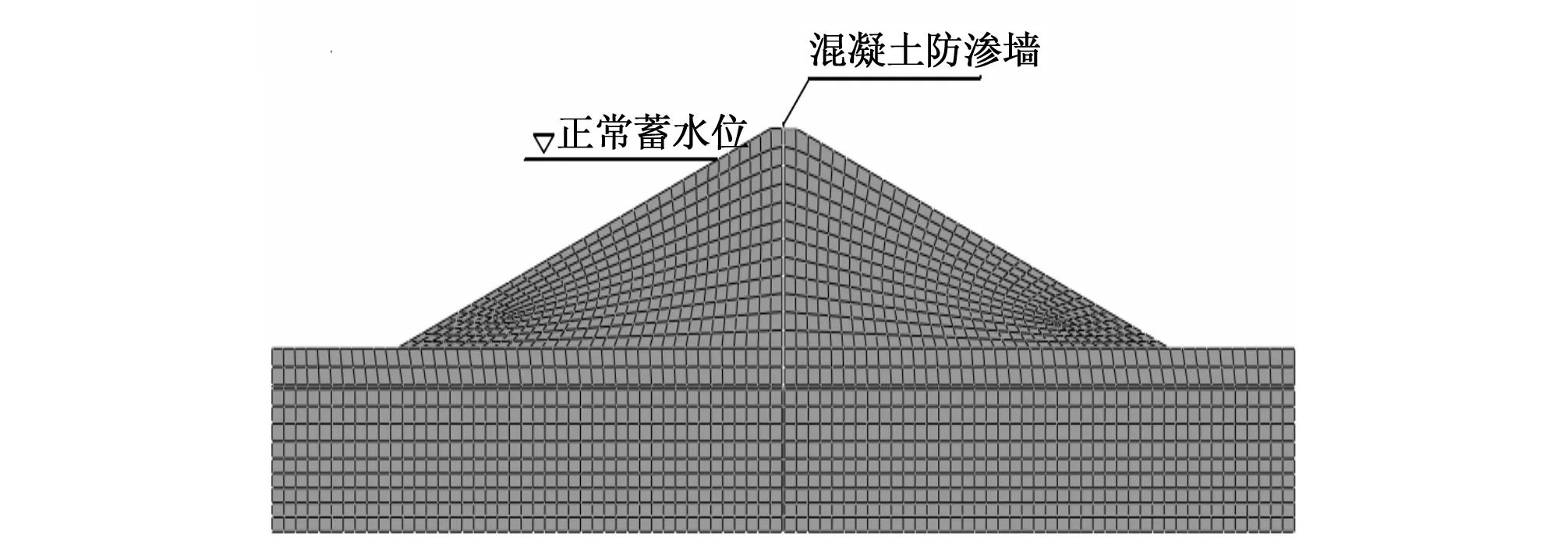
图2 有限元网格图Fig.2 Finite element mesh
本文采用ABAQUS有限元软件对不同底端约束形式的防渗墙应力变形进行分析,考虑坝体土固结已基本完成,且坝高和蓄水位较低,土体应力水平及其变形模量随荷载变化不大,为简化计算,防渗墙混凝土采用线弹性模型,土体采用Mohr-coulomb弹塑性模型,部分材料计算参数如表1。
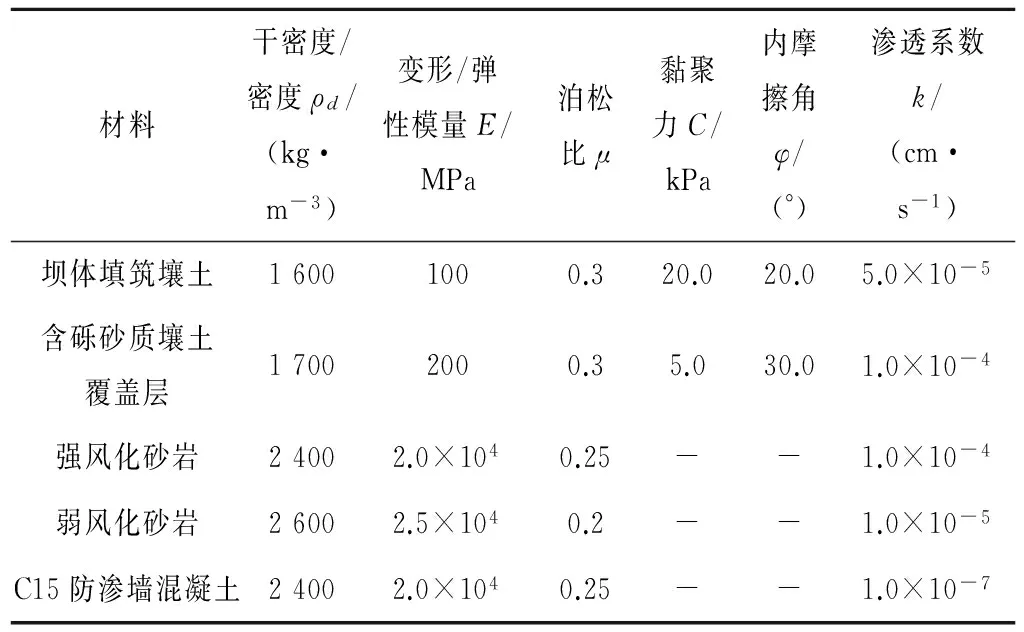
表1 部分材料有限元计算参数Tab.1 Computation parameters of partial materials
1.2 有限元计算的约束方法
本文采用考虑渗流场与应力场耦合、墙-土接触共同作用的有限元耦合数值模型[11]进行防渗墙应力变形计算,分析墙体底端采用接触约束和固定约束两种形式对计算结果的影响。
1.2.1接触约束
防渗墙与坝基的接触约束采用接触单元来实现,包含接触面的法向作用和切向作用。防渗墙与坝基采用接触约束时,入岩部分墙体(3个面)全部采用接触单元与基岩进行接触约束。
(1)法向作用。接触面的法向模拟采用硬接触,即坝体和墙体只有在压紧状态时才能传递法向压力p,若墙-土之间有间隙时则不能传递法向应力。
(2)切向作用模型。接触面的切向作用采用库仑摩擦模型,用摩擦系数μt来模拟在两个表面之间的摩擦行为。当接触面有法向接触压力时,接触面可以传递切向应力,并设定极限剪应力:
τcrit=μtp
(1)
1.2.2固定约束
防渗墙与基岩之间采用固定约束时,两个接触面上对应节点间无相对移动,且具有相同位移和孔压。防渗墙与坝基采用固定约束时,入岩部分墙体(3个面)全部采用固定约束。
2 墙体底端约束形式对墙体应力变形的影响
对防渗墙底端采用固定约束和接触约束时的墙体应力变形进行对比分析,本文有限元计算以拉应力为正。考虑墙底沉渣影响,墙体侧面和底面与基岩的接触摩擦系数μt分别取为0.58和0.4。
2.1 墙体主应力对比分析
两种底端约束形式计算的防渗墙最大主应力(拉应力)和最小主应力(压应力)分布如图3、图4所示。
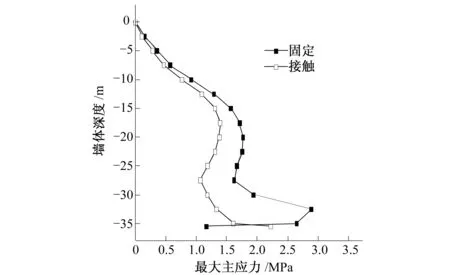
图3 墙体最大主应力分布Fig.3 Max principal stress distribution of wall

图4 墙体最小主应力分布Fig.4 Min principal stress distribution of wall
由图3可以看出,总体上,采用固定约束时有限元计算的墙体最大拉应力大于采用接触约束的结果,最大拉应力分别为2.88和2.22 MPa,相差约30%。两种情况所计算的最大拉应力值出现的位置不同,采用固定约束时最大拉应力出现在基岩面附近,而采用接触约束计算的最大拉应力出现在墙体底部。
根据图4,除底部压应力外,采用固定约束时的墙体最大压应力大于采用接触约束的计算结果,最大压应力分别为1.56和1.95 MPa。与最大拉应力类似,采用固定约束时的最大墙体压应力出现在基岩面位置,而采用接触约束时的最大墙体压应力出现在墙体底部。相对于墙体承载能力而言,两种约束形式计算的墙体最大压应力水平较低,说明封闭式坝体防渗墙的应力分析应重点考虑其拉裂破坏的可能性。
综合图3和图4,对于土石坝加固工程中的封闭式坝体刚性防渗墙,不同底端约束形式对墙体应力的有限元计算结果(应力大小、分布规律)影响明显。
2.2 墙体弯矩
两种底端约束形式计算的墙体弯矩分布如图5所示。
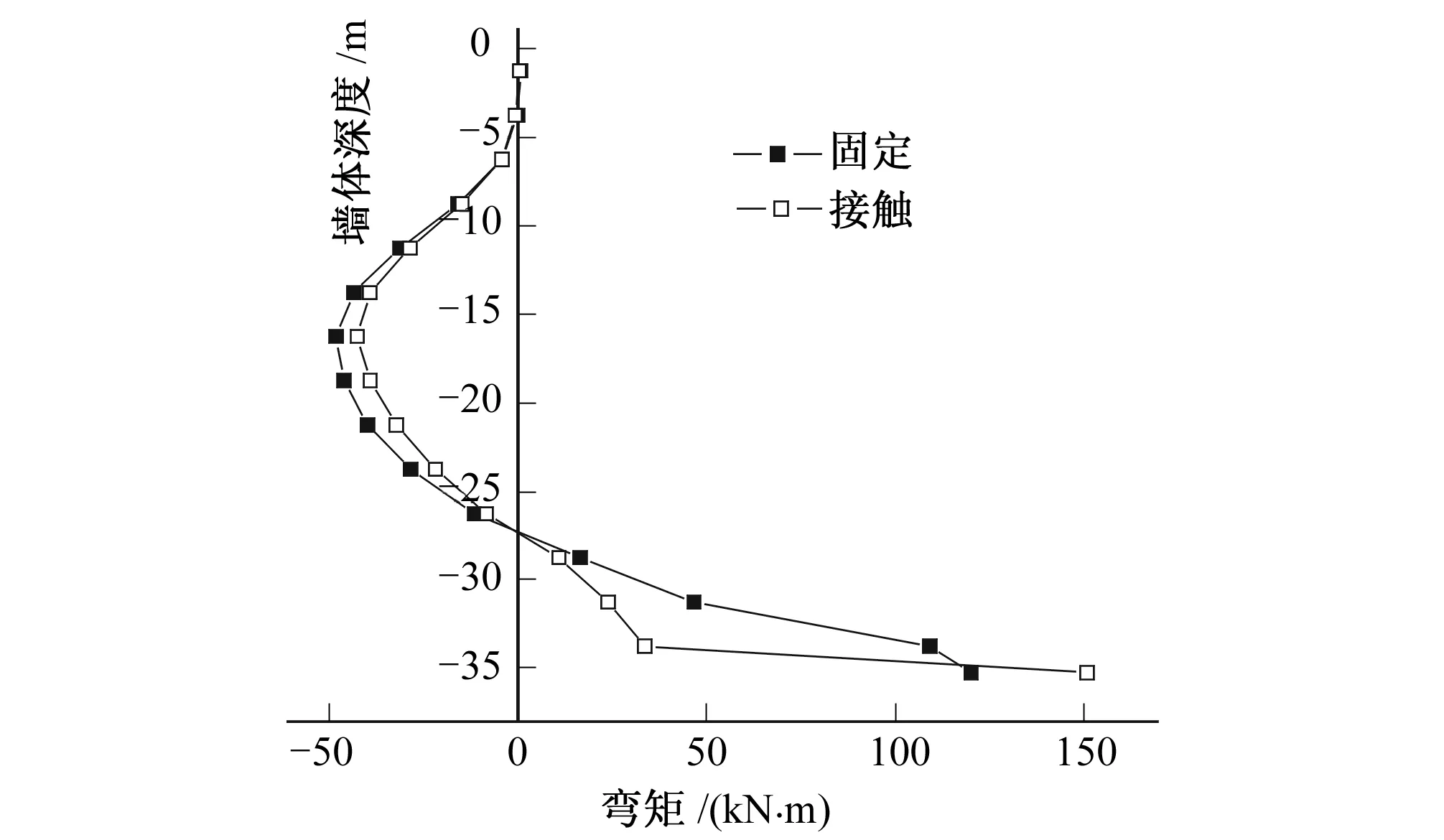
图5 墙体弯矩分布Fig.5 Bending moments distribution of wall
由图5可知,两种约束形式的最大弯矩均出现在墙体底部,除墙体底部外,固定约束计算的墙体弯矩均为大于采用接触约束的计算结果。最大弯矩值分别为120.2 kN·m(固定约束)、151.0 kN·m(接触约束),相差约25%左右。
土石坝除险加固工程中混凝土防渗墙多为水下成槽施工,实际施工过程中往往会形成一定量的墙底沉渣(规范[12]允许的孔底淤积厚度为不大于100 mm),且由于加固工程中的封闭式坝体防渗墙主要受水平荷载作用[11],此类防渗墙受基岩面位置的嵌固作用会更为明显。综合两种约束形式的墙体应力和弯矩分布情况,对于墙底沉渣较厚的影响,采用固定约束的计算结果与实际情况更为吻合。
2.3 墙体变形
不同底端约束形式计算的墙体水平位移分布如图6所示。
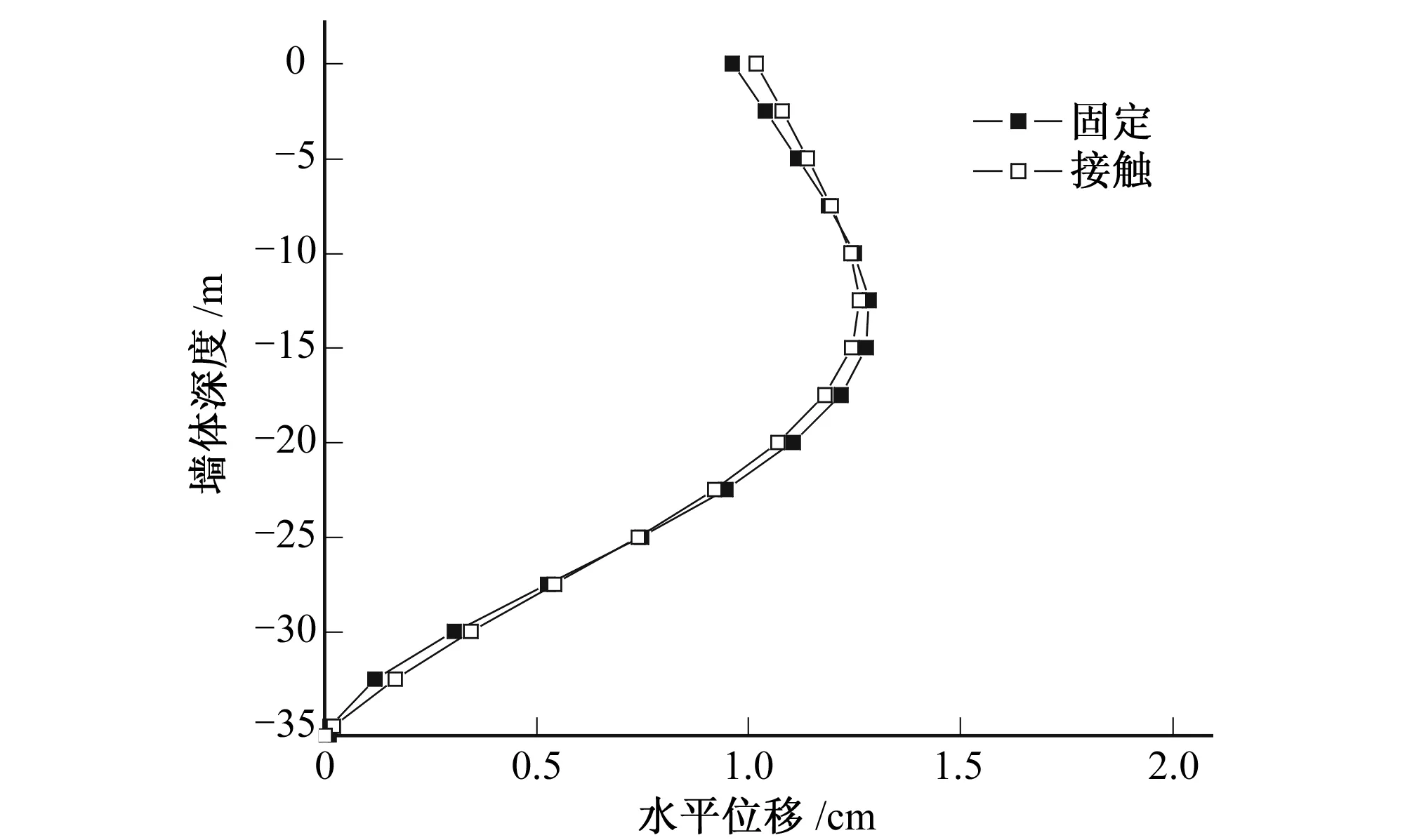
图6 墙体水平位移Fig.6 Horizontal displacements of wall
由图6可以看出,采用固定约束时,中间大两端小的位移趋势更明显,最大水平位移为1.28 cm,采用接触约束计算时的最大位移为1.26 cm,相差1.6%,且位置相同。总体上两种约束形式计算的墙体水平位移分布基本一致,不同约束形式对墙体位移计算结果的影响较小。
综合两种约束形式计算的墙体应力、弯矩和变形分析,采用固定约束进行防渗墙应力的有限元分析时,计算结果更偏于安全,也更符合有墙底沉渣的防渗墙实际受力情况。
2.4 不同基岩类型时墙底端约束影响比较
为分析不同基岩类型条件下两种底端约束形式对防渗墙应力计算结果的影响,墙底基岩弹性模量分别取为2.5×104MPa、1.0×104MPa、5.0×103MPa。
2.4.1墙体最大拉应力分析
不同基岩弹性模量时两种约束形式计算的墙体最大主应力分布如图7所示。
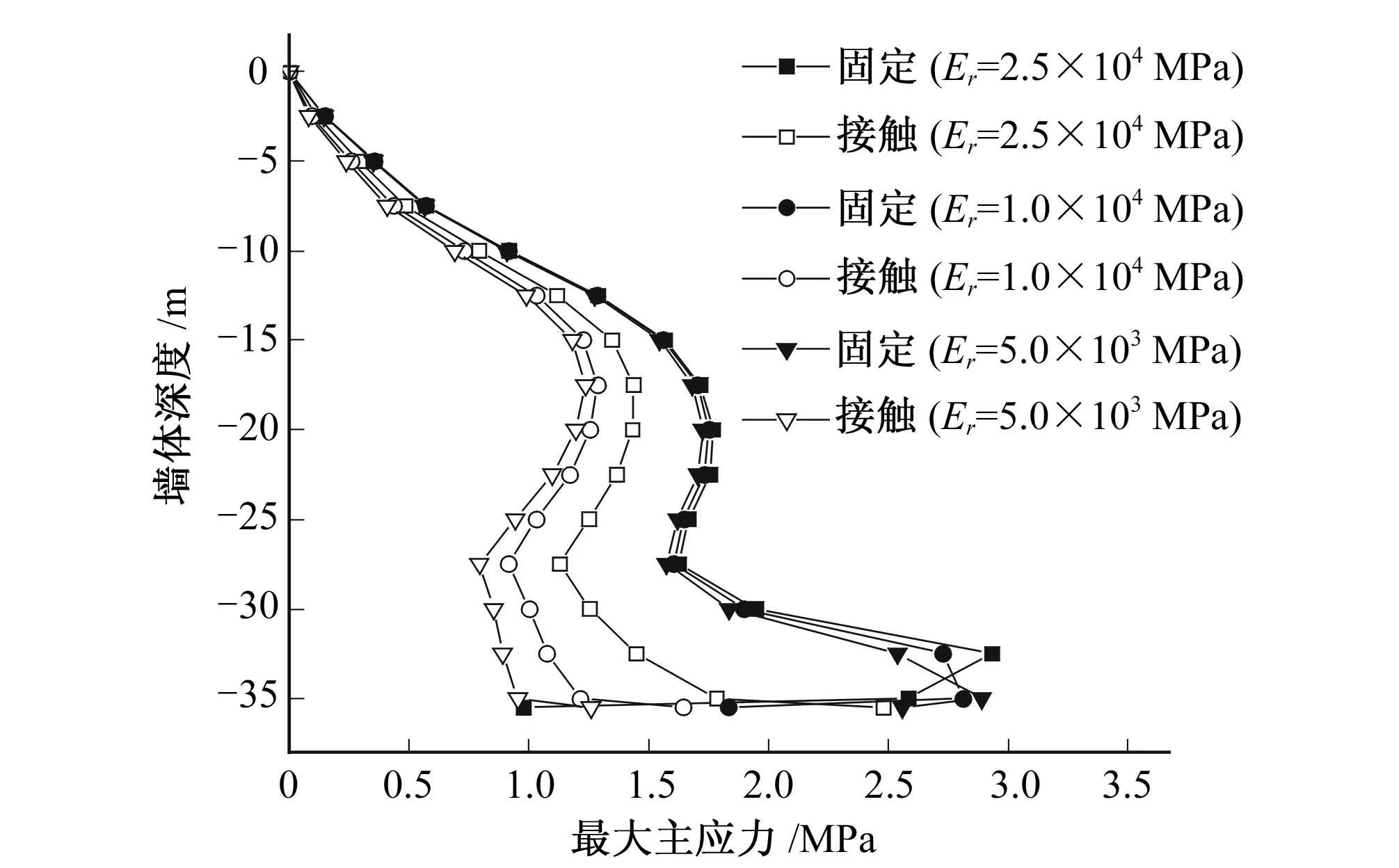
图7 最大主应力Fig.7 Max principal stress
根据图7,墙体底端采用固定约束时,不同基岩弹性模量时(2.5×104MPa、1.0×104MPa、5.0×103MPa)的最大拉应力均出现在基岩面附近,分别为2.93、2.81、2.89 MPa。总体上表现为基岩弹模越大,基岩面及以上部位的墙体应力越大,但墙体底部最大拉应力则随着基岩弹模增大逐步较小(基岩对墙底部的嵌固作用增加),墙体最大拉应力位置逐步往上移。不同基岩弹性模量的最大拉应力相差0.12 MPa(相差约4.3%),采用固定约束时不同坝基弹性模量对墙体最大拉应力的影响较小。
墙体底部采用接触约束时,不同基岩弹性模量时的最大拉应力均出现在墙体底部,最大拉应力分别为2.48、1.65、1.26 MPa。最大拉应力随基岩弹模减小而迅速减小,最大相差1.22 MPa(相差约1倍)。与采用固定约束相比较,采用接触约束时不同坝基弹性模量对墙体应力计算结果的影响更加明显。
此外,根据相同基岩条件下两种约束形式的对比可以看出,采用固定约束计算的最大拉应力大于采用接触约束时的计算结果。当基岩弹模较大时,两种约束形式计算的最大拉应力相差0.45 MPa(相差约18%);而当基岩弹模较小时,不同约束计算的最大拉应力相差1.63 MPa(相差约129%)。因此,基岩弹性模量越小,不同底端约束形式的选取对防渗墙应力计算结果的影响越大。
2.4.2墙体最大压应力分析
不同基岩弹性模量时两种约束形式计算的墙体最小主应力分布如图8所示。
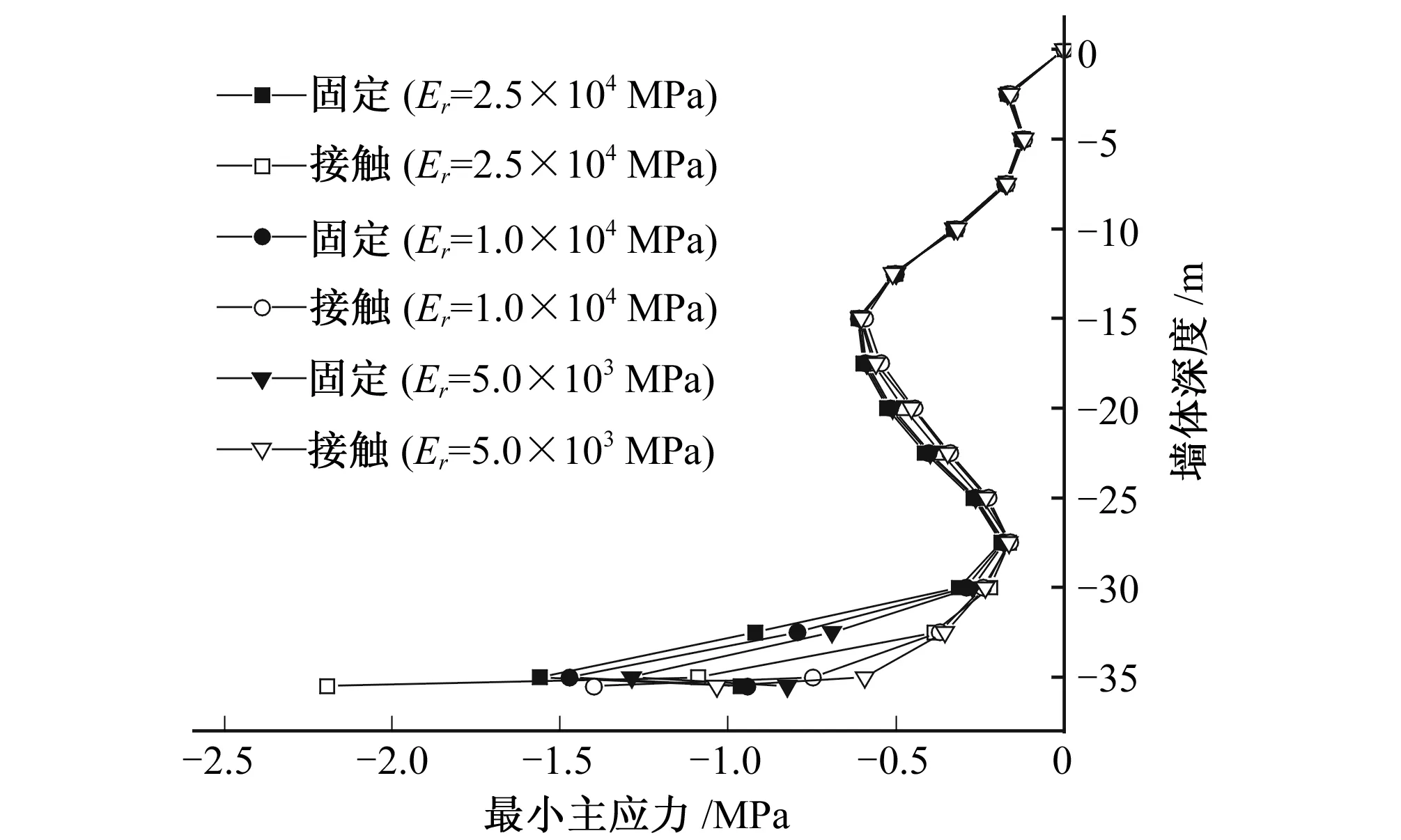
图8 最小主应力Fig.8 Min principal stress
根据图8可以看出,与最大拉应力相对应,不同基岩弹模时采用固定约束计算的最大压应力同样出现在基岩面位置,分别为1.56、1.47、1.29 MPa,随基岩弹性模量减小而减小,最大差值为0.27 MPa(约相差21%)。
墙体底部采用接触约束时,不同基岩弹性模量时的最大压应力均出现在墙体底部,分别为2.19、1.40、1.03 MPa,随基岩弹性模量减小而减小,最大差值为1.16(约126%)。
从相同基岩条件下两种约束形式计算结果的对比可以看出,当基岩弹模较大时(Er=2.5×104MPa),固定约束计算的最大压应力小于接触约束的计算结果;当基岩弹模较小时(Er=2.5×103MPa),固定约束计算的最大压应力大于接触约束时的计算结果。总体上,接触约束计算的最大压应受基岩弹性模量的影响更为明显。
综上分析,对于墙体拉应力而言,不同基岩类型上墙底端采用固定约束时的计算结果大于采用接触约束的计算结果,且基岩弹性模量越小,两种约束形式的计算结果偏差越大。总体上,采用接触约束时不同基岩弹模模量对墙体应力的影响要大于采用固定约束时的计算结果。
3 结 论
(1)对于土石坝加固工程中的封闭式坝体刚性混凝土防渗墙,采用不同底端约束形式对墙体应力的有限元计算结果影响明显。总体上采用固定约束计算的墙体应力大于采用接触约束的计算结果,尤其是对于墙体承载更为关键的拉应力。相对而言,不同约束形式对墙体变形的计算结果影响较小。
(2)固定和接触两种约束形式在不同刚度基岩中表现出不同的影响特征。采用固定约束计算时不同基岩弹性模量对墙体应力的影响较小;而采用接触约束计算时不同基岩弹性模量对应力影响明显,墙体应力随基岩弹模减小而减小。因此,进行墙体应力的有限元计算时,应根据基岩特性和墙体承载条件选择合理的底端约束形式和计算参数。
□
[1] 王清友,孙万功,熊 欢. 塑性混凝土防渗墙[M]. 北京:中国水利水电出版社, 2008.
[2] 徐杨青, 刘国锋, 盛永清. 深基坑嵌岩地下连续墙隔渗效果分析与评价方法研究[J]. 岩土力学, 2013,34(10):2 905-2 910.
[3] Hinchberger S, Weck J, Newson T. Mechanical and hydraulic characterization of plastic concrete for seepage cut-off walls[J]. Canadian Geotechnical Journal, 2010,47(4):461-471.
[4] Singh A K,Mishra G C,Samadhiya N K,et al. Design of a rigid cutoff wall[J]. International Journal of Geomechanics, 2006,6(4):215-225.
[5] 庞 琼, 王士军, 谷艳昌,等. 土石坝垂直防渗加固措施综述[J]. 水利水运工程学报, 2014,(4):28-37.
[6] 邵 磊, 余 挺, 贾宇峰,等. 堆石坝心墙内增设加固防渗墙的结构特性研究[J]. 人民长江, 2014,45(7):48-51.
[7] Balian Sebouh. Cut-off wall construction[J]. International Water Power and Dam Construction, 2007,59(2):42-44.
[8] DL/T 5395-2007, 碾压式土石坝设计规范[S].
[9] 介玉新, 周厚德. 防渗墙的弯矩计算[J]. 岩石力学与工程学报,2009,28(6):1 213-1 219.
[10] 郦能惠,米占宽,孙大伟. 深覆盖层上面板堆石坝防渗墙应力变形性状影响因素的研究[J]. 岩土工程学报,2007,29(1):26-31.
[11] 高江林,陈云翔. 基于渗流与应力耦合的防渗墙与坝体相互作用的数值模拟[J]. 水利水运工程学报. 2013,(2):58-63.
[12] SL633-2012, 水利水电工程单元工程施工质量验收评定标准-地基处理与基础工程[S].

