交互式两阶段分位值水资源系统规划模型

孔祥铭，郝振达，黄国和(. 华北电力大学区域能源系统优化教育部重点实验室，北京 006；. 中央财经大学资产管理处，北京 0008)

作为经济社会可持续发展的重要保证，水资源的可持续利用至关重要。水资源短缺问题日益严重，极大影响了社会经济的发展和人民生活水平的提高[1,2]。为了提高水资源利用效率，解决水资源供需平衡的问题，需要建立一套合理的水资源配置方案。同时，水资源系统中存在随机性、模糊性、灰色性等多种不确定性，如降雨径流的不确定性、各个用水行业单位用水量的收益和需水量不确定性等[3,4]。这些不确定性来源于水资源系统的复杂性，给水资源管理增加了难度。因此，利用不确定性规划方法解决水资源系统规划问题具有重要的意义。

目前，常用的不确定规划方法包括区间规划方法、模糊规划方法和随机规划方法[5-7]。然而，大部分不确定性优化方法只关注解决表现形式为单一不确定性的问题，缺乏对多重不确定性的相关分析。事实上，在水资源系统中，有些参数为区间数，但其上下界可能带有模糊信息，无法用确定的值表示，这就造成了参数的双重不确定性。另外，水资源管理者对于系统收益的偏好也需要体现在水资源规划模型中。因此，本文将分位值优化方法引入随机规划模型中，建立了交互式两阶段分位值优化(ITFO)模型。通过采用分位值优化方法体现决策者对水资源系统收益的偏好，同时采用交互式两阶段随机方法对缺水的损失进行追索。

1 模型构建

1.1 交互式两阶段随机模糊规划模型

在水资源规划问题中，决策者基于水资源的实际情况，制定向用水行业的水资源配置目标。由于不确定性事件的存在，水资源配置目标往往和实际供水量有很大出入。如果水资源配置目标大于实际给水量，那么会造成水资源的浪费。反之，如果水资源配置目标小于实际给水量，则会造成经济上的损失。因此，有必要构建水资源优化配置模型，为决策者提供水资源配置方案。同时，作为现实生活实际存在的误差源，来自主观估计的模糊信息也有必要体现在模型中。交互式两阶段随机模糊规划(ITSFP)模型[8]可以解决上述问题。

(1)

满足

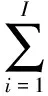
θE1+(1-θ)E2,∀k=1,2,…,Kt

Ximax≥X±i≥Y±i,∀i=1,2,…,m,k=1,2,…,Kt

Y±ik≥0,∀i=1,2,…,m,k=1,2,…,Kt

1.2 分位值优化方法

ITSFP模型可以解决约束两边参数的双重不确定性，但是无法处理目标函数的模糊信息，最终得到的系统收益值是模糊的，而不是确定性的数值，这样增加了决策方案比较选取的难度。分位值优化(FO)方法可以有效解决目标函数中存在模糊不确定性的问题，从而弥补ITSFP模型的不足。给定一个模糊规划模型：

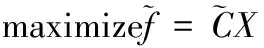
(2)

满足

AX≤B

X≥0

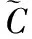
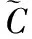
(3)

1.3 交互式两阶段分位值优化模型

为了解决水资源系统中的双重不确定性，同时将目标函数和约束中的模糊信息确定化，本文将FO方法引入ITSFP模型中，开发了一种交互式两阶段分位值优化(ITFO)模型。

(4)

从属于：

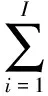
θE1+(1-θ)E2,∀k=1,2,…,K

Ximax≥X±i≥Y±ik,∀i=1,2,…,m,k=1,2,…,Kt

Y±ik≥0,∀i=1,2,…,m,k=1,2,…,K

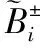
ITFO模型的解为f±opt=[f-opt,f+opt]、Xiopt和Y±ikopt=[X-ikopt,X+ikopt]。

2 案例分析

本文将建立的ITFO模型应用于水资源系统规划例子中，验证其有效性和实用性。该系统的用户包含城市用水、工业用水和农业用水，以系统收益最大化为目标，结构如图1所示。由于水资源系统的不确定性和复杂性，预计分配给城市用水、工业用水和农业用水的水资源量T±i分别为[1.8,2.4]、[2.3,3.7]和[3.0,5.8] (106m3)。水资源系统的经济数据如表1所示，包含了当水资源分配目标得到满足时的单位净收益和没有得到满足的经济惩罚。来水量的信息如表2所示。

图1 水资源系统结构图Fig.1 The framework of water resources system

表1 经济指标和水资源分配目标 $/m3Tab.1 Economic data and water allocation target

表2 不同概率情景下的径流量Tab.2 Streamflow data under various probabilities of occurrences

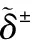
3 结果分析

将ITFO模型应用于上述水资源系统规划问题中，得到对应不同可信度和分位值的解。图2为不同可信度θ和分位值pne水平下的系统收益。在每个可信度θ水平下，不同的分位值pne输入将导致系统收益的不同，反之亦然。例如，在给定可信度θ取值分别为0.3、0.5、0.7、0.9和分位值pne取值分别为0.4、0.6、0.8、1.0的条件下，当θ=0.3时，系统收益上界的上下界分别为587.75×106$和561.92×106$；系统收益下界的上下界分别为168.11×106$和155.71×106$。另外，由结果可知，可信度θ与系统收益上界呈现反比关系，与系统收益下界呈现正比关系；分位值pne与系统收益呈现反比关系。当给定分位值pne时，随着可信度θ的增大，系统收益值减小，同时系统收益区间变小，不确定性降低。

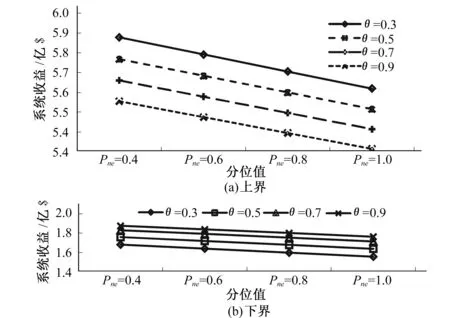
图2 系统收益Fig.2 System benefits

图3给出了θ=0.5和pne=0.6时的优化的水资源分配量。在低流量时，城市用水不存在缺水情况，而工业用水和农业用水实际水资源分配量的下界都为0，即有可能分不到水。在径流量为中水平下，工业用水和农业用水也存在缺水情况。在高水平下，只有农业用水的水资源分配量得不到满足。以上结论可以得出，水资源最先分配给城市用水，其次为工业用水，最后为农业用水。这是因为相比于工业用水和农业用水，城市用水可以带来更高的收益，同时当水资源分配量得不到满足时，城市用水单位缺水量带来的经济损失更高。因此，为了获得最大的系统收益，决策者会承诺给城市用水更多的水资源分配量。

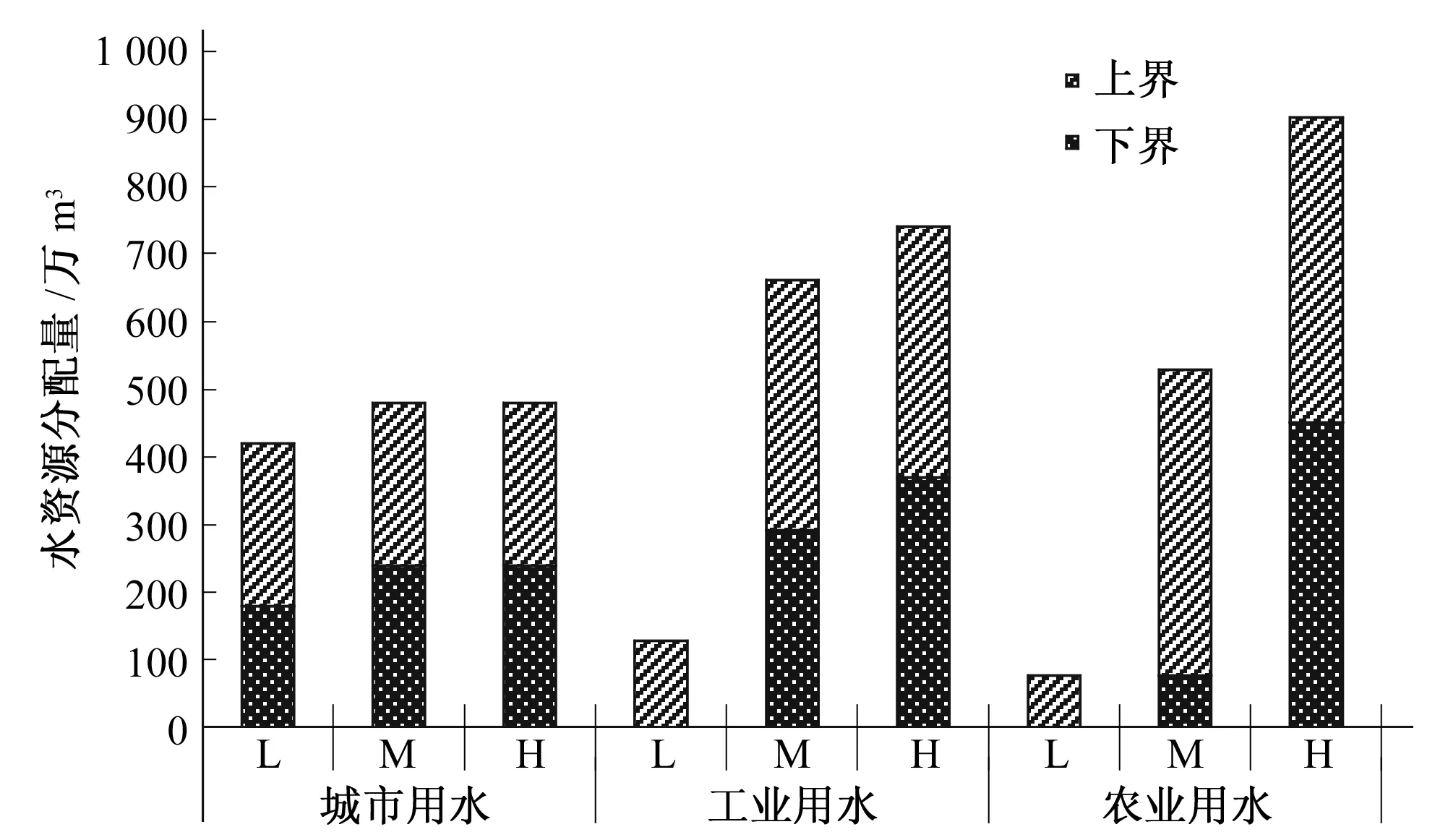
图3 θ=0.5和pne=0.6时的优化的水资源分配量Fig.3 The optimal amount of water allocation under θ=0.5 and pne=0.6

4 结 语

本文开发了一种交互式两阶段分位值优化(ITFO)模型。该模型不但可以解决约束两边参数的双重不确定性，而且可以处理目标函数的模糊信息，最终得到不同可信度和偏好下的系统最优解。本文将ITFO模型应用于水资源系统规划问题，结果表明，ITFO模型可以得到不同可信度θ和分位值pne水平下的系统收益值及水资源分配量。水资源管理者可以依据自己的偏好，从这些决策方案中选取可行的水资源系统规划措施。

□

[1] 赵喜富, 茅 樵, 曹升乐,等. 济南市“五库连通工程”水资源优化配置研究[J]. 中国农村水利水电, 2015,(7):47-53.

[2] 解河海, 查大伟. 大藤峡水利枢纽水资源优化调度研究[J]. 中国农村水利水电, 2015,(6):48-51.

[3] 曾雪婷, 李永平. 不确定性规划在水资源管理中的运用与优势[J]. 水利发展研究, 2013,(7)37-39.

[4] Kong X M, Huang G H, Fan Y R, et al. Maximum entropy-Gumbel-Hougaard copula method for simulation of monthly streamflow in Xiangxi river[J]. China. Stochastic Environmental Research and Risk Assessment, 2015,29(3):833-846.

[5] Huang G H, Loucks D P. An inexact two-stage stochastic programming model for water resources management under uncertainty[J]. Civil Engineering and Environmental Systems, 2000,17(2):95-118.

[6] Liu B. Uncertainty Theory[M]. Springer Berlin Heidelberg, 2007.

[7] Kong X M, Huang, G H Fan, et al. A duality theorem-based algorithm for inexact quadratic programming problems: Application to waste management under uncertainty[DB/OL]. Engineering Optimization, 2015, Online.

[8] Wang S, Huang G H. Interactive two-stage stochastic fuzzy programming for water resources management[J]. Journal of Environmental Management, 2011,92(8):1 986-1 995.

[9] Dubois D, Prade H. Possibility Theory: An Approach to Computerized Processing of Uncertainty[M]. New York, NY, USA: Plenum Press, 1988.

[10] Torabi S A, Hassini E. An interactive possibilistic programming approach for multiple objective supply chain master planning[J]. Fuzzy Sets and Systems, 2008,159(2):193-214.