备耕头水地土壤入渗参数的线性预报模型

岳海晶 ，樊贵盛

(太原理工大学水利科学与工程学院，太原 030024)

0 引 言

土壤水分入渗是指降雨或灌溉过程中水分通过地表进入土壤的过程，决定着降雨或地面水转化成土壤水的过程以及在土壤剖面中的空间和时间上的分布，从而影响农田灌溉质量和灌溉效果。备耕土头水地是指农田播种后需进行第一次灌溉的土地。其特点是表土疏松，灌溉时随着灌溉水入渗过程的进行，灌溉水进入土壤，并且伴随着表层土的浸没、崩塌和湿陷等过程，尤其是黄土更是如此。这意味着在土壤水分的入渗过程中土壤骨架发生变形，变形趋势是表土的密度由疏松变密实，即土壤干密度由小变大，灌溉前后土壤密度有较大的差异。但是，《土壤水动力学》中对土壤水分运动的研究只限于固相骨架不变形的多孔介质，即认为土壤骨架不变形[1]。然而在人们的研究和生产实践中发现，随着土壤含水量的变化，土壤干密度在不断变化，进而引起土壤水分的入渗能力及其他水分运动过程的变化。解文艳，樊贵盛[2]等针对土壤结构对土壤入渗能力的影响进行了详细分析。针对这一现象，黄传琴，邵明安[3]对干湿交替过程中的土壤胀缩特性进行了研究，分析了胀缩过程中土壤的容积变化与土壤含水率的关系以及土壤的胀缩特性；陈亮，卢亮[4]等研究了土壤干湿循环过程中体积变形特性，阐述了含水量的变化对土壤体积的影响机制；樊贵盛，韩永鸿，孔令超，李尧[5]等人对土壤脱水过程中结构与含水量的关系进行了定量研究，明确了脱水过程中土壤密度与含水率存在着二次函数关系。基于上述研究成果，备耕翻松土壤在头水以后表层土壤的含水量急剧增加，导致了表层土壤结构的密实度增加，土壤入渗能力降低[6]。由于备耕土灌溉前地表土壤结构疏松，渗透性大，如果按照备耕土灌溉前的土壤基本理化参数进行灌溉后土壤水分入渗能力的预测，势必造成入渗能力预测值大于入渗能力实际值，如果依据预测值来指导农田灌溉势必造成水量的浪费，因此为了更为实际地预测备耕后第一次灌溉土壤水分的入渗能力以便在灌溉过程中节约水资源，本文以模型参数物理意义较为明确的Kostiakov三参数入渗经验模型为表述土壤水分入渗过程的模型，基于黄土高原区备耕头水地土壤入渗试验以及相对应的土壤基本理化参数，采用线性回归分析的方法建立备耕头水地灌溉前后两种条件下的土壤水分入渗模型参数与土壤基本理化参数间的多元线性数学模型，通过模型预测精度的对比分析，确定和提出能更好反映备耕头水地土壤水分入渗模型参数的预报模型，为使试验结果便于应用到实际农业活动中，本文还建立了考虑土壤结构变形土壤入渗模型参数与不考虑结构变形时土壤入渗模型参数间的关系，利用备耕头水地灌溉前的土壤理化参数间接推求其土壤入渗参数的方法，据此对黄土高原区备耕头水地土壤的入渗参数进行预测。

1 材料与方法

1.1 土壤条件

本文涉及的大田土壤入渗试验区域涵盖山西省大同至运城八市十六个县区。山西地处黄土高原地区，气候干燥，日照充足，南北差异性较大，山西省境内土壤类型丰富，有棕壤土、褐土、栗钙土和栗褐土、黄绵土、红黏土等多种类别；土壤质地有砂土、壤土、黏壤土、黏土等多种类型；土壤结构复杂多样，有团粒状、网粒状、块状，片状、柱状等多种类型[7]。为保证土壤入渗试验的结果能够准确反映试验区的土壤入渗特性，每个县区选取2～4个试验地点，供试土壤选取非冻融翻松土样(以构造备耕头水地条件)，土壤密度在0.858～1.725 g/cm3之间；体积含水量变化范围在5.2%～42.3%之间；土壤砂粒变化在9.66%～72.48%，粉粒变化在12.32%～64.10%，黏粒变化在5%～23.56%范围内；土壤有机质(0～20 cm)的变化在0.55%～6.59%。供试土壤质地类型、结构、含水量、有机质等基本囊括山西省境内所有土壤，试验点分布广泛，数据代表性很强。

1.2 试验设备及试验方法

本次大田土壤入渗试验采用外环直径为64.4 cm，内环直径26.0 cm，内外环高度均为25 cm的双套环入渗仪来获取试验区土壤水分入渗数据。试验前将设备预埋设在深度为20 cm的上部土层中，入渗环下环深度到达犁底层。为控制内、外环积水入渗水头始终保持为2 cm需安装自制的水位控制器，试验过程中内环供水装置用量筒。大量试验表明，90 min前大田非饱和土壤入渗率已达到相对稳定阶段，因此，本次试验采用90 min为入渗试验结束时间。

为建立入渗模型的参数与土壤常规理化参数间的定量关系，本次试验除需获取根据试验结果推求的土壤各时段入渗率外，还需获取土壤基本理化参数数据如各层土壤粒径百分比、土壤密度、体积含水量和有机质含量等。采用烘干称重法获得土壤重量含水量，再结合土壤密度计算出体积含水量；采用100 cm3环刀切割未经扰动的自然状态土壤，使土样充满环刀，烘干称量进而计算出单位体积烘干土质量；土壤质地的测定采用传统的比重计法，获取土壤砂粒、粉粒、黏粒的相对含量；用重铬酸钾容量法测定土壤，获取土壤有机碳的含量进而确定有机质含量。

此外，加水后翻松土地表土壤(0～20 cm)密度会发生变化，为获取此时的地表土密度，选取囊括所有试验土壤质地范围的9种土进行试验，得到头水后的地表土密度，并得出头水前后土壤密度的增加量与黏粒含量的关系，通过内插法获取试验区地表土壤密度的增量从而得到头水后土壤密度。

1.3 数据样本建立

大田土壤入渗试验方法成熟，试验数据准确性高，能够达到90%以上，样本数据资料具有很高的可靠性，根据已测大田土壤入渗试验数据以及土壤各常规理化参数，过滤掉奇异点以及错误明显的数据，选取包含山西省境内所有土壤类型的60组数据作为模型样本，并随机抽取5组数据对预测模型结果进行检验。建立的样本数据包括：双套环入渗仪法获得的90 min内各时段的入渗率，以及根据入渗率利用Origin软件拟合出的Kostiakov三参数入渗模型的参数K、α、f0；土壤0～10、10～20、0～20、20～40 cm土层的灌溉前土壤密度以及0～10、10～20、0～20 cm范围内的灌溉后土壤密度；0～10、10～20、0～20、20～40 cm土层的体积含水量； 0～20、20～40 cm范围内的土壤粒径百分比；0～20 cm范围内土壤有机质含量。所有样本数据来自非冻融期非盐碱地的翻松土壤，将其中的4组样本数据列于表1。

2 备耕土头水后入渗模型参数线性预报模型的建立

2.1 预测模型结构

在满足精度要求的条件下，相较于其他模型来说线性模型的建模较简单，应用方便，可以大大简化工作量，更适合于普通农民和基层管理机构进行或指导农业生产活动。因此，本文利用有较好代表性的入渗试验数据样本，采用线性回归法，建立Kostiakov三参数入渗经验模型的3个参数的线性预报模型。预报模型结构采用如下形式：

Y=β0+β1X1+β2X2+β3X3+…+βnXn

(1)

式中：Y为预测值，包括Kostiakov三参数入渗模型的K、α、f0；βi为模型回归系数；Xi为第i个影响因素，包括常规土壤理化参数：土壤质地、干密度、含水量和有机质含量等；n为变量的个数。

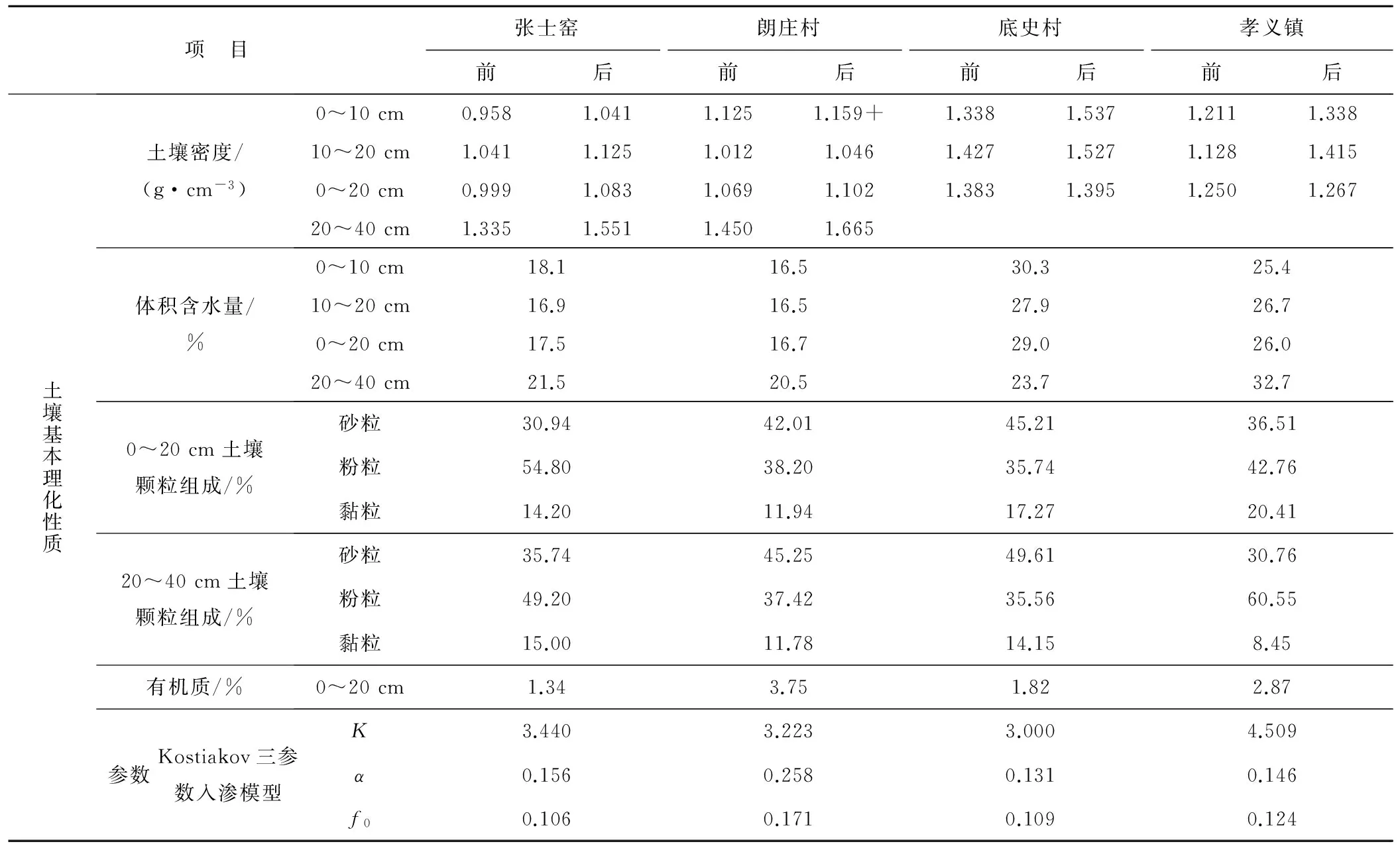
表1 部分试验地大田土壤入渗数据

2.2 预测模型参数

目前国内外研究学者建立了多种土壤入渗模型，本文选取较为常用的物理意义较为明确且使用较为方便的Kostiakov三参数入渗模型来描述土壤水分入渗过程。

i(t)=Kt-α+f0

(2)

式中：i(t)为时刻的入渗速率；K为入渗系数，指入渗开始后第一个单位时间末扣除f0后的累积入渗量；α为入渗指数，能够反映土壤入渗速度的衰减速度；f0为土壤相对稳定入渗率，即单位土壤势梯度下饱和土壤的入渗速度或非饱和土壤入渗达到相对稳定阶段的入渗速度。

为了对比分析灌溉前后密度的增加对土壤入渗参数预报模型精度的影响，分两种情况对入渗参数进行预报，密度增加后预报的入渗模型参数为K、α、f0；密度增加前预报的入渗模型参数为K′、α′、f′0。

2.3 预测模型的输入变量分析

本文所确定的预测变量为Kostiakov三参数入渗模型的3个参数K、α、f0，前人的研究结果表明[8,9]，土壤常规理化参数对3个预测参数K、α、f0的影响层次和个数不同。定性分析结果认为，0～20 cm层次范围内的土壤理化参数对入渗系数K和K′产生的影响最为显著，由入渗系数的物理意义可知，在开始入渗的第一个单位时段内，水分入渗通常只能达到土壤犁底层之上一定厚度的土层，除此之外第一时段内的入渗历时时间较短，地表结构还未发生显著变化，因此与灌溉后密度关系不大；土壤0～20 cm层次范围内的理化参数对入渗指数α和α′有较大影响；对于土壤相对稳定入渗率f0和f′0而言，因其表示的是土壤水分入渗达到相对稳定阶段时的参数，此时土壤水分已入渗到犁底层以下，并在地表形成了一定厚度的饱和含水层，因此与含水量的关系不大，但与表层土壤密度密切相关；土壤机械组成即粒径百分比含量对3个参数的影响显著，由于黏粒变化范围较小，不易反映对参数的影响程度，选取砂粒和粉粒含量来反映土壤质地对入渗参数的影响。通过以上初步分析，影响3个预测参数K、α、f0的土壤层次和理化参数初步确定如表2。

表2 模型参数线性预报模型影响因素

注：○-影响变量；-不影响变量。

2.4 各模型参数的线性预报模型结构

根据以上初步确定的模型结构、输入变量参数的个数和层次、预测变量参数，针对所有理化参数从数学和数理统计角度进行大量回归运算，从提高拟合度及选取对模型有显著影响的理化参数两方面来剔除与模型关系较小的理化参数，最终建立表3所示的灌溉入渗前后的Kostiakov三参数入渗模型参数线性预报模型结构。

由于灌溉过程中备耕疏松地表(0～20 cm)土壤密度产生的结构变化对于K和K′的影响不存在，因此土壤结构发生变形时，K和K′的预报模型相同。

表3 各模型参数线性预报模型结构

式中：γ1、γ2、γ3分别为灌溉前0～10、0～20、20～40 cm土壤干密度，g/cm3；γ′1、γ′2分别为灌溉后0～10、0～20 cm土壤干密度，g/cm3；θ1、θ2、θ3分别为0～10、0～20、20～40 cm土壤体积含水率，m3/m3；ω1、ω2分别为0～20 cm砂粒、粉粒含量，%；G为0～20 cm有机质含量，%。

由于灌溉过程中备耕疏松地表(0～20 cm)土壤密度产生的结构变化对于k和k′的影响不存在，因此土壤结构发生变形时，k和k′的预报模型相同。

2.5 各参数线性预报模型系数的回归

(1)回归方程系数。利用前面选定的60组数据样本，依据数理统计学最小二乘法原理，将样本数据代入已建模型结构进行回归分析，得到的回归结果列于表4。

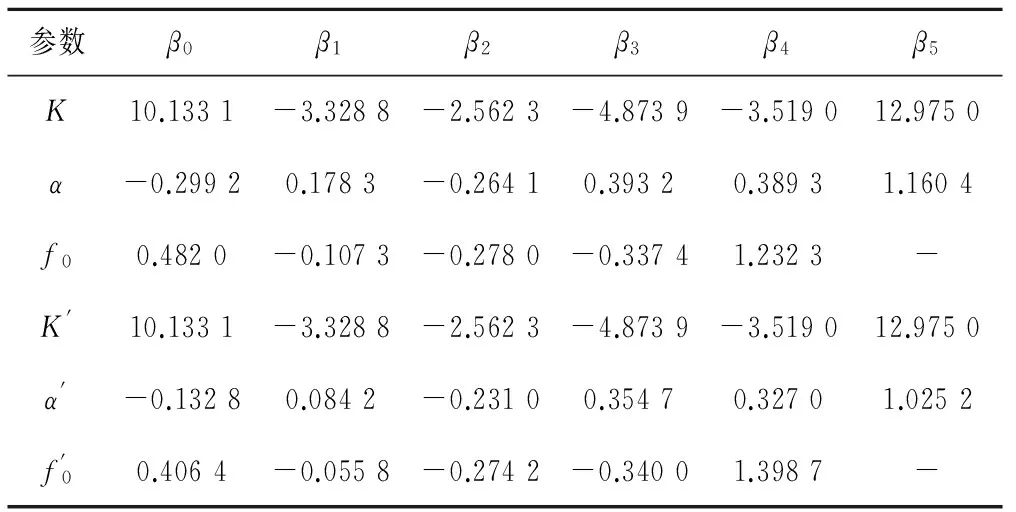
表4 三参数入渗模型回归参数结果

(2)模型显著性检验。采用方差分析法对回归模型的显著性进行检验，首先计算样本 值，然后与给定显著水平(α=0.05)下对应的Fα(m,n-m-1)值相比较，其中n为样本数，m为变量数。模型的显著性结果列于表5。

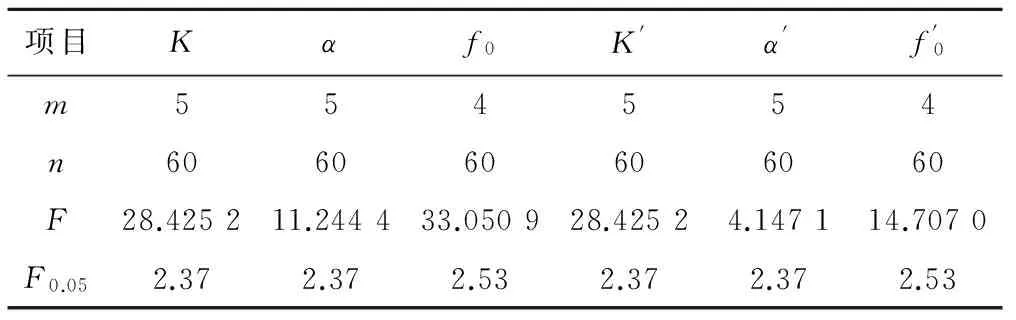
表5 模型回归显著性检验结果

据表5所得结果，入渗模型参数的F值(4.147 1～33.050 9)均比对应的F0.05值(2.37～2.53)大，由此可以判断所建立的线性回归模型是显著的。

(3)回归系数的显著性检验。回归系数显著性检验的目的是为了验证模型变量是否与预测变量有显著关系，将由样本数据计算得到的 值与 (a=0.05)值比较从而判断其显著性。模型回归系数显著性检验结果如表6。

由表6可以看出，若考虑灌水过程中土壤结构的变化，即地表密度增加，所有输入变量的|Ti|均大于t0.025值，由此可以判断模型的输入变量对模型预测值的影响均是显著的。若不考虑灌水过程中土壤结构的变化，即地表密度增加，对于预测参数α′，0～20 cm土层密度的回归系数β1(1.900)、0～20 cm土层粉粒含量的回归系数β4(1.770 5)的|Ti|都小于t0.025值，表明输入参数对预测值的影响不显著，此结果也同时表明，考虑灌水过程中土壤结构的变化(土壤密度的增加)的理念是正确的。

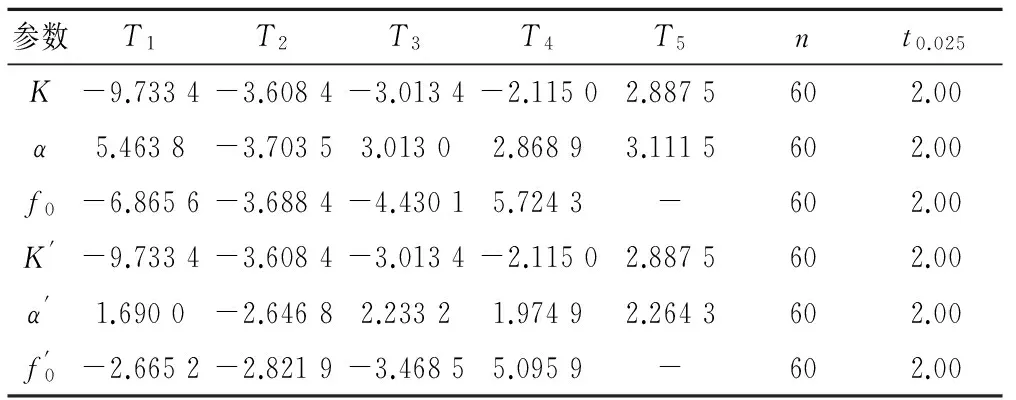
表6 回归系数显著性检验结果

综上研究分析，可建立利用灌溉后密度直接预测备耕头水地入渗参数的方法，模型结构如下：

i(t)=Kt-α+f0

(3)

K=10.133 1-3.328 8γ1-2.562 3θ1-4.873 9ω1-

3.519 0ω2+12.975 0G

(4)

α=-0.299 2+0.178 3γ2-0.264 1θ20.393 2ω1+

0.389 3ω2+1.160 4G

(5)

f0=0.482 0-0.107 3γ1-0.278 0ω1-

0.337 4ω2+1.232 3G

(6)

2.6 头水后推求入渗参数的间接法

从土壤入渗模型参数线性预报模型的建立过程和各种显著性分析可以看出，对备耕头水地入渗参数进行预测时需考虑灌水过程中土壤结构变化。但是，在实际实施灌溉时，可以获取的土壤密度数据为灌溉前的数据，应用于考虑灌水过程中土壤结构变化的预报模型存在一定困难。为解决这一问题，依据回归结果以及样本数据进行近一步研究分析，建立灌溉过程发生前后预测参数间的关系，在实际应用中可根据灌水前不考虑灌水过程中土壤结构变化的土壤密度进行入渗模型参数预测，之后据图1和图2表示的两参数预测值之间的关系推求考虑灌水过程中土壤结构的变化的入渗参数。如前所述，入渗指数K和K′的预测值不受灌水过程中土壤结构变化的影响，其余两个参数对于是否考虑土壤结构变化的预测值有一定差别，图1和图2分别表示两参数预测值之间的关系如下：

α=1.297α′-0.064

(7)

f0=1.104f′0-0.009

(8)

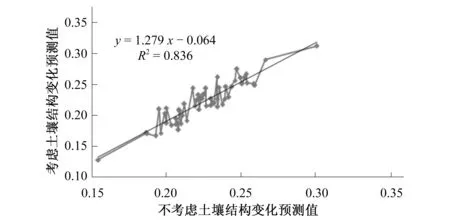
图1 α和α′预测关系

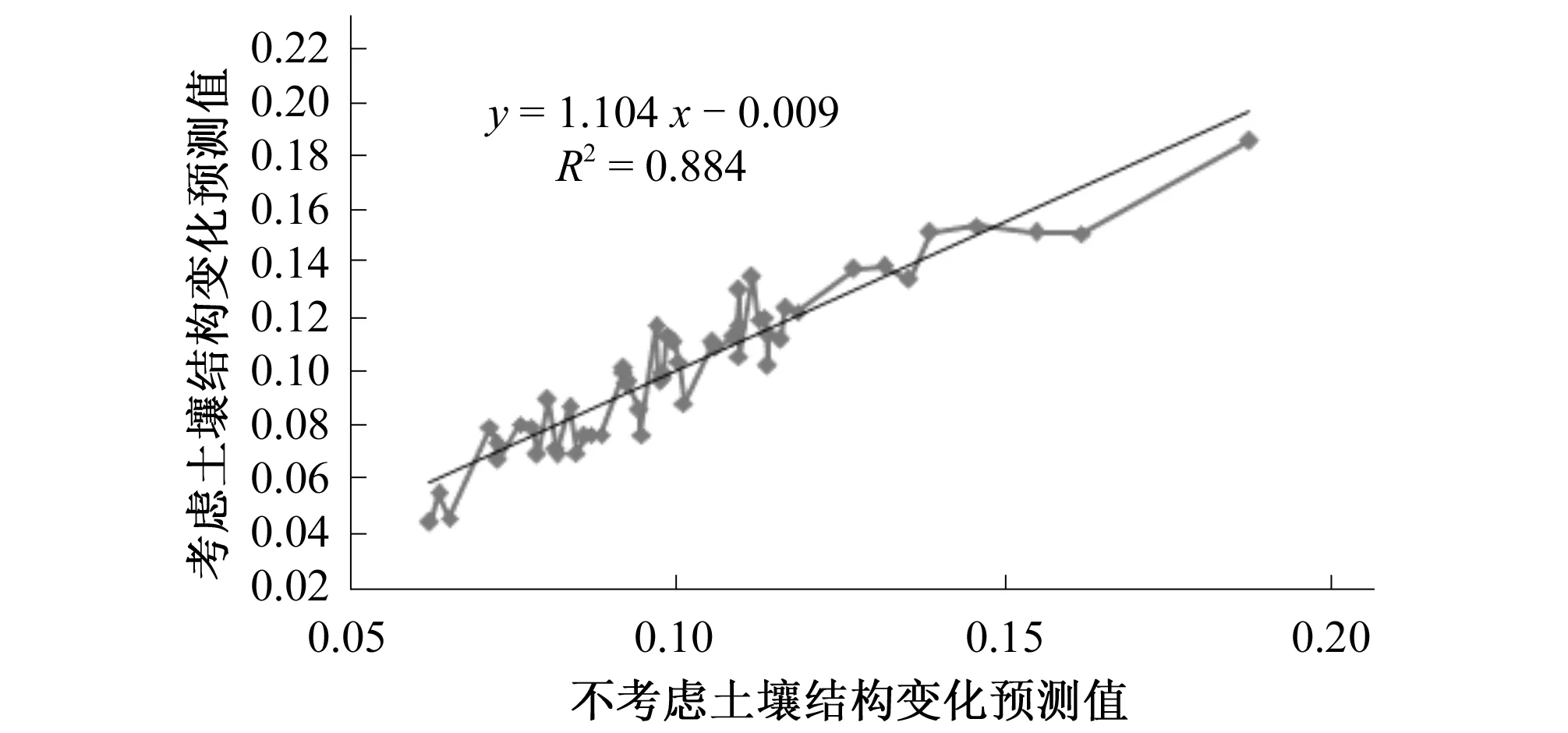
图2 f0和f′0预测关系

3 误差分析

3.1 各参数预报模型平均误差分析

对全部样本数据各参数预报模型的平均误差进行分析，将结果列于表7，由表7可以看出：若考虑土壤结构变化，3个参数预测值的平均误差均较小，控制在15%以下；若不考虑土壤结构变化，除不受土壤结构变化影响的k和k′的平均误差相同外，其余参数预测值的平均误差均高于前者，且f′0的误差较大，高于15%，因此对于头水后土壤入渗能力的预测需考虑土壤结构变化。

表7 各参数预报模型平均误差 %

3.2 预报参数下各入渗模型相对误差分析

为了对入渗模型的预报精度进行分析，将是否考虑土壤结构变化时对应的各参数预报值代入Kostiakov三参数入渗模型，求得在给定时间下入渗率的相对误差进行分析。大田灌溉进行到60 min时土壤水分的入渗过程已基本稳定，大多情况下以90 min时的入渗速率来衡量土壤水分入渗能力[10]。将60组样本数据的预测值分别代入三参数入渗模型求得90 min

时入渗速率的相对误差：不考虑土壤结构变化时相对误差为15.21%，考虑土壤结构变化时相对误差为14.61% ，由此可见考虑土壤结构变化入渗率的相对误差较小，预测值的精度会有所提高，因此对于头水后土壤入渗能力的预测需考虑土壤结构变化。

3.3 头水后入渗参数推求值相对误差分析

利用2.6节所得出的公式间接推求预测参数的相对误差为：α为14.47%；f0为14.86%；将预测参数的推求值代入90 min入渗率公式求得的相对误差为14.89%。将间接法与直接法求得的考虑土壤变形时各参数预测值的相对误差列于表8，可以看出无论是预测参数的相对误差还是给定时间下入渗率的相对误差均大于直接用灌溉后的土壤理化参数计算的预测值相对误差，因此在条件允许的情况下，优先采用考虑直接法进行土壤入渗能力预测。

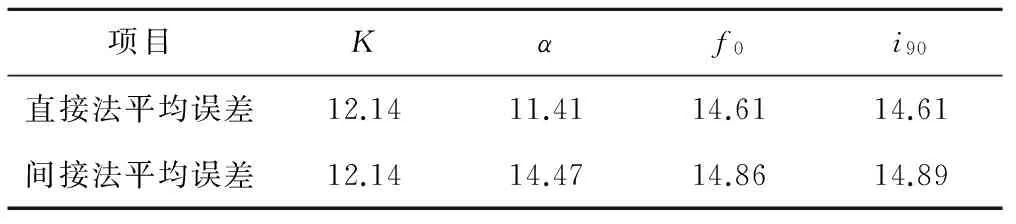
表8 两种方案各参数预报模型平均误差比较 %

3.4 样本外备耕头水地入渗模型预测实例

选取Kostiakov三参数模型对山西省从北到南5个地区运城西渠村、文峪河宋家庄、晋城郎庄村、大同火石沟、吕梁东谊村的土壤水分入渗进行预测，并得到实测入渗量的检验，平均误差范围在0.85%～15.77% 之间，在可接受程度内，能够用于指导当地灌溉。预测方法如下：取预测区土壤进行理化试验，获得各层土壤头水前后密度、体积含水量、不同粒径百分比含量、有机质含量等基本理化指标，将试验获取的各土壤基本理化指标代入本文建立的参数预测模型结构，得到K、α、f0的预测值，将预测值代入三参数入渗模型可得到适用于预测区的土壤入渗模型，利用求得的土壤入渗模型即可得到不同时段的土壤入渗速率，预测实例结果见表9，表10。

表9 考虑土壤结构变形直接预测备耕土壤水分入渗预测实例

表10 不考虑土壤结构变形推求入渗参数间接预测备耕土壤水分入渗预测实例

4 结 语

备耕地灌溉前后土壤地表结构会发生变化(地表土壤密度增加)，为避免灌溉过程中造成的水资源浪费，在生产实践中需考虑这种现象的发生。本文依据可靠性强且代表性好的大田土壤入渗数据及土壤基本理化参数资料建立了是否考虑灌溉后密度增加情况的Kostiakov三参数入渗模型参数的线性预报模型。得到了预测备耕头水地入渗参数的两种方案，经过验证这两种方案均是可行的。采用灌水后增加的土壤密度直接预测模型参数的相对误差较小，均能控制在15%以下。采用直接法困难的情况下，可利用灌水前不考虑土壤结构变化的入渗模型参数预测值，结合灌水过程前后土壤入渗参数预测值的相互关系来推求灌水后土壤结构变形的入渗参数预测值，但是采用此方案无论是从模型各参数的相对误差还是给定时间下入渗率的相对误差来看，均大于直接预测的方法，因此在条件允许的情况下优先考虑直接预测法。

尽管可以用线性回归法建立Kostiakov三参数入渗模型各参数的预报模型进行备耕头水地土壤水分入渗参数预测，但由于各参数与理化性质之间存在非线性关系，本文所建立的线性模型精度还较低，有待进一步进行深入研究，提高预测精度。

□

[1] 雷志栋,杨诗秀,谢森传.土壤水动力学[M].北京:清华大学出版社，1988.

[2] 解文艳,樊贵盛.土壤结构对土壤入渗能力的影响[J].太原理工大学学报,2004,35(4):381-384.

[3] 黄传琴,邵明安.干湿交替过程中土壤胀缩特征的实验研究[J]. 土壤通报,2008,39(6):1243-1247.

[4] 陈 亮,卢 亮.土体干湿循环过程中的体积变形特性研究[J]. 地下空间与工程学报,2013,9(2):229-235.

[5] 樊贵盛,孔令超.土壤脱水过程中结构与含水率间的定量关系[J]. 灌溉排水学报,2012,31(5):40-43.

[6] 曹崇文,樊贵盛.耕作土壤入渗能力衰减机理[J]. 太原理工大学学报,2007,38(2):116-118.

[7] 刘耀宗,张经元.山西土壤[M].北京：科学出版社,1992.

[8] 冯锦萍,樊贵盛.土壤入渗参数的线性传输函数研究[J]．中国农村水利水电.2014,(9):8-11.

[9] 李 卓,刘永红.土壤水分入渗影响机制研究综述[J]. 灌溉排水学报,2011,30(5):124-130.

[10] 樊贵盛,李雪转．非饱和土壤介质水分入渗问题的试验研究[M]．北京：中国水利水电出版社，2012:63-81.

[11] Wosten J H M, Pachepsky Y A, Rawls W J. Pedotransfer functions: bridging the gap between available basic soil data and missing soil hydraulic characteristic [J]. Journal of Hydrology,2001,251:123-150.