基 流 分 割 方 法 研 究——基于辽河流域中下游地区

王远智，梁秀娟，肖长来，尚殿钧，刘洪超(吉林大学地下水资源与环境教育部重点实验室，长春 130021)

基流分割是水文学中研究的一个重点问题，是径流预报，水资源规划管理中的一项重要工作。但是对于基流的研究一直是水文学领域内争论较大的热点之一，原因就在于国内外对于基流的定义存在较大的分歧，径流成分划分不统一，由此造成了分割方法和结果的差异；而且分割方法的不同也使得分割的结果并不完全相同，有时结果差异非常之大。本文采用数字滤波法(Lyne-Holick法、Eckhardt法)和滑动最小值法对辽河流域中下游地区进行地下水基流量分割计算，对计算结果的差异进行分析。

在流域内，地表径流可以通过水文站测得，而基流量却无法测得，因此基流量需要相关的方法进行计算得出。国内外学者对基流量的计算做了很多的工作，国内外通常的基流分割方法包括非线性水库假设法[1]、SWAT模型模拟分割法[2]、HYSEP法[3]、滑动最小值法[4]、Eckhardt滤波法[5]以及数字滤波法[6]等。滑动最小值法以及数字滤波法能够较为快速地分割出基流，使得这两种方法的应用更为广泛。基于此，本文将采用滑动最小值法和数字滤波法对辽河流域中下游地区3个水文站所控断面开展基流分割研究，力求为该地区水资源评价等工作提供一定的参考依据。滑动最小值法由英国水文研究所于1980年提出[4]，Wels等多位学者于1991年编写出了滑动最小值法的计算程序[7]。林学钰等多位学者于2006年在黄河流域地下水资源及其开发利用对策的研究中采用了BFI程序对黄河流域的地下径流量进行了估算[8]。张革等于2013年采用滑动最小值法、数字滤波法和滤波平滑最小值法这3种基流分割方法对香溪河流域进行了研究，结果表明滤波平滑最小值法为这3种方法中最优的基流分割方法[9]。

1 数据来源与方法研究

1.1 数据来源

本文的数据来源取自于辽河中下游地区的水利年鉴，为了能够较为准确的计算出基流量，必须选取无农田灌溉和水利工程的，受人类活动影响小的地区的水文站的实测径流数据，为此选取了辽河流域支流的水库上游的水文站(泉太、王宝庆、八棵树)。为了防止出现水文站数据的偶然性，本文选取了3个水文站进行基流分割。

1.2 滑动最小值法

该方法由英国水文研究所于1980年提出[4]。其基本原理以及计算步骤如下所示。

(1)以Nd为一个计算单元，将连续的日径流量划分为若干个径流量计算单元，需要指出的是N的取值为计算流域的平均汇流时长(d)(本文的3个水文站的平均汇流时间为2 d，因此N=2)。

(2)分别确定在不同时段里的Qmin，并将之记为Q1，Q2，…，Qt。按照顺序，依次分组(Q1，Q2，Q3)，(Q2，Q3，Q4)，…，(Qt-1，Qt，Qt+1)。如果有Qt满足以下条件：

fQt≤min (Qt-1,Qt+1)

(1)

则将该点记做一个拐点，重复上述步骤寻找出所有满足这个公式的点。f(检验因子)的取值前人已经进行了很多的探讨，认为该因子的取值对于基流分割的结果基本没有影响，通常对于f的取值为0.9。

(3)将确定的所有的点连接起来，将所有的拐点见数值用线性插值的方法进行插值。然后将插值所得到的计算值与实际径流量值比较，若计算值大于实际径流值，取实际径流量值作为基流量。这样得到的曲线即为滑动最小值法所分割出来的基流过程线。

1.3 数字滤波法

数字滤波法是世界上应用最为广泛的地下水径流分割方法，这个方法的基本原理就是通过数字滤波器对某一地区的河川径流量等相关数据进行处理，处理后的数据由高频低频组成，其中高频表示的是地下径流量(基流量)，而低频表示的是直接径流量。数字滤波法有多种计算方法，本次计算采用Lyne-Holick滤波法、Eckhardt滤波法进行计算。

(1)Lyne-Holick滤波法是由Lyne和Holick于1979年提出并使用，此后，1990年Nathan和McMahon对这一方法进行了进一步的研究和修正，修正后得到的滤波方程为：

(2)

q=Q-R

(3)

式中：a为滤波参数；Q为河川径流量，m3/s；R为直接径流量，m3/s；q为地下径流量，m3/s；t为时段。

(2)Eckhardt滤波法是由Eckhardt于2005年提出的，其计算公式为：

(4)

式中：BFImax为最大地下径流指数。

根据Eckhardt多年的研究成果，可以得出不同水文地质条件下参数BFImax的经验取值：以孔隙含水层为主的常年河流，BFImax取0.80；以孔隙含水层为主的季节性河流，BFImax取0.50；以弱透水层为主的季节性河流，BFImax取0.25；a一般可以取0.95～0.98。本文所计算流域为常年河流，因此BFImax取0.80，取滤波参数a的取值为0.98。

2 结果与分析

2.1 Lyne-Holick法结果

根据前人的计算结果，本文中滤波参数a取0.925[10],计算结果如表1和表2所示。

表1 Lyne-Holick法基流分割方法(年际)

表2 Lyne-Holick法基流分割结果

从图1中可以看出，本方法分割出的基流量随着径流的增加而增加，而且没有出现随着径流的增加而猛然增加的情况，这一结果比较合理，说明该方法较为适用。而地下径流指数的总体变化规律也正好是丰水年的地下径流指数较小，枯水年较大，除个别年份的数据会出现不同，如2008年的王宝庆水文站的数据：径流量较大，但是地下径流指数也较大，但是从图1(b)中也可以看出，该年的降雨量较为均匀，使得径流的分布也比较均匀，这样也使得基流量所占比例的增加，这一计算结果也较为合理。

图1 Lyne-Holick法基流分割结果

2.2 滑动最小值法结果

使用滑动最小值法计算结果见表3和表4。

表3 滑动最小值法基流分割结果(年际)

从图2可以看出该计算方法也分割出基流，但是从2005年的分割结果来看，其基流量随着径流量的增加出现陡升陡降的情况，这一现象较不合理，因此该方法不能较为准确的计算出该地区的基流量。

2.3 Eckhardt法结果

采用Eckhardt法计算所得的计算结果如表5和表6所示。

从图3可以看出，该计算方法分割出来的基流过程线会随着径流量的增加而增加，并且没有出现陡升陡降的现象，其过程线较为平缓，较为合理，而且本方法也出现和Lyne-Holick方法一样的趋势：个别年份径流量较大，其地下径流指数也较大，而出现这一现象的原因也一样。

表4 滑动最小值法基流分割结果

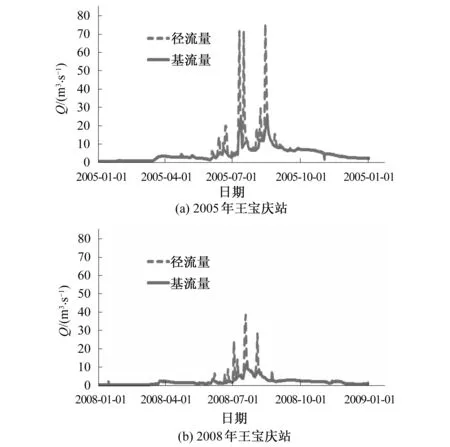
图2 滑动最小值法基流分割结果

表5 Eckhardt法基流分割结果(年际)

表6 Eckhardt法基流分割结果

图3 Eckhardt法基流分割结果

综上所述，Lyne-Holick法以及Eckhardt法能够较为准确并迅速的计算出基流量，而滑动最小值法不能较为准确的计算出基流量。

2.4 合理性分析

本文为了防止数据偶然性，本文采用了3个水文站的数据，而为了便于分析，本文将3个水文站的数据进行了综合处理，将3个水文站的数据进行了总结(3个水文站的经流量以及分割出来的基流量进行求和，再求出基流量所占比例)。

从表7和表8可以看出，枯水时期的地下径流指数较大这一计算结果较为合理，而从计算方法得出的结果的方差也可以看出，滑动最小值法的方差较大，其计算结果年际变化较大，其余两种方法变化较小。这一点也显示出Lyne-Holick法以及Eckhardt法的计算较为合理。

表7 BFI值计算结果(年际)

表8 BFI计算结果

2.5 基流量结果

经过上述分析，Lyne-Holick法以及Eckhardt法的基流量计算结果较为合理，采用两种方法对3个水文站的基流量进行计算，结果见表9和表10。

表9 年际基流量计算结果(Lyne-Holick法、Eckhardt法平均值) 万m3

从计算结果可以得出几个基本数据：①泉太站：年最大基流量约为2.44亿m3，年最小基流量约为0.44亿m3，年平均径流量约为1.34亿m3。②王宝庆站：年最大基流量约为1.31亿m3，年最小基流量约为0.24亿m3，年平均径流量约为0.63亿m3。③八棵树站：年最大基流量约为2.41 亿m3，年最小基流量约为1.22亿m3，年平均径流量约为1.77 亿m3。④各站的基流量主要集中在7-9月。

表10 基流量计算结果(Lyne-Holick法、Eckhardt法平均值) 万m3

3 结 语

(1)本文的3种计算方法中滑动最小值法不能较为准确的反映地下水径流的变化规律，Lyne-Holick法以及Eckhardt法能够较为准确的反映这一变化规律。

(2)地下径流指数的总体变化趋势是径流量较大的年份其地下径流指数一般较小。

(3)本文的计算过程中也发现了一个问题，为了能够较为准确地计算出基流量，必须要有计算时段的前一段时期的径流量数据，从公式中可以看出，基流分割是依据前一时段的径流量对后一时段的影响进行基流分割计算。

(4)辽河流域中下游地区的地下径流指数BFI约为0.59，其中枯水期BFI约为0.63，丰水期约为0.55。

[1] Wittenberg H. Baseflow recession and recharge as nonlinear storage processes [J]. Hydrological Processes, 1999,13(5):715-726.

[2] Neitsch S, Arnold J, Kiniry J, et al. Soil and water assessment tool theoretical documentation, version 2000[M]. Texas, USA: Texas Water Resources Institute, 2005.

[3] Sloto R A, Crouse M Y. HYSEP: a computer program for streamflow hydrograph separation and analysis[R]. US Geological Survey Water-Resources Investigations Report, 1996.

[4] Rutledge A. Computer programs for describing the recession of ground-water discharge and for estimating mean ground-water recharge and discharge from streamflow records[R]. US Geological Survey Water-resources Investigations Report, 1993.

[5] Eckhardt K. How to construct recursive digital filters for baseflow separation [J]. Hydrological Processes, 2005,19(2):507-515.

[6] Lyne V, Holick M. Stochastic time-variable rainfall-runoff modelling[C]∥ Institute Engineers Australia National Conference. Camberra: Institution of Engineers, Australia, 1979,10:89-93.

[7] Wels C, Cornett R J, Lazerte B D. Hydrograph separation: a comparison of geochemical and isotopic tracers [J]. Journal of Hydrology, 1991,122(1):253-274.

[8] 林学钰, 廖资生, 苏小四,等. 黄河流域地下水资源及其开发利用对策[J]. 吉林大学学报(地球科学版), 2006,36(5):677-684.

[9] 张 革, 刘德富, 宋林旭,等. 不同基流分割方法在香溪河流域的应用对比研究[J]. 长江流域资源与环境, 2013,22(2):164-171.

[10] 林凯荣, 陈晓宏, 江 涛,等. 数字滤波进行基流分割的应用研究[J]. 水力发电, 2008,34(6):28-30.