基于压缩感知理论的WSNs时序信号分段压缩算法*

刘洲洲，徐继良，韩　莹，王晓柱（.西安航空学院，西安70077；.空军西安飞行学院第五训练旅，四川南充6700；.中国电子进出口总公司，北京0006）



基于压缩感知理论的WSNs时序信号分段压缩算法*

刘洲洲1，徐继良2，韩莹3，王晓柱1
（1.西安航空学院，西安710077；2.空军西安飞行学院第五训练旅，四川南充637100；3.中国电子进出口总公司，北京100036）

摘要：针对压缩感知理论（CS）应用在无线传感器网络中时序信号在传输过程存在压缩比率低、通信能耗高等问题，提出了一种时序信号分段压缩算法来解决在信号稀疏度未知及高稀疏度条件下，压缩感知数据重构算法中存在的重构效率低，重构精度差，影响网络生命周期的问题。该算法将采集数据中非零元素个数作为分段依据，通过减少段内非零元素组合数量来提高信号重构精度，同时利用了压缩感知理论特性实现了对信号的高压缩率。实验结果表明，在以混沌量子免疫克隆重构（Q-CSDR）算法为重构算法、在信号盲稀疏度及稀疏度高于40的条件下，能够以大于0.4的压缩比率对信号进行压缩，其重构信号的均方误差小于0.01，能够延长网络寿命2倍左右。

关键词：无线传感器网络；压缩感知理论；时序信号；稀疏度；压缩比率

时序信号即为普通时域内的信号，其幅值按照时间先后顺序依次排列。受能量所限，无线传感器网络通常采集和传输的信号以时序信号为主，如何对时序信号进行压缩和高效率传输，是目前无线传感器网络节约通信能耗、延长网络寿命的主要研究方向。

目前，无线传感器网络领域中已有较多的压缩算法，分布式小波压缩算法［1- 2］DWC（Distributed Wavelet Compression）将图像压缩方式引入数据压缩算法中并进行了一定的改动。DWC算法具有压缩性能好，压缩误差小等优点，但其缺点在于算法复杂度高、计算能耗代价大，且奇偶节点之间的大量通信会造成无线传感器节点计算能耗过大而缩短网络寿命。分段线性化压缩算法［3-4］SDT（Swing⁃ing Door Trending）具有算法简单、计算能耗低、计算速度快的优点，能够很好的应用于无线传感器网络节点工作，但分段线性化压缩算法的缺点在于压缩比较小。利用各数据点间的线性关系进行分段数据压缩的SDT算法在传统文物监测系统中性能较好的原因是因为数据变化幅度较小、变化速度较慢。而在信号幅度变化大、变化速率快的文物入侵侦测过程中分段线性化压缩算法的性能受到很大影响。

压缩感知理论［5-7］是近几年来数据和信号处理的研究热点之一，目前在无线传感器网络中得到了广泛的应用。压缩感知理论突破了奈奎斯特采样定理及香农理论的限制性，能够以远小于经典采样方法获取的数据量回复出高质量的原始信号。数据重构算法是压缩感知过程中一个重要的环节，其关键问题在于如何从已知的低维数据中最大程度的恢复出高维数据。目前已有的压缩感知数据重构算法包括梯度投影算法［］、正交匹配算法［］、正则化正交匹配算法［10］、基追踪法［］和基于混沌量子免疫克隆算法的数据重构算法Q-CSDR［］。

当前的数据重构算法在信号具有低稀疏度条件下均有较好的重构性能，而对于高稀疏度和稀疏度无法预估计的信号则会出现重构精度差、算法性能陡然下降等问题。针对以上问题，笔者在分析了压缩感知数据重构算法的基础上，提出了基于压缩感知理论的时序信号分段压缩算法CS-TSSC（Tim⁃ing Signal Subsection Compression）。该算法具有分段方法简单、压缩算法复杂度低等优点，能够明显提高盲稀疏度及高稀疏度条件下信号的重构精度。

1　问题分析

利用线性测量获得的稀疏数据对原始信息进行重建，并在可能的条件下尽可能的保证重建精度，是压缩感知框架中最为关键的操作之一。原始信号的重构过程可以通过求解式（1）的逆问题可以得到，然后通过式（1）获取原始信号X的重构信号：

现有的重构方法总体分为3类：

1.1l22范数最小化重构

l2范数实际上就是最小二乘方案，是最经典的数据重构方式，用l2范数方法表示如式（2）所示：

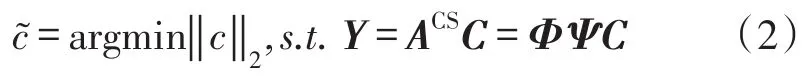
其中对于向量X，其lp范数定义为式（3）：

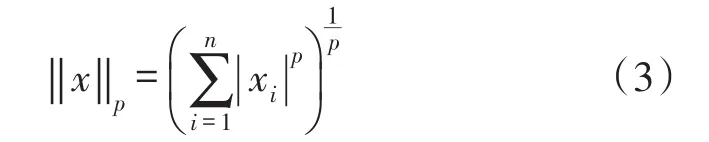
l2范数的最小化重构能够便捷的取得解析解，其形式见式（4）：

这种方法从理论上来讲仅涉及到违逆矩阵乘法等理论，十分简便，但在计算过程中无法获得稀疏解，得到的解析解具有较多的非零元素。因此这种方法实用性并不高。

1.2l0范数最小化重构

l0范数解决了l2范数最小化问题中的解析解非零元素过多的问题，在求解欠定线性方程组的时候，最小化解中的非零元素个数。l0范数与常规范数不同，其值为向量中的非零元素的个数，例如，对于n-稀疏的信号c，其l0范数为n。因此l2范数的最优化问题转化为式（5）：

在实际重建过程中，一般会允许一定的误差存在，因此式（5）也可以表示为式（6）：

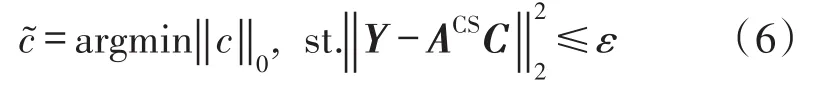
式中，ε为极小常量值。这类问题的求解，都是数值不稳定的NP-完全问题，求解时需要穷举稀疏向量c中的非零元素位置的种可能的组合。

1.3l1范数最小化重构

Candes等人指出，满足M≥nlog2(N/n+1)条件的前提下，利用独立同分布的高斯观测矩阵可以将l0范数问题转化为l1范数问题，并利用式（7）精确重构稀疏信号，可以高概率逼近可压缩信号：

上式在应用时也会允许存在一定的误差，求解时使用式（8）：

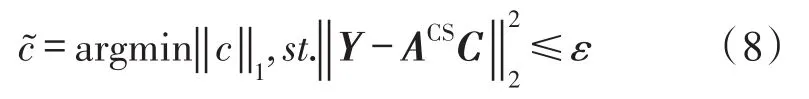
求解l1范数最小化方法将非凸问题转化为凸规划问题，求解过程更简单。寻找最小l1的解空间可以表示为一个线性规划问题。但是使用l1范数进行数据重构存在着计算复杂度高的问题，其计算复杂度为O(N3)。现有的压缩感知数据重构算法大多都是基于以上3种问题而来：其中OMP算法解决的是l0范数问题，其核心内容是以贪婪算法结合迭代方式选取感知矩阵A的列向量，使得被选中的列向量与当前的残差向量具有最大的相关度，然后从观测量中减去相关量，重复这个过程直至达到已知稀疏度n。Q-CSDR算法解决的是l1范数问题，算法本质上仍是一种贪婪算法，其核心内容是利用量子免疫克隆算法的寻优特性，将式（8）作为目标函数，利用量子理论生成随即种群、利用免疫克隆理论实现种群更新，不断地在种群中寻找最优个体。

2　基于压缩感知理论的时序信号分段压缩算法

2.1改进方法

从上述叙述可以看出，基于压缩感知的数据重构算法的本质实际上是在不断生成的种群中寻找原始信号。重构算法的作用在于如何快速准确的寻找出重构数据，其本质上属于NP-hard完全问题。当重构信号的非零元素的位置组合数量过多时，解空间中的解数量巨大，造成了算法的复杂度过高，降低算法寻优效率。下面对信号稀疏度已知以及盲稀疏度两种情况分别进行分析。

在信号稀疏度已知的条件下，假设原始信号X长度为N，其稀疏度为K，其非零元素个数为N×K，则在对X进行重构的过程中需要穷举X中非零元素位置的种可能组合，设其幅值为均匀分布在［min，max］上，则根据概率论相关知识可知，其重建概率为如式（9）：

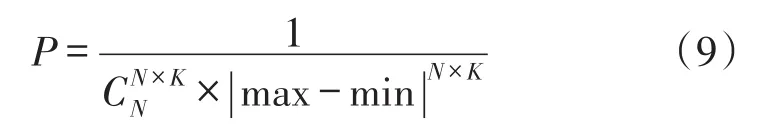
在盲稀疏度条件下，设原始信号X长度为N，则在重构过程中需要对非零元素的分布组合及原始信号的稀疏度同时进行穷举，其排列组合数量为，设其幅值为均匀分布在［min，max］上，则根据概率论相关知识可知，其重建概率为式（10）：

由式（9）、式（10）可以看出，随着原始信号长度N的缩短，重构过程中穷举的组合数量越少，其原始信号的重构概率更高。假设将原始信号划分为n段进行压缩，第i段的长度为Ni，当每段数据中的非零元素数量为K时，则原始信号的重建概率为式（11）：

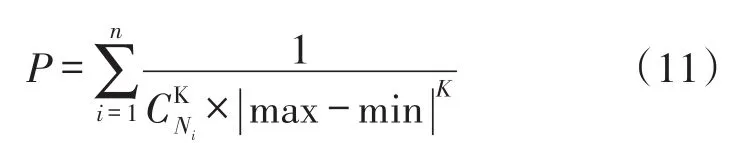
当每段数据中的非零元素数量未知时，则原始信号的重建概率为式（12）：

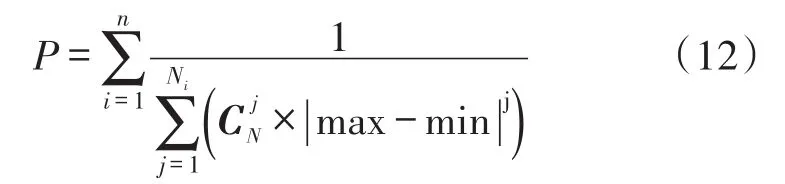
将上述四个公式进行比较，可以看出在同等条件下，分段压缩后的重构概率明显高于分段前的重构概率。而在分段条件下，式（11）的重构概率高于式（12）。由此可以看出，可以通过对原始数据进行分段压缩以提高数据的重构概率，在综合考虑到盲稀疏度及稀疏度已知两种条件下的数据压缩及重构特点，提出了基于压缩感知理论的数据分段压缩算法。

2.2算法步骤

CS-TSSC算法包括两个信号分段及信号数据压缩过程。分段的目的有两个，一是为了减少重构算法穷举数量，提高原始信号的重构概率，二是能够通过分段方法将具有盲稀疏性的信号转化为稀疏度可知的信号，即将求解式（12）的问题转化为求解式（11）的问题。数据压缩过程则是应用压缩感知理论，对每段数据进行分段压缩，实现对时序信号的高比率压缩，以此减少网络通信能耗。

算法步骤如下所述：①参数初始化。包括当前段中非零元素个数temp，当前分段数i、最大分段数量fmax及分段阈值n。②信号分段。从原始信号第一位起，记录当前数据段中非零元素的个数temp，当temp=n时，将其划分为下一数据段的起始数据。将当前段数i加1，n置为0。③若当前分段数seg大于等于最大分段数量fmax时，转入步骤4；否则转回步骤2。④压缩过程。将分段后的原始信号X={x1，x2，…，xfmax}进行分段压缩，以形成压缩后信号Y={Y1，Y2，…，Yfmax}，其中：

Φi为每个分段信号对应的观测矩阵，从观测矩阵字典中查找。由于节点本身的存储空间及运算能力有限，笔者选择了对存储空间要求较小，运算复杂度较低的五种观测矩阵，分别是Hadamard矩阵、稀疏随机矩阵、Toeplitz矩阵、贝努利矩阵和高斯随机矩阵。其中Hadamard矩阵、稀疏随机矩阵和贝努利观测矩阵无法保留原始信号的相应特征，其数据重构概率很低，无法满足系统工作要求。Toeplitz观测矩阵的数据恢复精度及数据恢复概率与高斯随机矩阵相近，但在实验过程中发现Toeplitz观测矩阵通常会出现适应度较差而恢复精度较好的情况，即性能不够稳定，相比之下优先选用高斯随机矩阵均衡性较好。

分段算法举例说明：假设原始信号X为：0 0 0 1 1 1 0 1 0 1 0 1 0 0 1 0 0 0 1 0 1 1 0 1 0 0 1 0 0 0，其原始信号长度为30，当n=2时，可划分成六段数据：0 0 01 1 | 1 0 1 0 | 1 0 1 0 0 | 1 0 0 0 1 0 | 1 1 0 | 1 0 0 1 0 0 0

这种分段方法的特点是除第一段信号外，其余所有数据段的起始位均为非零元素，且无论原始信号的稀疏度是否可预测，其分段后的信号的稀疏度均为已知，因此信号的重构概率大幅提高。表1列举了信号分段前后非零元素位置的组合数量。

表1　分段前后非零元素位置组合数量

从表1的数据可以看出，在信号分段压缩前，数据中非零元素的组合位置数量巨大，特别是在盲稀疏度的条件下，原始信号的组合数量可以达到10 的9次方之多，这也能够解释原始条件下信号重构概率低、重构精度差的原因。同时，从表1中也可以看出，分段压缩后，原始信号的非零元素组合个数数量减少很多，其重构概率大幅提高。

3　实验结果分析

3.1实验参数

实验数据采集自秦始皇兵马俑博物馆K9901号石铠甲展馆旁。节点在其西南方向的树林中呈5×5网状排列，节点与通信基站直接通信组成星状网络。节点采集监测现场的时序信号，在节点处运行CS-TSSC算法后，将数据传输至远程终端服务器使用Q-CSDR算法进行数据重构。在实验中使用三个无线传感器作为信号采集设备对监测区域内的微地震信号进行采集。采集到的信号在节点本地进行滤波、降噪等处理后，再通过分帧和压缩后传输至远端服务器。一个传输未压缩信号，两个传输压缩信号。将三类数据导入计算机，通过MATLAB运行程序对重构的压缩信号进行评估，同时监测3个节点的工作时长。具体实验参数见表2。

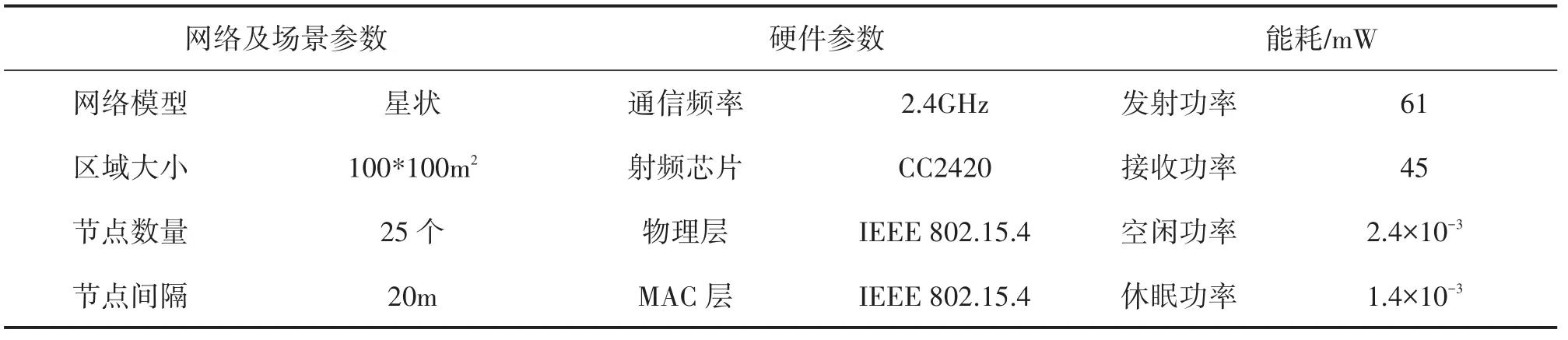
表2　实验参数设置

3.2算法性能结果分析

从图1可以看出，信号的恢复精度实际上受压缩比和数据段内非零元素个数n影响较大，而受数据段长度影响较小。实验结果如图1所示。图中第一行为传感器采集到的原始时序信号，第二行为经压缩感知分段压缩算法压缩后，由Q-CSDR算法逐段恢复并组合成的重构信号，第三行为重构误差，为原始信号与重构信号的差值。

当n=2时，原始数据共分22段数据，信号压缩比为200∶51，近乎达到4∶1。考虑通信中，每个数据包需要额外增加2字节各段数据原长度及稀疏度、总段数、段序列号信息，因此实际数据压缩比率为190∶400=0.475。重建信号的均方误差小于0.01。

如图2所示，当n=3时，原始数据共分15段数据，信号压缩比为200∶59，约为3∶1。考虑通信中，每个数据包需要额外增加2字节各段数据原长度和稀疏度信息，因此实际数据包长度压缩比率为178∶400=0.445。重建信号的均方误差为0.02。

如图3所示，当n=4时，原始数据共分12段数据，信号压缩比为200∶66，约为3.3∶1。考虑通信中，每个数据包需要额外增加2字节各段数据原长度和稀疏度信息，因此实际数据包长度压缩比率为180∶400=0.45。重建信号的均方误差为0.2。

由上述实验结果可以看出，分段阈值n越大恢复精度越低。从传输角度来看n越大分段数越少，产生的通信开销越少，但数据重构概率及精度越差，n越小则重构概率越高、恢复精度越高。

图1　n=2时的数据重构结果

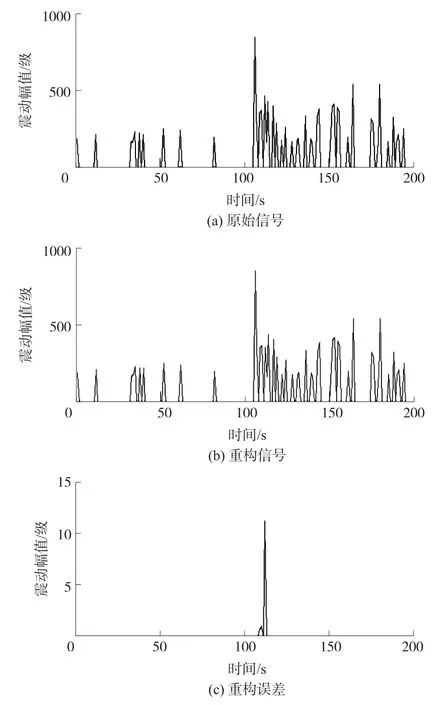
图2　n=3时的数据重构结果

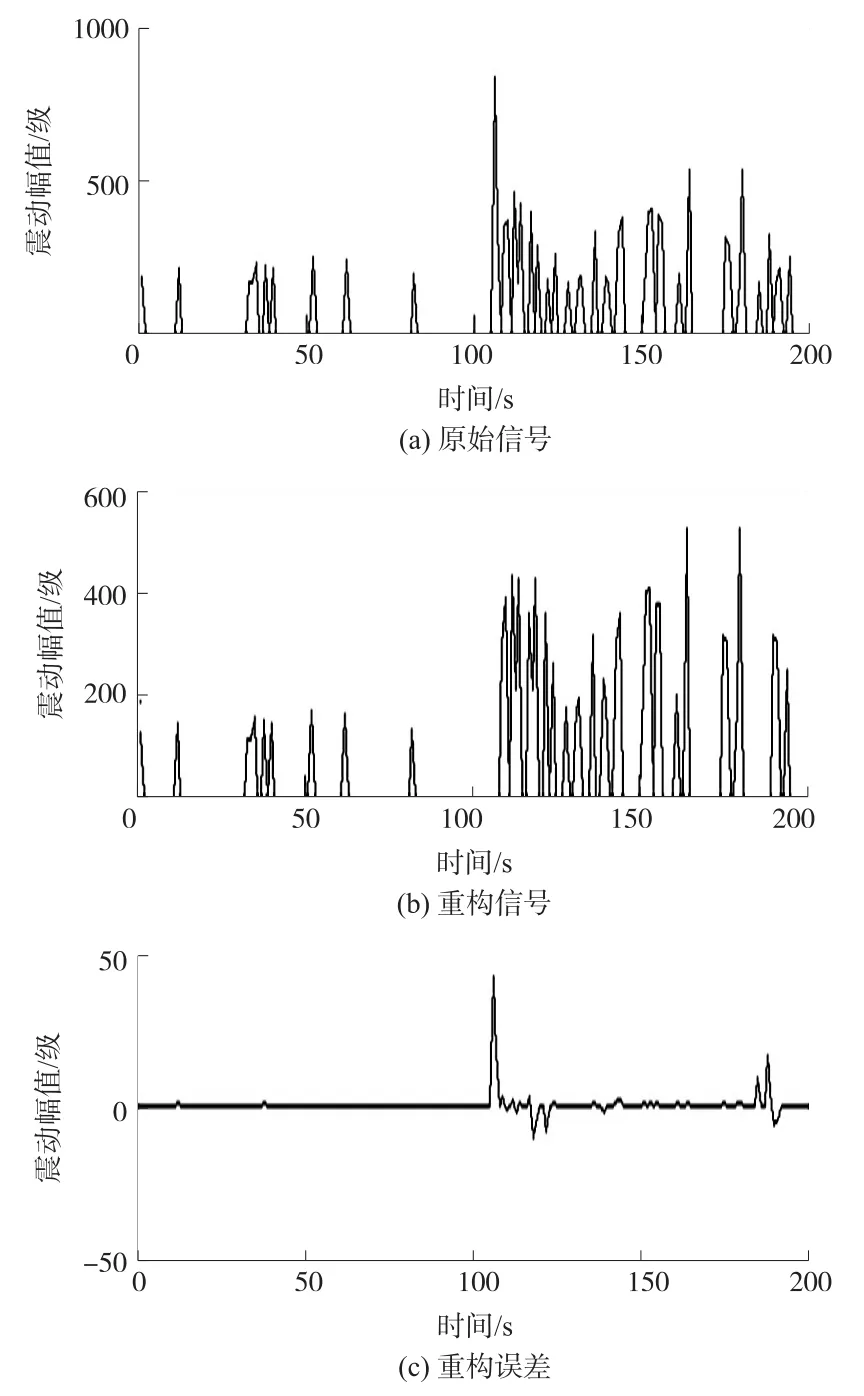
图3　n=4时的数据重构结果

3.3不同稀疏度条件下实验结果分析

笔者针对实验过程中采集的25组长度为200的数据进行压缩和重建，实验结果如图4所示［13］：

可以看出，数据恢复精度在不同稀疏度条件下都比较精确，性能稳定；高稀疏度条件下的精度也较高，但是通信开销和数据压缩比增加了。n=2时的数据恢复精度最好，其压缩比和n=3和n=4时相差不多，其通信开销则高于后两种分帧方式。此外，算法对稀疏度接近45的原始信号仍保持较高的重构概率，减少了估计信号的非零元素排列可能带来的影响。

3.4无线传感器网络数据压缩算法对比

将CS-TSSC与分段线性化压缩的改进算法IS⁃DT的数据恢复性能进行对比。SDT算法是一种直线趋势化压缩算法，算法对于给定的数据限定一个门限值E，并找出最长的直线趋势，通过一条由起点和终点去顶的直线来代替采集的一系列连续数据点。SDT算法现在起点数据垂直距离为门限值E的地方设置两个“支点”。支点与后续的数据之间的连线称为“门”。算法初始化时两扇门均是关闭的。随着更多的数据被采集进入数据序列，这两扇门将根据实际情况进行打开或静止操作，门的宽度是不固定的，且门一旦打开就不能关闭。当这两扇门达到平行时，当前压缩区间结束。将当前数据点的前一个点作为压缩区间的重点，并开始新的一轮压缩。SDT算法性能仅受门限值E影响，而门限值E的选取依赖于经验和实验尝试，且门限值一旦确定后在整个压缩过程中不能改变，因此在信号数据剧烈波动的条件下压缩效果并不理想。ISDT算法针对SDT算法的缺点进行了改进。ISDT算法能够根据数据的波动情况实时、自适应、连续的在一个区间内调整其大小，使算法在压缩过程中始终保持一种较好的压缩状态。ISDT算法根据某个数据点与其前后两个数据点的差值之比作为判断数据波动的依据，不断根据公式对门限值E进行更新。

从上述描述可以看出，ISDT算法虽然压缩性能较好，但是其压缩过程是与数据采集过程紧密关系的，算法不仅要对门限值进行计算，还需要对门限值调整进行计算。这两种算法对于数据幅度波动较小的条件下压缩效果较好，但在数据波动剧烈的条件下数据的压缩效果并不好，且由于门限值需要实时更新的缘故，其计算代价反而会增加。具体对比实验结果如图5所示。

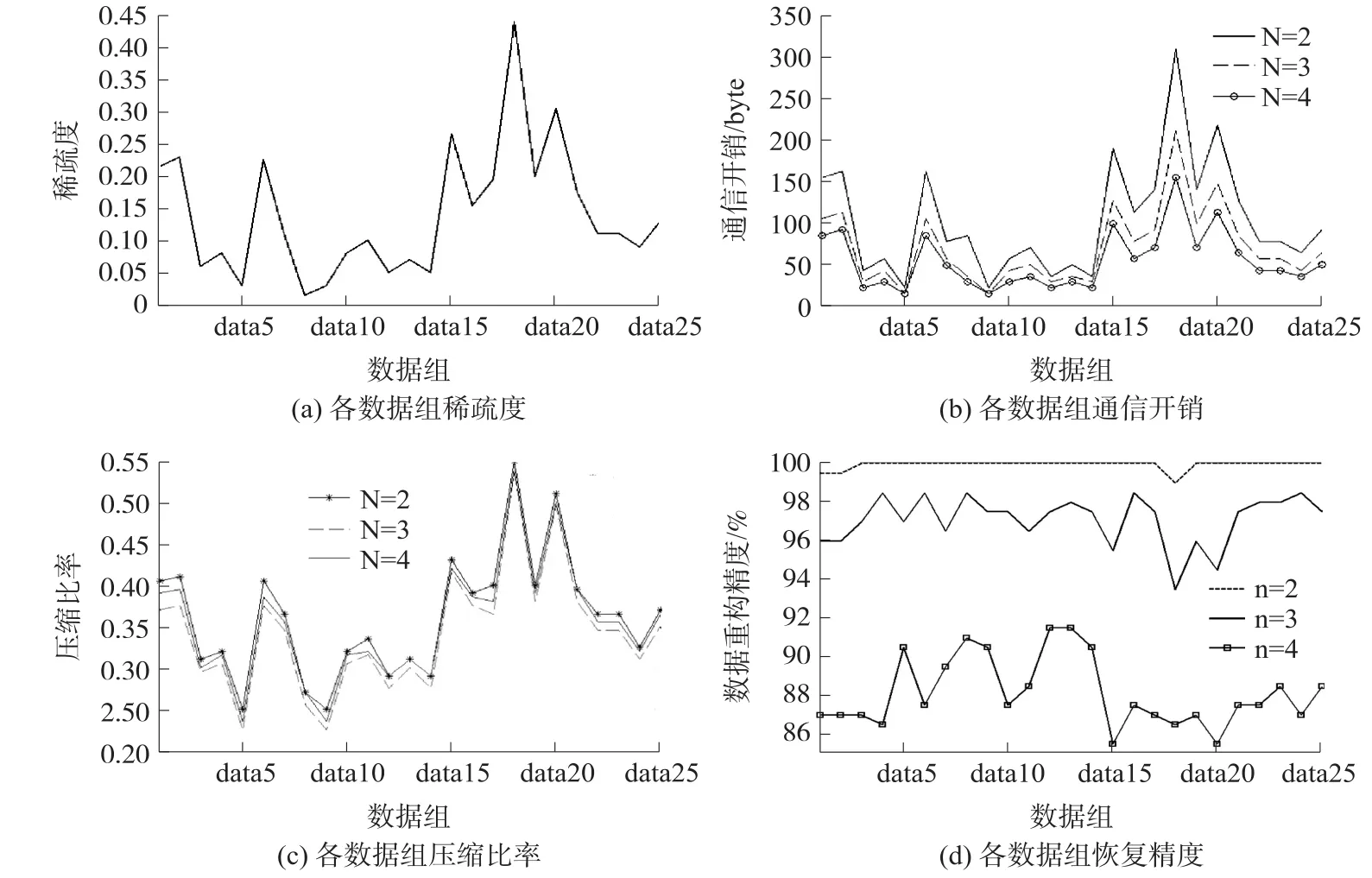
图4　不同稀疏度条件下的试验结果

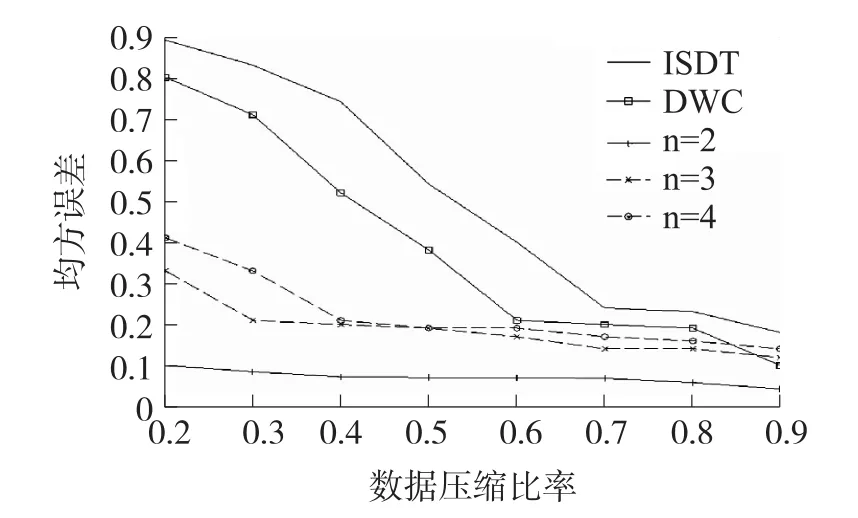
图5　算法性能比较

可以看出，CS-TSSC算法的性能优于对比算法算法，在各种压缩比率条件下均能保持较为稳定的均方误差值，这是因为使用算法后信号重构概率被提高的原因。n=3及n=4时算法在压缩比率大于0.8的条件下性能反而不如ISDT算法。这是由于数据重构算法特性影响的，量子克隆免疫算法在寻优过程中容易陷入局部最优解的原因。同时当压缩比率小于0.2时，CS-TSSC算法的性能也会急剧下降，这主要是因为在数据压缩过程中数据原始信息丢失过多造成的。总体来看，压缩比率在0.2~0.8之间时，CS-TSSC的性能优于其他两类算法。

通过算法叙述及分段方式描述可以看出，分段压缩算法仅针对时间序列信号有较好的效果，而对于图像信号重构则效果很差，其原因是因为图像信号数据量大，分段过多会影响到算法运算速度，降低算法实用性、导致重构算法性急剧降低。因此CSTSSC算法的缺点在于仅能适用于二维序列信号。

4　结论

将压缩感知理论应用于无线传感器网络应用以降低网络及节点通信能耗，延长网络寿命。在分析了压缩感知数据重构原理的基础上，提出了基于压缩感知理论的时序信号分段压缩算法CS-TSSC。该算法能够克服压缩感知理论在数据盲稀疏度及高稀疏度条件下重构精度不高的问题，明显提高了数据重构概率。实验结果表明，相对于现有的经典压缩算法，基于压缩感知理论的数据压缩方法具有计算复杂度低、计算代价小，压缩比率高等特点。但是算法的缺点在于目前仅适用于二维序列信号，因此一些针对数据量大情况下的问题还需要进一步深入研究。

参考文献：

［1］Rein S，Reisslein M. Performance Evaluation of the Fractional Wavelet Filter：A Low-Memory Image Wavelet Transform for Mul⁃timedia Sensor Networks［J］. IEEE Communications Survey & Tu⁃torials，2010，13（2）：291-306.

［2］Luo W H，Wang J L. Based on Hear Wavelet Adaptive Data Com⁃pression Method［J］. Computer Engineering，2010，36（16）：74-76.

［3］Bristol E H. Swinging Door Trending：Adaptive Trending Record⁃ing［C］//National Conference Proceeding. Sydney：ISA 1990：749-753.

［4］王举，房鼎益，陈晓江，等.文物监测中无线传感器网络数据压缩算法［J］.西安电子科技大学学报（自然科学版），2012，39 （1）：157-162.

［5］叶新荣，朱卫平，张爱清，等. OFDM系统选择性慢衰落信道的压缩感知估计［J］.电子与信息学报，2015，37（1）：169-174.

［6］郑仕链，杨小牛.用于调制宽带转换器压缩频谱感知的重构失败判定方法［J］.电子与信息学报，2015，37（1）：236-240.

［7］刘洲洲，王福豹.基于离散萤火虫压缩感知重构的无线传感器网络多目标定位［J］.光学精密工程，2014，22（7）：1904-1911.

［8］Figueiredo M，Nowak R，and Wright S. Gradient Projection for Sparse Reconstruction：Application to Compressed Sensing and Other Inverse Problems［J］. IEEE Journal of Selected Topics in Signal Processing，2007，1（4）：586-597.

［9］轩春青，轩志伟，陈保立.基于最小二乘与粒子群算法的压力传感器动态补偿方法［J］.传感技术学报，2014，27（10）：1363-1367.

［10］高伟，赵博，周广涛.基于带约束人工蜂群算法和平均Haus⁃dorff距离的重力匹配方法［J］.传感技术学报，2014，27（1）：74-78.

［11］Needell D，Tropp J A. CoSaMP：Iterative Signal Recovery from In⁃complete and Inaccurate Samples［J］. ACM Technical Report 2008-01，California Institute of Technology，Pasadena，2008（7）：93-100.

［12］王娟，李飞.一种基于实数编码的量子克隆免疫算法［J］.计算机工程，2012，38（18）：133-136.

［13］祁浩，刘洲洲.基于量子免疫克隆的压缩感知数据重构算法［J］.微处理机，2014，35（5）：34-39.

刘洲洲（1981-），男，山西运城人，博士研究生，讲师，2004、2007年于西北工业大学获得学士、硕士学位，主要从事无线传感器网络方面的研究，liuzhou⁃zhou8192@126.com。

Multidimensional Scaling Localization Algorithm Based on the Shortest Path Matrix Correction

REN Keqiang*，ZHUANG Fangwang
（School of Information Engineering，Jiangxi University of Science and Technology，Ganzhou Jiangxi 341000，China）

Abstract：In order to reduce the difference between the shortest path distance matrix and Euclidean distance ma⁃trix，an improved algorithm of multidimensional scaling node localization was proposed to enhance the node localiza⁃tion accuracy of MDS-MAP（C）algorithm. The algorithm made some improvements on MDS-MAP（C）algorithm. The shortest path distance matrix was corrected by using heuristic search strategy，so as to reduce the error between the shortest path distance matrix and the actual Euclidean distance matrix. Then smacof algorithm iterative error func⁃tion instead of singular value decomposition（SVD）was utilized to solve the problem of node localization，which could optimize and improve the solving process of node localization. The experimental results show that compared with MDS-MAP（C）algorithm，the improved algorithm can reduce the error of the shortest path distance，effectively improve the node localization accuracy，and it has better adaptability to the irregular network.

Key words：wireless sensor network；the shortest path；MDS-MAP（C）algorithm；node localization；multidimension⁃al scaling；smacof algorithm

doi：EEACC：6150P10.3969/j.issn.1004-1699.2016.01.022

收稿日期：2015-03-30修改日期：2015-10-21

中图分类号：TP393

文献标识码：A

文章编号：1004-1699（2016）01-0122-07

项目来源：国家自然科学基金项目（61103242，61401499）