基于网络编码的无线网络容量分析*

孟利民，张　静，周　凯，应颂翔（浙江工业大学信息工程学院，杭州310023）



基于网络编码的无线网络容量分析*

孟利民*，张静，周凯，应颂翔
（浙江工业大学信息工程学院，杭州310023）

摘要：无线网络容量一直是无线网络领域的研究热点，而网络编码通过赋予中间节点对接收数据包进行编码、组合的能力，可以有效提高网络容量，达到最大流—最小割定理确定的理论上限。本文在Gupta和Kumar提出的信号干扰噪声比模型基础上，首先分析网络节点均匀分布时发送节点与目的节点进行多跳传输的无线网络容量计算方法；接着推导出了基于网络编码的无线网络容量计算公式，并利用MATLAB中求解线性规划问题的函数linprog（）求解网络最大流及各链路流量，以此求出无线网络容量上界。通过对无线网络容量上界进行MATLAB仿真，得到如下结论：无线网络容量上界随节点数量的增加呈现先增加后减少的趋势；且当节点数量趋于无穷大时，网络容量趋于零；与传统的存储转发模式相比，采用网络编码有利于提高网络容量。

关键词：无线网络；网络容量；网络编码；最大流—最小割定理

网络容量作为评估无线通信网络性能的重要参数可指导无线网络的优化设计，一直是研究的热点领域。传统无线通信的容量研究主要建立在特定点对点信道下，寻求达到最佳理论性能界限或信道容量。基于点对点通信的香农定理在无线蜂窝通信系统中的应用获得了巨大的成功，但这种方法的主要缺点在于大部分研究成果都只局限于一些简单的网络，而难以进行推广。2000年，Gupta和Kumar［1］等人针对自组织（Ad Hoc）无线网络下的网络容量进行分析，建立了独立同分布下静态节点的无线Ad-hoc网络模型，明确了无线网络容量的定义，提出了著名的无线网络容量计算公式，拉开了无线网络容量研究的序幕。

在Gupta网络容量模型基础上，许多专家提出各种不同的网络容量定义及相应的网络容量计算方法［2-5］。郭中华［6］提出基于欧氏最小生成树的方法，推导了无线网络单播、多播容量理论值。胡晗［7］依据随机几何理论及泊松过程建立了无线网络模型，基于不同的调制方式和纠错编码方案，分析了无线网络的中断概率和网络容量。Rezagah［8］基于信噪比的累积分布函数提出了一种网络容量计算方法并推导出其容量的闭合表达式。在Gupta和Kumar从理论上给出无线网络容量所能达到的界限后，许多学者努力寻找提高网络容量的各种方法。文献［9-10］提出利用节点的移动特性提高网络容量的界限，Yi［11］等人讨论了在随机网络中使用智能天线提高网络容量界限。此外，还有学者认为可利用基础设施［12］或者利用超带宽技术［13］提高网络容量，文献［14］则论述了多向转发对网络容量的增益。

另一方面，网络编码最早在1998年由香港中文大学Robert Li和Raymond Yeung提出，它抛弃了传统通信网络中继节点只对接收信息进行存储和转发的思想，赋予网络节点对接收数据包进行组合、编码等一系列的智能化处理能力，从而进一步提升网络容量。Gastpar等采用Gupta提出的网络模型，在仅考虑中继业务通信且网络中只存在一对发送节点与目的节点的情况下推导得出：若采用复合网络编码，则这类网络的容量在节点数目趋近于无穷时近似为Θ(logn)［15］。本文在Gupta无线网络容量计算方法的基础上，将多跳传输和网络编码相结合，提出基于网络编码思想的无线网络容量计算方法。由于采用网络编码采用多跳传输方式，本文首先分析网络信息多跳传输的连通概率及多跳网络容量计算公式；然后分析采用网络编码思想的网络容量计算方法，最后利用MATLAB中求解线性规划问题的函数linprog（）求解网络最大流及各链路流量，以此求出无线网络容量上界。

1　网络模型

2000年，Gupta和Kumar提出了著名的无线网络容量计算方法。本文采用Gupta信号干扰噪声比（SINR）模型，令i、j分别表示发送、接收节点，l表示同一时刻同一信道向j进行信息传输的节点。pi表示节点i的发送功率，d-ijα表示节点i到节点j的信道增益，则节点j处的接收功率为pid-ijα。在任意时刻，若节点j处的信号干扰噪声比满足如下关系，则节点i与j之间能够进行正常的信息传输。

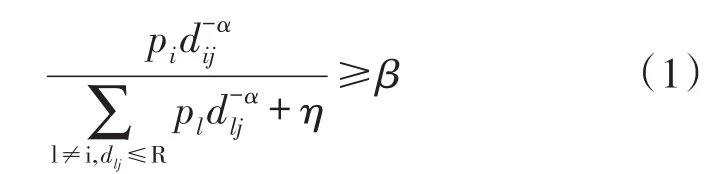
式中，η为环境噪声功率，β为节点成功传输的SINR阈值。

只考虑一个系统中，在中断约束下，无线网络容量表示为单位面积内网络的频谱资源利用率，即链路成功传输概率和网络节点密度乘积。

其中，N表示网络节点总数量，S表示网络总面积，ε表示链路传输的中断概率，即

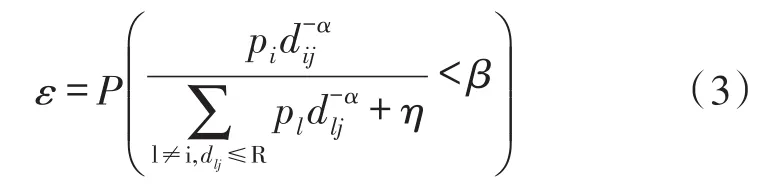
上述无线网络容量计算公式是在分析具有典型意义的单跳链路的基础上得到的。该网络容量公式适用于单跳无线网络，具有一定的局限性。由于采用网络编码采用多跳传输方式，本文首先分析网络信息多跳传输的连通概率及多跳网络容量计算公式。

2　多跳网络容量分析

无线网络中每个节点都有一定的传输半径，当目的节点在发送节点传输范围之内时，两点可直接通信，即通过单跳传输［16］。当目的节点与发送节点之间距离大于传输半径时，则必须通过中间节点进行通信，即通过多跳无线网络通信［17］。

假设节点均匀分布的无线网络面积为S，网络节点总数为N，每个节点都有相同的固定传输半径R。图1表明接收节点在发送节点传输范围之内，即任意两点通过一跳传输的概率表达如下：

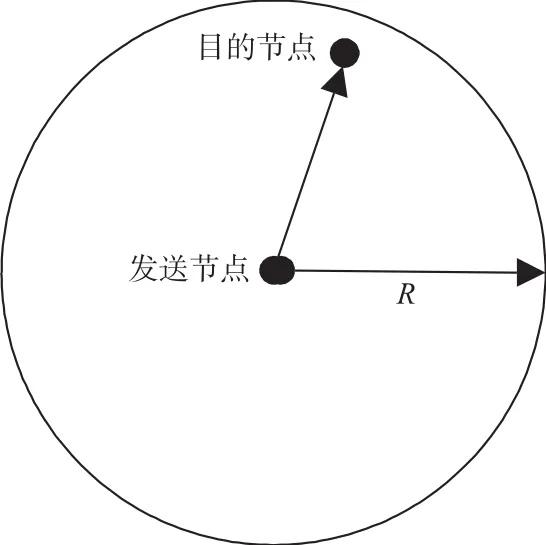
图1　单跳传输网络

当发送节点s与目的节点d之间的距离大于通信半径而小于两倍通信半径时，需要1个中间节点进行转发。即发送节点s与目的节点d通过两跳传输的概率表达如下：

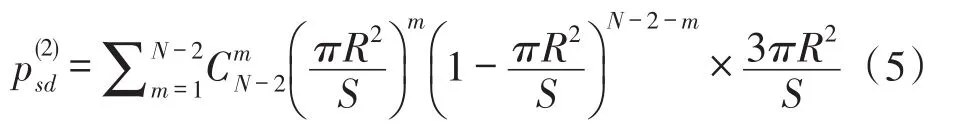
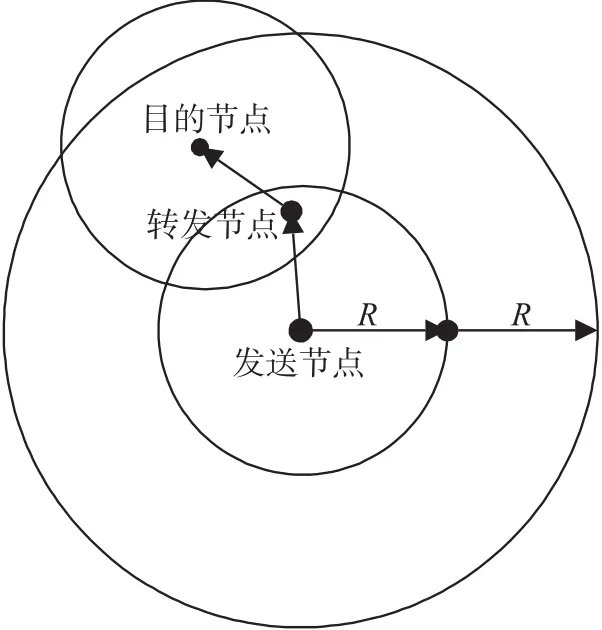
图2　两跳传输网络

同理，当发送节点s与目的节点d之间的距离大于两倍通信半径而小于三倍通信半径时，需要2个中间节点进行转发。即发送节点s与目的节点d通过三跳连通的概率为

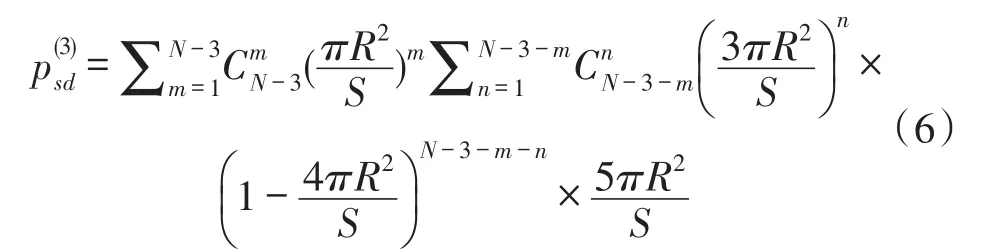
不失一般性，网络四跳连通概率即发送节点s与目的节点d通过三个中间节点转发的概率表达如下：

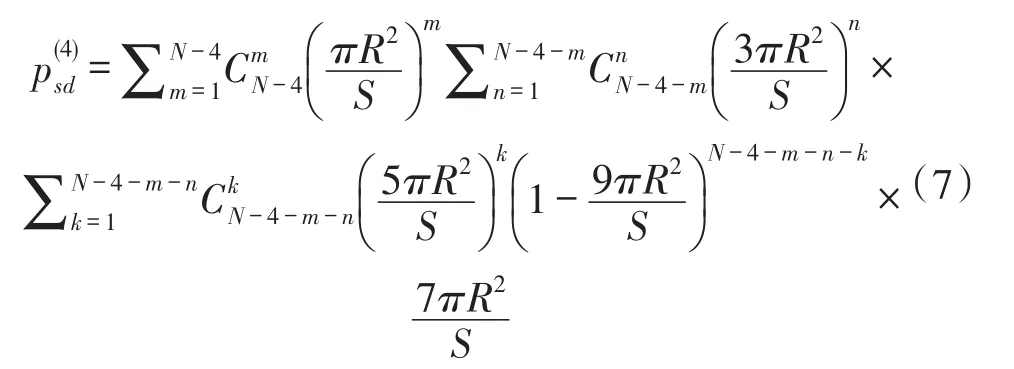
本文对网络节点连通性进行MATLAB仿真。在500 m×500 m的无线网络面积中，节点位置服从均匀分布且传输半径均为80 m。针对不同数量的节点，分别计算网络两跳、三跳、四跳连通概率，如图（3）所示。仿真结果表明：无线网络连通概率随节点数量增加而增加，并逐渐趋于饱和；当节点数量小于10时，两跳连通概率优于三跳、四跳连通概率，而节点数量大于10时，跳数越多，连通性越好。

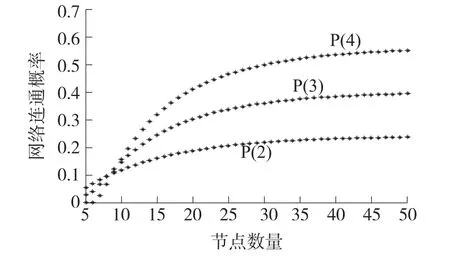
图3　网络连通性与节点数量关系示意图

在多跳网络连通性的基础上，多跳无线网络容量可进一步表示为多跳连通概率、网络成功传输概率和网络节点密度的乘积，即i跳无线网络容量为

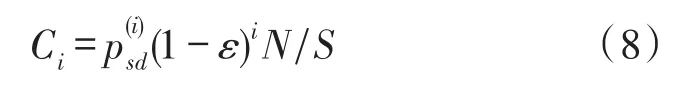
3　基于网络编码的网络容量分析

网络编码是Robert Li等人于1998年提出的一种网络数据传输方式。在传统的路由网络中，网络节点只能对数据进行复制和转发，而在基于网络编码的网络中，网络节点可对接收到的数据进行组合、编码操作，再将结果复制或转发，从而利用网络节点的计算资源来换取带宽利用率，提高网络吞吐量。

Gupta等人提出的网络容量计算方法都是假设端到端传输的信息为单位比特，在引入网络编码后，端到端吞吐量会明显增加，信息传输速率可达到最大流—最小割定理确定的理论上限［18］。如图4所示的蝶形网络，源节点S可以选择两条边不相交的路径S→V1→T1和S→V1→V3→V4→T1传输不同信息到达目的节点T1。同理，源节点S可以选择两条边不相交的路径S→V2→T2和S→V2→V3→V4→T2传输不同信息到达目的节点T2。若采用传统的路由转发策略，则传输链路V3V4为瓶颈链路，不能同时转发两个不同的信息比特。若允许中间节点对接收到的信息进行编码处理，则链路SV1，V1T1，V1V3传输比特 b1，链路SV2，V2T2，V2V3传输比特b2，链路V3V4，V4T1，V4T2传输比特b1⊕b2。则节点T1可收到 b1和 b1⊕b2，通过信息解码，可得到b1和b2。同理，节点T2也可得到b1和b2。

本文在上述无线网络容量计算方法的基础上继续讨论基于网络编码的无线网络容量。当引入网络编码后，发送节点与目的节点的链路流量不能再简单地假设为1。故无线网络容量计算公式可以表达为。其中，c表示发送节点到目的节点传输的信息比特数。

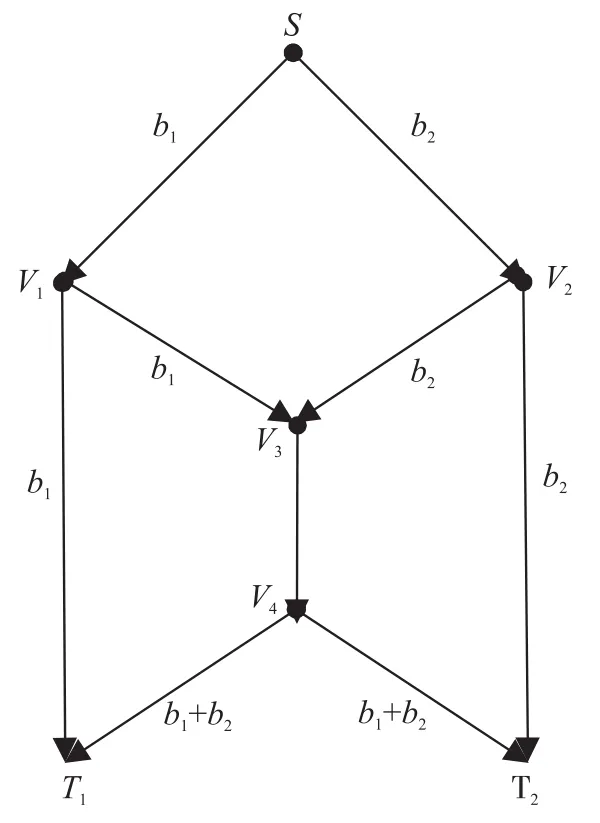
图4　网络编码

由于采用网络编码可以达到最大流—最小割定理确定的理论上限，故我们可以计算发送节点到目的节点的最大流，以及各链路流量，从而得出无线网络容量的上界。

求解网络最大流及各链路流量可以归结为MATLAB中求解线性规划的问题［19］。在MATLAB中求解线性规划问题的函数为linprog（），用于解决以下优化问题：

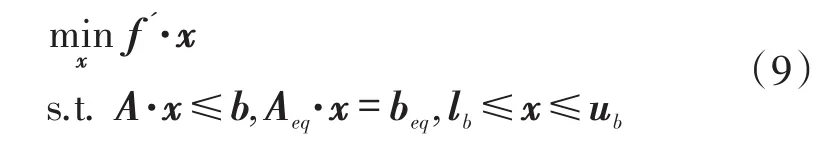
其函数调用格式为[x，fval，exitflag]= linprog(f，A，b，Aeq，beq，lb，ub)：输入参数f为目标函数，以目标函数的系数的列向量形式存在；Α和b为不等式约束条件的数据矩阵；Aeq和beq为等式约束条件的数据矩阵；参数lb和ub为自变量的范围。函数返回的参数x为线性规划的最优解；fval为最优解x处的函数值；exitflag为解的输出标志，当找到最优解时，exitflag=1，当线性规划无解时，exitflag=-1。

如蝶形网络图5所示，各链路xi都有相应的容量，假设各链路流量分别为x1、x2、x3、…、x11，可利用MATLAB中线性规划方法确定从发送节点S到目的节点T的最大流，并求解相应链路的流量值。

由于网络的流入量等于网络的流出量，所以x1+x2=x5+x7+x8+x9。我们需要求解g=x1+x2的最大值，即目标函数f=-x1-x2的最小值。除了发送节点和目的节点，其他中间节点的流入量等于流出量，即

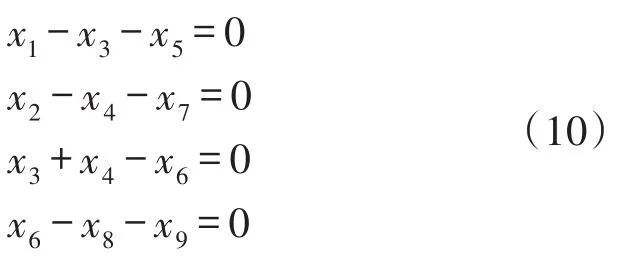
图5　网络图

假设各链路的容量为wi，(i=1，2，L，8，9)，则各链路流量不大于其容量，即

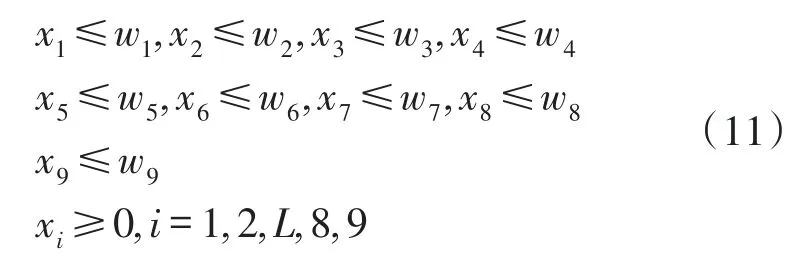
由（10）可得，Aeq·x=beq，其中

由（11）可知，

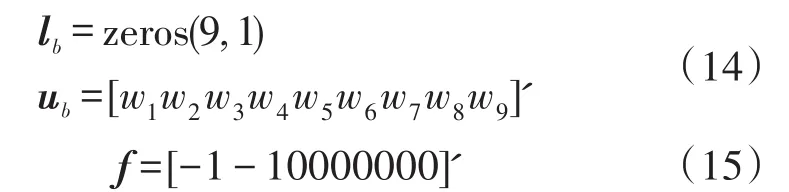
通过MATLAB仿真[x，fval，exitflag]= linprog(f，[ ]，[ ]，Aeq，beq，lb，ub)，得fval=-37.2052，x= ［18.1472 19.0579 3.2895 7.3578 14.8578 10.6473 11.7001 4.3624 6.2849］。即最大值g=37，相应链路流量x1=18.1，x2=19.0，x3=3.2，x4=7.3，x5=14.8，x6= 10.6，x7=11.7，x8=4.3，x9=6.2，如图6所示。

由图6可知，若采用传统的路由转发策略，源节点S可经路径S→V1→T1传输14.8比特信息到目的节点T1，经路径S→V2→T2传输11.7比特到目的节点T2。而采用网络编码方案，源节点S可以选择路径S→V1→T1和S→V1→V3→V4→T1传输14.8+4.3= 19.1比特信息到达目的节点T1，同时源节点S经路径S→V2→T2和S→V2→V3→V4→T2传输11.7+6.2= 17.9比特信息到达目的节点T2。所以，网络容量为。其中，ci、pi、(1-εi)分别为发送节点到目的节点的i条路径中各自的传输信息比特、连通概率和成功传输概率。

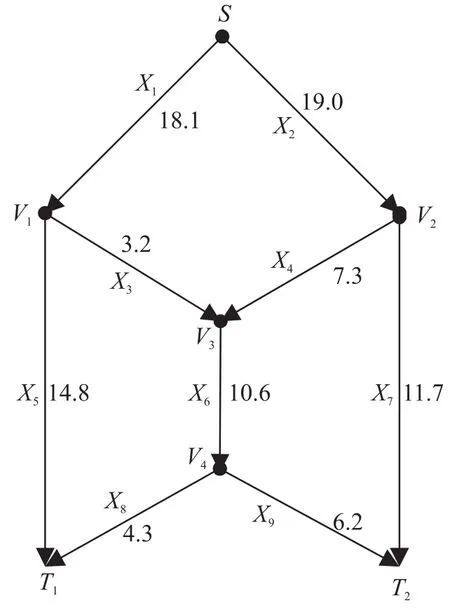
图6　流量网络图

假设信道信噪比阈值为1.3，α=2，信道环境噪声忽略不计。在无线网络面积为500 m×500 m，节点通信半径为80 m和无线网络面积为400 m× 400 m，节点通信半径为60 m两种情况下，我们分别对无线网络容量上限进行仿真，如图7所示。

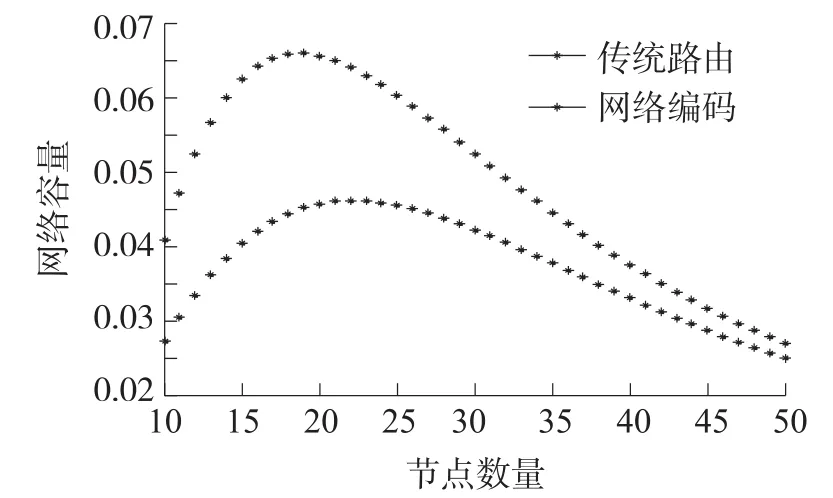
图7　无线网络面积为500 m×500 m，节点通信半径为80 m时网络容量上界仿真图

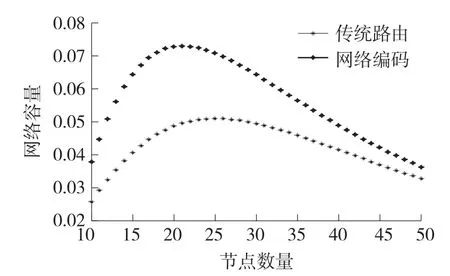
图8　无线网络面积为400 m×400 m，节点通信半径为60 m时网络容量上界仿真图

从图中可以发现：每条曲线都呈现出无线网络容量上界随节点数量的增加呈现先增加后减少的趋势且当节点数量趋于无穷大时，网络容量趋于零，这也与Gupta的结论相一致，即网络中节点数目的增加是以容量的减少为代价；与传统存储转发模式相比，采用网络编码有利于提高无线网络容量。

4　结束语

在Gupta信噪比网络容量模型的基础上，本文提出了一种基于网络编码的无线网络容量计算方法。Gupta信噪比网络容量模型假设发送节点到目的节点的信息传输比特为1，而网络编码会提高端到端的吞吐量，计算发送节点到目的节点的信息传输比特数可以更精确地描述无线网络容量。采用网络编码必会经过多跳传输，本文首先分析了网络的多跳连通性及多跳网络容量计算，随后提出基于网络编码的无线网络容量计算公式，并利用MATLAB中求解线性规划的方法得出利用网络编码可达到的最大流及各链路流量，由此可知发送节点到目的节点的几条路径各自传输的信息比特数，并求出无线网络容量上界。通过仿真发现：无线网络容量上界随节点数量的增加呈现先增加后减少的趋势，且当节点数量趋于无穷大时，网络容量趋于零，即网络中节点数目的增加是以容量的减少为代价；与传统存储转发模式相比，采用网络编码有利于提高无线网络容量。

参考文献：

［1］Gupta Piyush，Kumar P R. The Capacity of Wireless Networks［J］. IEEE Transactions on Information Theory，2000，46(2)：388-404.

［2］Hwang Y J，Seong Lyun Kim. The Capacity of Random Wireless Networks［J］. IEEE Transactions on Wireless Communications，2008，7(12)：4968-4975.

［3］Dousse O，Franceschetti M，Thiran P. On the Throughput Scaling of Wireless Relay Networks［J］. IEEE Transactions on Informa⁃tion Theory，2006，52(6)：2756-761.

［4］周凯，孟利民，华惊宇.基于Grover路由策略的无线传感网络剩余容量构造与研究［J］.传感技术学报，2015，28(2)：249-253.

［5］Kannan S，Viswanath P. Capacity of Multiple Unicast in Wireless Networks：A Polymatroidal Approach［J］. IEEE Transactions on Information Theory，2014，60(10)：6303-6328.

［6］郭中华，史浩山.基于欧式最小生成树的无线Ad Hoc网络容量研究［J］.传感技术学报，2008，21(10)：1750-1754.

［7］胡晗，朱洪波，朱琦.无线Ad hoc网络传输容量的性能分析［J］.电子与信息学报，2012，34(6)：1457-1462.

［8］Rezagah R E，Mohammadi A. Analyzing the Capacity of Wireless Ad Hoc Networks［J］. Telecommunication Systems，2014，55(1)：159-167.

［9］Grossglauser M，Tse D N C. Mobility Increases the Capacity ofAd-Hoc Wireless Networks［J］. IEEE Transaction on Networking，2002，3：1577-1586.

［10］Jae Young Seol，Seong Lyun Kim. Node Mobility and Capacity in Wireless Controllable Ad hoc Networks［J］. Computer Communi⁃cations，2012，35(11)：1345-1354.

［11］Yi S，Pei Y，Kalyanaraman S. On the Capacity Improvement of Ad- Hoc Wireless Networks Using Directional Antennas［C］// ACM MobiHoc 2003. New York，2003. 108-116.

［12］Dousse O，Thiran P，Hasler M. Connectivity in Ad-Hoc and Hy⁃brid Networks［C］// IEEE INFOCOM 2002. 21st Annual Joint Conference of the IEEE Computer and Communications Societies. New York，2002. 1079-1088.

［13］Negi R，Rajeswaran A. Capacity of Power Constrained Ad- Hoc Network［C］// IEEE INFOCOM 2004. 23rd Annual Joint Confer⁃ence of the IEEE Computer and Communications Societies. Hong Kong，2004. 443-453.

［14］Nousiainen J，Virtamo J，Lassila P. Impact of Multidirectional For⁃warding on the Capacity of Large Wireless Networks［J］. IEEE Communications Letters，2014，18(2)：372-375.

［15］Gastpar M，Vetterli M. On the Capacity of Wireless Networks：the Relay Case［C］// IEEE INFOCOM 2002. 21st Annual Joint Con⁃ference of the IEEE Computer and Communications Societies. New York，2002. 1577-1586.

［16］刘少阳，赵海涛，魏急波，等.多跳无线网络中路径端到端容量的准确计算［J］.软件学报，2013，24(1)：164-174.

［17］夏少波，邹建梅，朱晓丽，等.基于跳数区域划分的DV-Hop改进算法［J］.传感技术学报，2014，27(7)：964-969.

［18］樊平毅.网络信息论［M］.北京：清华大学出版社，2009. 126-127.

［19］王薇. MATLAB从基础到精通［M］.北京：电子工业出版社，2012. 363-364.

孟利民（1963-），女，教授，博士生导师，信息与通信工程专业工学博士，浙江工业大学信息与通信系统研究所所长，浙江省光纤通信技术重点实验室主任。主要研究方向为无线通信与网络、多媒体数字通信、网络通信与控制通信信号处理与软件无线电，mlm@zjut.edu.cn；

张静（1989-），女，硕士研究生，就读于浙江工业大学信息工程学院，主要研究方向：无线网络容量计算、网络编码，zjing890921@163.com。

Timing Signal Subsection Compression Algorithm in WSNs Based on Compressed Sensing Theory*

LIUZhouzhou1，XUJiliang2，HAN Yin3，WANGXiaozhu
（1.Xi’an Aeronautical University，Xi’an 710077，China；2.Air Force Xi'an Flight Academy Fifth Training Brigade，Nanchong Sichuan 637100，China；3.Chinese Electronics Import and Export Corporation，Beijing 100036，China）

Abstract：For compressive sensing（CS）application timing signal during transmission in the wireless sensor net⁃works has low compression ratio，high energy consumption of communication，the timing signal segment compres⁃sion algorithms is proposed to solve the unknown signal sparsity and high sparsity under conditions of low compres⁃sive sensing reconstruction efficiency data reconstruction algorithm when the reconstruction accuracy is poor. As the basis of segmentation，the number of non zero elements is collected in the data，by reducing the number of com⁃binations of nonzero elements within the segment to improve the accuracy of signal reconstruction，while taking ad⁃vantage of the characteristics of compressive sensing theory to achieve a high compression ratio of the signal. Experi⁃mental results show that，under the chaotic quantum clonal Reconstruction（Q-CSDR）algorithm as the reconstruc⁃tion algorithm，the blind signal sparsity and sparse conditions is higher than 40，the compression ratio can be great⁃er than 0.4，the signal has been compressed，and square error of less than 0.01 of its reconstructed signal，and the network lifetime is prolonged by about 2 times.

Key words：wireless sensor networks；compressive sensing theory；the timing signal；sparsity；compression ratio

doi：EEACC：7230；7230V10.3969/j.issn.1004-1699.2016.01.021

收稿日期：2015-07-28修改日期：2015-10-05

中图分类号：TP393.0

文献标识码：A

文章编号：1004-1699（2016）01-0116-06

项目来源：国家自然科学基金项目（61372087）